Varianz- und Regressionsanalyse
17 Zweifaktorielle Varianzanalyse (Two-Way ANOVA)
17.0 Einführung Zweifaktorielle Varianzanalyse
Im letzten Kapitel haben Sie die einfaktorielle Varianzanalyse kennengelernt. Diese untersucht, ob es signifikante Unterschiede zwischen den Mittelwerten mehrerer Gruppen gibt, die sich hinsichtlich eines Faktors unterscheiden. Zum Beispiel haben wir im letzten Kapitel untersucht ob sich unterschiedliche Lernmethoden auf die Einarbeitungszeit auswirken. Nehmen wir nun einen weiteren Faktor hinzu und untersuchen beispielsweise, ob sich die Einarbeitungszeit von Mitarbeitenden nicht nur zwischen den Lernmethoden unterscheidet, sondern auch abhängig vom Geschlecht ist verwenden wir die zweifaktorielle Varianzanalyse. Die zweifaktorielle Varianzanalyse untersucht, ob es signifikante Unterschiede zwischen den Mittelwerten mehrerer Gruppen gibt, die sich bezüglich zwei Faktoren unterscheiden. Man kann dieses Beispiel natürlich auch um weitere Faktoren erweitern (z.B. Altersgruppen) und spricht dann von einer dreifaktoriellen oder ganz allgemein von einer mehrfaktoriellen Varianzanalyse. Je mehr Faktoren (unabhängige Variablen) sie betrachten, desto komplexer wird die Interpretation der Ergebnisse. Daher sollten Sie sich möglichst auf den zweifaktoriellen Fall beschränken auf den wir im Folgenden auch näher eingehen.
Um ihnen die Funktionsweise anschaulich darzustellen, führen wir das eben genannte Beispiel fort. Wir möchten herausfinden, welche Lernmethode sich für das Burgerbraten am besten eignet und ob es hierbei Unterschiede zwischen Männern und Frauen gibt (Um das Beispiel nicht zu kompliziert zu machen gehen wir im Folgenden davon aus, dass es nur diese beiden Geschlechter gibt). Um dies herauszufinden, haben wir sechs unabhängige Gruppen gebildet. Drei Gruppen von Frauen, die nach jeweils einer der drei Lernmethoden das Burgerbraten lernen, und drei Gruppen mit männlichen Teilnehmern. Bei allen Gruppen wurde die Dauer der Einarbeitung in Tagen gemessen, die die Teilnehmenden benötigt haben. Desto schneller, desto besser.

Um unsere Fragestellung zu beantworten, führen wir nun im Folgenden eine unabhängige zweifaktorielle Varianzanalyse mit einem sogenannten 3×2 Design durch (da 3 Lernmethoden und 2 Geschlechter).
Expertenwissen: Messwiederholung und ANOVA
In dem eben besprochenen Beispiel sind alle Gruppen voneinander unabhängig (in jedem der 6 Kästen sind andere Menschen). Dies muss nicht immer so sein. Es könnte auch sein, dass zum Beispiel jede Person drei unterschiedliche Lernmethoden durchläuft (vielleicht auch mit zeitlichem Abstand) und jeweils danach die Leistung gemessen wird. Dies nennt man dann ein Messwiederholungsdesign, da die für die selbe Person zu mehreren Zeitpunkten Daten erhoben werden. Hierfür gibt es die sogenannte Messwiederholungs-Varianzanalyse (im englischen repeated measure ANOVA). Kommt dann noch ein zweiter Faktor hinzu, der wiederum unabhängig ist (wie das Geschlecht) benötigt man die gemischte Varianzanalyse (im englischen mixed ANOVA). Beide Spezialfälle werden wir in diesem Grundlagenbuch jedoch nicht weiter vertiefen. Zu welchem Versuchsaufbau sich welche Varianzanalyse eignet, erklärt Ihnen auch nochmal anschaulich das folgende Video.
16.1 Mehrfaktorielle Varianzanalyse | Einführung
17.1 Voraussetzungen
Die Voraussetzungen der zweifaktoriellen Varianzanalyse (ANOVA) sind dieselben, wie schon bei der einfaktoriellen Varianzanalyse aus dem letzten Kapitel. Deshalb werden diese hier nur kurz erläutert:
- intervallskalierte abhängige Variable
- Messwerte sind unabhängig voneinander
Jede unserer Gruppen muss unterschiedliche Probanden aufweisen. Haben wir ein Messwiederholungsdesign, wo dieselben Personen in mehreren zu vergleichenden Gruppen auftreten, führen wir stattdessen eine Varianzanalyse mit Messwiederholung durch. - Normalverteilung der abhängigen Variablen in allen Testgruppen
Überprüfbar über einen Kolmogorov-Smirnov, Lilliefors oder Shapiro-Wilk Test, die für die Annahme der Normalverteilung nicht signifikant werden dürfen. Da die ANOVA jedoch recht robust ist gegenüber Verletzungen dieser Voraussetzungen, kann bei ausreichender Stichprobengröße dies auch vernachlässigt werden. - Varianzhomogenität in allen Gruppen
Überprüfbar über den Levene-Test, der nicht signifikant werden sollte, um Varianzhomogenität (also gleiche Streuung der AV in allen Gruppen) annehmen zu können.
16.4 Mehrfaktorielle Varianzanalyse | Voraussetzungen
17.2 Hypothesen
Im Gegensatz zu den anderen Testverfahren, die Sie bisher kennengelernt haben, untersucht die zweifaktorielle Varianzanalyse nicht nur eine sondern ganze drei Hypothesenpaare. Dies macht auch Sinn, denn wir können mit unserem Versuchsdesign verschiedene Unterschiede zwischen den Gruppen testen.
Zum einen können wir uns die Frage stellen, ob sich die benötigte Einarbeitungszeit ganz generell zwischen den drei Lernmethoden unterscheidet (unabhängig vom Geschlecht). Dies entspricht der Frage, der wir im letzten Kapitel schon nachgegangen sind. Jedoch können wir nun auch herausfinden, ob es generelle Unterschiede zwischen Männern und Frauen in der Dauer der Einarbeitung gibt (unabhängig von der Lernmethode). Die ersten beiden Hypothesenpaare untersuchen also, ob es signifikante Unterschiede zwischen den Faktorstufen eines Faktors gibt, ohne dabei den anderen Faktor zu betrachten. In unserem Beispiel ergeben sich folgende Hypothesen:
H0: Es gibt keinen signifikanten Unterschied in der Einarbeitungsdauer zwischen den drei Lernmethoden.
H1: Es gibt min. 1 signifikanten Unterschied in der Einarbeitungsdauer zwischen den drei Lernmethoden.
H0: Es gibt keinen signifikanten Unterschied in der Einarbeitungsdauer zwischen Männern und Frauen.
H1: Es gibt min. 1 signifikanten Unterschied in der Einarbeitungsdauer zwischen Männern und Frauen.
Die beiden Hypothesenpaare untersuchen die beiden Haupteffekte (was das genau ist, erfahren Sie im nächsten Absatz).
Das dritte Hypothesenpaar betrachtet die Kombination beider Faktoren (Lernmethode und Geschlecht) im Hinblick auf die abhängige Variable. In unserem Beispiel können wir uns fragen, ob die Art der Lernmethode einen anderen Einfluss auf die Dauer der Einarbeitung von Frauen als von Männern hat. Zum Beispiel könnten ja bestimmte Lernmethoden bei Frauen besser funktionieren als bei Männern oder andersherum. Daraus ergibt sich folgendes drittes Hypothesenpaar:
H0: Die Einarbeitungsdauer zwischen Frauen und Männern wird nicht von der Lernmethode beeinflusst. (Die beiden Faktoren sind unabhängig voneinander)
H1: Die Einarbeitungsdauer zwischen Frauen und Männern ist abhängig von der Lernmethode. (Die beiden Faktoren beeinflussen sich gegenseitig).
Damit untersuchen wir eigentlich, ob die beiden Faktoren unabhängig voneinander sind oder sich gegenseitig beeinflussen (z.B. verstärken). Ist dies der Fall (H1 wird angenommen) liegt ein sogenannter Interaktionseffekt vor (dazu mehr im nächsten Absatz).
16.5 Mehrfaktorielle Varianzanalyse | Hypothesen
17.3 Funktionsweise
Wie auch schon bei der einfaktoriellen ANOVA untersucht auch die zweifaktorielle ANOVA, ob die Streuung der Daten in unserer Stichprobe eher auf systematische Einflüsse, wie das Geschlecht oder die Lernmethode, zurückzuführen ist oder, ob sie durch zufällige Unterschiede zwischen den Probanden entsteht. Dazu wird die Gesamtvarianz in die Modellvarianz (systematische Einflüsse durch unsere zwei Faktoren) und die Fehlervarianz aufgeteilt. Die verschiedenen Varianzen werden mithilfe von Quadratsummen betrachtet. (Einen tiefergehenden Einblick, was sich hinter welchem Begriff genau verbirgt, finden sie im letzten Kapitel).
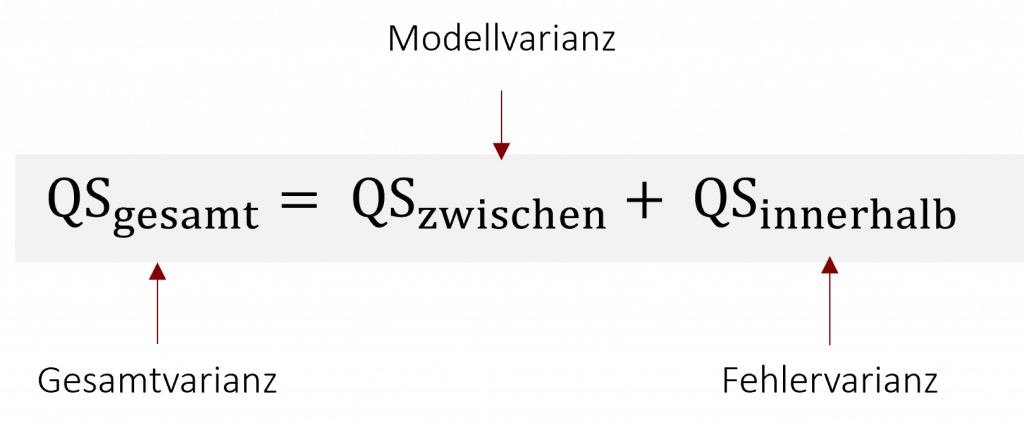
Doch was ist nun der Unterschied zwischen der ein- und der zweifaktoriellen Varianzanalyse? Bei der einfaktoriellen ANOVA können die Unterschiede zwischen den Gruppen (=Modellvarianz) auf nur einen Faktor, beispielweise die verschiedenen Lernmethode, zurückgeführt werden. Bei der zweifaktoriellen ANOVA ist dies nicht mehr so einfach. So können die Unterschiede zwischen den Gruppen in unserem Beispiel aufgrund der unterschiedlichen Lernmethode oder aufgrund des Geschlechts oder durch irgendeine Kombination beider Faktoren entstehen. Aus diesem Grund müssen wir die Modellvarianz auf die verschiedenen Effekte aufteilen.
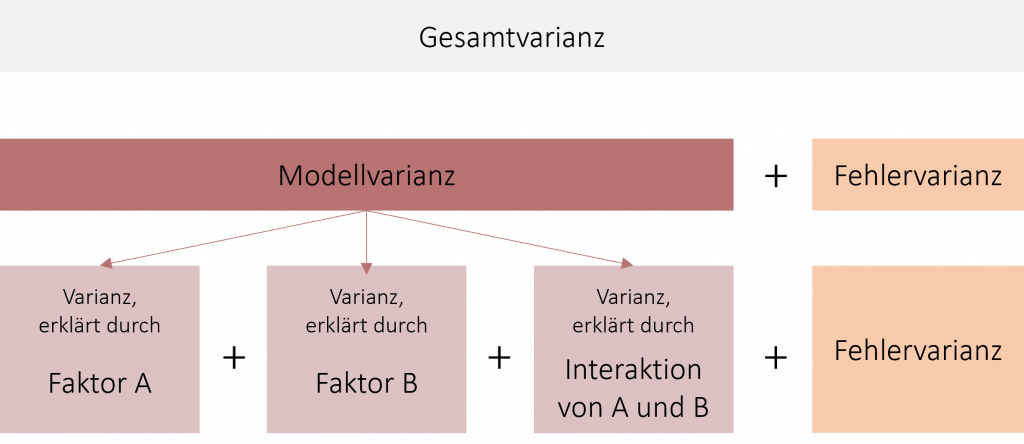
Die Modellvarianz teilt sich daher in drei Teile auf: Die Varianz, die durch Faktor A (Lernmethode) erklärt werden kann; Die Varianz, die durch Faktor B (Geschlecht) erklärt werden kann und die Varianz, die durch die Interaktion beider Faktoren erklärt werden kann. Die ersten beiden bezeichnet man als Haupteffekte, die Kombination beider Faktoren nennt man Interaktionseffekt.
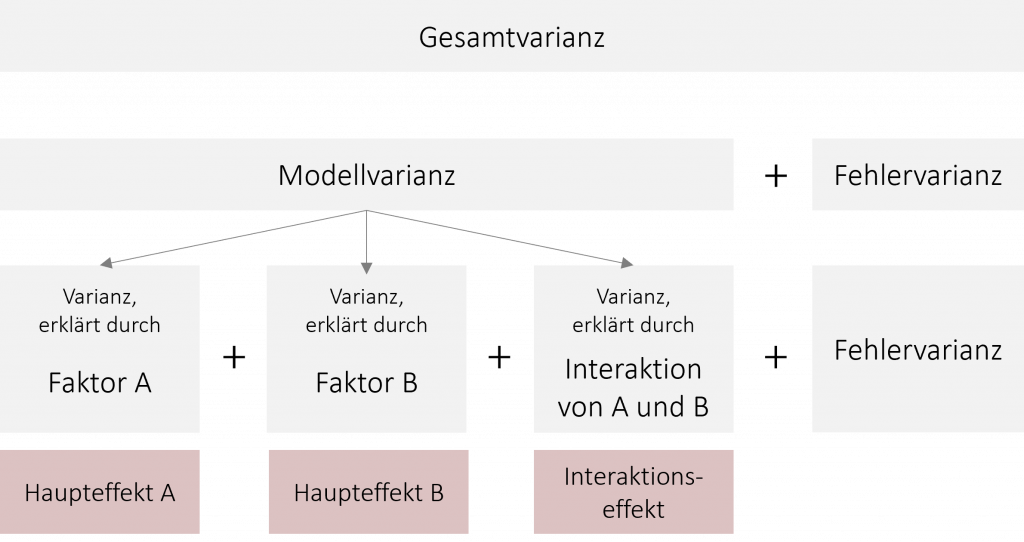

17.4 Haupteffekt
Als Haupteffekt wird der direkte Effekt eines Faktors auf die abhängige Variable bezeichnet. Da wir in der zweifaktoriellen ANOVA zwei Faktoren betrachten, gibt es dementsprechend auch zwei mögliche Haupteffekte. In unserem Bespiel wäre der Einfluss der Lernmethode auf die Einarbeitungszeit Haupteffekt A und der Einfluss des Geschlechts auf die Dauer der Einarbeitung Haupteffekt B.
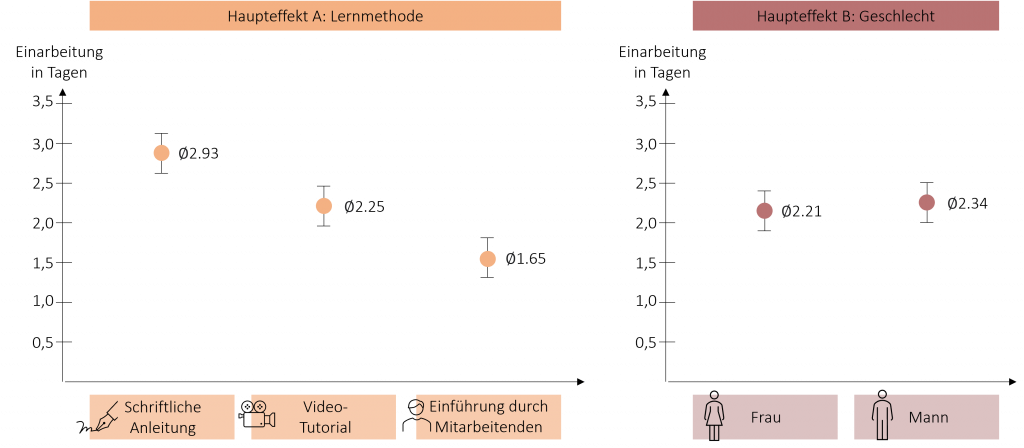
Die beiden Haupteffekte untersuchen die ersten beiden Hypothesen, die wir zuvor aufgestellt haben. Wird ein Haupteffekt signifikant, so gibt es mindestens einen signifikanten Unterschied zwischen der Faktorstufen eines Faktors (unabhängig vom anderen Faktor). Wenn also beispielsweise Haupteffekt A signifikant werden würde, gibt es zwischen den drei Lernmethoden mindestens 1 signifikanten Unterschied (unabhängig vom Geschlecht) im Hinblick auf die Einarbeitungsdauer.
Das folgende Video erklärt Ihnen zudem die Funktionsweise der Berechnung der Haupteffekte an einem Beispiel aus der FiveProfs Burgerkette.
16.2 Mehrfaktorielle Varianzanalyse | Haupteffekte
17.5 Interaktionseffekt
Ein Interaktionseffekt liegt vor, wenn die Wirkungen eines Faktors auf die abhängige Variable von der Ausprägung des anderen Faktors abhängt. In diesem Fall haben die beiden unabhängigen Faktoren, die wir betrachten, einen irgendwie gearteten Zusammenhang. Sie können sich beispielsweise verstärken, abmildern oder sogar ihre Wirkrichtung umkehren. Ob solch eine Interaktion vorliegt, kann man anhand von Interaktionsgrafiken erkennen. Diese zeigen die Mittelwerte der untersuchten Gruppen an, die mithilfe einer Linie hinsichtlich eines der beiden Faktoren verbunden sind. Sind die Linien nicht parallel zueinander, liegt ein Interaktionseffekt vor.
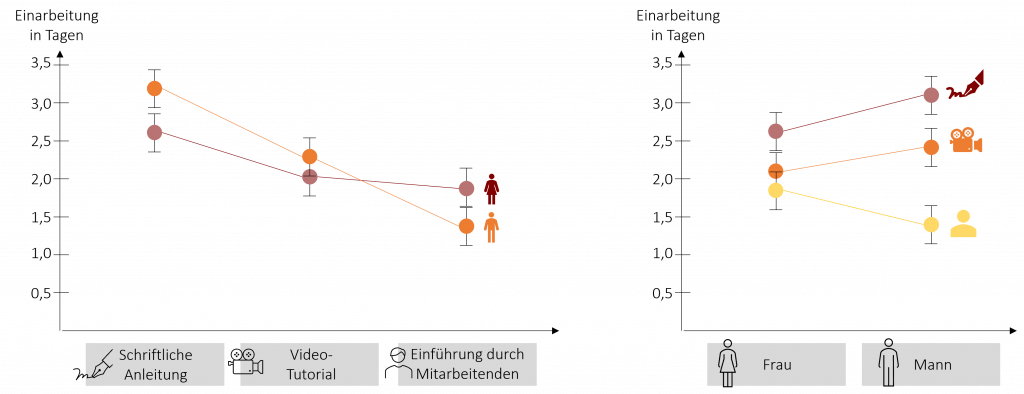
In der Grafik verlaufen die Linien nicht parallel zueinander. In diesem Fall sollten die Faktoren nicht mehr unabhängig voneinander betrachtet werden, da man sonst leicht zu falschen Schlussfolgerungen kommen könnte. Würde man beispielsweise nur die Unterschiede zwischen den drei Lernmethoden (Haupteffekt A) betrachten, könnte man ableiten, dass die Einarbeitung durch einen Mitarbeitenden die beste Lernmethode ist (kürzeste Einarbeitungszeit). Schaut man sich jedoch den Interaktionseffekt an, so sieht man schnell, dass das bei Männern der unterschied sehr deutlich ist, aber bei Frauen Videos gleich gut funktionieren. Die Interpretation der beiden Haupteffekte ist bei einem Interaktionseffekt aus diesem Grund nur bedingt oder gar nicht erst möglich.
Inwiefern man die Haupteffekte interpretierten kann, hängt von der Art der Interaktion ab. Man unterscheidet grundsätzlich zwischen drei Arten von Interaktionen.
Ordinale Interaktion
Bei der ordinalen Interaktion verlaufen die Linien in beiden Interaktionsgrafiken gleichsinnig und überkreuzen sich nicht.
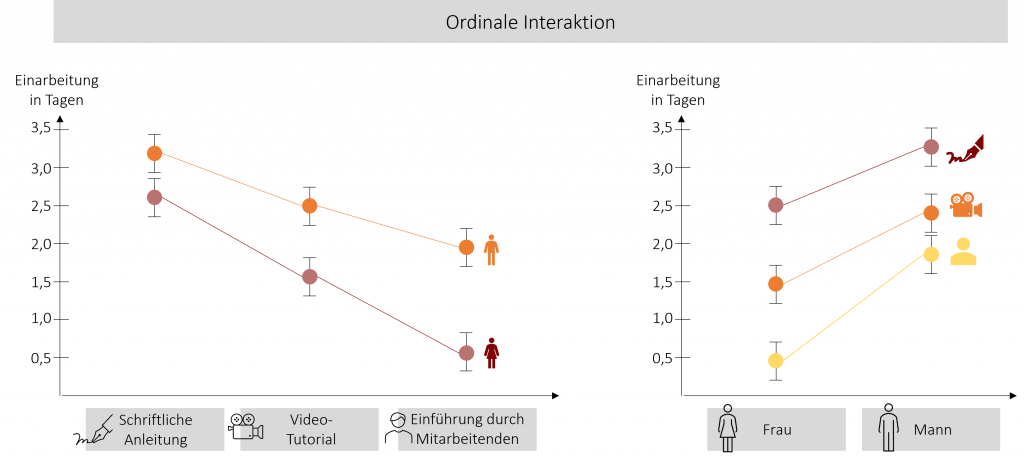
In diesem Fall können die Haupteffekte zwar immer noch interpretiert werden, dennoch sollten sie in Kombination mit dem Interaktionseffekt betrachtet werden. Man kann also sagen, dass die Einarbeitung bei der Lernmethode „Einarbeitung durch einen Mitarbeitenden“ am schnellsten ist (Haupteffekt A) und dass sie bei Frauen im Vergleich zu Männern kürzer ist (Haupteffekt B).
Disordinale Interaktion
Bei einer disordinalen Interaktion überschneiden sich die Linien in beiden Interaktionsgrafiken.
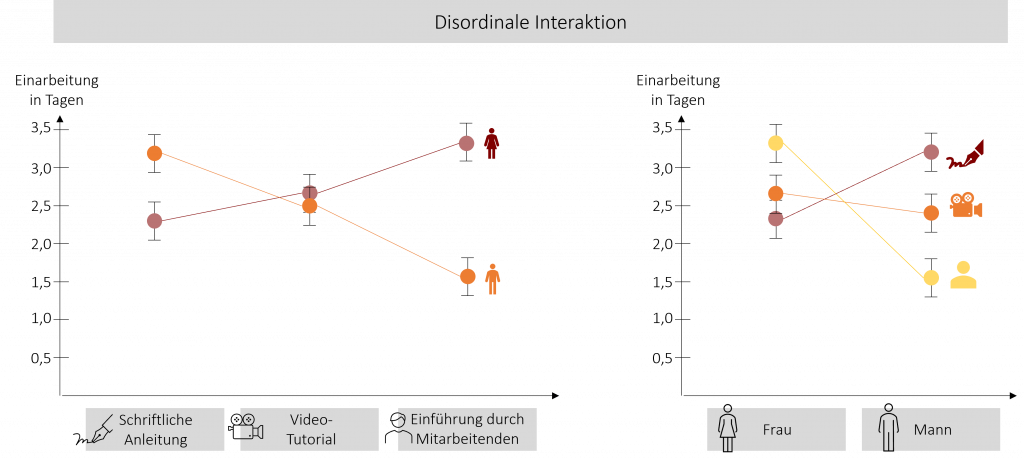
Tritt eine disordinale Interaktion auf, können die Haupteffekte nicht mehr interpretiert werden, da sich ihre Wirkung abhängig vom jeweils anderen Faktor umkehren kann. Man kann also weder sagen, welche Lernmethode die geringste Einarbeitungszeit benötigt, noch welches Geschlecht schneller eingearbeitet werden kann. Die Interpretation muss hierbei für jede Faktorkombination einzeln erfolgen.
Semi-disordinale (hybride) Interaktion
Bei einer hybriden Interaktion überschneiden sich die Linien in nur einer der beiden Interaktionsgrafiken.
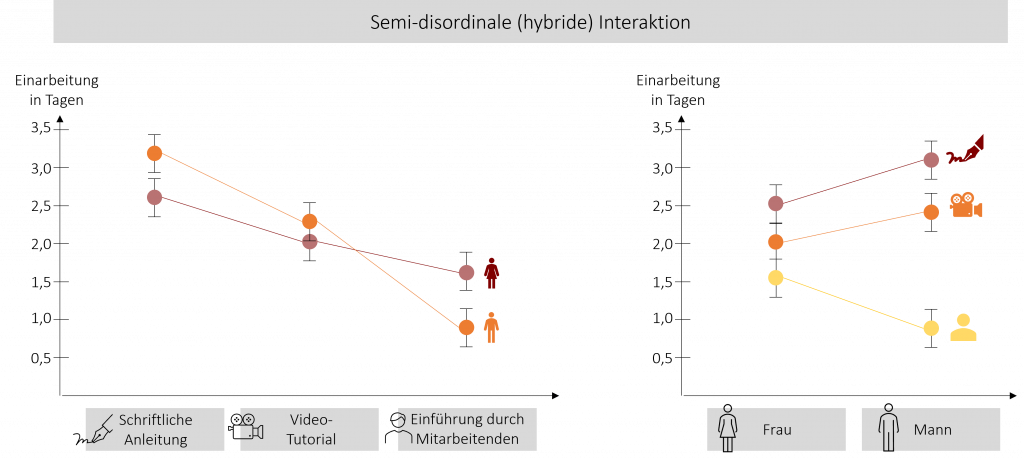
In diesem Fall kann nur einer der beiden Haupteffekte unabhängig interpretiert werden. Im obigen Bild kann beispielsweise Haupteffekt „Lernmethode“ interpretiert werden: Die Lernmethode „Einführung durch einen Mitarbeitenden“ benötigt im Vergleich zu den anderen Lernmethoden die geringste Einarbeitungszeit (unabhängig vom Geschlecht). Der Haupteffekt des Geschlechts kann hingegen nicht mehr unabhängig interpretiert werden, da sich die Linien überschneiden. Man kann also nicht sagen, ob Frauen oder Männer grundsätzlich schneller bei der Einarbeitung sind – es hängt ganz von der Lernmethode ab.
Keine Interaktion
Verlaufen beide Linien parallel, liegt keine Interaktion vor.
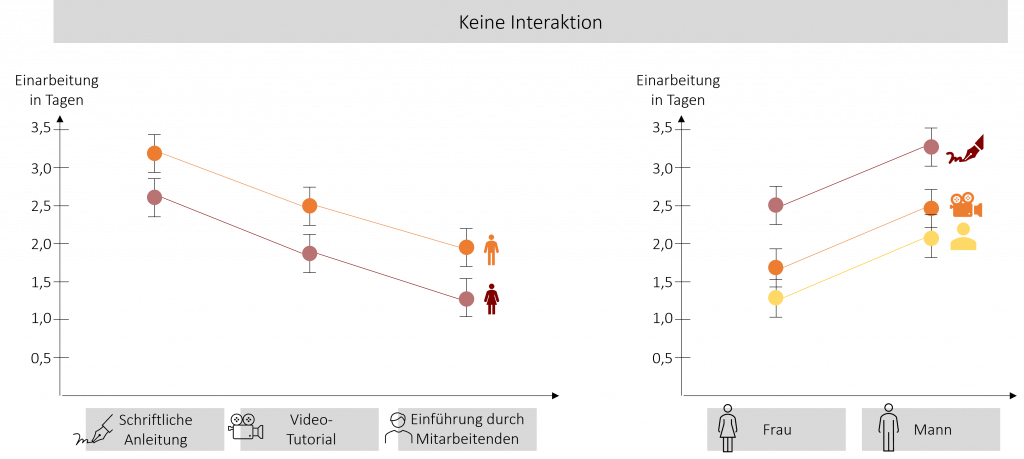
Hierbei können beide Haupteffekt unabhängig voneinander und uneingeschränkt interpretiert werden.
Alles verstanden? Wenn nicht, dann erklärt Ihnen das nachfolgende Video den Interaktionseffekt anhand eines weiteren Beispiels.
16.3 Mehrfaktorielle Varianzanalyse | Interaktionseffekt
17.6 Durchführung und Ergebnisinterpretation
In der Praxis führen Sie die zweifaktorielle Varianzanalyse mithilfe von statistischen Programmen wie SPSS oder R durch. Wie Sie dabei in SPSS vorgehen müssen, erfahren Sie im folgenden Video:
16.9 Mehrfaktorielle Varianzanalyse | SPSS Rechenbeispiel
Am Ende erhalten Sie sowohl in SPSS als auch in R einen Ergebnis-Output. Dieser sieht in den meisten Fällen so oder so ähnlich aus (abhängig vom Programm und der Version).
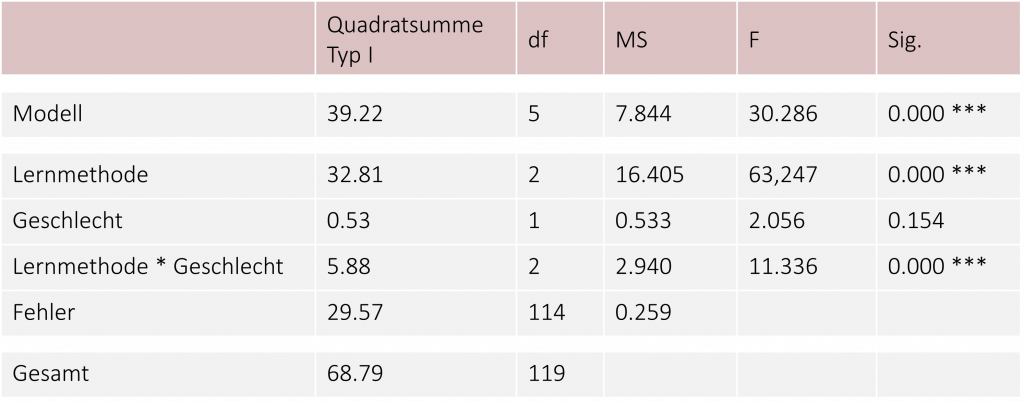
Schauen wir uns die Ergebnisse für unser Beispiel einmal genauer an. Die erste Zeile betrachtet die gesamte Modellvarianz:
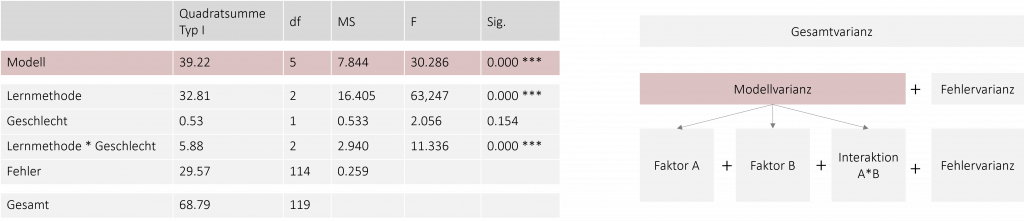
Die Zeile überprüft dabei die These, ob im gesamten Modell, also zwischen den 6 Gruppen, die wir betrachten, mindestens ein signifikanter Unterschied besteht. Wird der F-Wert in dieser Zeile signifikant (p < .005), wissen wir, dass sich mindestens 2 Gruppen (unserer 6 Gruppen) in irgendeiner Weise voneinander unterscheiden. Was wir jedoch noch nicht wissen ist, zwischen welchen Gruppen der Unterschied besteht und ob die Unterschiede auf die Haupteffekte oder den Interaktionseffekt zurückgehen. Dafür schauen wir in die nächsten Zeilen:
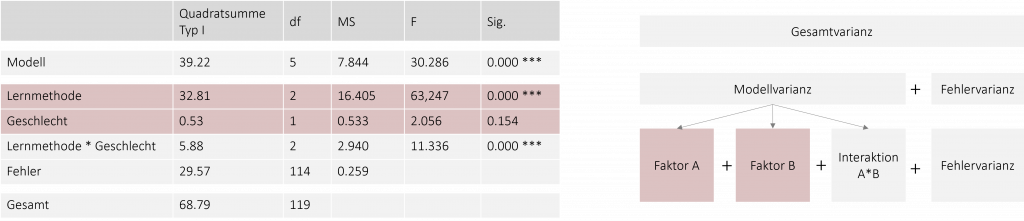
Die nächsten beiden Zeilen zeigen uns, ob die beiden Haupteffekte signifikant geworden sind. Die erste der beiden Zeilen bildet hierbei den Haupteffekt „Lernmethode“ und die zweite Zeile den Haupteffekt „Geschlecht“ ab. Wird der F-Wert in einer der beiden Zeilen signifikant, liegt mindestens ein signifikanter Unterschied zwischen den Faktorstufen des jeweiligen Faktors vor. In unserem Beispiel haben wir einen signifikanten Haupteffekt der Lernmethode. Das bedeutet, dass zwischen den drei Lernmethoden mindestens ein Unterschied besteht (unabhängig vom Geschlecht). Aber Vorsicht: noch dürfen wir die Haupteffekte nicht interpretieren, da wir nicht wissen, ob sie unabhängig betrachtet werden können oder in irgendeiner Form zusammenwirken. Dies verrät uns die nächste Zeile, die den Interaktionseffekt abbildet:
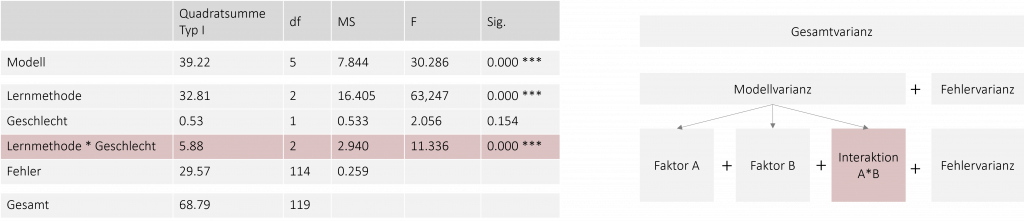
Ist die Zeile signifikant, sind die beiden Faktoren nicht unabhängig voneinander, sondern weisen irgendeinen Zusammenhang auf. Es liegt eine Interaktion vor. Bezogen auf unser Beispiel bedeutet dies, dass die Einarbeitungszeit zwischen den drei Lernmethoden abhängig vom Geschlecht ist. Um nun herauszufinden welche Art der Interaktion auftritt und ob wir die Haupteffekte überhaupt interpretieren dürfen, müssen wir post-hoc Analysen durchführen.
Die letzte Zeile zeigt uns die Fehlervarianz an. Sie beschreibt die Varianz der abhängigen Variable, die auf unsystematische Einflüsse zurückgeht. Die Werte sind lediglich für die Berechnung der F-Werte interessant, jedoch für die Interpretation der Effekte nicht weiter von Bedeutung.
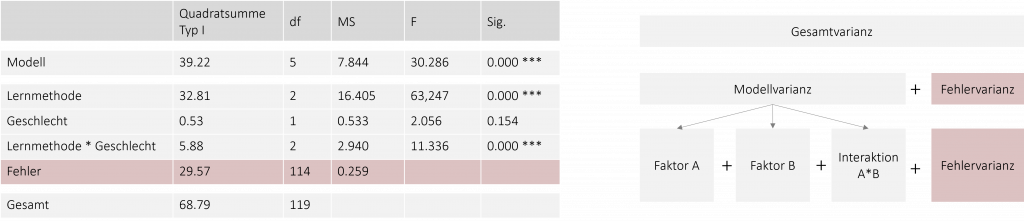
Natürlich können Sie jeden dieser Werte im Output auch per Hand ausrechnen. Die dazu nötigen Formeln haben Sie bereits im letzten Kapitel kennengelernt. Das nachfolgende Video erklärt Ihnen die Berechnung der einzelnen Werte sowie deren Bedeutung anhand eines Beispiels aus der FiveProfs-Kette.
16.6 Mehrfaktorielle Varianzanalyse | Funktionsweise
Auch die p-Werte (Signifikanzen) können mit Hilfe von Tabellen selbstständig berechnet werden. Wie genau das funktioniert und wie die Werte anschließend zu interpretieren sind, erklärt Ihnen das folgende Video.
16.7 Mehrfaktorielle Varianzanalyse | Interpretation
17.7 Post-hoc Verfahren
Anhand der Ergebnistabelle wissen wir noch nicht, zwischen welchen Gruppen die Unterschiede genau auftreten, was wir für einen Interaktionseffekt haben und ob wir die Haupteffekte überhaupt interpretieren können oder nicht. Um diese Fragen zu beantworten, helfen uns die post-hoc Verfahren.
Um die genauen Unterschiede zwischen den Gruppen zu lokalisieren, können wir auf dieselben Verfahren wie bei der einfaktoriellen Varianzanalyse zurückgreifen. Da diese im letzten Kapitel bereits beschrieben wurden folgt im weiteren lediglich eine kurze Auflistung:
- A-priori Kontraste
Diese können eingesetzt werden, wenn man bereits im Vorhinein gerichtete Hypothesen über bestimmte Unterschiede zwischen den Gruppen hat. Das Verfahren hat den Vorteil, dass es bei der Überprüfung auf Unterschiede keine Teststärke verliert. - Post-hoc-Tests
Mögliche Post-hoc-Tests sind Multiple t-Tests mit Bonferroni Korrektur oder alternativ: Tukey-B-Test (bei gleich großen Gruppen), GT2 nach Hochberg (bei unterschiedlich großen Gruppen und Varianzhomogenität) und Games Howell (bei Varianzheterogenität). Alle Tests haben den Nachteil, dass sie Teststärke einbüßen und es dementsprechend schwerer ist signifikante Unterschiede zwischen zwei Gruppen zu finden. - Graphischer Vergleich der Gruppen mit Fehlerbalken

Was uns jedoch neben der Lokalisierung der Unterschiede interessiert, ist welcher Interaktionseffekt vorliegt (falls dieser in der Tabelle signifikant geworden ist). Hierfür schauen wir uns die Interaktionsgrafiken an, die Sie bereits weiter oben im Kapitel kennengelernt haben. Bei der Interpretation der Grafiken können wir auf zwei wesentliche Merkmale achten:

- Linienführung
Verlaufen die Linien parallel zueinander? (Wenn ja, dann liegt keine Interaktion vor). Überschneiden sich die Linien? (Wenn ja, liegt eine disordinale oder hybride Interaktion vor; Wenn nicht, dann handelt es sich um eine ordinale Interaktion) - Konfidenzintervalle
Überschneiden sich die Konfidenzintervalle der einzelnen Faktorstufen? (Wenn nein, dann liegt zwischen diesen Faktorstufen ein signifikanter Unterschied vor).
Durch die Interaktionsgrafiken wissen wir nun, was für eine Interaktion vorliegt. Bei einer ordinalen oder hybriden Interaktion können wir anschließend die Haupteffekte nochmals betrachten und diese bei Bedarf interpretieren. Bei einer disordinalen Interaktion ist eine Interpretation der Haupteffekte, wenig zielführend. Hier wird üblicherweise nur der Interaktionseffekt interpretiert.
Das nachfolgende Video zeigt Ihnen abschließend anhand eines Beispiels, wie Sie die Interaktionsgrafiken interpretieren können.
16.8 Mehrfaktorielle Varianzanalyse | Post-Hoc Verfahren
17.8 Übungsfragen
Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!
In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!

