Varianz- und Regressionsanalyse
16 Einfaktorielle Varianzanalyse (ANOVA)
16.0 Einführung Varianzanalyse
Mit Hilfe der Varianzanalyse können wir herausfinden, ob sich die Mittelwerte von 3 oder mehr Gruppen signifikant voneinander unterscheiden. Sie beantwortet damit die selbe Fragestellung wie der t-Test für unabhängige Stichproben, den Sie im letzten Kapitel kennengelernt haben. Dieser kann jedoch im Gegensatz zur Varianzanalyse nur die Mittelwerte von zwei Gruppen vergleichen. Würden wir mit dem t-Test versuchen mehrere Gruppen auf Unterschiede prüfen in dem wir alle Gruppen paarweise vergleichen wäre es deutlich schwieriger einen signifikanten Effekt zu finden, da man hierbei eine Korrektur durchführen muss (dazu später mehr bei den Post-Hoc Verfahren). Die Varianzanalyse umgeht diese Problematik durch den Vergleich von Varianzanteilen, daher auch der Name Varianzanalyse oder englisch ANOVA (Analysis of Variance). Wie das genau funktioniert schauen wir uns nun gemeinsam an.
Mögliche Fragestellungen, die mithilfe der Varianzanalyse beantwortet werden:
- Gibt es einen Unterschied in der Zahlungsbereitschaft zwischen unseren 4 verschiedenen Burger-Sorten?
- Wird die Attraktivität unseres Logos in gelb, rot oder blau unterschiedlich bewertet?
- Gibt es Unterschiede in der Umsatzstärke unserer 12 Five Profs Filialen in Deutschland?
Das folgende Video bietet Ihnen eine Einführung in die Anwendungsfälle der ANOVA.
15.1 Varianzanalyse (ANOVA) | Einführung
16.1 Hypothesen
Im Gegensatz zu den bisherigen Testverfahren, die sie bereits kennengelernt haben, testet die Varianzanalyse nur ungerichtete Hypothesen. Das dazugehörige Hypothesenpaar lautet:
H0: Es gibt keinen Unterschied zwischen den einzelnen Gruppen (auch Faktorstufen genannt) auf der abhängigen Variable.
H1: Es gibt mindestens einen Unterschied zwischen den einzelnen Gruppen auf der abhängigen Variable.
Wir können also mit Hilfe der Varianzanalyse herausfinden, ob zwischen unseren drei, vier oder mehr Gruppen irgendein Unterschied besteht. Zwischen welchen Gruppen genau dieser Unterschied liegt und, ob es nur einen oder sogar mehrere signifikante Unterschiede gibt, erfahren wir hingegen zunächst nicht. Deshalb führt man bei einer signifikanten Varianzanalyse üblicherweise weitere Verfahren durch, um die genauen Unterschiede zu ermitteln. Dies werden Post-hoc Testungen genannt (da sie danach, also „Post-hoc“ durchgeführt werden). Wenn bereits im Vorhinein gerichtete Hypothesen bestehen, gibt es auch die Möglichkeit sogenannte geplante Kontraste durchzuführen. Dieses betrachten wir an dieser Stelle jedoch nicht weiter.
Hypothesenbespiele
- H0: Die Zahlungsbereitschaft für unsere 4 Burgersorten ist gleich (μ1 = μ2 = μ3 = μ4).
H1: Es gibt mindestens einen Unterschied in der Zahlungsbereitschaft zwischen unseren 4 Burgersorten. - H0: Der Umsatz unserer 12 FiveProfs Filialen ist gleich (μ1 = μ2 = μ3 = μ4 = μ5 = μ6 = μ7 = μ8 = μ9 = μ10 = μ11 = μ12)
H1: Es gibt mindestens einen Unterschied im Umsatz in unseren 12 FiveProfs Filialen.
Das folgende Video zeigt Ihnen nochmal anhand einiger Beispiele die Hypothesenbildung bei der ANOVA.
15.2 Varianzanalyse (ANOVA) | Hypothesen
16.2 Voraussetzungen
Bevor wir eine Varianzanalyse durchführen können, müssen wir die Voraussetzungen überprüfen. Bei der ANOVA müssen hierfür folgende Punkte betrachtet werden:
- intervallskalierte abhängige Variable
- Messwerte müssen unabhängig voneinander sein
Sind die Messwerte hingegen nicht unabhängig voneinander (bspw. bei einer Messwiederholung) führen wir statt einer ANOVA eine ANOVA mit Messwiederholung durch. - Normalverteilung der abhängigen Variable in allen Gruppen
Diese Voraussetzung können wir entweder graphisch (bspw. durch die Betrachtung eines Histogramms) oder mittels eines Testverfahrens (bspw. Shapiro-Wilk Test, Kolmogorov-Smirnov-Test, Lilliefors) überprüfen. Die Testverfahren dürfen für die Annahme der Normalverteilung nicht signifikant werden.
Ist eine Normalverteilung nicht gegeben, reagiert die Varianzanalyse meist sehr robust. Insbesondere, wenn die Gruppen gleich groß sind und eine Stichprobengröße von jeweils mehr als 20 Personen aufweisen. Daher wird dieser Voraussetzung in der Praxis weniger Beachtung geschenkt. - Varianzhomogenität der Gruppen
Varianzhomogenität bedeutet, dass die Streuung in den zu vergleichenden Gruppen vergleichbar groß ist.
Diese Voraussetzung wird standardmäßig über den Levene-Test überprüft. Um die Varianzhomogenität zu unterstellen, darf der Test nicht signifikant werden.
Ist hingegen Varianzheterogenität gegeben (der Levene-Test wird signifikant), rechnen wir eine Varianzanalyse mit Welch-Korrektur. Diese wird in SPSS automatisch mit ausgegeben.
15.3 Varianzanalyse (ANOVA) | Voraussetzungen
16.3 Grundsätzliche Funktionsweise
Um die grundsätzliche Funktionsweise der Varianzanalyse zu verstehen, bedienen wir uns eines Beispiels. Stellen Sie sich vor, wir möchten den neuen Mitarbeitenden der FiveProfs Kette beibringen, möglichst schnell leckere Burger zuzubereiten. Hierfür vergleichen wir drei Lernmethoden, die ihnen das Burgerbraten beibringen sollen. 5 Mitarbeitende erhalten eine schriftliche Anleitung, 5 weitere Mitarbeitende lernen die Zubereitung anhand eines Video-Tutorials und weitere 5 Mitarbeitende lernen direkt von einem erfahrenen Kollegen. Nach 3 Tagen wird die Zeit gemessen, die die Mitarbeitenden benötigen, um einen Burger zuzubereiten. Die folgende Grafik zeigen Ihnen die Ergebnisse:
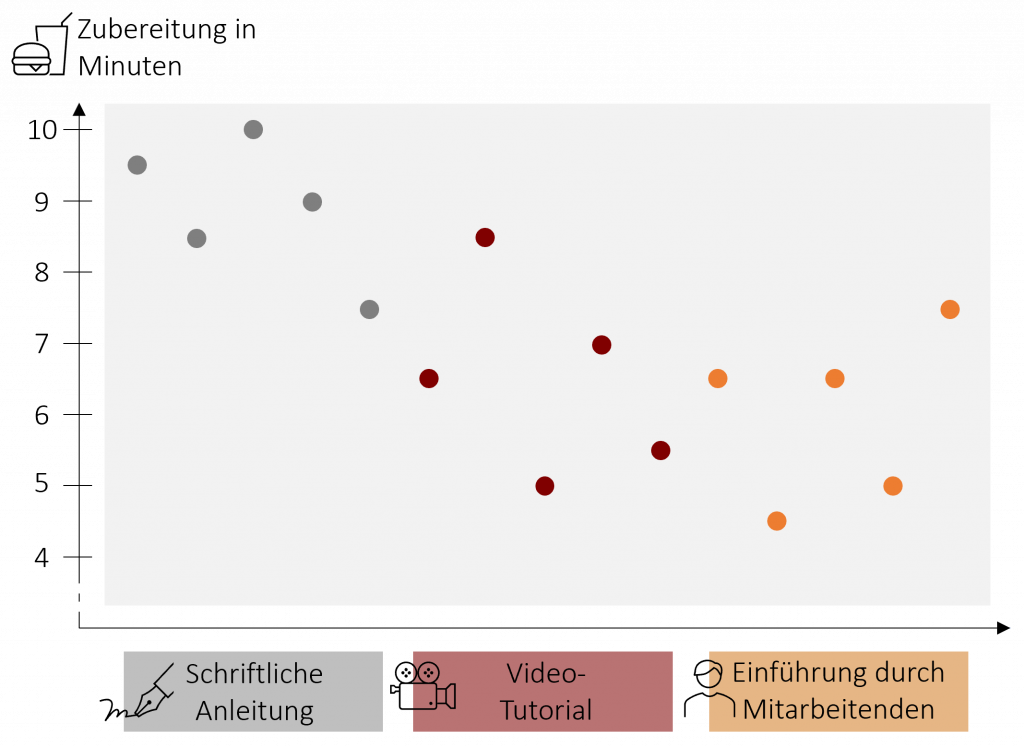
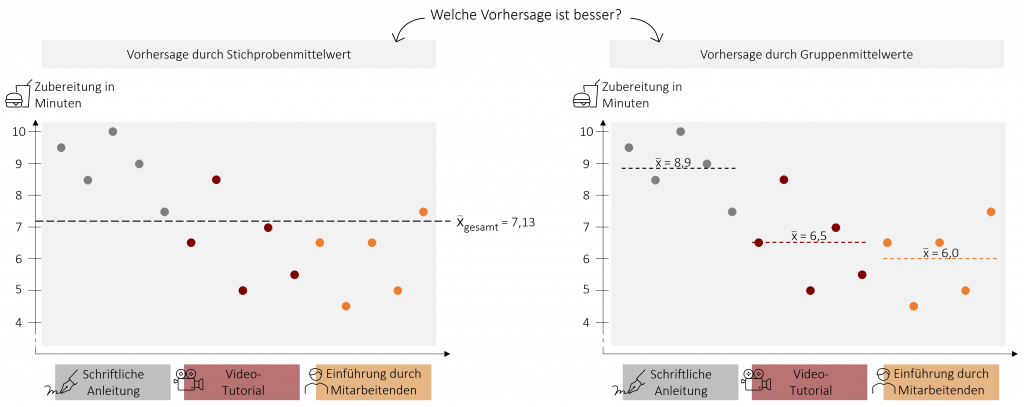
Um herauszufinden, ob eine der drei Lernmethoden besser ist wollen wir nun die drei Mittelwerte vergleichen und müssen daher beurteilen ob sich die Mittelwerte signifikant voneinander unterscheiden. Die Varianzanalyse bedient sich hierbei einem Trick. Sie untersucht, ob der gesamte Mittelwert über alle drei Gruppen (auch Grand Mean genannt) oder die einzelnen Gruppenmittelwerte die erhobenen Daten besser vorhersagen können. In unserem Beispiel untersucht die ANOVA somit, ob der Stichprobenmittelwert von = 7,13 Minuten oder die drei Gruppenmittelwerte (Anleitung = 8,9; Video = 6,5; Mitarbeiter = 6) die Zubereitungszeit der Mitarbeitenden besser vorhersagen. Liefern die Gruppenmittelwerte eine bessere Vorhersage bzw. Schätzung, wird die Varianzanalyse signifikant. Die Grundidee der ANOVA ist also recht einfach: Wenn die einzelnen Gruppenmittelwerte die echten Werte signifikant besser vorhersagen als der Mittelwert über alle Gruppen, dann müssen sich die Gruppenmittelwerte auch signifikant voneinander unterscheiden.
Das nachfolgende Video zeigt Ihnen die grundsätzliche Funktionsweise an einem weiteren Beispiel aus der FiveProfs Kette.
15.4 Varianzanalyse (ANOVA) | Grundsätzliche Funktionsweise
16.4 Quadratsummen
Doch wie genau findet die Varianzanalyse heraus, welcher Mittelwert die erhobenen Daten besser vorhersagt? Sie betrachtet hierzu, wie der Name schon sagt, unterschiedliche Varianzen. Zur Erinnerung: Die Varianz gibt die mittlere Abweichung jedes einzelnen Wertes vom Mittelwert an. Für die Betrachtung der verschiedenen Varianzen werden bei der ANOVA sogenannte Quadratsummen berechnet. Quadratsummen erhält man, wenn man die Abweichung jedes einzelnen Werts vom Mittelwert quadriert und anschließend aufsummiert. Damit sind Quadratsummen nichts anderes als Varianzen, die nicht an der Anzahl der Werte relativiert werden (Gerne nochmal in Kapitel 2 die Berechnung der Varianz anschauen).
Die Varianzanalyse vergleicht bei ihrer Betrachtung drei Varianzen: die Gesamtvarianz, Modellvarianz und Fehlervarianz (Auch das haben wir in Kapitel 5 Regression schon einmal besprochen).
Gesamtvarianz (QStotal)
Die Gesamtvarianz ist ein Maß für die Stärke der Abweichung aller Messwerte vom Gesamtmittelwert (Grand Mean). Sie gibt an, wie stark sich die erhobenen Daten insgesamt voneinander unterscheiden. In der Varianzanalyse wird sie durch die gesamte Quadratsumme (QStotal) angegeben und betrachtet. Ihre Formel lautet wie folgt:
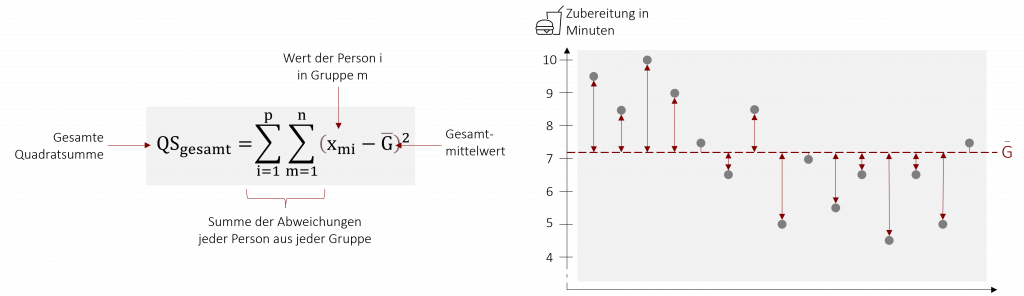
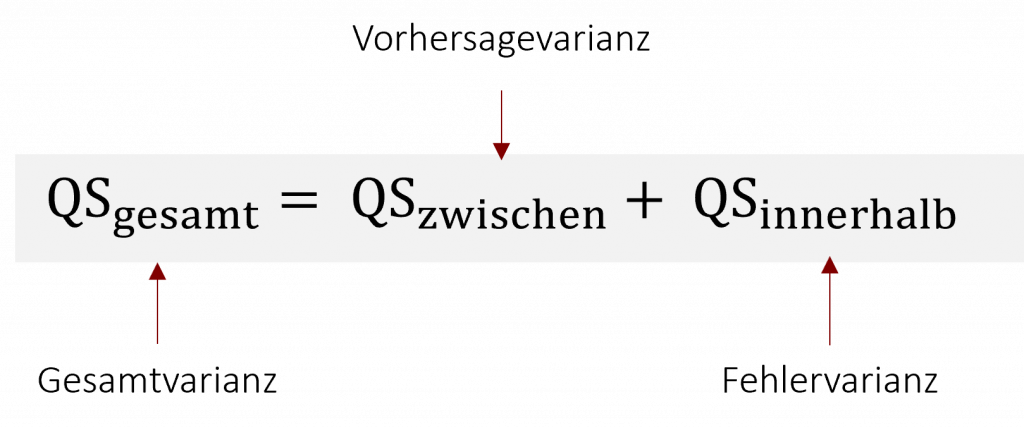
Für diese Gesamtvarianz gibt es in der ANOVA zwei mögliche Ursachen: systematische und unsystematische Einflüsse. Systematische Einflüsse beruhen auf unserem zu untersuchenden Effekt. In unserem Beispiel wäre der systematische Einfluss auf die Streuung der Daten die unterschiedliche Lernmethode, die der jeweilige Mitarbeitende verwendet. Dieser systematisch Einfluss wird in der Vorhersage- oder Modellvarianz betrachtet (QSzwischen). Unsystematische Einflüsse beruhen hingegen auf zufälligen Unterschieden der Versuchsobjekte. Diese Einflüsse werden durch die Fehlervarianz (QSinnerhalb) betrachtet. Die Vorhersage- und die Fehlervarianz ergibt zusammen die Gesamtvarianz.
Vorhersagevarianz (QSzwischen)
Die Vorhersage- oder Modellvarianz gibt die Varianz zwischen den Gruppenmittelwerten an. Sie wird dadurch berechnet, dass man die Abweichungen der einzelnen Gruppenmittelwerte zum Gesamtmittelwert quadriert und aufsummiert.
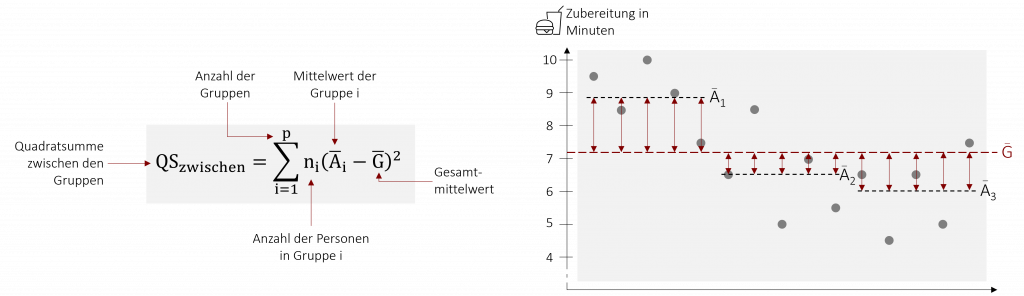
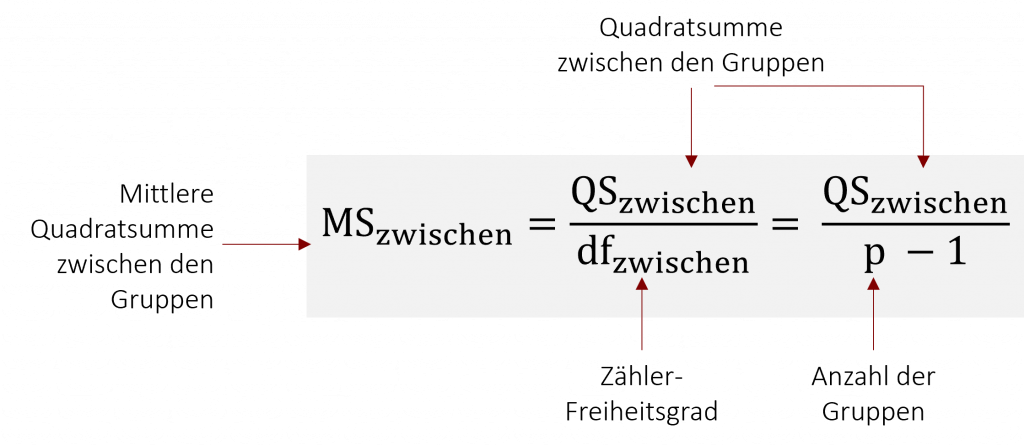
Die Quadratsumme ist jedoch abhängig von der Anzahl der Gruppen. Desto mehr es gibt, desto größer ist sie. Um ein unabhängiges Maß für die Varianz zwischen den Gruppenmittelwerten zu erhalten, relativiert man die Quadratsumme mit den zugehörigen Freiheitsgraden dfzwischen. Man erhält die mittlere Quadratsumme MSzwischen (auch mittleres Abweichungsquadrat genannt).
Beispiel: Burgerbraten lernen
In unserem Beispiel der Zubereitungszeit von Burgern beträgt die Quadratsumme zwischen den Gruppen QSzwischen=24,03. Wir vergleichen 3 verschiedene Lernmethoden.
Wie lautet die mittlere Quadratsumme MSzwischen?
![]()
Fehlervarianz (QSinnerhalb)
Die Fehlervarianz ist der Anteil der Varianz, der auf unsystematischen Einflüssen (bspw. unterschiedlicher Gedächtnisleistung) beruht. Sie berechnet sich durch die Abweichung der tatsächlich gemessenen Werten von den jeweiligen Gruppenmittelwerten und beschreibt damit die Varianz innerhalb der einzelnen Gruppen. Werden die Abweichungen für jeden einzelnen Wert quadriert und aufsummiert, erhalten wir die entsprechende Quadratsumme QSinnerhalb.
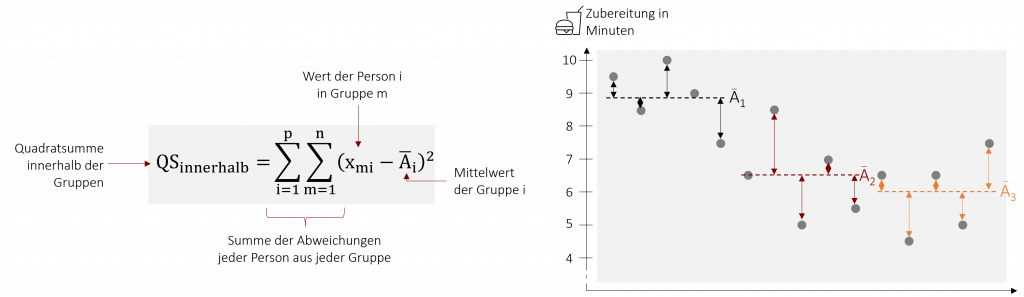
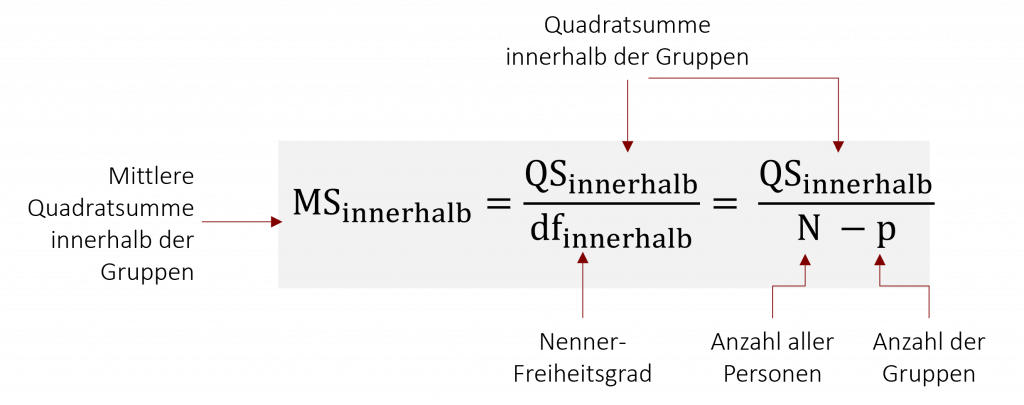
Um auch hier ein unabhängiges Maß für die Streuung innerhalb der Gruppen zu erhalten, relativiert man die Quadratsumme mit Hilfe des entsprechenden Freiheitsgrads dfinnerhalb. So erhält man die mittlere Quadratsumme MSinnerhalb.
Beispiel: Burgerbraten lernen
In unserem Beispiel der Zubereitungszeit von Burgern beträgt die Quadratsumme innerhalb der Gruppen QSinnerhalb=17,20. Hierfür haben wir die Zubereitungszeit von insgesamt 15 Mitarbeitenden gemessen.
Wie lautet die mittlere Quadratsumme MSinnerhalb?
![]()
Übersicht über die Quadratsummen
Die folgende Abbildung zeigt Ihnen nochmals die einzelnen Quadratsummen und ihre Zusammenhänge im Überblick.
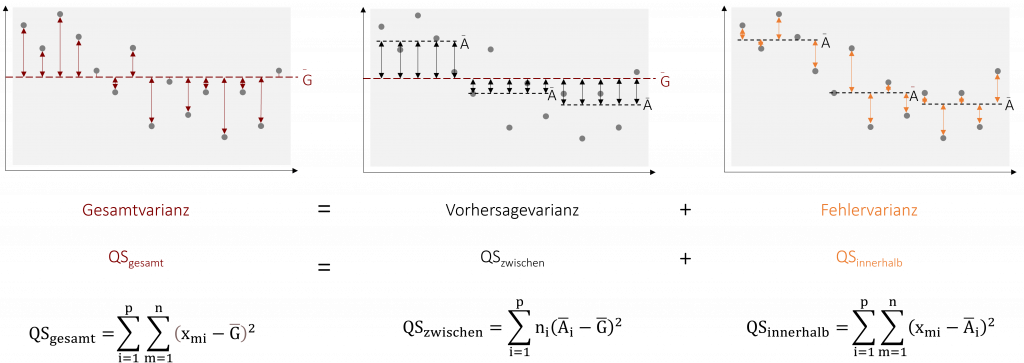
Noch nicht ganz klar? Dann bietet das folgende Video die Möglichkeit die Bedeutung und Berechnung der Quadratsummen anhand eines weiteren Beispiels aus der FiveProfs Kette nachzuvollziehen.
15.5 Varianzanalyse (ANOVA) | Quadratsummen und Freiheitsgrade
16.5 Berechnung der Prüfgröße (F-Wert)
Um nun herauszufinden, ob die Streuung in der Stichprobe auf den Effekt (in unserem Beispiel durch die unterschiedlichen Lernmethoden) oder auf den Zufall zurückzuführen ist, vergleicht man die Varianz zwischen den Gruppen (Vorhersagevarianz) mit der Varianz innerhalb der Gruppen (Fehlervarianz). Dazu wir der Quotient aus den beiden mittleren Quadratsummen gebildet. Man erhält den F-Wert, der die Prüfgröße der Varianzanalyse darstellt (auch das haben wir schon mal recht ähnlich in Kapitel 5 Regression besprochen).

Ist der F-Wert < 1, dann ist die relativierte Fehlervarianz (Varianz innerhalb der Gruppen) größer als die relativierte Vorhersagevarianz (Varianz zwischen den Gruppen). Ist der F-Wert > 1, dann ist die relative Vorhersagevarianz größer als als die relative Fehlervarianz. Im besten Fall ist unser F-Wert somit besonders groß. Die Streuung der Daten geht in diesem Fall vordergründig auf die Gruppenunterschiede und nicht auf mögliche unsystematische Einflüsse zurück. Üblicherweise werden beim F-Wert noch die beiden eben besprochenen Freiheitsgrade (df) in Klammer mit angegeben.
Beispiel: Burgerbraten lernen
Für unser Beispiel lauten die berechneten mittleren Quadratsummen MSzwischen= 12,01 und MSinnerhalb = 1,43. Der daraus resultierende F-Wert ist somit:
![]()
Unser erhaltener F-Wert F(2,12) = 8,40 sagt aus, dass der Anteil der relativen Modellvarianz 8,4 mal größer ist als die der relativierten Fehlervarianz. Das die Unterschiede in den Daten auf Gruppenunterschiede zurückzuführen sind, ist somit relativ wahrscheinlich.
Das nachfolgende Video veranschaulicht Ihnen die Berechnung der F-Werts anhand eines weiteren Beispiels.
15.6 Varianzanalyse (ANOVA) | Berechnung_F-Wert
16.6 Interpretation des F-Werts
Desto größer der F-Wert ist, desto größer ist die Streuung zwischen den einzelnen Gruppen im Vergleich zur Fehlervarianz. Und desto höher die Streuung zwischen den Gruppen, desto eher gibt es signifikante Unterschiede zwischen ihnen. Um unsere Nullhypothese ablehnen zu können und ein signifikantes Testergebnis zu erhalten, möchten wir dementsprechend, dass der F-Wert möglichst hoch ist. Doch ab welchem Wert wird der empirisch bestimmter F-Wert Femp signifikant?
Schauen wir uns diesen Sachverhalt graphisch an. Die F-Verteilung gibt an, wie wahrscheinlich ein bestimmter F-Wert ist. Die F-Verteilung kann, wie auch die bereits besprochene Chi-Quadrat-Verteilung nur positive Werte annehmen. Daher beschränkt sich unser Ablehnungsbereich der Nullhypothese nur auf den oberen Bereich der F-Verteilung. Trotz ungerichteter Hypothese wird der Ablehnungsbereich somit nicht in zwei Hälften aufgeteilt, wie wir es bei anderen Testverfahren kennen.
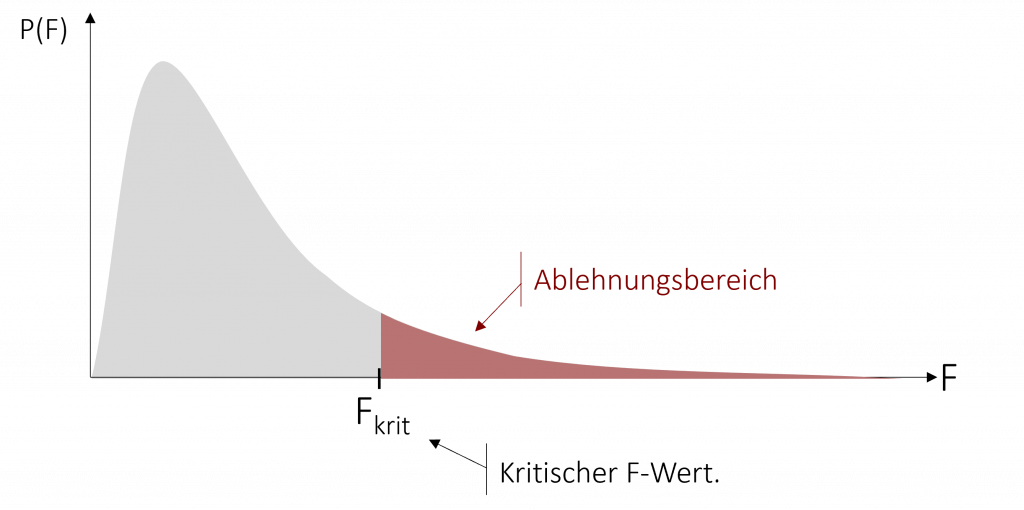
Um die Nullhypothese ablehnen zu können, vergleichen wir unsere empirische Prüfgröße Femp mit der kritischen Ablehnungsgröße Fkrit. Wenn Femp > Fkrit, können wir die Nullhypothese ablehnen. Die kritischen Werte finden Sie in einer Tabelle, die diese Werte für die F-Verteilung abbildet (diese finden Sie zum Beispiel im Anhang dieses Buchs). Ähnlich wie bei der Chi-Quadrat-Verteilung müssen wir um die Tabelle interpretieren zu können die Freiheitsgrade berücksichtigen. Nur in diesem Fall nicht nur einen Freiheitsgrad sondern zwei: Die Tabelle ist nach Zähler- (dfzwischen) und Nenner-Freiheitsgrad (dfinnerhalb) unterteilt. Um den richtigen kritischen F-Wert zu finden, müssen Sie unter den entsprechenden Freiheitsgraden ihr selbstgewähltes Signifikanzniveau wählen.
Beispiel: Burgerbraten lernen
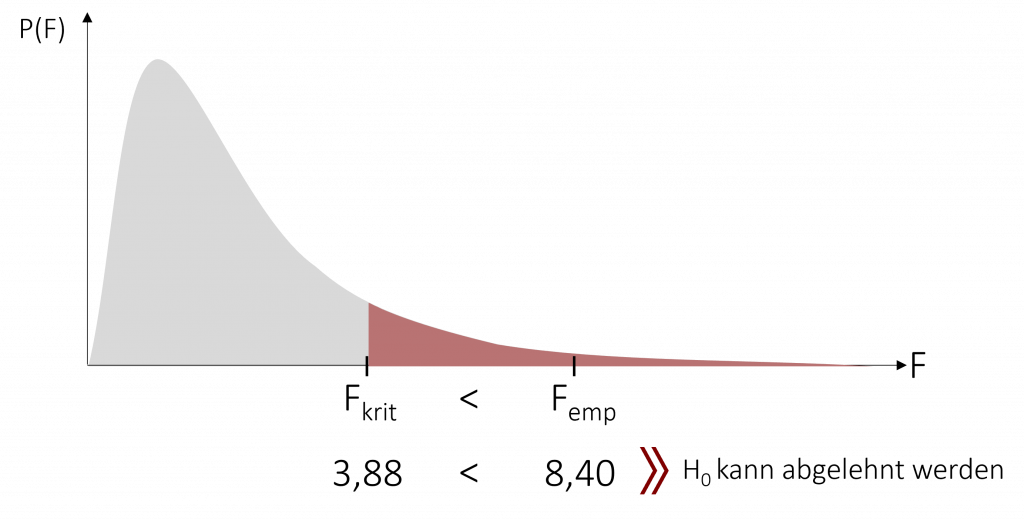
Um herauszufinden, ob sich die 3 Lernmethoden für die Burgerzubereitung signifikant unterscheiden, vergleichen wir unseren empirischen F-Wert Femp = 8,40 mit einem gewählten Signifikanzniveau von α = 5%. Um den richtigen Wert in der Tabelle zu finden, müssen wir zunächst unsere Freiheitsgrade berechnen:
![]()
Anschließend suchen wir den entsprechenden kritischen F-Wert in der Tabelle für das Signifikanzniveau α = 5%.
Wir erhalten einen kritischen F-Wert von Fkrit=3,885.
Da Femp > Fkrit, kann die Nullhypothese abgelehnt werden. Zwischen den 3 Lernmethoden gibt es mindestens einen signifikanten Unterschied in der Burgerbratzeit.
Das nachfolgende Video erklärt Ihnen an einem Beispiel, wie Sie den richtigen F-Wert in den Tabellen finden und zeigt Ihnen zudem die Interpretation des zugehörigen SPSS Outputs.
15.7 Varianzanalyse (ANOVA) | Interpretation
Noch nicht genug? Das folgende Video gibt ein weiteres Beispiel für die Durchführung der Varianzanalyse.
15.8 Varianzanalyse (ANOVA) | Weiteres Beispiel
16.7 Post-hoc-Verfahren
Wenn die Varianzanalyse signifikant wird, wissen wir, dass zwischen den betrachteten Gruppen mindestens ein signifikanter Unterschied besteht. Zwischen welchen Gruppen genau dieser Unterschied liegt und ob es nur einen oder sogar mehrere signifikante Unterschiede gibt, erfahren wir hingegen nicht. Deshalb führt man nach der Varianzanalyse anschließend Post-hoc-Verfahren durch, die die Unterschiede zu lokalisieren.
Multiple t-Tests mit Bonferroni Korrektur
Eine Möglichkeit herauszufinden, zwischen welchen Gruppen ein signifikanter Unterschied besteht, ist die Durchführung von multiplen t-Tests. Da wir wir jedoch bei diesen t-Tests immer wieder die selben Gruppen gegeneinander testen, ist die Voraussetzung der unabhängigen Stichproben verletzt. Der α-Fehler (bspw. 5%) steigt hierdurch automatisch an. Man spricht auch von α-Fehler-Kumulation. Um dem zu entgegnen, führen wir eine Korrektur des α-Fehlers durch.
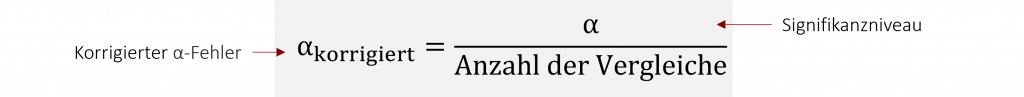
Unseren empirischen p-Wert vergleichen wir anschließend mit dem eben berechneten korrigierten α-Fehler, welchen wir als neues Signifikanzniveau ansetzen. Ist der empirische p-Wert kleiner als der αkorrigiert , liegt ein signifikanter Unterschied zwischen den Gruppen vor.
Nachteil der multiplen t-Tests ist die verringerte Teststärke. Durch den korrigierten α-Fehler ist es deutlich schwerer ein signifikantes Ergebnis zu erhalten.
Beispiel: Burgerbraten lernen
Nach unserer Signifikanten Varianzanalyse, möchten wir herausfinden zwischen welchen der 3 Lernmethoden signifikante Unterschiede bestehen. Zwischen den drei Gruppen sind insgesamt 3 Vergleiche möglich. (Wichtig: Bei einer anderen Gruppenanzahl , entspricht die Anzahl der Vergleiche nicht der Gruppengröße, haben wir zum Beispiel 4 Gruppen gibt es 5 mögliche Paare).
Wenn wir nun t-Tests durchführen möchten, müssen wir gegen folgendes korrigierten α-Niveau testen:
![]()
Weitere Post-hoc-Verfahren
Alternativen zu den multiplen t-Test mit Bonferroni Korrektur sind:
- Weitere Varianten der multiplen t-Testung mit unterschiedlicher Fehlerkorrektur
Beispielsweise der Tukey-B-Test bei gleichgroßen Gruppen, der GT2 nach Hochberg bei unterschiedlich großen Gruppen und Varianzhomogenität sowie der Games-Howell-Test bei Varianzheterogenität. - Graphische Überprüfung
Durch den Vergleich der Konfidenzintervalle der einzelnen Gruppenmittelwerte können ebenfalls Unterschiede lokalisiert werden. Hierzu überprüft man, ob es Gruppen gibt, deren Fehlerbalken sich nicht überlappen. Gibt es keine Überschneidung, ist der Unterschied zwischen den zwei Gruppen signifikant.
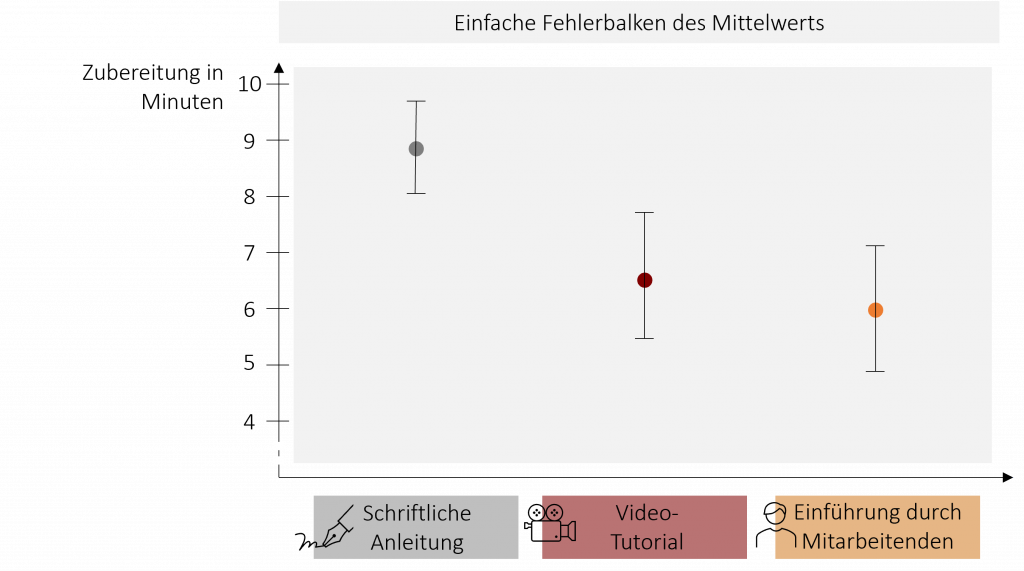
- Geplante Kontraste (A-priori-Kontraste)
Mit Hilfe von geplanten Kontrasten kann man im Vorhinein definierte gerichtete Hypothesen testen. Das Verfahren büßt im Gegensatz zu den multiplen t-Tests nicht an Teststärke ein. Die Kontraste müssen jedoch vor der Untersuchung festgelegt werden, weshalb das Verfahren strenggenommen nicht zu den Post-hoc-Tests hinzugezählt werden kann.
15.9 Varianzanalyse (ANOVA) | Post-Hoc Verfahren
16.8 Effektgröße
Mit Hilfe der Post-hoc-Tests wissen wir, wie viele Unterschiede bestehen und zwischen welchen Gruppen diese liegen. Was wir jedoch noch nicht beantworten können ist, wie groß diese Unterschiede der Gruppen in der Varianzanalyse sind. Diese Frage beantwortet uns die Effektgröße. Für die Varianzanalyse ist die zugehörige Effektgröße η² (Eta²). η² gibt den Anteil der Modellvarianz an der Gesamtvarianz an und berechnet sich indem man den Quotienten der beiden zugehörigen Quadratsummen bildet.

Die Interpretation der Effektgröße erfolgt anschließend nach Cohen (1988) wie folgt:
| Effektgröße | η² |
| klein | .01 |
| mittel | .06 |
| groß | .14 |
15.10 Varianzanalyse (ANOVA) | Effektgröße
Wie die Varianzanalyse sowie die Post-hoc-Tests in SPSS durchgeführt werden, zeigt Ihnen abschließend folgendes Video:
15.11 Varianzanalyse (ANOVA) | Rechenbeispiel SPSS
16.9 Übungsfragen
Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!
In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!

 = 7,13 Minuten
= 7,13 Minuten

