Vorbereitung

Datensatz einlesen

load("WPStudis.RData")

Wir schalten die wissenschaftliche Notation aus, damit uns auch alle Vor- und Nachkommastellen angezeigt werden (Diese werden sonst durch e+10 Notationen abgekürzt)

options(scipen = 999)

t-Tests für eine Stichprobe

Ein t-Test für eine Stichprobe ist ein statistischer Test, mit dem festgestellt werden kann, ob sich der Mittelwert einer Grundgesamtheit von einem bestimmten Wert (meist dem bekannten Mittelwert der Population) unterscheidet. Die Nullhypothese des t-Tests mit einer Stichprobe lautet, dass der Mittelwert der Stichprobe gleich dem Mittelwert der Grundgesamtheit ist. Die Alternativhypothese lautet, dass der Mittelwert der Stichprobe vom Mittelwert der Grundgesamtheit abweicht.

Beim t-Test wird der berechnete t-Wert mit einem kritischen Wert aus der t-Verteilungstabelle auf der Grundlage des Stichprobenumfangs und des Signifikanzniveaus (Alpha) verglichen. Ist der berechnete t-Wert größer als der kritische Wert, deutet dies darauf hin, dass der Mittelwert der Grundgesamtheit von dem angenommenen Wert abweicht, und die Nullhypothese wird verworfen. Wenn der berechnete t-Wert kleiner als der kritische Wert ist, deutet dies darauf hin, dass sich der Mittelwert der Grundgesamtheit nicht von dem hypothetischen Wert unterscheidet, und die Nullhypothese wird nicht zurückgewiesen.

In R können Sie die Funktion t.test() verwenden, um einen t-Test für eine Stichprobe durchzuführen. Sie benötigt mehrere Argumente wie den Datensatz, den Hypothesenwert, die Alternativhypothese und das Signifikanzniveau.

Beispiel
Die 18- bis 25-jährigen Frauen in Deutschland haben aktuell eine durchschnittliche Größe von 166 Zentimetern. Wir wollen prüfen, ob sich die weiblichen Studierenden im Datensatz vom Bundesdurchschnitt unterscheiden.

Zunächst müssen wir die Voraussetzungen prüfen. Diese sind im Einstichproben-Fall:

1. Intervallskalierung. Dies ist bei der Koerpergroesse gegeben
2. Normalverteilung. Diese darf bei n>30 nach dem zentralen Grenzwerttheorem für die Wahrscheinlichkeitsverteilung angenommen werden.

Wir brauchen zunächst eine Variable, die nur die weiblichen Studierenden enthält. Hierfür nutzen wir die which Funktion in der Index Notation (eckige Klammern).

WP_Studentinnen <- WPStudis$F4_Koerpergroesse[which(WPStudis$F3_Geschlecht=="Weiblich")]

Nun können wir den t-Test durchführen. Hierzu geben wir als erstes Argument die Variable an, gefolgt von “mu”, das für den Mittelwert der Population steht und dem griechischen µ (mi) entspicht. Dieser Wert muss bekannt sein, nur dann können wir einen t-Test für eine Stichprobe berechnen.

t.test(WP_Studentinnen, mu=166)
## 
##  One Sample t-test
## 
## data:  WP_Studentinnen
## t = 2.3598, df = 76, p-value = 0.02085
## alternative hypothesis: true mean is not equal to 166
## 95 percent confidence interval:
##  166.2553 169.0174
## sample estimates:
## mean of x 
##  167.6364

Das Ergebnis ist ein t-Wert von 2,36 bei 76 Freiheitsgraden. Diesen Wert könnten Sie mit einem kritischen t-Wert vergleichen, den Sie in einer Tabelle der t-Verteilung finden (z. B. im Anhang unter www.satistikgrundlagen.de). Alternativ und deutlich einfacher ist die Interpretation des p-Werts. Ist der p-Wert kleiner als das gewählte Signifikanzniveau (in der Regel 0,05), können Sie die Nullhypothese, dass der Stichprobenmittelwert gleich dem Populations-Mittelwert ist, ablehnen. Da hier der Wert 0,02 ist, können wir also sagen, dass sich die weiblichen Studierenden im Datensatz hinsichtlich ihrer Körpergröße signifikant vom Bundesdurchschnitt unterscheiden.

Einseitiger t-Test

Bei einem einseitigen t-Test kann die Alternativhypothese als “kleiner” oder “größer” angegeben werden, um die Richtung des Unterschieds zwischen dem Mittelwert der Grundgesamtheit und dem Stichproben-Wert anzugeben.

Wenn die Alternativhypothese als “less” angegeben wird, bedeutet dies, dass angenommen wird, dass der Mittelwert der Stichprobe kleiner ist als der Populations-Wert ist. Wenn die Alternativhypothese mit “greater” angegeben wird, bedeutet dies, dass der Mittelwert der Stichprobe größer als der Populations-Wert angenommen wird. In diesem Fall sucht der Test nach Beweisen dafür, dass der Mittelwert der Stichprobe höher ist als der Populations-Wert.

Sie können die Alternativhypothese in der t.test()-Funktion von R durch Verwendung des alternative Arguments angeben.

Wenn wir die Hypothese testen wollen, ob die WP-Studentinnen größer sind als der Bundesdurchschnitt, geht das so:

t.test(WP_Studentinnen, mu=166, alternative="greater")
## 
##  One Sample t-test
## 
## data:  WP_Studentinnen
## t = 2.3598, df = 76, p-value = 0.01043
## alternative hypothesis: true mean is greater than 166
## 95 percent confidence interval:
##  166.4817      Inf
## sample estimates:
## mean of x 
##  167.6364

Der p-Wert des einseitigen Tests entspricht dem halben p-Wert des zweiseitigen Tests. Daher ändert sich nichts an der Interpretation des Tests (siehe oben)

Einseitige Tests sollten jedoch fundiert theoretisch begründet sein. Im Zweifel sollten Sie daher immer einen zweiseitigen Test durchführen.

In diesem Video zeige ich, wie das in R funktioniert:

Übung

Führen Sie einen einseitigen Hypothesentest für die Hypothese durch: Studierende brauchen ein groesseres Einkommen zum Glücklichsein, als die Population. Der Mittelwert des Einkommens zum Glücklichsein in der Population wurde in einer repräsentativen Befragung ermittelt: 1.620 EUR.

Wie wäre das Ergebnis, wenn wir zweiseitig testen?

Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.

t-Tests für unabhängige Stichproben

Ein unabhängiger t-Test ist ein statistisches Verfahren, mit dem festgestellt werden kann, ob ein signifikanter Unterschied zwischen den Mittelwerten zweier unabhängiger Gruppen besteht. Er wird verwendet, um die Mittelwerte zweier Datengruppen zu vergleichen und festzustellen, ob es einen statistisch signifikanten Unterschied zwischen den Mittelwerten der beiden Gruppen gibt. Der t-Test setzt voraus, dass die Daten metrisch skaliert sind und in beiden Gruppen normal verteilt sind. Zudem müssen die Varianzen der beiden Gruppen gleich sein, also Varianzhomogenität vorliegen.

Beispiel

Wir wollen herausfinden, ob sich die Zufriedenheit (F21_01_Zufriedenheit_Leben) zwischen Studierenden, die Single sind und Studierenden, die in einer Partnerschaft leben, unterscheidet (F19_Partnerschaft)

Deskriptive Analyse

Wir wollen zunächst deskriptiv betrachten, ob sich die Mittelwerte in beiden Gruppen unterscheiden.

Mit der tapply Funktion können wir die Mittelwerte tabellarisch vergleichen.

tapply(WPStudis$F21_01_Zufriedenheit_Leben,WPStudis$F19_Partnerschaft, mean, na.rm = TRUE)
##     Nein       JA 
## 3.736842 4.058824

Ausführlichere Variante aus dem psych Paket:

library(psych)
describeBy(WPStudis$F21_01_Zufriedenheit_Leben,WPStudis$F19_Partnerschaft, mat=TRUE)
##     item group1 vars  n     mean        sd median  trimmed mad min
## X11    1   Nein    1 38 3.736842 0.8909215      4 3.812500   0   1
## X12    2     JA    1 51 4.058824 0.6453453      4 4.097561   0   1
##     max range       skew  kurtosis         se
## X11   5     4 -0.8232281 0.8565148 0.14452655
## X12   5     4 -1.8008958 8.1210900 0.09036642

Voraussetzungen prüfen

Skalenniveau
Zufriedenheit mit dem Leben könnte auch als ordinal skaliert betrachtet werden, da es nur fünf verschiedene Ausprägungen hat (0 = sehr unzufrieden bis 5 = sehr zufrieden). Da solche Skalen in der Praxis oft als intervallskaliert angenommen werden (per Fiat messung), machen wir es im Folgenden auch so.

Normalität

Alternativen zur Prüfung auf Normalität:

1. Histogramm der Verteilung der beiden Gruppen anzeigen lassen, um die Normalität der Daten optisch zu beurteilen
2. Einen Test der Verteilung durchführen z. B. Kolmogorov-Smirnov-Test oder Shapiro-Wilk Test (shapiro.test() )

Aufgrund der Größe der Stichprobe jedoch in diesem Fall vernachlässigbar. Da beide Gruppen größer als n>30 sind, kann die Normalverteilung der Wahrscheinlichkeitsverteilung nach dem zentralen Grenzwerttheorem angenommen werden.

table (WPStudis$F19_Partnerschaft)
## 
## Nein   JA 
##   39   52

Varianzhomogenität

Wir haben schon verschiedene Methoden kennengelernt, Mittelwerte und Varianzen grafisch zu vergleichen. Zum Beispiel mit Boxplots.

boxplot(F21_01_Zufriedenheit_Leben ~ F19_Partnerschaft, data=WPStudis)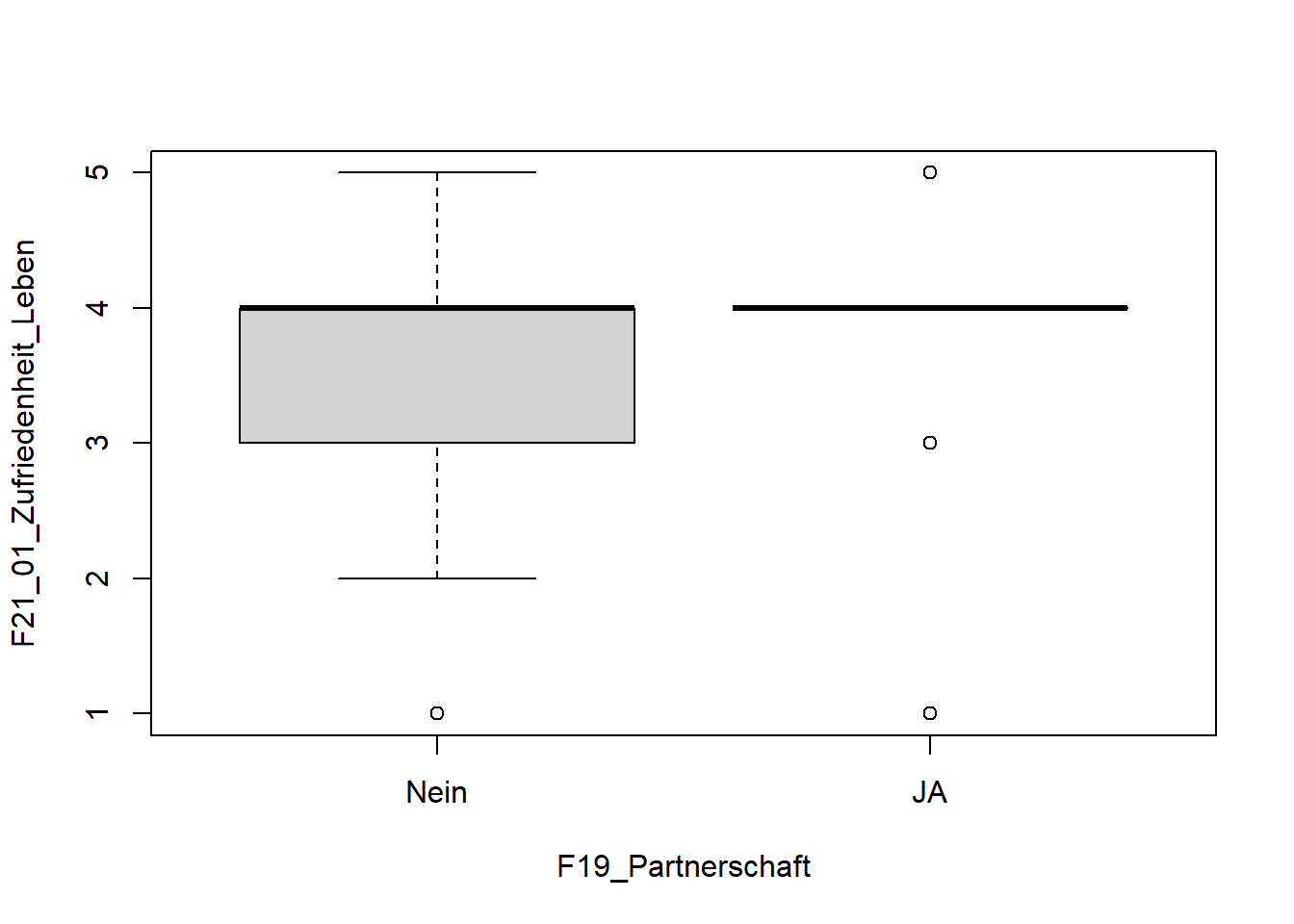

Besser als die grafische Analyse ist hier der Levene-Test als objektives Entscheidungskriterium für die Varianzhomogenität.

Hierzu nutzen wir die Funktion leveneTest() aus dem Paket car, welches wir natürlich zunächst laden müssen.

Die Notation entspricht dem t-Test: AV ~ UV (also Gruppe/Bedingung). Die Daten sollten dazu im “Long-Format” vorliegen. Bei Daten im “Wide-Format” müssen diese zunächst mit der Stack Funktion transformiert werden. Beim Levene-Test wird auf Varianzhomogenität geprueft und das Ergebnis sollte nicht signifikant werden. Wenn das Ergebnis signifikant wird, dann sollte im nächsten Schritt ein t-Test mit sogenannter Welch-Korrektur durchgeführt werden.

Führen wir nun den Test für unser Beispiel durch.

library(car)
leveneTest(F21_01_Zufriedenheit_Leben ~ F19_Partnerschaft, data=WPStudis) 
## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value  Pr(>F)  
## group  1  4.2869 0.04137 *
##       87                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Auf dem üblichen Signifikanzniveau von 0,05 wird der Levene-Test hier signifikant. Wir müssen also im Folgenden darauf achten, dass wir den t-Test durchführen, der keine Varianzhomogenität voraussetzt (Welch-Korrektur).

t-Test durchführen

Hinweis: var.equal=FALSE (also die korrigierte Version) ist die Voreinstellung – d. h. wir brauchen keinen zusätzlichen Befehl. Wenn Varianzhomogenität vorliegt, kann der klassische t-Test mit dem Argument var.equal=TRUE angefordert werden.

t.test(F21_01_Zufriedenheit_Leben ~ F19_Partnerschaft, data=WPStudis) 
## 
##  Welch Two Sample t-test
## 
## data:  F21_01_Zufriedenheit_Leben by F19_Partnerschaft
## t = -1.889, df = 64.311, p-value = 0.0634
## alternative hypothesis: true difference in means between group Nein and group JA is not equal to 0
## 95 percent confidence interval:
##  -0.66246744  0.01850459
## sample estimates:
## mean in group Nein   mean in group JA 
##           3.736842           4.058824

Wir erhalten einen t-Wert von -1.889 bei 64,3 Freiheitsgraden. Die ungeraden Freiheitsgrade entstehen dabei durch die Welch-Korrektur. Der p-Wert liegt bei 0.06 und wir können daher beim üblichen Signifikanzniveau von 0.05 die Nullhypothese nicht ablehnen. Der Test wird nicht signifikant und wir können also nicht sagen, dass sich Studierende, die Single sind und solche, die in Partnerschaft leben, hinsichtlich ihrer Lebenszufriedenheit unterscheiden.

Effektstärke berechnen

In diesem Beispiel wird der Test nicht signifikant, daher würden wir hier auch keine Effektstärke berechnen. Grundsätzlich ist die Berechnung der Effektgröße nach einem t-Test jedoch wichtig, weil sie eine Schätzung der Größe des Unterschieds zwischen den Mittelwerten zweier Gruppen liefert und es Ihnen ermöglicht, die Ergebnisse des t-Tests in den Kontext der praktischen Bedeutung des Unterschieds zu stellen.

Effektgrößenmaße wie Cohen’s d können nach einem t-Test berechnet werden, um Ihnen eine Vorstellung von der Größe des Unterschieds zwischen den Mittelwerten der verglichenen Gruppen zu geben. Eine kleine Effektgröße kann beispielsweise darauf hindeuten, dass der t-Test zwar einen statistisch signifikanten Unterschied zwischen den Gruppen gefunden hat, der Unterschied jedoch praktisch nicht signifikant ist. Andererseits kann eine große Effektgröße darauf hinweisen, dass der Unterschied zwischen den Gruppen sowohl statistisch signifikant als auch praktisch bedeutsam ist.

Effektgroesse Cohens d

Am einfachsten kann die Effektstärke Cohens d mit dem Paket effsize und die Funktion cohen.d() bestimmt werden.

Da es die Funktion cohen.d() auch im Paket psych gibt bestimmen wir hier mit “effsize::” welches Paket genutzt werden soll.

library(effsize)
## 
## Attache Paket: 'effsize'
## Das folgende Objekt ist maskiert 'package:psych':
## 
##     cohen.d
effsize::cohen.d(d = WPStudis$F21_01_Zufriedenheit_Leben, f = WPStudis$F19_Partnerschaft, na.rm=TRUE)
## 
## Cohen's d
## 
## d estimate: -0.4239098 (small)
## 95 percent confidence interval:
##       lower       upper 
## -0.85450654  0.00668704

Hierbei gibt d die abhängige Variable und f die unabhängige Variable oder gruppierungs Variable an.

Nach Cohen (1988) ergibt d = 0.2 einen kleinen Effekt, d=0.5 einen mittleren und ab d=0.8 einen starken Effekt. Wir haben hier also einen kleinen Effekt vorliegen.

Alternativ kann die Effektstärke auch mit dem Paket MBESS und der Funktion ci.smd ermittelt werden. Hierzu müssen Sie als Argumente die beiden Gruppengrößen eingeben.

library(MBESS)
ci.smd(ncp=t, n.1=39, n.2=52)
## $Lower.Conf.Limit.smd
## [1] -0.8379832
## 
## $smd
## [1] -0.4194227
## 
## $Upper.Conf.Limit.smd
## [1] 0.001442555

Effektgroesse r

Um die Effekt-Stärke ohne ein Package zu berechnen können wir einfach direkt die Formel der Effekt-groesse in R eingeben.

Die Formel lautet: r <- sqrt(t^2/(t2+df))

t<--1.98
df<-87
r <- sqrt(t^2/(t^2+df))
round(r, 3)
## [1] 0.208

Nach Cohen (1988) indiziert r = 0.1 einen kleinen Effekt, r=0.3 einen mittleren und r=0.5 einen starken Effekt (Entspricht dem Korrelationskoeffizienten r).

Die Effektstärke kann man übrigens auch einfacher berechnen,Sie entspricht der Punktbiserialen Korrelation, also der Pearson Korrelation zwischen den Variablen:

cor(WPStudis$F21_01_Zufriedenheit_Leben,as.numeric(WPStudis$F19_Partnerschaft), use="complete.obs", method="pearson")
## [1] 0.2074638

In diesem Video zeige ich wie das in R funktioniert:

Übung

Nutzen Sie hierfür die Daten “anorexia” (Magersucht) aus dem Package “MASS”.

library(MASS)
anorexia
##    Treat Prewt Postwt
## 1   Cont  80.7   80.2
## 2   Cont  89.4   80.1
## 3   Cont  91.8   86.4
## 4   Cont  74.0   86.3
## 5   Cont  78.1   76.1
## 6   Cont  88.3   78.1
## 7   Cont  87.3   75.1
## 8   Cont  75.1   86.7
## 9   Cont  80.6   73.5
## 10  Cont  78.4   84.6
## 11  Cont  77.6   77.4
## 12  Cont  88.7   79.5
## 13  Cont  81.3   89.6
## 14  Cont  78.1   81.4
## 15  Cont  70.5   81.8
## 16  Cont  77.3   77.3
## 17  Cont  85.2   84.2
## 18  Cont  86.0   75.4
## 19  Cont  84.1   79.5
## 20  Cont  79.7   73.0
## 21  Cont  85.5   88.3
## 22  Cont  84.4   84.7
## 23  Cont  79.6   81.4
## 24  Cont  77.5   81.2
## 25  Cont  72.3   88.2
## 26  Cont  89.0   78.8
## 27   CBT  80.5   82.2
## 28   CBT  84.9   85.6
## 29   CBT  81.5   81.4
## 30   CBT  82.6   81.9
## 31   CBT  79.9   76.4
## 32   CBT  88.7  103.6
## 33   CBT  94.9   98.4
## 34   CBT  76.3   93.4
## 35   CBT  81.0   73.4
## 36   CBT  80.5   82.1
## 37   CBT  85.0   96.7
## 38   CBT  89.2   95.3
## 39   CBT  81.3   82.4
## 40   CBT  76.5   72.5
## 41   CBT  70.0   90.9
## 42   CBT  80.4   71.3
## 43   CBT  83.3   85.4
## 44   CBT  83.0   81.6
## 45   CBT  87.7   89.1
## 46   CBT  84.2   83.9
## 47   CBT  86.4   82.7
## 48   CBT  76.5   75.7
## 49   CBT  80.2   82.6
## 50   CBT  87.8  100.4
## 51   CBT  83.3   85.2
## 52   CBT  79.7   83.6
## 53   CBT  84.5   84.6
## 54   CBT  80.8   96.2
## 55   CBT  87.4   86.7
## 56    FT  83.8   95.2
## 57    FT  83.3   94.3
## 58    FT  86.0   91.5
## 59    FT  82.5   91.9
## 60    FT  86.7  100.3
## 61    FT  79.6   76.7
## 62    FT  76.9   76.8
## 63    FT  94.2  101.6
## 64    FT  73.4   94.9
## 65    FT  80.5   75.2
## 66    FT  81.6   77.8
## 67    FT  82.1   95.5
## 68    FT  77.6   90.7
## 69    FT  83.5   92.5
## 70    FT  89.9   93.8
## 71    FT  86.0   91.7
## 72    FT  87.3   98.0

In Spalte “Treat” wird angegeben, ob die Person der Kontrollgruppe “Cont”, der Gruppe mit Cognitive Behavioural Treatment “CBT” oder der Gruppe mit Familiy Treatment “FT” angehört. Aufgabe: Ermitteln Sie, ob das Cognitive Behavioural Treatment im Vergleich zur Kontrollgruppe einen Effekt zeigt.

Die dritte Gruppe können wir aus den Daten löschen:

anorexia_two <- anorexia[anorexia$Treat=="CBT" | anorexia$Treat=="Cont",]
anorexia_two$Treat<-factor(anorexia_two$Treat)

Hinweis: Nutzen Sie hierzu die Gewichtsdifferenz. Diese müssen Sie berechnen.

Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.

t-Test für abhängige Stichproben

Ein t-Test fuer abhängige Stichproben (auch abhängiger t-Test) ist ein statistischer Test zum Vergleich der Mittelwerte von zwei abhängigen Stichproben. Eine abhängige Stichprobe bedeutet meist, dass die gleichen Personen mehrmals gefragt oder getestet werden (sog. Messwiederholungs-Design). Der Test wird verwendet, wenn Sie wissen möchten, ob die Mittelwerte zweier abhängiger Gruppen bzw. zweier Messzeitpunkte unterschiedlich sind. Sie könnten beispielsweise einen gepaarten t-Test verwenden, um festzustellen, ob der Mittelwertunterschied beim Blutdruck zwischen zwei Patientengruppen vor und nach einer Behandlung statistisch signifikant ist.

Um einen gepaarten t-Test in R durchzuführen, können Sie die Funktion t.test() verwenden. Die grundlegende Syntax ist identisch mit dem unabhängigen t-Test, nur dass zusätzlich das Argument paired=TRUE verwendet wird.

Übung

Sie wollen die Wirksamkeit einer neuen Wunderpille zur Steigerung der Trinkfestigkeit überprüfen.

Diese Pille gibt es übrigens wirklich. In folgendem Video gibt es mehr Informationen zu der Wunderpille und wie diese wirklich klinisch getestet wurden. Die folgenden Daten sind jedoch frei erfunden.

Sie entsenden eine Gruppe von 10 Personen an zwei Abenden auf den Stuttgarter Wasen und messen jeweils die getrunkene Menge Bier in Millilitern. Beim ersten Besuch erhalten 5 Personen die Pille und 5 nicht. Beim zweiten Besuch erhalten jeweils die anderen 5 die Pille.

Daten einlesen:

Wunderpille<-read.csv2(file="Wunderpille.csv")

Achtung, wenn die Daten der Gruppen in zwei unterschiedlichen Spalten vorliegt (wide-Format), ist die Notation des t-Tests: t.test(gruppe1, gruppe2, paired=TRUE)

Frage 1: Warum ist dieses Versuchsdesign besser als ein Test mit unabhängigen Gruppen?

Frage 2: Führen Sie einen t-Test durch, um die Frage zu beantworten, ob die Pille einen Effekt hat (Schritte von oben beachten)

Frage 3: Wie wäre das Ergebnis, wenn wir gerichtet getestet hätten (Wir gehen davon aus, dass die Pille wirkt)?

Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.

Ermittlung der notwendigen Stichprobengröße bei t-Tests

Nehmen wir an, Sie haben ein fiebersenkendes Medikament entwickelt. Dieses senkt das Fieber in ersten (Selbst-?)Versuchen um 2°Celsius. Die gepoolte Standardabweichung der Körpertemperatur beträgt 1,6°C. Die erwartete Effektgröße ist also ein Cohens d = 1,25 (Berechnung 2/1,6 = 1,25)

Wie viele Probanden brauchen Sie für einen klinischen Test mit zwei Stichproben (Kontrollgruppe und Experimentalgruppe) bei einem Signifikanzniveau von 5 %?

Hierfür nutzen wir den Power-Test pwr.t.test aus dem Paket pwr. Diese wird verwendet, um eine Power-Analyse für einen t-Test durchzuführen. Die Power-Analyse ist eine statistische Methode zur Bestimmung des Stichprobenumfangs, der erforderlich ist, um einen statistisch signifikanten Unterschied zwischen zwei Gruppen mit einem bestimmten Vertrauensniveau festzustellen. Sie hilft dabei, die Wahrscheinlichkeit zu bestimmen, dass eine Studie einen echten Unterschied einer bestimmten Größenordnung zwischen zwei Gruppen aufdeckt, falls dieser tatsächlich existiert.

Die grundlegende Syntax für die Funktion pwr.t.test() lautet:

pwr.t.test(d = effect_size, sig.level = significance_level, power = desired_power, type = “two.sample”, alternative = “two.sided”)

Wobei gilt

• d: ist die Effektgröße, die ein Maß für die Größe des Unterschieds zwischen den Mittelwerten der beiden Gruppen ist.
• sig.level: ist das Signifikanzniveau, das in der Regel auf 0,05 festgelegt ist.
• Power: ist die gewünschte Teststärke, die in der Regel auf 0,80 festgelegt ist.
  Typ: ist der Testtyp, eingestellt auf “zwei.Stichproben” für einen t-Test mit zwei Stichproben.
  Alternative: ist die Alternativhypothese, die auf “zweiseitig” oder “größer” oder “kleiner” eingestellt wird.

Hier nun mit unseren Zahlen.

library(pwr)
pwr.t.test(d=1.25,sig.level=0.05,power=0.8, type="two.sample",alternative="two.sided")
## 
##      Two-sample t test power calculation 
## 
##               n = 11.0942
##               d = 1.25
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

Für den klinischen Test sollten beide Gruppen mehr als 11 Personen groß sein.

Randbemerkung: Die Teststärke von 0.8 bedeutet, dass wir mit einem Beta-Fehler von 20 % leben können. Gerade in der klinischen Forschung ist dies jedoch ein sehr kritischer Wert (z. B. wenn es darum geht, ein neues Medikament zu finden).

In diesem Video zeige ich, wie das in R funktioniert:

Übung

Nehmen wir an Sie wissen, dass das Medikament das Fieber nur um 0,2 Grad senkt (und damit praktisch wirkungslos ist). Könnten Sie dennoch einen signifikanten klinischen Test erreichen? Was müssten Sie tun?

Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.

Ermittlung von kritischen Werten und p-Werten

Um zu einem Wert einer bekannten Verteilung (z,t,chi-quadrat) den zugehörigen p-Wert manuell zu ermitteln, gehen wir wie folgt vor:

Nehmen wir beispielhaft an, wir wollen in einem zweiseitigen t-Test mit 35 Freiheitsgraden den kritischen t-Wert bei einem Signifikanzniveau von 5 % ermitteln:

qt(0.025,35)
## [1] -2.030108
qt(0.975,35)
## [1] 2.030108

Wir können in R auch sehr einfach direkt den empirischen p-Wert bestimmen. Hierfür nutzen wir den Befehl pt und setzen den jeweiligen gefundenen empirischen t-Wert ein.

pt(-2,35)
## [1] 0.02665383

Übung

Ermitteln Sie den kritischen t-Wert für einen einseitigen t-Test mit einem Signifikanzniveau von 1 % und 120 Freiheitsgraden

Berechnen Sie den p-Wert für einen t-Wert von -2 bei 4 Freiheitsgraden.

Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.

Alternative zum t-Test: Bayes Factor Analysis

Wir wiederholen unsere Analyse zur Wunderpille (Messwiederholung) mit einem bayesischen Verfahren – Dem sog. Bayes Factor. Der Bayes Factor (BF) drückt das Verhältnis der Wahrscheinlichkeit der Alternativhypothese zur Wahrscheinlichkeit der Nullhypothese aus. Ein BF>1 sagt aus, dass die Daten unter Annahme der H1 wahrscheinlicher sind. Ein BF<1 sagt aus, dass die Daten unter Annahme der H0 wahrscheinlicher sind.
Ein BF von 4 sagt z. B. aus, dass das beobachtete Ergebnis 4-mal wahrscheinlicher unter Annahme der H1 ist als unter Annahme der H0. Größter Vorteil des BF im Vergleich zum p-Wert: Die Stichprobengroesse verfälscht hier das Ergebnis nicht!

library(BayesFactor)

Wir nutzen die Funktion ttestBF() mit x = Werte am ersten Messpunkt und y = Werte am zweiten Messpunkt -> Diese müssen also im Wide-Format vorliegen.

WP_wide<-unstack(Wunderpille)  #Bringt die Daten in das Wide Format

ttestBF(x = WP_wide$mit.Pille, y = WP_wide$ohne.Pille, paired=TRUE, rscale="wide") 
## Bayes factor analysis
## --------------
## [1] Alt., r=1 : 19.88331 ±0%
## 
## Against denominator:
##   Null, mu = 0 
## ---
## Bayes factor type: BFoneSample, JZS

Paired=True gibt an, dass es sich um ein Messwiederholungsdesign handelt (Funktion kann auch für unabhängige Daten verwendet werden)
rscale=“wide”gibt an, dass die Funktion die Effektstärke der Alternativhypothese nicht korrigiert (default ist eine Korrektur auf 0.7 Standardabweichungen)

Interpretation: Die beobachteten Ergebnisse sind rund 20-mal wahrscheinlicher unter der H1 (Pille wirkt) als unter der H0 (Pille wirkt nicht)