Zusammenhänge und Vorhersagen
5 Regression
5.0 Einführung
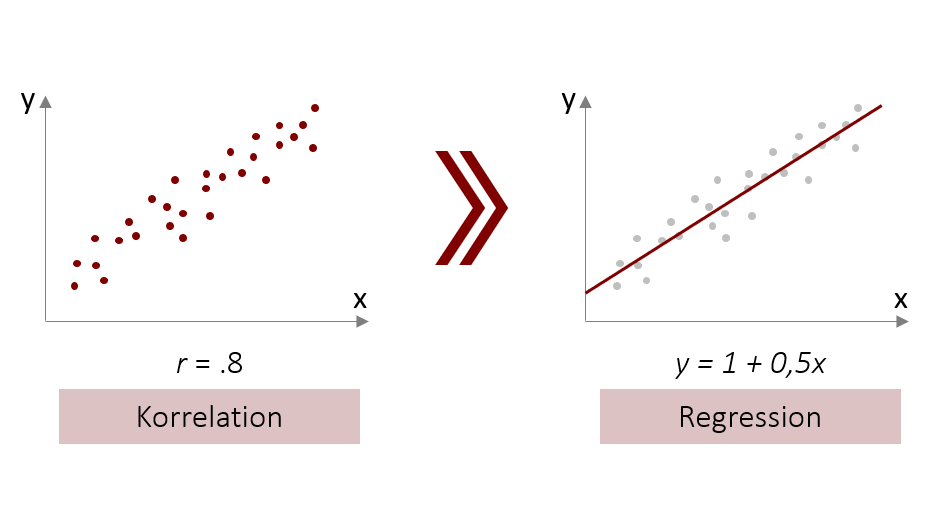
5.1 Die Regressionsgleichung
Wie wir schon im Kapitel 1 besprochen haben, wird die Vorhersagevariable als unabhängige Variable (UV) oder Prädiktorvariable bezeichnet; die Variable, die vorhergesagt werden soll, als abhängige Variable (AV) oder Kriteriumsvariable. Im Folgenden werden wir uns mit der Regressionsgleichung der bivariaten Regression beschäftigen, also für den Fall mit genau einer Vorhersagevariable und einer abhängigen Variable. Es gibt jedoch auch eine multiple Regression (mit mehreren Prädiktoren), die Sie später kennenlernen werden. Wir beschäftigen uns an dieser Stelle auch nur mit der gängigsten Form der Regression, der sogenannten linearen Regression. Diese ermöglicht eine Vorhersage unter der Annahme, dass es einen linearen, also gradlinigen Zusammenhang zwischen den Variablen gibt (Vgl. lineare Korrelation). Die Vorhersagefunktion sieht daher auch sehr einfach aus: Alle Vorhersagewerte liegen auf einer Geraden. Die Funktionsgleichung, die eine Gerade im zweidimensionalen Raum beschreibt kennen Sie sicherlich schon aus der Schulzeit. Dort wird diese meist mit f(x)= m ⋅ x +b beschrieben. Wobei m die Steigung ausdrückt und b den Y-Achsenabschnitt (oder Ordinatenabschnitt). Die Regressionsgleichung ist nichts anderes als diese lineare Funktion angewendet auf zwei Variablen. Jedoch sind in der Statistik andere Abkürzungen üblich. Der Y-Achsenabschnitt wird mit a bezeichnet, die Steigung wird mit b bezeichnet, und Regressionskoeffizient genannt.
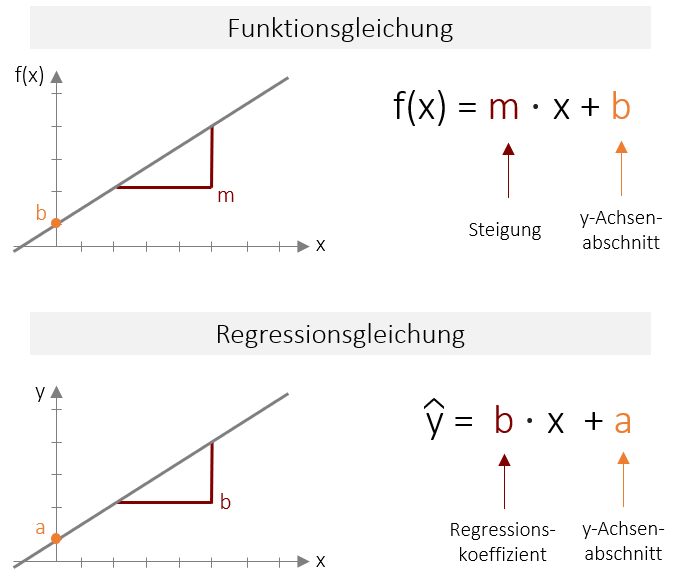
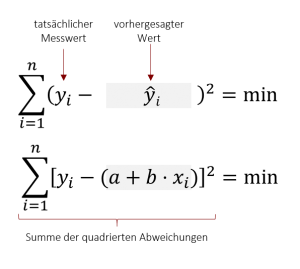
Die Funktion soll in Abhängigkeit des Prädiktors x, das Kriterium y vorhersagen (Daher steht vorne y). Da es sich hierbei um eine Schätzung handelt, die immer fehlerbehaftet ist, wird noch ein Fehlerterm (z.B. ε) eingefügt. Alternativ zu diesem Fehlerterm wird jedoch meist das y mit einem „Dach“ versehen, was in der Statistik ausdrückt, dass es sich um eine Schätzung handelt. Der Fehlerterm kann somit entfallen. In Summe lautet die Regressionsgleichung also:
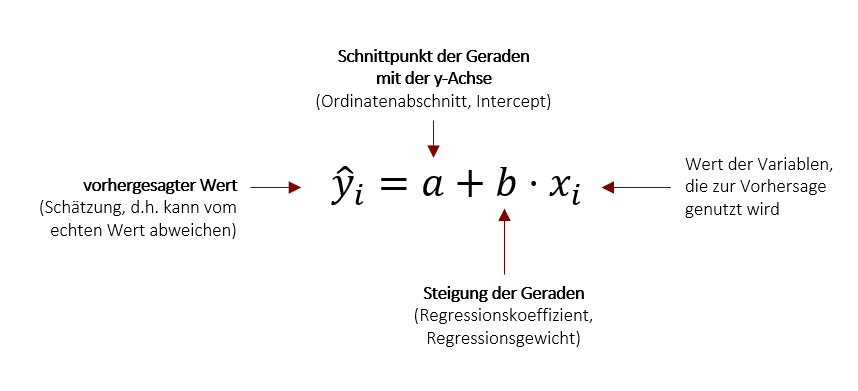
Der Index i drückt aus, dass Sie mit dieser Gleichung beliebige Werte der einen Variable für die Vorhersage des dazu gehörigen Werts der anderen Variable nutzen können. Im Falle des Eingangsbeispiels mit Körpergröße und Schuhgröße bedeutet dies, dass wir die Schuhgröße einer Person i vorhersagen bzw. schätzen können, wenn wir die die Körpergröße eben dieser Person i kennen.
Beispiel Regressionsgleichung
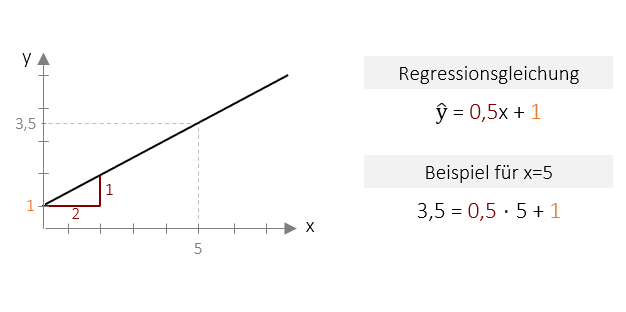
Unten abgebildet sehen Sie beispielhaft die grafische Darstellung einer Regressionsgleichung als Linie. Die Gleichung Y=0,5x + 1 beschreibt diese Linie eindeutig im zweidimensionalen Raum. Der Achsenabschnitt beträgt 1, was bedeutet das die Gerade genau beim Wert 1 die Y-Achse scheidet. Die Steigung beträgt 0,5, d.h. für jeweils eine „Schritt“ auf der X-Achse, geht es nur einen halbe „Schritt“ nach oben. Alle Vorhersage-Werte liegen genau auf dieser Geraden. So würden wir z.B. für den x-Wert 5 den y-Wert 3,5 vorhersagen. Dieser Wert lässt sich einfach durch Einsetzen in die Regression errechnen: Y= 0,5 ⋅ 5 + 1 . Wir können nun also für beliebige x-Werte die korrespondierenden y-Werte vorhersagen.
Video 5.1 Regression | Regressionsgleichung
5.2 Methode der kleinsten Quadrate
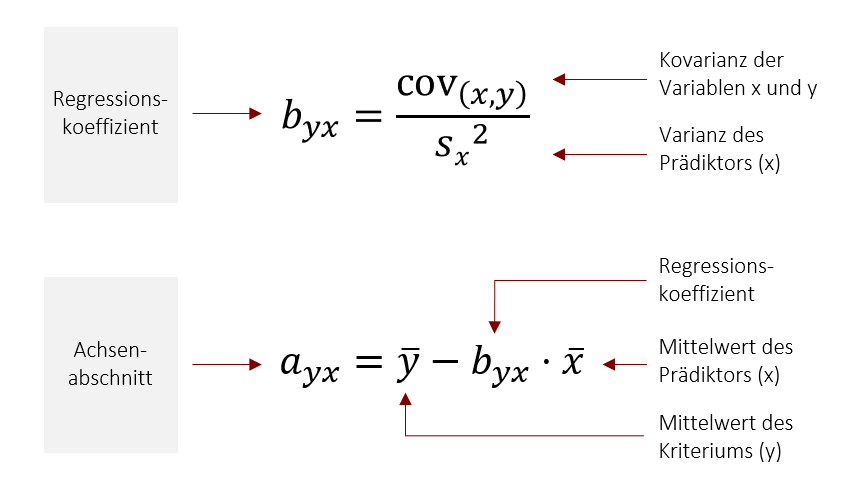
Bei byx und ayx bezeichnet der erste Index (hier: y) die Variable, die vorhergesagt wird (Kriterium) und der zweite Index die Variable, die vorhersagt (Prädiktor – hier: x). Um den Regressionskoeffizient b (die Steigung der Geraden) zu bestimmen, benötigen Sie also die Kovarianz der beiden Variablen, sowie die Varianz des Prädiktors (x) . Danach können Sie durch die einfache Multiplikation mit dem Mittelwert des Prädiktors (x) den Achsenabschnitt a bestimmen.
In der Praxis werden Sie eher selten eine Regressionsgleichung von Hand bestimmen. Dennoch ist es hilfreich zu verstehen, wie diese Gerade berechnet wird, da dieses sogenannte Generelle Lineare Modell (GLM) die Basis für fast alle späteren statistischen Verfahren bildet.
5.3 Vorhersagen
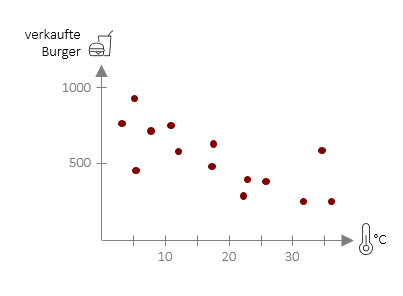
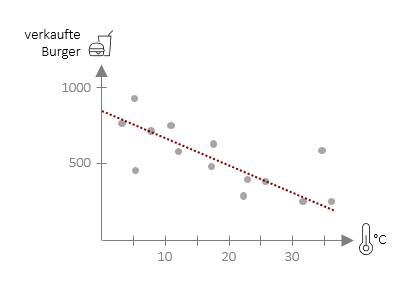
Die Regressionsgleichung kann ganz praktisch dazu verwendet werden konkrete Vorhersagen zu machen. Für die Vorhersage von Burgerverkäufen in einer unserer FiveProfs-Filialen auf Basis der Tagestemperatur lautet die Gleichung ![]() = 775 – 13,75 ⋅ xi . Hiermit können wir nun für eine beliebige Tagestemperatur die Burgerverkäufe in unserer Filiale vorhersagen. Wenn wir z.B. eine Temperatur von 20°C einsetzen, erhalten wir einen Vorhersagewert von 500 Burgern, die in unserer Filiale verkauft werden (Berechnung: 775 – 13,75 ⋅ 20).
= 775 – 13,75 ⋅ xi . Hiermit können wir nun für eine beliebige Tagestemperatur die Burgerverkäufe in unserer Filiale vorhersagen. Wenn wir z.B. eine Temperatur von 20°C einsetzen, erhalten wir einen Vorhersagewert von 500 Burgern, die in unserer Filiale verkauft werden (Berechnung: 775 – 13,75 ⋅ 20).
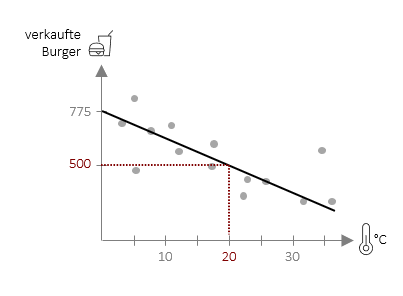
Die Vorhersage muss jedoch nicht zwangläufig mit der Realität übereinstimmen. In der Grafik ist deutlich erkennbar, dass viele Punkte leicht über oder unter der Vorhersagegeraden liegen – daher sprechen wir immer von einer Schätzung. Diese Schätzung kann verbessert werden in dem man mehr Daten aufnimmt, also die Gleichung auf Basis von mehr Tagen (bzw. in anderen Fällen: Personen) errechnet. Eine weitere Möglichkeit besteht darin, weitere Prädiktoren (wie hier z.B. die Regenwahrscheinlichkeit) mit aufzunehmen. Dazu werden wir an späterer Stelle kommen. Was wir jedoch schon jetzt benötigen, ist ein Maß dafür, wie gut unsere Schätzung ist und genau damit möchten wir uns – nach dem nächsten Beispiel – beschäftigen.
Beispiel Kreuzfahrtschiffe
In einer Stadt soll ein neuer Liegeplatz für Kreuzfahrtschiffe gebaut werden. Die maximal Breite der Schiffe, die die Hafeneinfahrt passieren können beträgt 35 Meter. Nun wollen Sie herausfinden, wie lang der geplante Liegeplatz werden sollte, damit er ein übliches Kreuzfahrtschiff aufnehmen kann. Wir wollen also auf Basis der Breite von 35 Metern (Prädiktor) die voraussichtliche Länge der Schiffe vorhersagen (Kriterium). Hierfür müssen Sie zunächst Daten von Kreuzfahrtschiffen sammeln. Grundsätzlich gilt: Je mehr Daten, desto besser die Vorhersage. In diesem Beispiel haben wir jedoch nur 11 Kreuzfahrtschiffe berücksichtigt. Im hier abgebildeten Streudiagramm ist bereits die Regressionsgerade eingezeichnet.
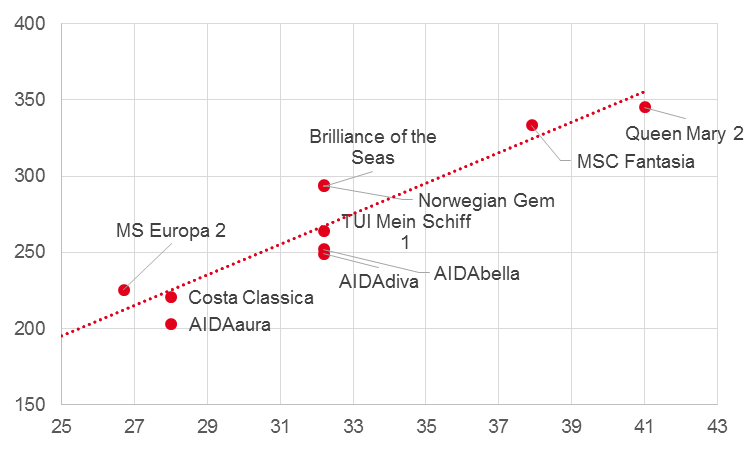
Wie man sieht gibt es einen (nicht-perfekten) Zusammenhang zwischen der Länge und der Breite der Kreuzfahrtschiffe. Um die Regressionsgerade zu bestimmen benötigen wir die Kovarianz der beiden Variablen cov(x,y) = 227,51, sowie die Varianz des Prädiktors s2x= 22,74. Hieraus können wir die Regressionsgleichung bestimmen:
![]() = -54,63 + 10 ⋅ xi
= -54,63 + 10 ⋅ xi
Mit dieser Gleichung können wir nun dem Planer der Hafenanlage helfen. Hierzu setzen wir für x=35 ein und erhalten ![]() = -54,63 + 10 ⋅ 35 = 295,37
= -54,63 + 10 ⋅ 35 = 295,37
Die vorhergesagte Länge für ein Kreuzfahrtschiff mit 35 Meter Breite beträgt also rund 295 Meter. Hierbei sollten sie jedoch beachten, dass es sich um eine Schätzung handelt, von der einzelne Kreuzfahrtschiffe in der Realität abweichen (siehe Abstände der Punkte von der Linie). Daher ist dem Hafenplaner gut daran geraten einen gewissen Sicherheitsaufschlag mit einzuplanen. Wie man bestimmen kann, wie genau eine solche Vorhersage ist, wollen wir im Folgenden betrachten.
5.4 Vorhersagegüte
Wir haben nun eine Methode entwickelt, mit der wir auf Basis von Daten Vorhersagen ableiten können. Wie wir gesehen haben, sind diese Vorhersagen jedoch nur Schätzungen und weichen manchmal mehr und manchmal weniger stark von der Realität ab. Wenn Sie die Folgenden zwei Streudiagramme betrachten, wird dies nochmal klarer: Beide haben eine lineare Regressionsgerade auf der die Vorhersagewerte liegen. Jedoch sind im Fall Burgerverkäufe und Tagestemperatur die echten Werte (rote Punkte) deutlich näher an der Geraden als in der rechten Grafik, in welcher die Burgerverkäufe auf Basis der Luftfeuchtigkeit vorausgesagt werden. Das bedeutet, dass die Vorhersage für die Burgerverkäufe mit der Tagestemperatur als Prädiktor deutlich besser funktioniert als mit der Luftfeuchtigkeit als Prädiktor.
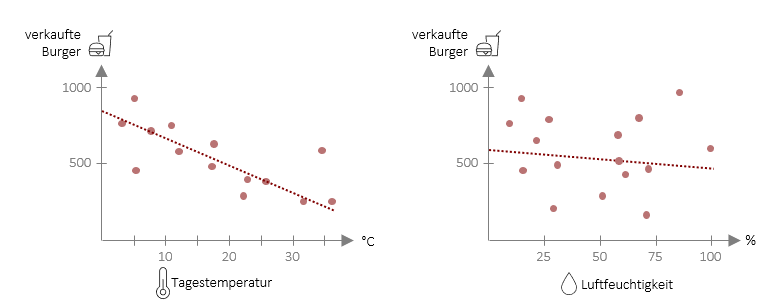
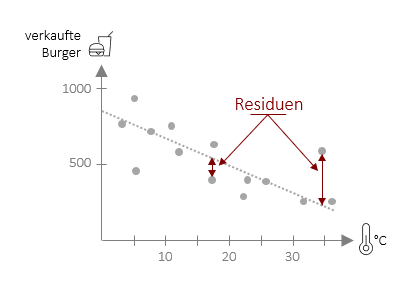
Wir können also über das Streudiagramm schon sehr leicht optisch sehen, wie gut eine Vorhersage funktioniert. Genau an dieser Stelle wollen wir nun weitermachen und Kennwerte entwickeln, die uns objektiv sagen, wie gut eine Vorhersage ist. Hierbei gehen wir zunächst genau so vor, dass wir die Abweichungen der echten Werte (auch beobachtete Werte) von der Geraden (vorhergesagte Werte) betrachten. Diese Abweichungen nennen sich Regressionsresiduen (y*i). Das Ausmaß der Abweichungen ist ein Indikator dafür, wie genau die Regression in ihrer Vorhersage ist. Die Regressionsresiduen selbst sind jedoch nur schwer interpretierbar, da diese wieder von der Skala der Variablen abhängen (Anzahl der verkauften Burger hat automatisch größere Residuuen als die Tagestemperatur in °C). Die Lösung: Wir setzen die Summe der Residuuen ins Verhältnis zu einem anderen Wert. Doch welchem?
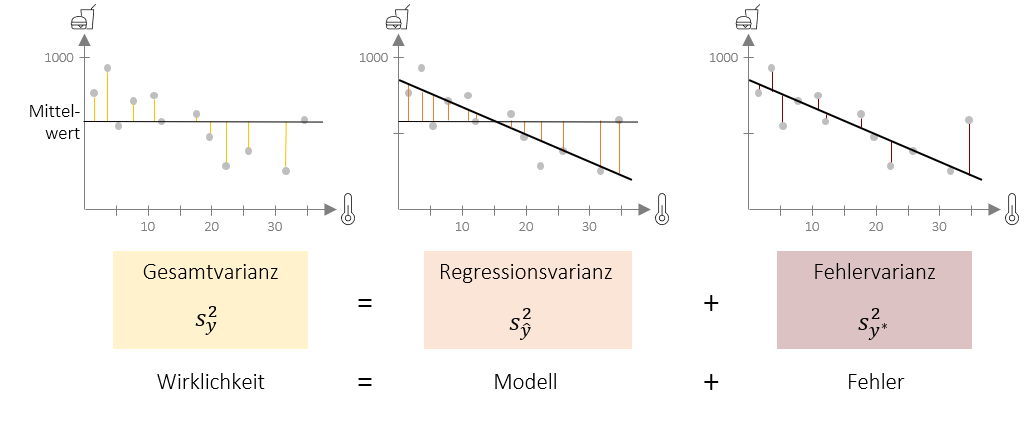
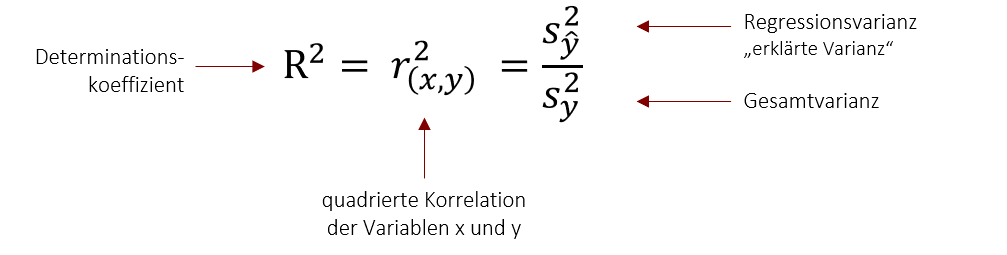
Hierfür wollen wir zunächst den Begriff der Varianz erweitern. Wir haben bisher gelernt, dass die Varianz die (quadrierte) Summe der Abweichung aller Werte von Mittelwert ist. Dies ist die im untenstehenden Bild links gezeigte Gesamtvarianz. Die Gesamtvarianz kann im Falle der Regression in zwei Komponenten geteilt werden: In die Regressionsvarianz und die Fehlervarianz. Die Regressionsvarianz drück aus, welche Abweichungen vom Mittelwert, das Regressionsmodell vorhersagt. Die Fehlervarianz drückt aus, wie die tatsächlichen Werte von dieser Vorhersage abweichen (daher nicht-erklärte Varianz). Hier nochmal in der Übersicht:
-
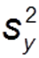 Gesamtvarianz: Quadrierte Abweichung aller Werte vom Mittelwert (unten gelb dargestellt)
Gesamtvarianz: Quadrierte Abweichung aller Werte vom Mittelwert (unten gelb dargestellt) -
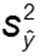 Regressionsvarianz (Auch erklärte Varianz): Quadrierte Abweichung der vorhergesagten Werte vom Mittelwert (unten orange dargestellt)
Regressionsvarianz (Auch erklärte Varianz): Quadrierte Abweichung der vorhergesagten Werte vom Mittelwert (unten orange dargestellt) 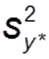 Fehlervarianz (Auch nicht-erklärte Varianz): Quadrierte Abweichung aller Werte von vorhergesagtem Wert (unten dunkelrot dargestellt)
Fehlervarianz (Auch nicht-erklärte Varianz): Quadrierte Abweichung aller Werte von vorhergesagtem Wert (unten dunkelrot dargestellt)
Video 5.4 Regression | Modellgüte
Grundsätzlich gilt, dass ein Regressionsmodell umso besser ist, je kleiner die Fehlervarianz im Vergleich zur vorhergesagten Varianz ist. Dies wird als F-Statistik bezeichnet und wird errechnet, in dem man die durch das Modell erklärte Varianz (Regressionsvarianz) ins Verhältnis zur nicht erklärten Varianz (Fehlervarianz) stellt. Dieser Quotient gibt damit an, um wie viel sich die Vorhersagegüte durch mein Modell verbessert, im Verhältnis zur noch nicht erklärten Varianz. Anders ausgedrückt zeigt dieser Wert an, ob sich durch das Regressionsmodell die Vorhersage verbessert im Vergleich zur Vorhersage nur durch den Mittelwert. Ein gutes Modell sollte daher immer mindestens einen F-Wert >1 haben.
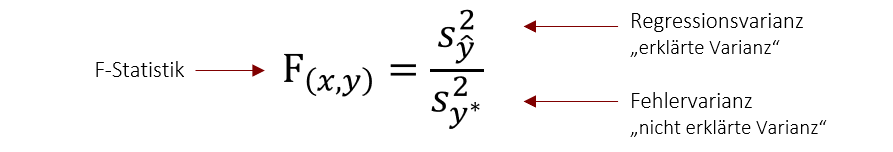
Beispiel Interpretation Regression und Gütemaße
Ein Dozent hat ein Regressionsmodell gebaut, welches die Note in der Statistik-Klausur vorhersagt und nutz dafür als Prädiktor die Anzahl der Stunden, die die Person jeweils auf die Klausur gelernt hat. Als Ergebnis erhält der Dozent folgende Regressionsgleichung:
![]() i= 4,5 + (-0,05 ⋅xi)
i= 4,5 + (-0,05 ⋅xi)
Zusätzlich erhält er folgende Gütemaße:
R2= 0,4 und F = 15
Zunächst können wir in diesem Fall die Regressionsgleichung auch inhaltlich interpretieren. Der Y-Achsenabschnitt a beträgt 4,5, was bedeutet, dass der Vorhersagewert für x=0 bei 4,5 liegt. Anders ausgedrückt: Ein Studierender, der 0 Stunden Vorbereitung für die Klausur investiert muss mit einer durchschnittlichen Note 4,5 rechnen (Nicht immer lässt sich der Y-Achsenabschnitt so sinnvoll interpretieren wie hier). Auch b lässt sich inhaltlich interpretieren. Pro Stunde Vorbereitungszeit sinkt die Note um 0,05. Das bedeutet zum Beispiel, dass das Model für eine Person mit 30h Vorbereitung, eine Note 3 vorhersagt.
Doch nun ist natürlich noch die Frage, wie gut diese Vorhersage ist. Der F-Wert liegt über 1 und wir können also sagen, dass das Modell eine Verbesserung der Vorhersage ermöglicht, im Vergleich zur Vorhersage durch den Mittelwert (wenn ich also für jeden Studierenden den Klassemittelwert als Vorhersagegröße nehmen würde). Der R2 Wert gibt weiter an , dass in diesem Fall 40% (0,4) der Varianz der abhängigen Variable durch die unabhängige Variable erklärt werden. Auf das Beispiel angewendet besagt dies, dass wir mit diesem Modell 40% der Schwankung in der Statistik-Klausurnote erklären können. Die übrigen 60% sind nicht aufgeklärte Varianz und werden also durch weitere (nicht im Modell vorhandene) Faktoren, wie z.B. Intelligenz beeinflusst.
Video 5.5 Regression | Determinationskoeffizient und F-Statistik
5.5 Voraussetzung für die lineare Regression
Um eine lineare Regression berechnen zu können, müssen eine Reihe von Voraussetzungen erfüllt sein. Diesen wollen wir uns nun kurz widmen:
- Der Prädiktor muss intervallskaliert sein. Ausnahme: dichotom nominalskalierte Variablen mit einer sogenannten Dummy-Codierung, also nur den Ausprägungen „0“ und „1“, können ebenfalls als Prädiktor genutzt werden
- Das Kriterium muss intervallskaliert sein. Für andere Skalenniveaus gibt es eigene Verfahren (z.B. ordinale, multinominale, logistische Regression)
- Der Zusammenhang der Variablen muss theoretisch linear sein. Hierfür hilft es das Streudiagramm zu betrachten. Für andere Zusammenhänge gibt es nicht-lineare Regressionsmodelle (z.B. quadratische Regression)
- Es sollten möglichst wenig Ausreiser in den Daten sein, da diese einen großen Einfluss auf die Vorhersagegüte haben können. Auch hier hilft es das Streudiagramm zu betrachten.
Expertenwissen: Regression in der Inferenzstatistik
Für die Anwendung der Regression in der Inferenzstatistik gibt es noch weitere Voraussetzungen, die wir später beim Thema der multiplen Regression vertiefen werden. Diese sind:
- Die Einzelwerte verschiedener Merkmalsträger müssen voneinander unabhängig zustande gekommen sein
- Residuen dürfen nicht korrelieren
- Die Residuen sollen normalverteilt sein
- Homoskedastizität: Streuungen der zu einem x-Wert gehörenden y-Werte müssen über den ganzen Wertebereich von x homogen sein
Video 5.6 Regression | Vorraussetzungen
5.6 Standardisierung der Regressionsgeraden
Wir können nun mehrere Regressionsmodelle im Hinblick auf die Vorhersagegüte vergleichen. Wollen wir jedoch den Regressionskoeffizienten b von mehreren Regressionsmodellen vergleichen, haben wir ein Problem: Das Gewicht b ist nicht unabhängig von der entsprechenden Skalierung zu interpretieren, d.h. Gewichte verschiedener Regressionsgleichungen können nicht miteinander verglichen werden. So führt zum Beispiel die Körpergröße in Zentimetern als Prädiktor zu einem größeren b als die Körpergröße in Metern. Daher spricht man auch oft vom unstandardisierten Regressionsgewicht b. Über Standardisierung an den Standardabweichungen werden die Gewichte miteinander vergleichbar. Der standardisierte Regressionskoeffizient 𝛽 (𝛽-Gewicht) ist im Falle der bivariaten Regression identisch mit der Produkt-Moment-Korrelation r, d.h. kann Werte zwischen -1 bis +1 annehmen. Die Standardisierung erfolgt wieder an den Standardabweichungen beider Variablen, wie folgt:
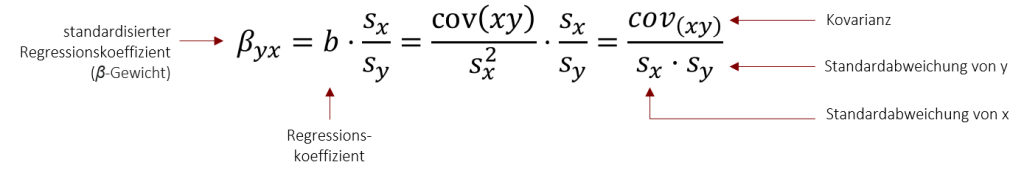
Das Ergebnis dieser Gleichung sollte Ihnen bekannt vorkommen. Es entspricht der Formel für die Produkt-Moment-Korrelation. Dies zeigt auf mathematischem Wege die Verwandtschaft von Korrelation und Regression.
Video 5.8 Regression | Standardisiertes Regressionmodell
Mit der Standardisierung lassen sich aber auch spannende Praxisprobleme lösen. Daher wollen wir uns im folgenden Kapitel mit einer besonders nützlichen Form der Standardisierung, der sog. Z-Transformation beschäftigen.
5.7 Regression mit SPSS
Regressionsmodelle lassen sich in SPSS mit wenigen Klicks erstellen, jedoch ist die Interpretation der Ausgabe nicht ganz einfach. Zur Erstellung eines Regressionsmodells gibt es in SPSS folgendes Menü:
Analysieren > Regression > Linear.
Hier wird zunächst die abhängige Variable eingetragen (Kriterium, also die Variable die wir vorhersagen wollen) und dann die unabhängige Variable (Prädiktor, die Variable, die wir zur Vorhersage nutzen). Das Menü bietet viele weitere Einstellung, die aber für ein einfaches Regressionsmodell nicht notwendig sind. Die resultierende Ausgabe gibt uns die Regressionskoeffizienten, also die Werte, die wir benötigen um die Regressionsgleichung aufzustellen. Überdies werden standardmäßig die Gütemaße R2 und F-Statistik mit ausgegeben, die es uns erlauben zu beurteilen, wie gut das Modell Vorhersagen macht. Im Folgenden Video wird dies Schritt für Schritt erklärt:
5.9 Regressionsmodelle mit SPSS erstellen
Wie in den vorigen Kapiteln besprochen setzt die Berechnung eines Regressionsmodells voraus, dass auch wirklich ein linearer Zusammenhang zwischen den Variablen besteht. Daher sollten zur Interpretation eines Regressionsmodell die Daten immer auch in grafischer Form mit Hilfe eines Streudiagramms betrachtete werden. In SPSS bieten Streudiagramme zudem auch die Möglichkeit, direkt eine Regressionsgrade einzuzeichnen, sowie die Regressionsgleichung und das Gütemaß R2 auszugeben. Wie dies funktioniert, wird im nächsten Video besprochen:
5.10 Streudiagramm mit Regressionsgerade in SPSS
5.7 Übungsfragen
Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!
In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!



