Hypothesentests
14 Vorzeichentest
14.0 Einführung Binomialverteilung
Stellen Sie sich vor, Sie möchten wissen, welcher Standort für Ihren Burgerladen besser ist und lassen hierzu eine Gruppe von potenziellen Kunden beide Orte bewerten. Oder Sie interessieren sich dafür, ob die Zufriedenheit Ihrer Kunden im Burgerladen steigt, nachdem Sie ihnen ein kostenloses Getränk anbieten. Solche Unterschiedshypothesen können wir mit einem Vorzeichentest testen, welcher auf der Binomialverteilung beruht. Die Binomialverteilung gehört zu den diskreten Wahrscheinlichkeitsverteilungen. Diese ordnen diskreten Zufallsvariablen, welche nur eine abzählbare Menge an Ausprägungen annehmen können, die entsprechenden Wahrscheinlichkeiten zu. Im Fall der Binomialverteilung wird eine dichotome Variable (auch Bernoulli-Variable) als Grundlage verwendet.
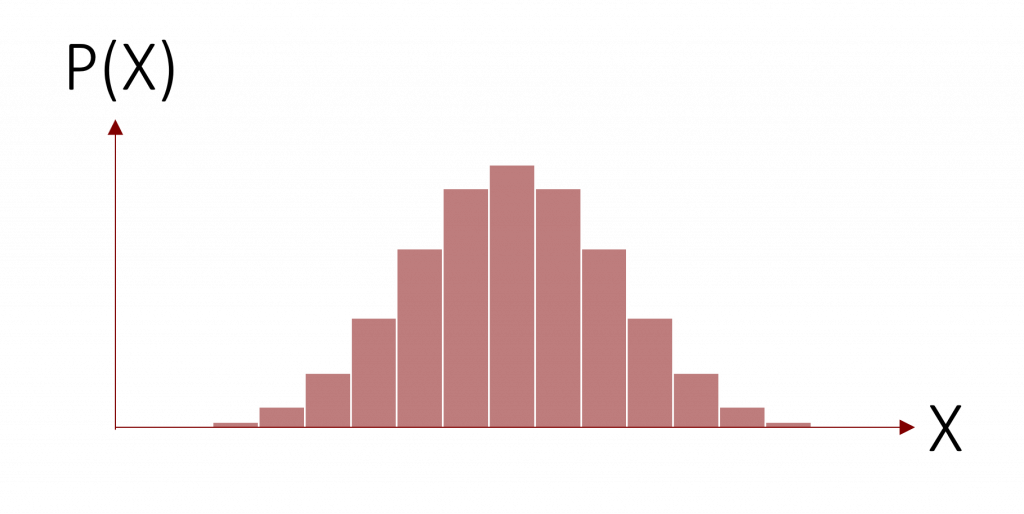
Sie kann genau zwei verschiedene Ausprägungen annehmen. Beispielweise Kopf/ Zahl, Erfolg/ Misserfolg, oder ganz Allgemein: Ereignis tritt ein/ Ereignis tritt nicht ein. Wiederholen wir einen Versuchsaufbau mit solch einer dichotomen Variable N-mal (man spricht auch von Bernoulli-Experiment), z.B. indem wir N = 5 eine Münze werfen, erhalten wir N + 1 (in unserem Fall 6) mögliche Ausgänge, wie oft wir Kopf geworfen haben könnten. Die zugehörige Binomialverteilung bildet nun die entsprechenden Wahrscheinlichkeiten für die einzelnen Ereignisse ab.
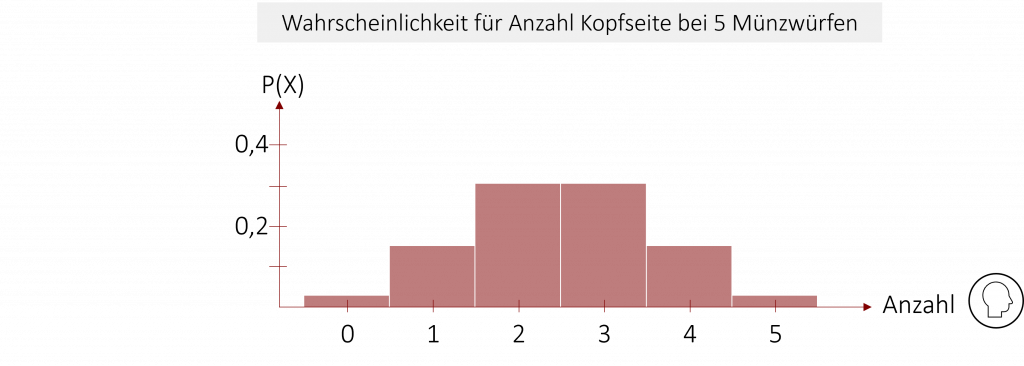
Wie auch schon bei der Normalverteilung, gibt es nicht die eine Binomialverteilung. Viel eher variiert ihre Gestalt abhängig von der Auftretenswahrscheinlichkeit π und der Anzahl der Ereignisse n + 1. Im Beispiel unseres Münzwurfs haben wir eine Auftretenswahrscheinlichkeit, dass wir Kopf werfen von π = 0,5. Dadurch ist unsere Binomialverteilung symmetrisch. Ist π < 0,5 ist die Verteilung hingegen linkssteil. Wird π > 0,5 wird die Binomialverteilung rechtssteil.
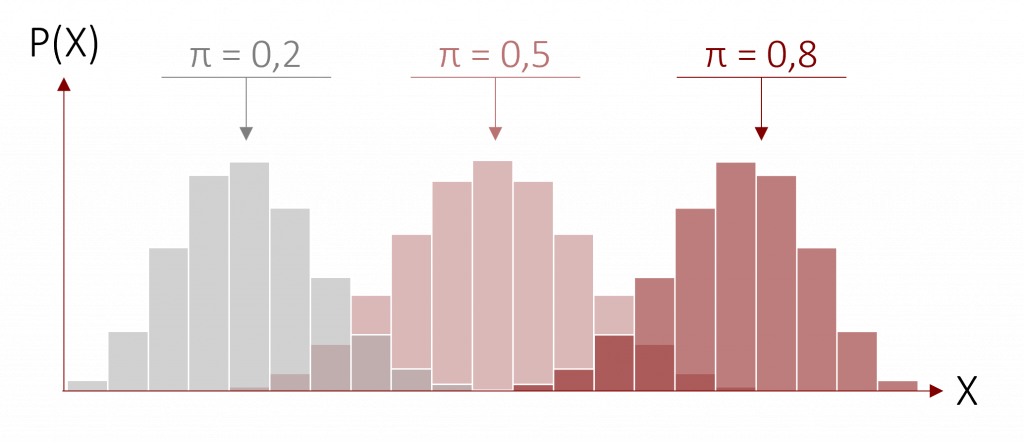
Je größer hierbei das n wird, desto eher kann man die Binomialverteilung in einer Normalverteilung approximieren (überführen). Die Approximation ist unabhängig der Auftretenswahrscheinlichkeit π.
Wenn Sie die Logik der Binomialverteilung nochmals anhand eines Beispiels aus der FiveProfs Kette nachvollziehen möchten, bietet Ihnen das folgende Video eine gute Gelegenheit.
18.1 Binomialverteilung | Einführung
Im Gegensatz zu stetigen Wahrscheinlichkeitsverteilungen, ist das Rechnen mit der diskreten Binomialverteilung deutlich einfacher. Wir müssen uns nicht mehr mit der Integralrechnung behelfen, sondern können die Wahrscheinlichkeiten für ein Ereignis direkt aus der Grafik oder der entsprechenden Tabelle (siehe Appendix) herauslesen.
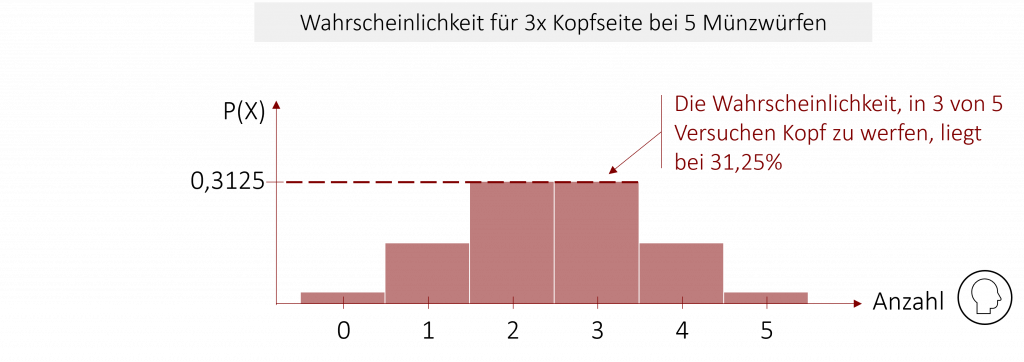
Wahrscheinlichkeit für das Auftreten eines Ereignisses bestimmen
Um die Wahrscheinlichkeit für das Auftreten eines bestimmten Ereignisses zu bestimmen, rechnen wir die Auftretenswahrscheinlichkeit π hoch die Anzahl der Ereignisse n.
P(X) = πn
Beispiel Münzwurf
Wir werfen 7-mal eine Münze. Wir wahrscheinlich ist es, dass wir 7-mal Kopf und damit 0-mal Zahl erhalten?
Antwort:
P(X=0) = πn = 0,57 = 0,0078
Die Wahrscheinlichkeit, dass wir 7-mal Kopf werfen, beträgt 0,78%.
Jedoch trifft diese Formel nur auf Ereignisse zu, die nur durch durch einen Fall entstehen können. Gibt es mehrere Möglichkeiten, wie ein Ereignis zustande kommen kann, so werden diese Möglichkeiten aufaddiert, wie das folgende Beispiel zeigt:
Beispiel Münzwurf
Wir werfen 7-mal eine Münze. Wie wahrscheinlich ist es das wir 1-mal Kopf erhalten?
Antwort:
Zunächst rechnen wir, die Wahrscheinlichkeit für ein konkretes Ereignis. Nämlich, dass wir 1 Mal in den 7 Malen Kopf werfen.
πn = 0,57 = 0,0078
Nun können wir aber ganz am Anfang Kopf werfen, oder in der Mitte oder ganz zum Schluss. Es gibt also verschiedene Fälle an denen wir zum Schluss 1-mal Kopf und 6-mal Zahl gewürfelt haben.
Um nun die Wahrscheinlichkeit zu berechnen, addieren wir die 7 Möglichkeiten auf und erhalten so eine Wahrscheinlichkeit von:
7 ⋅ πn = 7 ⋅ 0,57 = 7 ⋅ 0,0078 = 0,0546
Die Wahrscheinlichkeit, dass wir 1-mal Kopf werfen, beträgt 5,46%.
Wahrscheinlichkeit für einen Bereich bestimmen
Um die Wahrscheinlichkeit für einen Bereich zu bestimmen, addieren wir die entsprechenden Ereignisse einfach auf.
Beispiel Münzwurf
Wie wahrscheinlich ist es, dass wir 0-mal oder 1-mal Kopf werfen, wenn wir eine Münze 7-mal werfen?
Antwort:
P(X=0) + P(X=1) = P(X≤1)
P(X≤1) = 0,0078 + 0,0547 = 0,0625
Die Wahrscheinlichkeit, dass wir höchstens 1-mal Kopf werfen, beträgt 6,25%.
Das folgende Video bietet Ihnen weitere Beispiele anhand eines Gewinnspiels aus der FiveProfs-Kette.
18.2 Binomialverteilung | Rechenbeispiel
14.1 Der Vorzeichentest
Mit dem Vorzeichentest können zwei abhängige Merkmale auf Unterschiede getestet werden. Abhängig heißt hierbei, dass die Ausprägung der Merkmale von einander abhängen. Beispielsweise dadurch, dass ein und dieselbe Person zu zwei verschiedenen Merkmalen (z.B. Bewertung zwei verschiedener Burger) oder zu zwei verschiedenen Zeitpunkten befragt wird (z.B. Bewertung des selben Burgers vor und nach einem Softdrink), man spricht hier auch von einem Messwiederholungsdesign.
Die ungerichteten Hypothesen, die der Vorzeichentest dabei untersucht, lauten:
H0: Es gibt keinen Unterschied zwischen beiden Messwerten bzw. Ausprägungen.
H1: Es gibt einen Unterschied zwischen beiden Messwerten bzw. Ausprägungen.
Damit können eine Reihe an unterschiedlichen Hypothesen überprüft werden.
Beispiele für zu überprüfende Hypothesen
Hypothesenpaare für zwei unterschiedliche Messzeitpunkte:
H0: Der Burger schmeckt zu beiden Messzeitpunkten gleich.
H1: Der Burger schmeckt vor dem Softdrink süßer als nachher.
H0: Die Mitarbeitermotivation ist zu beiden Messzeitpunkten gleich.
H1: Die Mitarbeitermotivation ist nach dem Teamevent höher als zuvor.
Hypothesenpaare für zwei unterschiedliche Ausprägungen (die bei der selben Person erhoben wurden):
H0: Die Burger unterscheiden sich geschmacklich nicht voreinander.
H1: Burger A schmeckt besser als Burger B.
H0: Die Zufriedenheit mit der Sauberkeit im Empfangs- und Thekenbereich ist gleich.
H1: Die Zufriedenheit mit der Sauberkeit im Thekenbereich unterscheidet sich von der Zufriedenheit mit der Sauberkeit im Empfangsbereich.
Der Vorzeichentest berücksichtigt bei der Überprüfung der Unterschiede zwischen zwei Messwerten lediglich, ob einer der Werte besser oder schlechter ist. Jedoch nicht, um wie viel besser oder schlechter der eine Messwert im Gegensatz zum anderen Messwert abschneidet. Möchten wir auch diese Informationen bei unserer Analyse mit einbeziehen, sollten wir auf den t-Test für abhängige Stichproben zurückgreifen. Dieser hat jedoch höhere Voraussetzungen als der Vorzeichentest und wird im nächsten Kapitel behandelt.
Die Voraussetzungen des Vorzeichentests sind:
- mindestens Ordinaldaten
Nochmal zur Erinnerung: Die Ausprägungen von ordinalen Variablen lassen sich in eine klare Rangfolge bringen, jedoch kann man über die Abstände zwischen den einzelnen Ausprägungen keine Aussage treffen. - zwei abhängige Stichproben
Diese sind bei einem Messwiederholungsdesign gegeben. Hierzu wird entweder dieselbe (oder einer ähnliche) Person zu zwei verschiedenen Messzeitpunkten oder zu zwei verschiedenen Themen befragt. Die beiden Messwerte hängen somit voneinander ab.
Sind diese Voraussetzungen gegeben können wir mit der Berechnung der Teststatistik fortfahren. Falls Sie bis hierhin noch Fragen haben sollten, lohnt es sich das folgende Video der FiveProfs Kette anzuschauen.
18.3 Vorzeichentest | Einführung
14.2 Berechnung des Vorzeichentests
Um Ihnen die Berechnung des Vorzeichentests zu verdeutlichen, stellen Sie sich folgendes Szenario vor: Sie möchten die Motivation Ihrer Belegschaft in den FiveProfs-Filialen steigern. Dafür möchten Sie ein neues Outdoor-Event testen, welches die Teams zusammenschweißen soll. Um zu überprüfen, ob das Event auch wirklich den gewünschten Erfolg erzielt, führen Sie es mit Ihrer Stuttgarter Filiale durch und fragen die Motivation der Mitarbeitenden einmal vor und einmal nach dem Event ab. Hierzu müssen sie auf einer 5-stufigen Skala ihre Motivation angeben, wobei 5 für eine hohe und 1 für eine niedrige Motivation steht. Das sind die Ergebnisse:
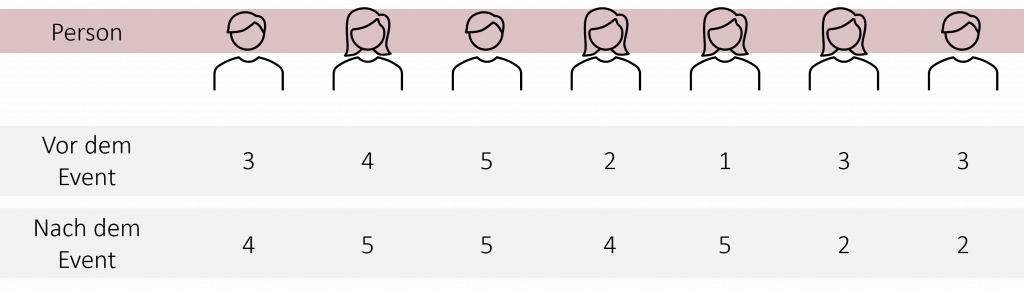
Unsere zu überprüfenden Hypothesen lauten wie folgt:
H0: Die Motivation der Mitarbeitenden ist nach dem Event gleich oder geringer als vorher.
H1: Die Motivation der Mitarbeitenden ist nach dem Event gestiegen.
Schritt 1: Bestimmung der Vorzeichen
Zunächst bestimmen wir für jeden Probanden, ob die Differenz zwischen den beiden Messwerten positiv oder negativ ist.
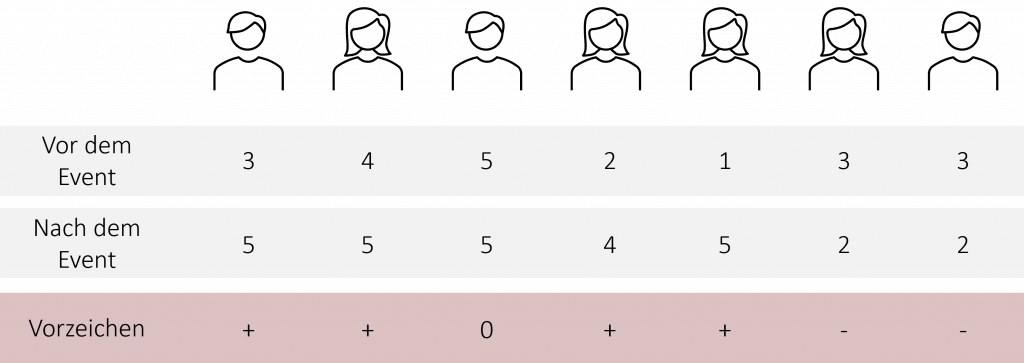
Wir sehen, dass die dritte Person keine Veränderung in seiner Motivation aufweist. Wenn zwei Ausprägungen von einer Person gleich bewertet werden, werden diese Messwerte beim Vorzeichentest nicht berücksichtigt. Dementsprechend fällt die dritte Person aus unserer Stichprobe raus. Die neue Datengrundlage besteht somit aus 6 Mitarbeitenden.
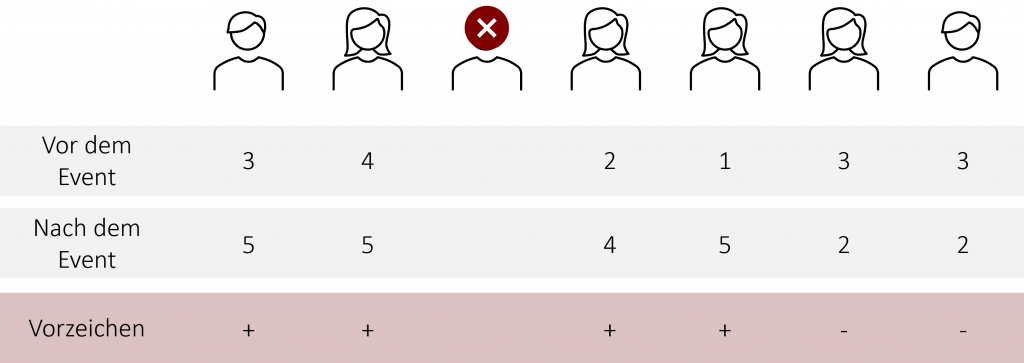
Schritt 2: Bestimmung der Wahrscheinlichkeit eines solchen Ereignisses
Nun bestimmen wir die Wahrscheinlichkeit, ein solches Ereignis zu erhalten unter der Annahme der Nullhypothese. Für unser Beispiel lautet die Frage also: Wie wahrscheinlich ist es, dass unsere Mitarbeitenden solche Ratings abgeben unter der Annahme, dass durch das Outdoor-Event die Motivation gleich bleibt oder sinkt?
Für die Beantwortung der Frage hilft uns die Binomialverteilung. In ihr können wir die Wahrscheinlichkeit für ein solches Ereignis direkt ablesen. Hierfür müssen wir nur wissen, welche Binomialverteilung zugrunde liegt. Ihre Erscheinung hängt, wie wir vorher schon besprochen haben, von der Auftretenswahrscheinlichkeit π und der Anzahl der Ereignisse n + 1 ab. Im Falle des Vorzeichentests ist die Auftretenswahrscheinlichkeit immer π = 0,5 und die Anzahl der Ereignisse ist die Stichprobengröße n + 1. In unserem Fall haben wir also einer Binomialverteilung mit n = 6 und π = 0,5.
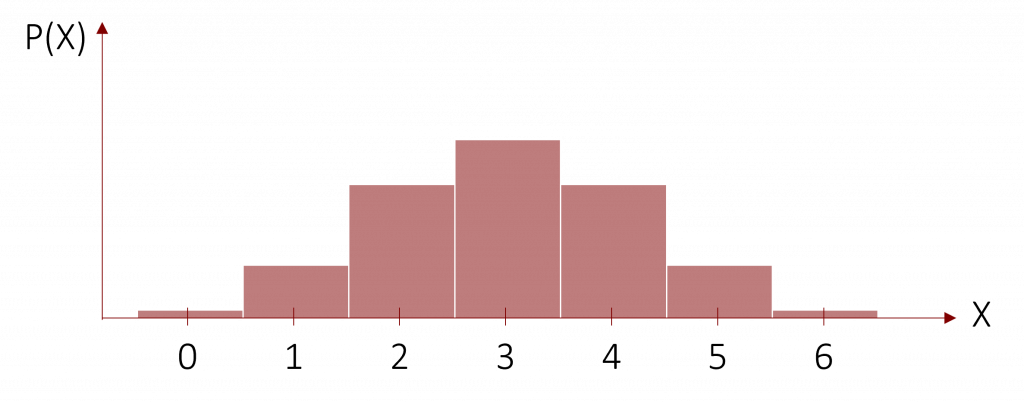
Zudem müssen wir wissen, welche Wahrscheinlichkeit wir ablesen (oder berechnen) müssen. Hierzu schauen wir uns an, welches Vorzeichen in geringerem Maße vertreten ist. In unserem Fall sind die negativen Vorzeichen nur 2-mal vertreten, weshalb wir diese bei der Berechnung unserer Wahrscheinlichkeit zugrunde legen. Wir berechnen nun die Wahrscheinlichkeit, dass ein solcher oder kleinerer Wert von 2 auftritt und rechnen hierzu die Wahrscheinlichkeiten für die Werte 0 bis 2 in der entsprechenden Binomialverteilung zusammen.
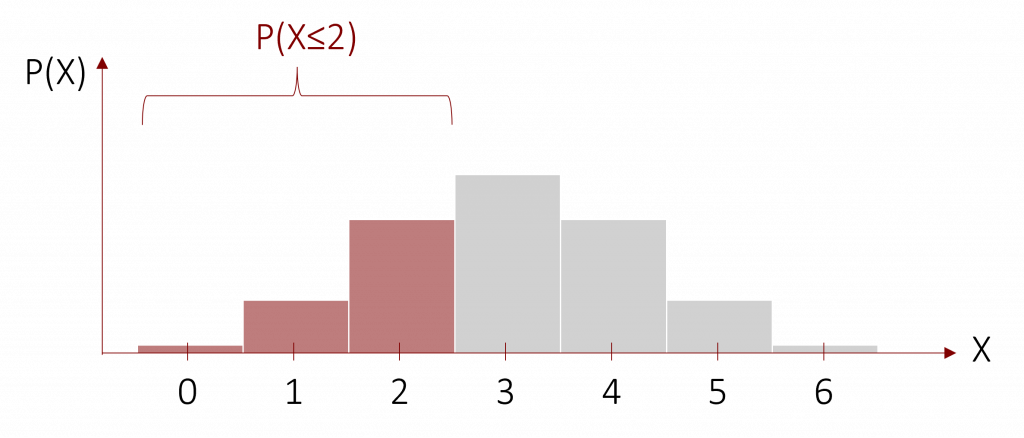
Die entsprechenden Werte finden Sie entweder in einer Tabelle, die die Wahrscheinlichkeiten der entsprechenden Binomialverteilung abbildet (siehe Appendix) oder Sie berechnen die entsprechenden Wahrscheinlichkeiten selbst, wie wir es bereits oben im Kapitel gemacht haben. In unserem Beispiel ergibt sich eine Wahrscheinlichkeit von P(X≤2) = 0,3437.
Ab einer Stichprobengröße von n ≥ 20 kann für die Berechnung der Wahrscheinlichkeit approximativ die Normalverteilung unterstellt werden. In diesen Fällen kann zusätzlich ein entsprechender Z-Wert berechnet werden, bevor dessen Wahrscheinlichkeit in der Tabelle der Normalverteilung abgelesen werden kann.
Schritt 3: Ablehnung oder Annahme der Nullhypothese
Um die Nullhypothese ablehnen zu können, muss die errechnete Wahrscheinlichkeit für das aufgetretene Ereignis unter dem im Vorhinein definierten Signifikanzniveau α liegen. Dieses Signifikanzniveau liegt üblicherweise bei 5% oder weniger. In unserem Beispiel müssen wir die Nullhypothese somit beibehalten, da die errechnete Wahrscheinlichkeit von 34,37% über einem Signifikanzniveau von α = 5% liegt.
Bei gerichteten Hypothesen muss zudem eine weitere Bedingung überprüft werden, um die Nullhypothese ablehnen zu können. Hierbei müssen zusätzlich die überwiegenden Vorzeichen mit der aufgestellten Alternativhypothese übereinstimmen. In unserem Fall heißt das, dass die positiven Vorzeichen überwiegen müssen (was mit 4 positiven und 2 negativen Vorzeichen in unserem Beispiel auch der Fall ist). Erst wenn beide Bedingungen bei der gerichteten Hypothese zutreffen, können wir die Nullhypothese ablehnen.
Die nachfolgende Tabelle zeigt nochmal eine Übersicht, wann wir die Nullhypothese ablehnen können:
| Hypothese | ungerichtet | gerichtet (X1 < X2) | gerichtet (X1 > X2) |
| Beispiel Alternativhypothese | Die Motivation der Mitarbeitenden verändert sich nach dem Outdoor-Event. | Die Motivation der Mitarbeitenden ist nach dem Outdoor-Event höher. | Die Motivation der Mitarbeitenden ist nach dem Outdoor-Event geringer. |
| H0 ablehnen, wenn | P(X) ≤ α/2 | P(X) ≤ α | P(X) ≤ α |
| mehr positive Vorzeichen als negative | mehr negative Vorzeichen als negative |
Zudem demonstriert Ihnen das folgende Video die Berechnung anhand eines Beispiels aus der FiveProfs Kette.
18.4 Vorzeichentest | Rechenbeispiel
14.3 Übungsfragen
Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!
In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!


