Statistik mit R & RStudio
25 Zweifaktorielle ANOVA mit R (TWO-Way Independent ANOVA)
Zweifaktorielle ANOVA (TWO-Way Independent ANOVA)
Eine zweifaktorielle ANOVA (Varianzanalyse) ist eine statistische Methode, mit der festgestellt werden kann, ob eine Wechselwirkung zwischen zwei unabhängigen Variablen und einer kontinuierlichen abhängigen Variablen besteht. Sie ist eine Erweiterung der einseitigen ANOVA, bei der die Mittelwerte von zwei unabhängigen Variablen mit einer abhängigen Variablen verglichen werden. Sie wird verwendet, um festzustellen, ob es eine Wechselwirkung zwischen den beiden unabhängigen Variablen gibt, was bedeutet, dass die Wirkung einer unabhängigen Variablen auf die abhängige Variable von der Höhe der anderen unabhängigen Variable abhängt.
Ein Beispiel: Ein Forscher möchte die Auswirkungen einer neuen Lehrmethode (x1) und des Geschlechts der Schüler (x2) auf die Schülerleistungen (y) untersuchen. Der Forscher teilt die Schüler nach dem Zufallsprinzip einer von drei Gruppen zu: einer Kontrollgruppe (traditionelle Lehrmethode), einer Versuchsgruppe 1 (neue Lehrmethode 1) und einer Versuchsgruppe 2 (neue Lehrmethode 2) und teilt die Schüler außerdem in zwei Geschlechtergruppen ein: männlich und weiblich. Mit Hilfe einer zweiseitigen ANOVA kann festgestellt werden, ob es eine Wechselwirkung zwischen der Lehrmethode und dem Geschlecht der Schüler auf die Schülerleistungen gibt.
Wie bei der einseitigen ANOVA werden auch bei der zweiseitigen ANOVA Annahmen über die Daten getroffen, die der einfaktoriellen ANOVA entsprechen und hier daher nicht mehr vertieft werden.
Beispiel
Wir betrachten eine Studie, bei der es um Möglichkeiten geht, den Blutdruck zu senken. Die Variable biofeedback mit den Faktorstufen present/absent besagt, ob die Probanden eine smart watch tragen, die den Blutdruck anzeigt. Die Variable drug mit den Faktorstufen present/absent besagt, ob die Probanden ein blutdrucksenkendes Mittel bekommen haben. 20 Teilnehmer werden zufällig in eine der 4 Gruppen eingeteilt. Die abhängige Variable ist der Blutdruck.
Daten einlesen
Da die beiden abhängigen Variablen meist als “chr” Variablen erkannt werden, müssen diese noch als Faktoren umgewandelt werden.
bpdata<-read.csv2(file="bpdata.csv")
bpdata$biofeedback <-as.factor(bpdata$biofeedback)
bpdata$drug <-as.factor(bpdata$drug)Voraussetzungen
Wir testen zunächst die Voraussetzungen für eine ANOVA. Die abhängige Variable, hier Blutdruck, ist metrisch skaliert. Die Varianzhomogenität testen wir wieder mit dem Levene-Test.
library(car)
leveneTest(bloodpressure ~ biofeedback*drug, data=bpdata)
## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 3 0 1
## 16ANOVA durchführen
Jetzt rechnen wir die ANOVA. Die zweifaktorielle ANOVA funktioniert auch mit der aov() Funktion. Die zweite unabhängige Variable wird nach der Logik “AV~UV1*UV2” aufgenommen. Das Ergebnis der ANOVA können wir wieder mit der summary() Funktion anfordern.
ANOVA2 <- aov(bloodpressure ~ biofeedback*drug, data=bpdata)
summary(ANOVA2)
## Df Sum Sq Mean Sq F value Pr(>F)
## biofeedback 1 500 500.0 8.00 0.01211 *
## drug 1 720 720.0 11.52 0.00371 **
## biofeedback:drug 1 320 320.0 5.12 0.03792 *
## Residuals 16 1000 62.5
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Wir sehen in den Ergebnissen, dass alle 3 Effekte (2 Haupteffekte und Interaktionseffekt) signifikant werden. Das bedeutet, dass “biofeedback” einen signifikanten Einfluss auf den Blutdruck (1. Haupteffekt) hat. Das Medikament “drug” hat einen signifikanten Einfluss auf den Blutdruck (2. Haupteffekt). Bei der Interpretation der Haupteffekte ist jedoch immer Vorsicht geboten, wenn auch der Interaktionseffekt signifikant wird. Hier im Beispiel wird auch der Interaktionseffekt signifikant (3. Zeile “biofeedback:drug”). Das bedeutet, dass sich beide Faktoren auch untereinander signifikant beeinflussen. In diesem Fall ist es immer ratsam über Post-Hoc-Analysen genauer in die Ergebnisse zu schauen. Zudem hängt die Interpretation der Haupteffekte auch vom Typ der Quadratsummen ab (bei unbalancierten Designs).
Interpretation Quadratsummen
R berechnet mit der aov Funktion standardmäßig Typ I Quadratsummen (Sum Sq). Grundsätzlich gibt es bei gleichgroßen Gruppengrößen (wie in diesem Fall) keinen Unterschied zwischen der Verwendung von Typ I, II und III Quadratsummen. Bei ungleichen Gruppengrößen (unbalancierte Designs) hängt die Entscheidung, welchen Quadratsummen-Typ Sie verwenden davon ab, welche Hypothese Sie in Ihrem Forschungsdesign interessiert. Kurz gesagt: Ist vorwiegend der Interaktionseffekt von Interesse sollten Sie Typ III Quadratsummen verwenden. Interessieren Sie eher die Haupteffekte, können Typ I Quadratsummen sinnvoller sein.
Um Typ III Quadratsummen zu erhalten bietet es sich daher an, mit dem afex Paket zu arbeiten.
ANOVA mit afex
Um die zweifaktorielle ANOVA mit dem afex Paket brauchen wir wieder zunächst eine ID Variable (Zwingende Voraussetzung im afex Paket). Diese erzeugen wir nun.
bpdata$ID <- c(1:20).
Dann können wir die ANOVA berechnen. Die Notation entspricht dabei der einfaktoriellen ANOVA afex Paket, nur dass wieder nach der Logik “AV~UV1*UV2” die zweite unabhängige Variable aufgenommen wird.
ANOVA2A <- aov_car(bloodpressure ~ biofeedback*drug+Error(ID), data=bpdata)
## Contrasts set to contr.sum for the following variables: biofeedback, drug
summary(ANOVA2)
## Df Sum Sq Mean Sq F value Pr(>F)
## biofeedback 1 500 500.0 8.00 0.01211 *
## drug 1 720 720.0 11.52 0.00371 **
## biofeedback:drug 1 320 320.0 5.12 0.03792 *
## Residuals 16 1000 62.5
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Wie Sie sehen ergibt sich hier kein Unterschied der Quadratsummen, da ein balanciertes Design vorliegt (Alle Gruppen sind gleich groß).
Um nun die Effekte besser zu verstehen ist es notwendig, Post-Hoc-Analysen durchzuführen.
Post-Hoc-Analyse
Um paarweise t-Tests mit Bonferroni-Korrektur durchzuführen, müssten Sie die Daten zunächst in das Long-Format umwandeln. Hier ist der Tukey HSD-Test die einfachere Wahl, da dieser auch mit Daten im Wide-Format funktioniert.
TukeyHSD(ANOVA2)
## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = bloodpressure ~ biofeedback * drug, data = bpdata)
##
## $biofeedback
## diff lwr upr p adj
## present-absent -10 -17.495 -2.505003 0.0121093
##
## $drug
## diff lwr upr p adj
## present-absent -12 -19.495 -4.505003 0.0037059
##
## $`biofeedback:drug`
## diff lwr upr p adj
## present:absent-absent:absent -2 -16.3051 12.305099 0.9775889
## absent:present-absent:absent -4 -18.3051 10.305099 0.8534038
## present:present-absent:absent -22 -36.3051 -7.694901 0.0022719
## absent:present-present:absent -2 -16.3051 12.305099 0.9775889
## present:present-present:absent -20 -34.3051 -5.694901 0.0051230
## present:present-absent:present -18 -32.3051 -3.694901 0.0115535Wie Sie sehen sind die Paarvergleiche hier recht unübersichtlich, jedoch lassen sich schnell erste Tendenzen erkennen. Bei allen drei signifikanten Paarvergleichen steht “present:present”. Dies bedeutet, dass sich diese Gruppe mit smartwatch (biofeedback) und Medikament (drug) signifikant von allen anderen drei Gruppen unterscheidet. Um dies noch klarer zu sehen, hilft uns ein sogenannter Interaktionsplot.
Interaktionsplot
Ein Interaktionsdiagramm ist eine grafische Darstellung der Beziehung zwischen zwei oder mehr Variablen in einem Datensatz, bei der die Auswirkung einer Variablen auf die andere durch die Steigung der gezeichneten Linien dargestellt wird. Interaktionsdiagramme werden verwendet, um Wechselwirkungen zwischen Vorhersagevariablen zu identifizieren und zu visualisieren.
- Parallele Linien in einem Interaktionsdiagramm deuten darauf hin, dass es keine Interaktion zwischen den aufgezeichneten Variablen gibt. Das bedeutet, dass die Auswirkung der einen Variablen auf die andere Variable über die Niveaus der anderen Variablen hinweg konstant ist.
- Sich kreuzende Linien in einem Interaktionsdiagramm deuten darauf hin, dass es eine Interaktion zwischen den dargestellten Variablen gibt. Dies bedeutet, dass die Wirkung einer Variablen auf die andere Variable über die Niveaus der anderen Variablen hinweg nicht konstant ist und dass die Beziehung zwischen den Variablen nicht linear ist.
- Die Steigung der Linien in einem Interaktionsdiagramm kann ebenfalls wichtige Informationen über die Beziehung zwischen den Variablen liefern. Eine steilere Neigung deutet auf eine stärkere Beziehung zwischen den Variablen hin, während eine flachere Neigung auf eine schwächere Beziehung hindeutet.
Es ist wichtig zu beachten, dass die Interpretation der Linien in einem Interaktionsdiagramm unter Berücksichtigung des Kontexts der Daten und der Forschungsfrage vorgenommen werden sollte. Die Linien können je nach der spezifischen Situation und den aufgezeichneten Variablen unterschiedlich interpretiert werden.
Wir generieren einen Interaktionsplot, dem Paket phia und der Funktion interactionMeans(). Dabei nutzen wir die plot() Funktion.
plot(interactionMeans(ANOVA2))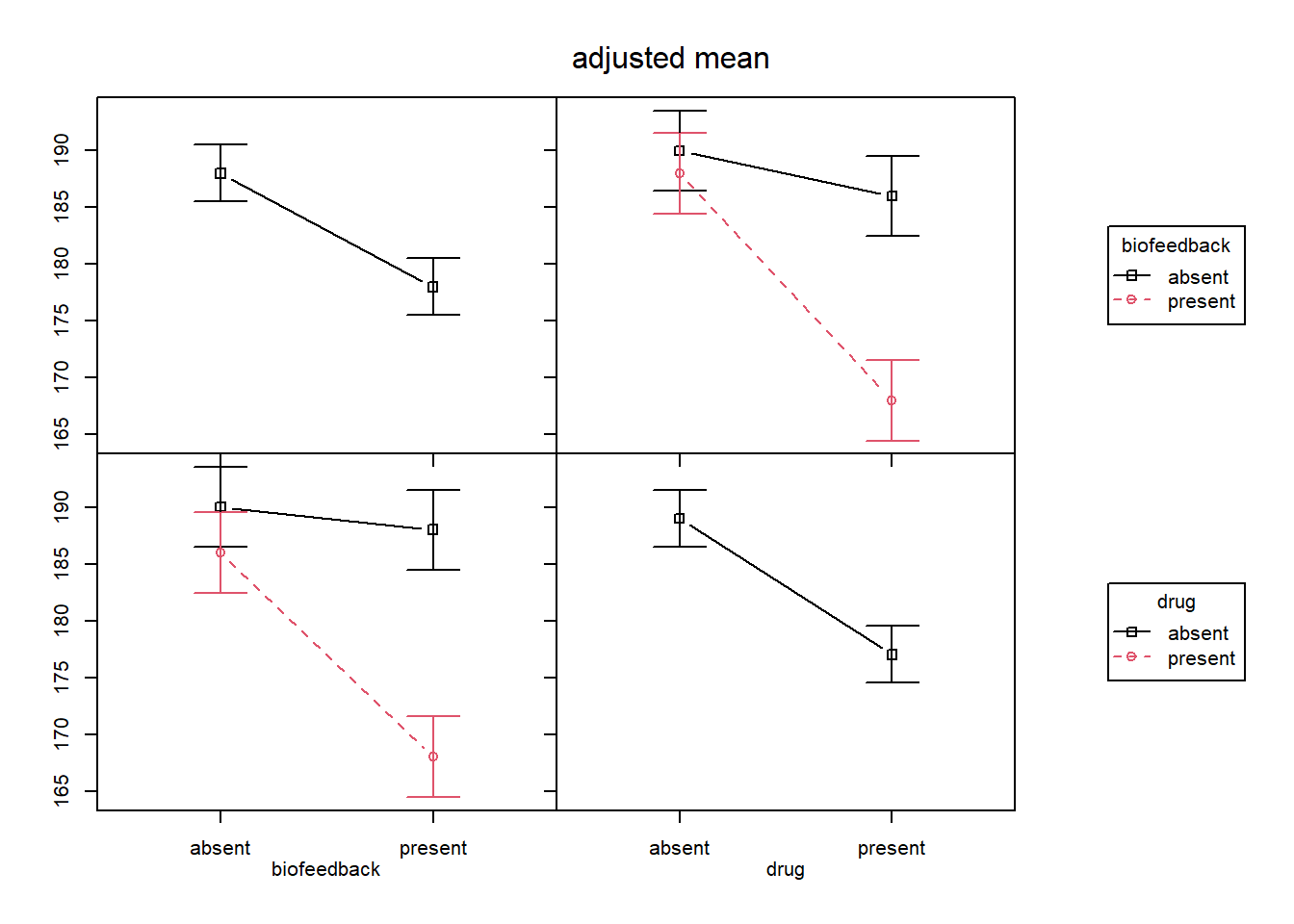
Alternativ der Interaktionsplot aus dem afex Paket:
afex_plot(ANOVA2A,dv="bloodpressure",x="biofeedback", trace="drug")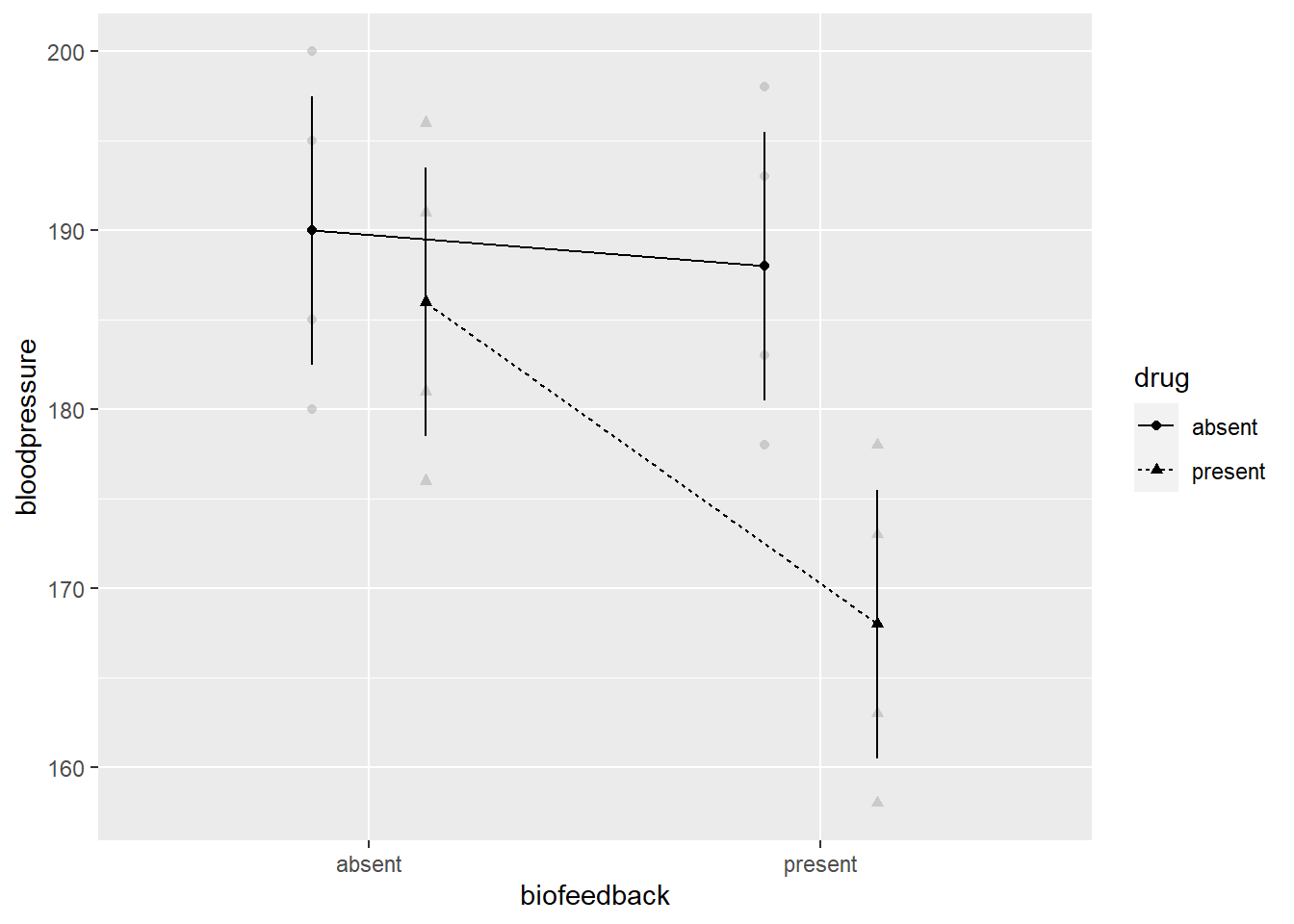
Wie in den Interaktionsplots recht einfach zu sehen ist unterscheidet sich die Gruppe, die beides verwendet hat (“biofeedback” und “drug”), signifikant von den übrigen drei Gruppen (die sich jeweils nicht unterscheiden). Das bedeutet, dass nur Patienten, die beides verwenden, eine sig. Absenkung des Blutdrucks erfahren. Die beiden Haupteffekte sind daher hinfällig: Alleine haben sowohl die Smartwatch (“biofeedback”) als auch das Medikament (“drug”) keine sig. Wirkung. Die reine Interpretation der Haupteffekte hätte uns also hier zu einem falschen Ergebnis geführt. Dies resultiert aus der Tatsache, dass die Haupteffekte nicht den einzelnen Effekt eines Faktors berücksichtigen, sondern den Mittelwert des Effekts mit und ohne den anderen Faktor. Der Haupteffekt zur Smartwatch (“biofeedback”), berücksichtigt also sowohl die Situation mit und ohne Medikament (drug) und umgekehrt. Wird der Interaktionseffekt signifikant, lohnt es sich also immer genauer hinzusehen und Post-Hoc-Analysen durchzuführen.
In diesem Video zeige ich, wie das in R funktioniert:
Übungsaufgabe
Wir wollen die Wirksamkeit der drei Diäten vergleichen und nutzen den Datensatz diet3.csv. Wir nutzen nun noch das Geschlecht (0=Weiblich, 1=Männlich) der Versuchspersonen. Ziel dieser Analyse ist es herauszufinden, ob bestimmte Diäten für Männer bzw. Frauen besonders geeignet sind.
Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.


