Deskriptive Statistik
2 Kennwerte
2.0 Einführung Kennwerte
Das Ziel der deskriptiven Statistik ist es, Muster in den Daten sichtbar zu machen. Das bedeutet, konkret Daten in eine übersichtliche Form zu bringen, die für den Betrachter leicht fassbar ist. Dazu beschäftigt sich die deskriptive Statistik mit der Organisation, Darstellung und Zusammenfassung von Daten. Dies kann grundsätzlich auf zwei unterschiedliche Weisen erfolgen:
- Daten können anhand von Kennwerten zusammengefasst werden
- Daten können graphisch (oder tabellarisch) dargestellt werden (siehe Kapitel 3).
Beiden Ansätzen gemein ist das Ziel, große Mengen an Daten und komplexe Zusammenhänge schnell und einfach verständlich zu machen. Leider erkennt man bei umfangreichen Daten auf den ersten Blick oft nicht, was in den Daten steckt und es ist schwierig, die Daten, also viele Werte auf einer Variablen, mit Worten zu beschreiben. Stellen Sie sich vor, Sie werden von einem Freund gefragt wie alt die Studierenden in Ihrem Studiengang sind. Selbst wenn Sie eine Liste (Daten) mit dem jeweiligen Alter (Merkmalsausprägung) aller Kommilitonen (Merkmalsträger) vor sich liegen haben, ist es nicht einfach eine kurze und präzise Antwort auf diese Frage zu geben. Sie könnten z.B. eine Tabelle erstellen, die die Häufigkeiten der Altersgruppen wiedergibt (z.B. 12 Studenten sind 18 Jahre, 15 Studenten sind 19 Jahre etc.). Kennwerte erlauben Ihnen hier eine einfachere und schnellere Antwort. So könnten Sie zum Beispiel sagen der jüngste Student ist 17 und der Älteste 36 (Spannweite), oder das Durchschnittsalter (Mittelwert) ist 22,5 Jahre. Kennwerte haben dabei den Anspruch die Verteilung einer Variablen in meist nur einem einzigen Wert (z.B. Durchschnittsalter) wiederzugeben. Dabei geht natürlich auch Informationsgehalt verloren. Daher werden wir uns im Folgenden damit Beschäftigen, welche Kennwerte für welche Fragestellungen geeignet sind und wie man diese berechnet.
Video 2.0 Kennwerte – Einführung
Statistische Kennwerte (auch Maßzahlen oder kurz Statistiken genannt) haben die Funktion, in zusammengefasster (aggregierter) Form Auskunft über Eigenschaften von Verteilungen zu geben. Aus vielen einzelnen Werten werden also einige wenige resultierende Werte gebildet, die Aussage über die Beschaffenheit einer Verteilung geben. Statistische Kennwerte sind oft die Grundlage für weitere statistische Auswertungen.
Mithilfe von statistischen Kennwerten können wir die Verteilung einer Variablen hinsichtlich der zentralen Tendenz bzw. der Streuung ihrer Messwerte beschreiben.
- Maße der zentralen Tendenz (auch Lokationsmaße oder Lagemaße) repräsentieren alle Messwerte einer Verteilung zusammenfassend und zeigen sozusagen den Schwerpunkt der Verteilung auf.
- Streuungsmaße (auch Variabilitäts- oder Dispersionsmaße) geben Auskunft über die Variation der Messwerte, also darüber, wie unterschiedlich ein Merkmal verteilt ist und wie weit diese um den Schwerpunkt streuen.
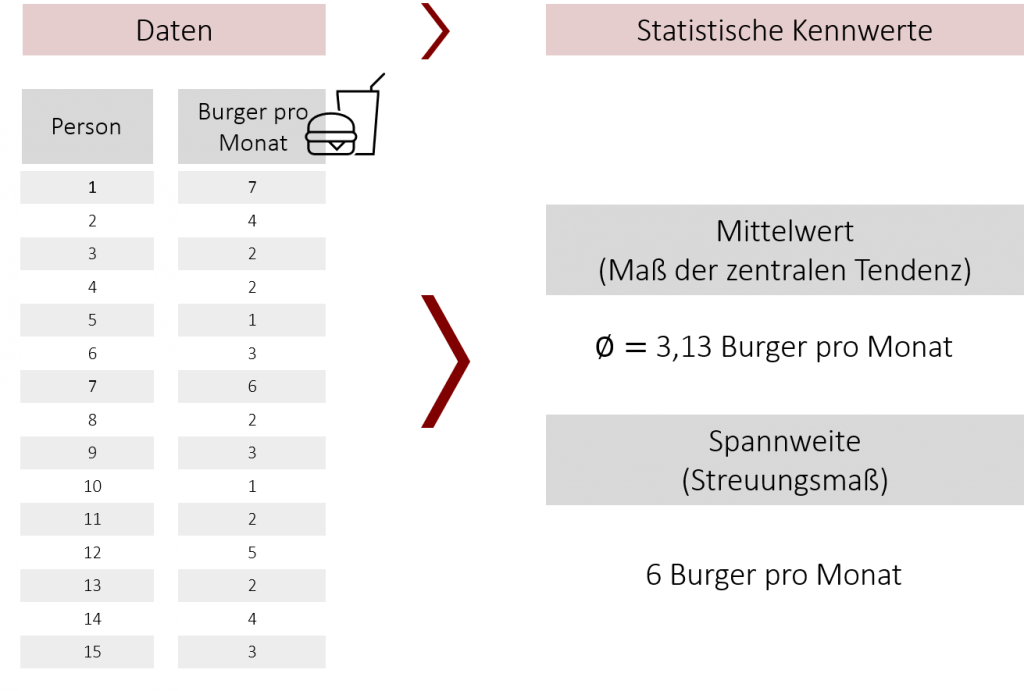
Wir werden uns nun zunächst den Maßen der zentralen Tendenz näher widmen.
2.1 Maße der zentralen Tendenz (auch Lokationsmaße oder Lagemaße)
Nehmen wir an, wir wollen jemandem mitteilen, was das Ergebnis einer Umfrage ist, beispielsweise:
- wie sympathisch ist Angela Merkel?
- wie viele Burger essen Kinder in Deutschland?
- sind Kinder in Deutschland übergewichtig?
Hierfür brauchen wir einen Kennwert, der alle Messwerte einer Verteilung zusammenfassend repräsentiert. Hierzu geben Lagemaße Auskunft, indem sie die zentrale Tendenz einer Verteilung in Einheiten der zugrunde liegenden Skala angeben, also beschreiben, wo das Zentrum oder der Schwerpunkt einer Verteilung liegt. Das bedeutet, dass ein Wert möglichst gut die ganze Verteilung repräsentieren soll, was einen ziemlich hohen Anspruch darstellt. Daher ist es unerlässlich, neben diesen Kennwerten auch immer zusätzlich die ganze Verteilung zu betrachten und die Lagemaße gegebenenfalls um Streuungsmaße zu ergänzen.
Gebräuchlich sind drei verschiedene Maße der zentralen Tendenz bzw. Lagemaße:
- Modus
- Median
- Arithmetisches Mittel (Mittelwert)
Darüber hinaus gibt es weitere Maße der zentralen Tendenz für spezielle Anwendungen wie das geometrische Mittel oder das getrimmte Mittel. Wir wollen uns im Folgenden aber nur mit den Erstgenannten beschäftigen und werden diese nun vertiefen.
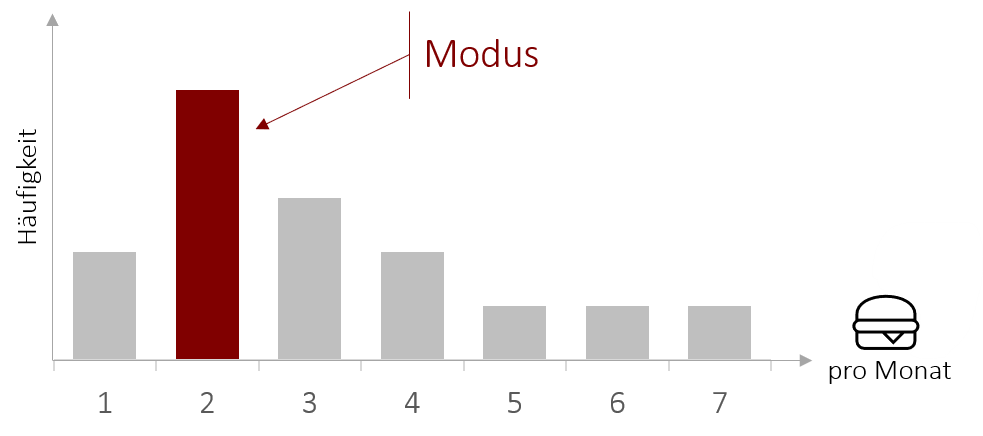
2.2 Modus
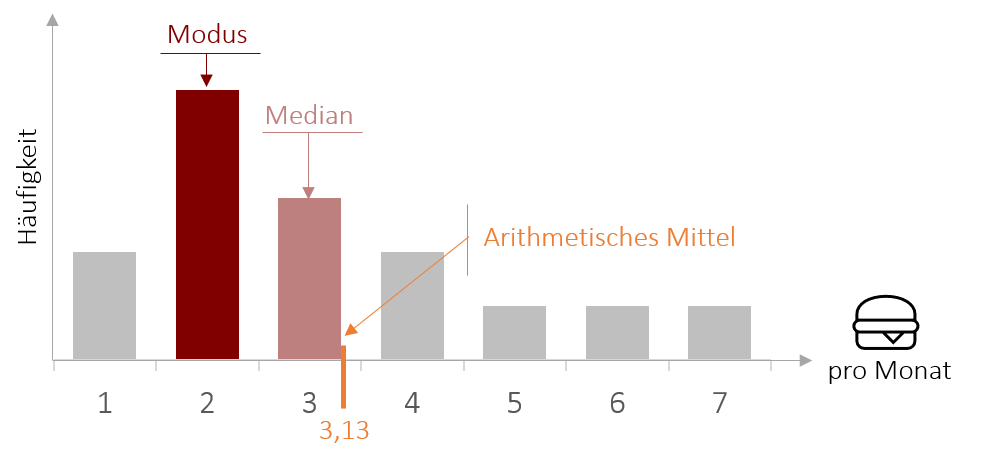
Der Modus (Modalwert) ist der Wert, der in der Verteilung einer diskreten Variable am häufigsten vorkommt (Wenn Sie nicht mehr ganz sicher sind, was eine diskrete Variable ist, schauen Sie doch nochmal in Kapitel 1.3). Folglich ist es auch der Wert, der am wahrscheinlichsten ist, wenn wir zufällig eine Stichprobe aus der Gesamtheit der Messwerte herausgreifen. Es kann auch mehr als einen Modus geben (Plural: Modi). Man spricht dann von einer bimodalen bzw. multimodalen Verteilung.
Kennwerte werden mit lateinischen Buchstaben – üblicherweise kursiv – angegeben. Die Abkürzung für den Modus ist dabei Mo.
Rechenbeispiel
Nehmen Sie an, wir erheben bei 10 Studierenden die Körpergröße und erhalten folgende Werte:
159 cm, 178 cm, 152 cm, 193 cm, 155 cm, 166 cm, 170 cm, 182 cm, 178 cm, 179 cm
Was ist hier der Modus?
Der Modus ist Mo = 178 cm. Denn der Messwert 178 cm kommt zweimal, alle anderen Werte kommen jeweils nur einmal vor.
Achtung: Der Modus ist der Wert mit der höchsten Auftrittshäufigkeit, nicht der höchste Wert!
2.3 Median
Der Median (Medianwert) ist der Wert, der eine der Größe nach geordnete Häufigkeitsverteilung, in zwei gleichgroße Hälften teilt. Hierfür muss man bei der Berechnung also zwei Schritte berücksichtigen. Zunächst ordnet man alle Werte der Größe nach an (z.B. von dem geringsten bis zum höchsten Burgerkonsum) und dann sucht man den Wert, der genau in der Mitte liegt. Anders ausgedrückt ist das am Beispiel des Burgerkonsums genau die Person, bei der es gleich viele Personen gibt, die weniger und die jeweils mehr Burger als sie selbst essen. Hierbei ist jedoch zu beachten, dass es nicht immer die eine Person gibt, die genau in der Mitte steht.
- Bei ungerader Anzahl von Werten ist es der Wert in der Mitte, wenn man die Messwerte der Größe nach anordnet.
- Bei gerader Anzahl von Werten wird das arithmetische Mittel aus dem größten Wert der unteren Hälfte und dem kleinsten Wert der oberen Hälfte berechnet.
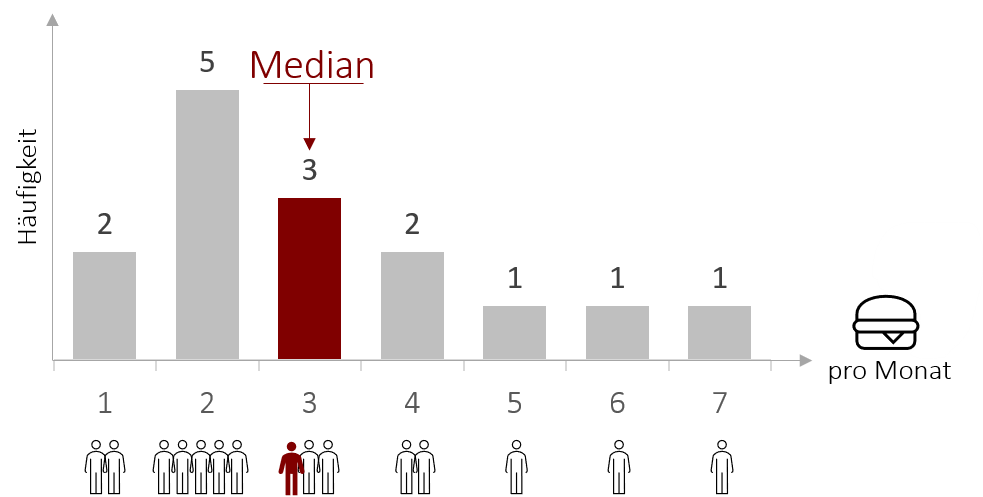
Für eine sehr große Anzahl an Werten (oder Personen) kann es oft sehr aufwendig sein, die Mitte zu bestimmen. Hierfür kann man sich mit der folgenden Formel behelfen:
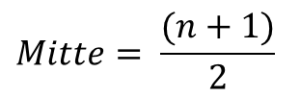
In dieser Formel steht das „n“ für die Anzahl der Werte oder Personen. Gibt es beispielsweise 213 Personen, so ist die Mitte bei 213+1 also 214 : 2 = 107. Das heißt Sie suchen in der (nach Größe geordneten) Liste der Personen die 107. Person heraus.
Statistische Eigenschaften des Median:
- Setzt mindestens Ordinalskalenniveau voraus.
- Die Summe der absoluten Abweichungen vom Median ist minimal.
Das heißt, der Median ist der Wert, von dem alle übrigen Werte im Durchschnitt am wenigsten abweichen. - Vorteil: Der Median ist relativ wenig anfällig gegenüber Ausreißern.
Die Abkürzung für den Median ist Md.
Rechenbeispiel Median 1
Nehmen Sie an, wir erheben bei 11 Studierenden die Anzahl der Follower auf Instagram und erhalten folgende Werte:
108, 103, 1252, 121, 93, 57, 40, 53, 22, 116, 98
Was ist hier der Median?
Berechnung:
- Wir bringen die Zahlen in eine Reihenfolge: 22,40,53,57,93,98,103,108,116,121,1252
- Wir bestimmen, welcher Wert in der Mitte liegt. Optisch oder über die Formel (11 + 1 / 2) = 6
- Der 6. Wert ist 98 also lautet unser Median: Md=98
Rechenbeispiel Median 2
Was wäre nun wenn wir den Wert 1252 herausnehmen, da sich herausstellt, dass dies eine Fehleingabe war? Somit haben wir nun noch 10 Studierende und die jeweilige Anzahl der Follower:
108, 103, 121, 93, 57, 40, 53, 22, 116, 98
Was ist dann der Median?
Die Berechnung erfolgt genauso wie bisher auch.
- Wir bringen die Zahlen in eine Reihenfolge: 22,40,53,57,93,98,103,108,116,121
- Wir bestimmen, welcher Wert in der Mitte liegt. Da wir nun nur noch 10 Werte und damit eine gerade Anzahl an Werten haben, müssen wir das arithmetische Mittel aus dem größten Wert der unteren Hälfte und dem kleinsten Wert der oberen Hälfte berechnen. Der Median liegt zwischen dem 5. und 6. Wert, also zwischen „93“ und „98“.
- Md = ((93+98))/2 = 95,5
Diese beiden Rechenbeispiele sollen auch zeigen, dass sich durch die Herausnahme eines hohen Wertes der Median verändert und erwartungsgemäß sinkt (von 98 im oberen Beispiel auf 95,5 im unteren). Behalten Sie dieses Ergebnis im Hinterkopf, da wir im nächsten Kapitel das arithmetischen Mittel für die selben Zahlen berechnen werden.
Video 2.2 Kennwerte Lagemaße Median und Modus
2.4 Arithmetisches Mittel (Mittelwert)
Der Mittelwert bzw. das arithmetische Mittel ist die Summe aller Messwerte dividiert durch die Anzahl der Messwerte n. Auch wenn der Mittelwert vielen aus dem Alltag bekannt ist, so scheint die Formel für diesen Kennwert auf den ersten Blick doch komplex:
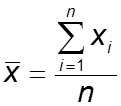
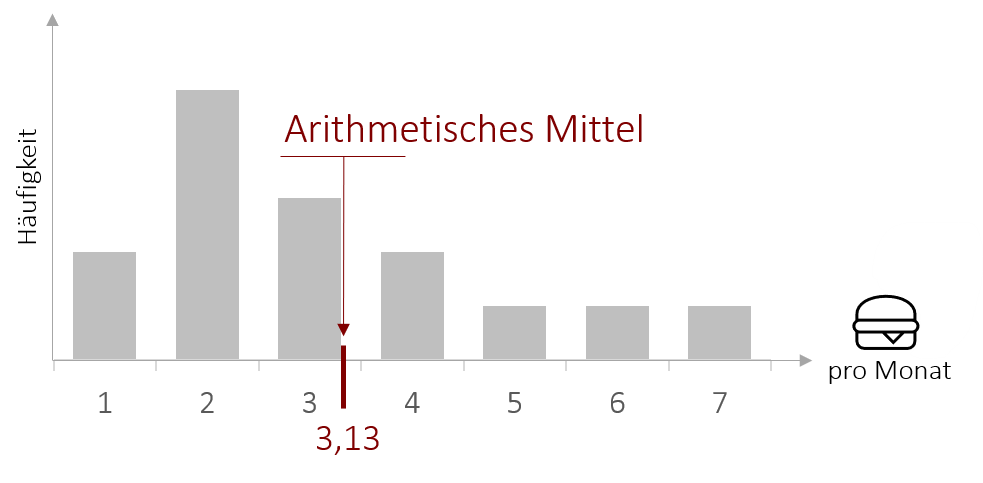
Das mathematische Summenzeichen ∑ sagt aus, dass alle Werte eine Variablen x vom ersten Wert (i=1) bis zum n-ten Wert aufsummiert werden. Beispielsweise könnten wir das Alter unserer Mitarbeiter abfragen und unsere Variable x (in diesem Fall das Alter) hat die drei Werte: x1 = 32, x2 =19 und x3 = 27. Dann bedeutet das Summenzeichen ∑, dass wir alle Werte x vom Wert mit dem Index 1 bis zum letzten, in diesem Fall 3, aufsummieren. Also in diesem Fall einfach 32 + 19 + 27 = 78. Im Folgenden wird dann durch die Anzahl der Werte (n) geteilt. also in diesem Fall 78 /3 = 26. Anders als beim Median fließen beim arithmetischen Mittel alle Werte in die Berechnung des Mittelwerts mit ein, dadurch bekommen auch Ausreißer und Extremwerte Gewicht, was dazu führen kann, dass der Mittelwert die wahre zentrale Tendenz der Werte nur verzerrt wiedergibt. Im Falle unseres Burgerkonsums-Beispiels erhalten wir einen Mittelwert von 3,13 Burgern pro Monat.
Die Abkürzung für das arithmetische Mittel ist ![]() (üblicherweise gesprochen als x – quer).
(üblicherweise gesprochen als x – quer).
Statistische Eigenschaften:
- Setzt mindestens Intervallskalenniveau voraus.
- Die Summe der Abweichungen aller Messwerte vom Mittelwert ist Null.
- Die Summe der quadrierten Abweichungen der Messwerte vom Mittelwert ist ein Minimum.
- Es werden alle Werte bei der Berechnung berücksichtigt, dadurch ist der Mittelwert anfällig für Ausreißer.
Rechenbeispiel 1
Wie ist der Mittelwert der Anzahl der Instagram-Follower der 11 Studierenden aus dem obigen Beispiel?
Wir haben die Werte: 108, 103, 1252, 121, 93, 57, 40, 53, 22, 116, 98
Wir setzen in die Formel von oben ein:
![]()
Rechenbeispiel 2
Was wäre, wenn wir den Extremwert wieder streichen?
108, 103, 1252, 121, 93, 57, 40, 53, 22, 116, 98
![]()
Wenn Sie die beiden Rechenbeispiele betrachten, sollte Ihnen auffallen, dass der Mittelwert sich durch die Herausnahme eines einzelnen Wertes sehr stark ändert (von 187,5 auf 81,1). Im gleichen Fall (bei den gleichen Werten) hat sich der Median jedoch nur von 98 auf 95,5 verringert. Dies zeigt eindrucksvoll wie anfällig das arithmetische Mittel für Ausreißer ist: Bereits ein einzelner Wert kann den Mittelwert sehr stark beeinflussen.
Video 2.1 Kennwerte – Arithmetisches Mittel
2.5 Maße der zentralen Tendenz – Übersicht
Ihr Leben ist wahrscheinlich nun etwas komplizierter geworden. Während Sie bisher einfach den Mittelwert berechnet haben, müssen Sie sich zukünftig zwischen mindestens drei Kennwerten entscheiden, die alle den Anspruch haben, die zentrale Tendenz einer Variablen aufzuzeigen. Welches Lagemaß ist nun das Beste? Das hängt natürlich ganz davon ab, was für eine Verteilung und was für eine Variable Sie vorliegen haben. Ist die interessierte Variable nominalskaliert, so bleibt nur der Modus. Haben Sie eine ordinalskalierte Variable vorliegen, so könnten Modus oder Median zum Einsatz kommen und ab Intervallskalenniveau können alle drei Kennwerte verwendet werden. In diesem Fall gilt es abzuwägen wie stark die Verzerrung durch Ausreißer auf den Mittelwert zu erwarten ist. Bei sehr gleichmäßigen Verteilungen ist der Mittelwert die beste Wahl, bei ungleichmäßigen Verteilungen mit Ausreißern ist der Median oft die sensiblere Entscheidung. Die folgende Tabelle gibt nochmal eine Übersicht hierzu:
| Skalenniveau der Variable |
Modus | Median | Mittelwert |
| Nominal | ja | nein | nein |
| Ordinal | ja | ja | nein |
| Intervall | ja | ja | ja |
Video 2.3 Kennwerte – welches Lagemaß ist das Richtige?
2.6 Streuungsmaße
Verteilungen können gleiche Maße der zentralen Tendenz (z.B. Mittelwert) besitzen, dabei aber unterschiedlich breit streuen (d.h. unterschiedlich stark vom Mittel abweichen). Nehmen wir als Beispiel an, ein Schüler wird von seinen Eltern gefragt, wie denn die anderen Schüler in der Mathe-Klausur abgeschnitten haben. Wahrheitsgemäß antwortet er, dass der Mittelwert in der Klasse bei einer Note 3 lag. Das kann jedoch ganz unterschiedliche Gründe haben: Alle vier Verteilungen, die nachfolgend abgebildet sind, haben den gleichen Mittelwert von 3. Sie sehen jedoch sofort, dass die Verteilungen sehr unterschiedlich sind. Im einen Extremfall haben alle Schüler eine 3 geschrieben, im anderen Extremfall hat kein einziger Schüler eine 3 geschrieben.

Aus diesem Grund ist es wichtig, auch für die Streuung ein Maß zu finden, das mit nur einem Wert einen Rückschluss auf die Streuung zulässt. Die nächste Gruppe der Kennwerte, die sogenannten Streuungsmaße, haben genau diese Aufgabe.
Streuungsmaße geben grundsätzlich Auskunft über die Variabilität der Werte, d.h. wie weit die Werte um die zentrale Tendenz verteilt liegen. Wir unterscheiden folgende Streuungsmaße (manchmal auch Dispersionsmaße genannt):
- Spannweite/Range
- Varianz
- Standardabweichung
- Interquartilsabstand
Im Folgenden wollen wir uns nun genauer mit diesen Kennwerten auseinandersetzen.
2.7 Spannweite / Range
Die Spannweite (auch: Variationsbreite; bzw. aus dem englischen Range) ist die Differenz zwischen dem größten (Maximum) und dem kleinsten Wert (Minimum).
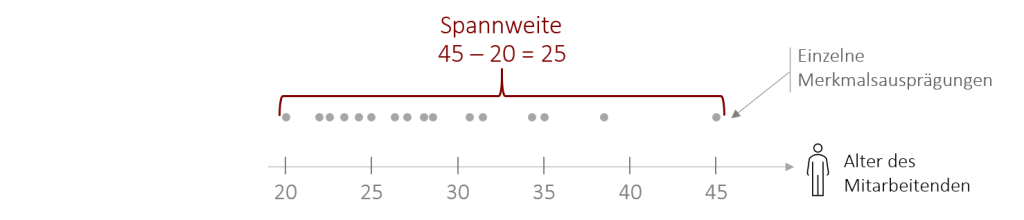
Beispiele
Im Instagram-Follower-Beispiel:
22, 40, 53, 57, 93, 1.252, 98, 103, 108, 116, 121
Was ist hier die Spannweite?
Berechnung:
- Minimum und Maximum bestimmen: Minimum = 22, Maximum = 1.252
- Spannweite = 1.252– 22 = 1.230
Der Nachteil der Spannweite ist, dass nicht alle Werte berücksichtigt werden (nur die Randwerte finden Berücksichtigung) und die Spannweite damit sehr stark von Extremwerten abhängig ist.
Video 2.4 Kennwerte Streuungsmaße Spannweite
2.8 Interquartilsabstand
Eine Lösung für das letztere Problem ist es, die Extremwerte aus der Analyse auszuschließen und sich z.B. nur mit den 50% der Werte in der Mitte der Verteilung zu beschäftigen. Dies ist der sogenannte Interquartilsbereich, oder Interquartilsabstand. Im Gegensatz zur Spannweite, die das Minimum und Maximum des gesamten Datensatzes abbildet, repräsentiert der Interquartilsabstand die mittleren 50% der Werte und ist damit nur wenig durch Ausreißer (besonders große oder besonders kleine Werte) beeinflusst. Die Berechnung ähnelt dem Median. Zunächst ordnet man die Werte der Größe nach an.
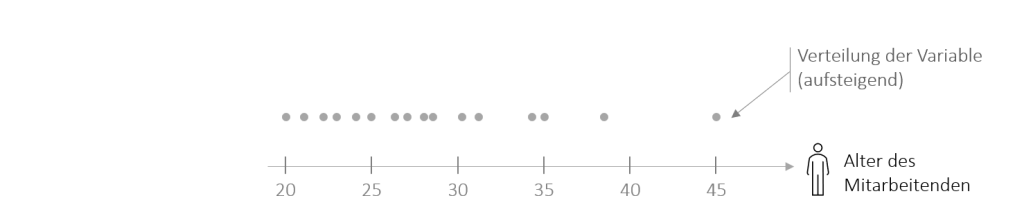
Im zweiten Schritt teilt man die Verteilung in vier gleiche Teile auf. Die vier daraus resultierende Quartile finden in der Statistik häufig Verwendung und werden 1., 2., 3. und 4.Quartil genannt.
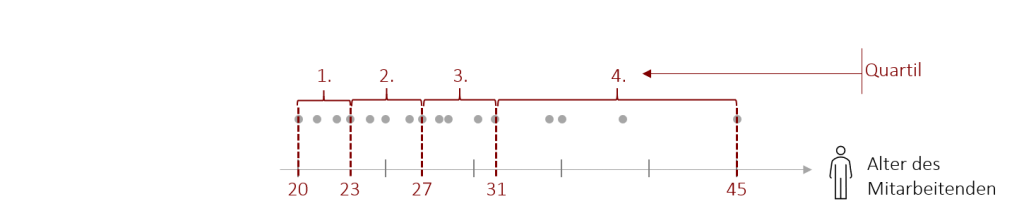
Die Spannweite zwischen Beginn des zweiten und Ende des dritten Quartils repräsentiert dabei den Interquartilsabstand.
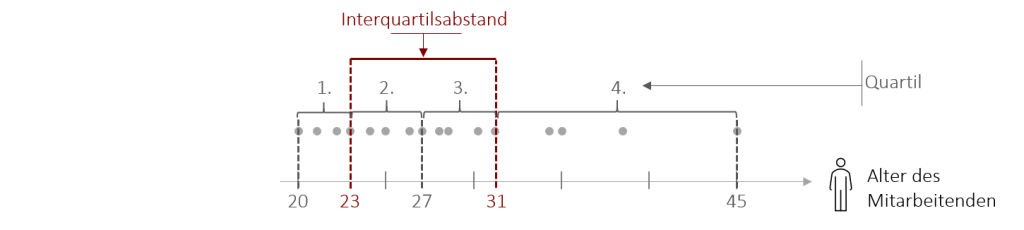
Diese zwei Randwerte lassen sich mit der Formel 0,25 ⋅ n bzw. 0,75 ⋅ n sehr leicht ermitteln. In unserem Beispiel ergibt dies bei n = 16 Werten den 4. Wert (0,25 ⋅ 16 =4) und den 12.Wert (0,75 ⋅ 16 = 12). Erhält man bei dieser Berechnung einen ungeraden Wert, dann wird stets aufgerundet. Haben wir zum Beispiel n = 10 Werte, so nimmt man den 3. Wert (0,25 ⋅ 10 = 2,5 – aufgerundet 3) und den 8. Wert (0,75 ⋅ 10 = 7,5 aufgerundet 8).
Die Abkürzung für den Interquartilsabstand ist IQR (aus dem Englischen für interquartil range).
Statistische Eigenschaften:
- Es liegen immer insgesamt 50% der Daten innerhalb des Interquartilsabstands
- Vorteil: Der Interquartilsabstand ist nicht anfällig gegenüber Ausreißern
Beispiele
Im Instagram-Follower-Beispiel:
22, 40, 53, 57, 93, 1.252, 98, 103, 108, 116, 121, 125
Was ist hier der Interquartilsabstand ?
Berechnung:
- Wir bringen die Zahlen in eine Reihenfolge: 22,40,53,57,93,98,103,108,116,121,125, 1252
- Wir bestimmen die Position der beiden Randwerte:
0,25 x 12 = 3 (also den 3.Wert – 53)
0,75 x 12 = 9 (also den 9.Wert – 116) - Wir bilden die Differenz: 116-53 = 63. Das heißt der Interquartilsabstand ist 63.
Letztlich berücksichtigt der Interquartilsabstand auch nur zwei „Randwerte“ und nicht alle Werte der Verteilung. Daher wollen wir uns nun damit beschäftigen, wie die Streuung einer Variablen unter Berücksichtigung aller Werte ermittelt werden kann.
Video 2.7 Kennwerte Streuungsmaße Interquartilsabstand
2.9 Varianz
Analog zum arithmetischen Mittel ist die Varianz ein Kennwert, der alle Werte einer Verteilung miteinbezieht. Das Vorgehen ist dabei zunächst denkbar einfach. Die Varianz basiert auf dem arithmetischen Mittel und berücksichtigt alle Abweichungen vom Mittelwert. Die Abstände aller Werte zum Mittelwert werden einfach aufsummiert. Je weiter die Werte um den Mittelwert herum streuen, desto größer sollte dieser Kennwert werden. Das Problem dabei: Positive und negative Abweichungen heben sich hierbei stets exakt zu 0 auf (was an der Definition des Mittelwerts liegt). Die einfache Lösung: Die Abweichungen der Werte zum Mittelwert werden quadriert. Man berechnet also die Summe der quadrierten Abweichung (Quadratsumme, engl. sum of squares).

Die Abkürzung für die hier dargestellte Quadratsumme ist QS.
Doch auch hier entsteht ein neues Problem: Die Größe der Quadratsumme hängt von der Anzahl der Messwerte bzw. Merkmalsträger ab. Das heißt, je mehr Werte vorliegen, desto größer wird automatisch die Varianz werden. Da wir aber ein Maß haben wollen, das unabhängig von der Größe der Stichprobe ist, relativiert man das Ergebnis noch an der Anzahl der Merkmalsträger (n) der Stichprobe. Die Varianz ist also die Summe der quadrierten Abweichungen vom Mittelwert, dividiert durch die Anzahl der Messwerte n. Oder anders ausgedrückt bezeichnet die Varianz also die durchschnittliche (quadrierte) Abweichung vom Mittelwert.

Die Abkürzung für die Varianz s2.
Die Varianz nimmt umso größere Werte an, je stärker die einzelnen Messwerte von ihrem Mittelwert abweichen.
Das Quadrieren der Abweichungen hat folgende mathematische Eigenschaften:
- Alle Abweichungen werden positiv
- Größere Abweichungen werden stärker gewichtet
Der Vorteil der Varianz ist, dass zum einen alle Werte einer Verteilung mitberücksichtigt werden und zum anderen die Größe des Kennwerts ein Maß dafür ist, wie stark die Werte um den Mittelwert streuen. Daher hat die Varianz in der Statistik auch eine hohe Bedeutung. Dieser Kennwert hat jedoch auch einen Nachteil: Der resultierende Wert ist wegen des Quadrierens der Abweichungen auf den ersten Blick nur schwer interpretierbar.
Das Quadrieren hat den unschönen Nebeneffekt, dass die Varianz ein Maß für die mittleren quadrierten Abweichungen ist. Um einen Kennwert, der besser interpretierbar ist, zu erhalten, müssen wir das Quadrieren rückgängig machen. Daher ist die Lösung: Wir ziehen am Ende einfach die Wurzel aus der Varianz. Diesen Kennwert nennt man die Standardabweichung.
2.10 Standardabweichung
Die Standardabweichung ist die positive Wurzel aus der Varianz (hier wird das Quadrieren wieder rückgängig gemacht). Daher ist die Standardabweichung einfach die Wurzel der Varianz und die Formel lautet entsprechend:

Die Abkürzung für die Standardabweichung ist s oder sd (aus dem Englischen für standard deviation)
Wir haben nun ein Maß für die durchschnittlichen Abweichungen vom Mittelwert gefunden, welches in der Maßeinheit einer gegebenen Skala dargestellt wird. Die Standardabweichung ist eine Kenngröße, die angibt, wie gut ein Mittelwert eine Verteilung repräsentiert. Je größer die Standardabweichung im Verhältnis zum Mittelwert, umso mehr weichen die einzelnen Messwerte vom Mittelwert ab. Wenn wir also zum Beispiel wissen, dass Studierende in einem Kurs im Mittel 21 Jahre alt sind und wir nun zusätzlich wissen, dass die Standardabweichung 2 Jahre beträgt , dann hilft uns das nun, die Verteilung besser zu verstehen. In diesem Fall lässt sich ableiten, dass das Alter der Studierenden nur sehr wenig, durchschnittlich eben nur um 2 Jahre, vom Mittelwert abweicht. Die Standardabweichung, die Ursprünglich von Karl Pearson entwickelt wurde[1], ist in der Statistik sehr beliebt, da Sie noch mehr Rückschlüsse zulässt, wenn die zugrundeliegende Variable normalverteilt ist.
Video 2.5 Kennwerte Streuungsmaße Varianz & Standardabweichung
2.11 Die Normalverteilung
Die Normalverteilung wird für den zweiten Teil des Buchs Inferenzstatistik noch sehr relevant werden. Wir wollen Sie aber an dieser Stelle schon einführen, da sie auch in der deskriptiven Statistik durchaus Anwendung findet. Der Begriff der „Normalverteilung“ wurde geprägt von Adolphe Quetelet, der im Jahr 1844 eine verblüffende Entdeckung machte. Bei Untersuchungen des Brustumfangs von mehreren tausend Soldaten stellte er fest, dass die gemessenen Werte immer einer symmetrischen, glockenförmigen Verteilung folgen. Diese Verteilung, die schon 1809 von Carl Friedrich Gauß theoretisch hergeleitet wurde, findet sich nahezu überall in der Natur. Ob man die Größe von Berggorillas misst, oder die Sprungweite von Laubfröschen – in der Natur sind nahezu alle Werte normalverteilt. Die Normalverteilung ist eine unimodale (=eine Spitze), symmetrische (=links und rechts gleich) Verteilung mit glockenförmigem Verlauf. Dabei gibt es jedoch nicht die eine feste Normalverteilung. Jede Normalverteilung ist anders, aber kann durch nur zwei Werte fest definiert werden: Wenn der Mittelwert und die Standardabweichung bekannt sind, dann ist auch die Verteilung der Werte bekannt. Wenn Sie also eine normalverteilte Variable betrachten (z.B. die Größe von Menschen), dann reicht es Ihnen, wenn Sie diese beiden Kennwerte wissen und Sie können die gesamte Verteilung darstellen und beschreiben.
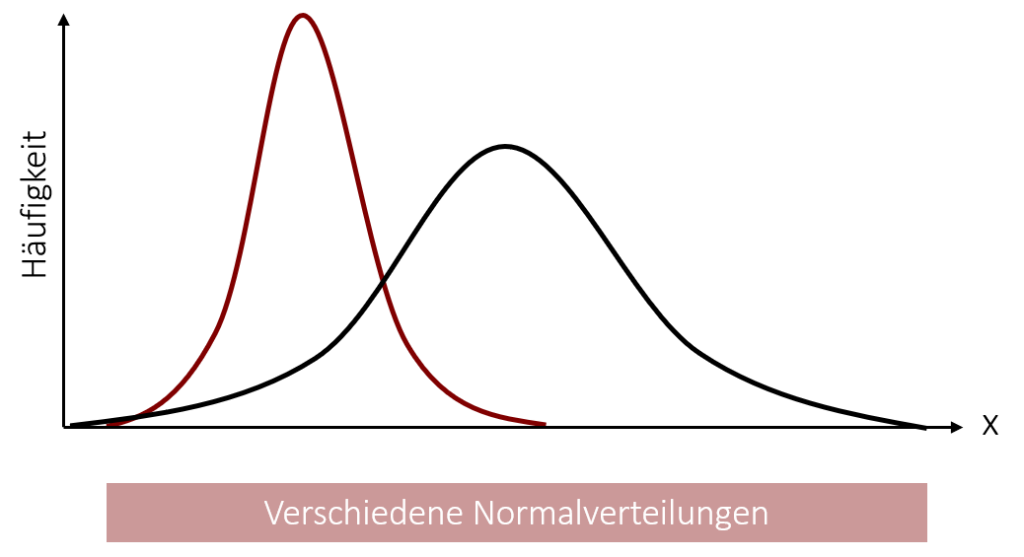
Graphisch lässt sich zeigen, dass die Standardabweichung den Abstand des Mittelwerts zum Wendepunkt einer Normalverteilung angibt. Zwischen diesen beiden Punkten liegen ca. 68%, also ca. 2/3 aller Messwerte. Hierdurch lassen sich also durchaus praktische Rückschlüsse über die Verteilung der Werte ziehen, sobald die Standardabweichung bekannt ist.
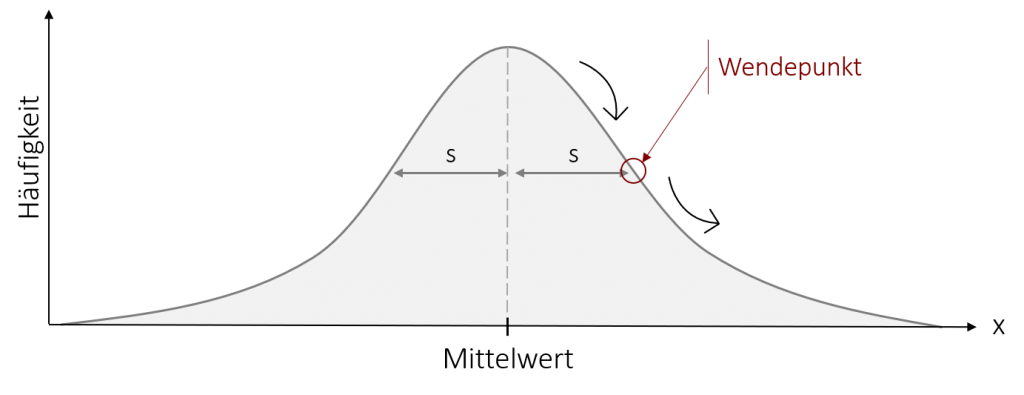
Beispiel
Expertenwissen
Im Intervall +/- einer Standardabweichung liegen exakt 68,3% der Fälle. Zwischen zwei Standardabweichungen Abstand (jeweils in beide Richtungen), liegen exakt 95,4 % der Werte.
Video 2.6 Kennwerte Streuungsmaße Standardabweichung & Normalverteilung
2.12 Übersicht Streuungsmaße
Wir haben nun gelernt, dass die Streuung einer Verteilung mit verschiedenen Kennwerten wiedergegeben werden kann. Allen gemein ist, dass sie ein Maß dafür darstellen, wie sehr die einzelnen Werte von den Werten der zentralen Tendenz abweichen. Welches ist aber nun das „beste“ Maß für die Streuung? Das hängt wieder von Ihrem Untersuchungsgegenstand ab. Für nominalskalierte Werte gibt es kein Streuungsmaß, ab ordinalskalierten Werten können Spannweite und Interquartilsabstand herangezogen werden. Ab intervallskalierten Variablen dann auch Varianz und Standardabweichung.
| Skalen- niveau |
Spann- weite |
Interquartils- abstand |
Varianz und Standard- abweichung |
| Nominal | nein | nein | nein |
| Ordinal | ja | ja | nein |
| Intervall | ja | ja | ja |
2.13 Kennwerte mit SPSS berechnen
Nachdem wir nun viele Kennwerte mühsam von Hand berechnet haben, wollen wir im Folgenden diese nun von SPSS mit wenigen Klicks berechnen lassen. Die Berechnung von Kennwerten ist oft der Einstieg in eine erste Datenanalyse. Neben dem Berechnen von Kennwerten sollten jedoch zusätzlich auch graphische Darstellungen von Verteilungen betrachtet werden (kommt im nächsten Kapitel). Grundsätzlich gibt es in SPSS verschiedene Menüs die es erlauben Lagemaße und Streuungsmaße zu berechnen. Da jedes Menü spezifische Stärken und Schwächen hat wollen wir im Folgenden drei Menüs näher betrachten.
Analysieren > Deskriptive Statistiken > Deskriptive Statistik
In diesem Menü können Sie beliebig viele Variablen zur Analyse verwenden (von links nach rechts ziehen). Mit einem Klick auf Optionen erhalten Sie eine Übersicht der zur Verfügung stehenden Kennwerte. Hier können Sie den Mittelwert (Arithmetisches Mittel), die Standardabweichung und die Varianz, sowie die Spannweite auswählen. Leider nicht vorhanden sind die Lagemaße Median und Modus. Diese finden wir im nächsten Menü.
Analysieren > Deskriptive Statistiken > Häufigkeiten
Mit diesem Menü können Sie zwei Ausgaben erzeugen: Eine Tabelle mit Kennwerte und eine Häufigkeitstabelle. Mit letzterem beschäftigen wir uns im nächsten Kapitel. Für die Kennwerte-Tabelle können Sie über den Button Statistiken die gewünschten Kennwerte auswählen. Hier finden Sie nun auch Median und Modus, sowie die Quartile, die es Ihnen erlauben den Interquartilsabstand zu berechnen. Hierfür nehmen Sie die Distanz zwischen dem 25%-Perzentil und dem 75%-Perzentil.
Analysieren > Mittelwerte vergleichen > Mittelwerte
Mit diesem Menü können Sie die Kennwerte für Variablen, getrennt nach einer weiteren (nominalen) Variable berechnen. Damit können wir zum Beispiel den Mittelwert der Variable „Schuhgröße“ berechnen, getrennt nach Männern und Frauen. Hierfür tragen Sie bei Abhängige Variable, die Variable ein, für die Kennwerte berechnet werden wollen (z.B. die Schuhgröße). Im Feld Unabhängige Variable geben Sie die Variable ein, nach der die Gruppen aufgeteilt werden sollen (z.B. Geschlecht).
Im Folgenden Video wird die Berechnung von Kennwerten mit Hilfe dieser drei Menüs nochmal erläutert.
Video 2.9 Kennwerte mit SPSS berechnen
2.14 Datenmanagement in SPSS
Im Folgenden wollen wir noch die Möglichkeiten betrachten, in SPSS Daten für die Analysen von Kennwerten vorzubereiten. Dabei sollen oft nur bestimmte Personengruppen ausgewertet werden (z.B. der Mittelwert der männlichen Personen) oder eine Variable soll vor der Analyse umgewandelt werden (z.B. in Altersgruppen).
Fälle Auswählen
Variablen umcodieren
Wenn Sie Kennwerte in R berechnen wollen, finden Sie hier des entsprechende Kapitel in meinem R-Buch.
2.15 Übungsfragen
Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!
In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!
2.16 Übungsaufgaben
Die Burgerkette Five Profs möchte zwei neue Burger einführen: den Full Harmony Burger und den Super Tasty Burger. Vorab wird eine Umfrage zu den beiden Burgern durchgeführt. Es wurden 5 Studenten gefragt, diese zwei Burger auf einer 7-stufigen Skala von -3 (= schmeckt überhaupt nicht) bis +3 (= schmeckt sehr gut) zu beurteilen. Es ergaben sich folgende Messwerte:
| Full Harmony Burger | -3 | -3 | -1 | 2 | 3 |
| Super Tasty Burger | 2 | -2 | -1 | 1 | 0 |
A Berechnen Sie den Mittelwert und Median und Varianz für beide Burger
B Berechnen Sie die Varianz und Standardabweichung für den Super Tasty Burger
Lösung A:
Lösung B:
- Pearson Karl 1894III. Contributions to the mathematical theory of evolutionPhilosophical Transactions of the Royal Society of London. (A.)18571–110 http://doi.org/10.1098/rsta.1894.0003 ↵



