Schritt 1 Vorbereitung

Notwendige Pakete Laden:

library(foreign)
library(car)
library(psych)
library(afex)
library(phia)
library(emmeans)

Wissenschaftliche Notation ausschalten (Ausser Sie mögen e+10 Notationen 🙂 )

options(scipen = 999)

Grundsätzlich empfiehlt sich für die Durchführung der ANOVA folgendes Vorgehen:

1. Eingabe / Import der Daten
2. Daten untersuchen mit deskriptiven Statistiken (Mittelwerte, Grafiken erzeugen)
3. Voraussetzungen prüfen (insb. Skalen & Varianzhomogenität, ggf. Normalität der AV in den Gruppen, wobei die ANOVA relativ robust gegen Verletzungen der Normalität ist)
4. ANOVA durchführen
5. Kontraste oder Post-Hoc Tests durchführen bzw. berechnen

Nehmen wir als Beispiel wieder an, Sie wollen die Wirksamkeit der Wunderpille testen. Dies haben wir im vorausgegangenen Kapitel mit einem t-Test gemacht. Nun wollen wir die Hypothese testen, dass zwei Pillen ein noch wirksameres Mittel sind, um die Trinkfestigkeit zu steigern.

Sie schicken dieses Mal drei Gruppen von je 10 Personen auf den Cannstatter Wasen (unabhängiges Versuchsdesign mit 3 Gruppen):

• Kontrollgruppe
• Gruppe, die eine Pille nimmt
• Gruppe, die zwei Pillen nimmt

Daten einlesen:

Trinkfestigkeit<-read.csv2(file="Trinkfestigkeit.csv")

Schritt 2 Deskriptive Unterschiede

Gibt es einen signifikanten Unterschied zwischen den 3 Gruppen? Das schauen wir uns dies zunächst deskriptiv an und erzeugen einen Boxplot.

boxplot(Trinkfestigkeit$ohnePille,Trinkfestigkeit$mitPille,Trinkfestigkeit$mit2Pillen, 
        names=c("ohne Pille","Mit Pille", "Mit 2 Pillen"))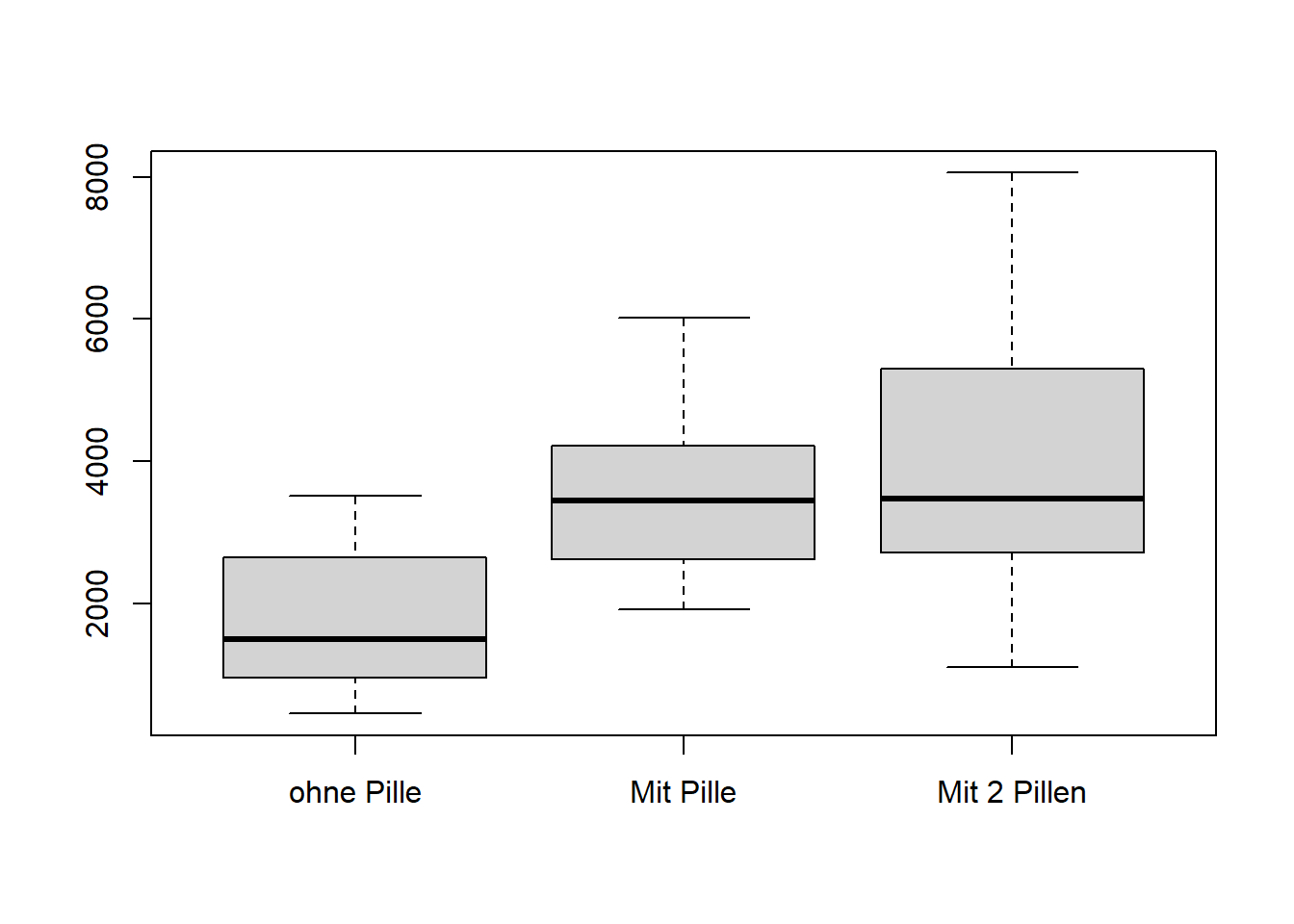

Wie man sieht, unterscheidet sich vor allem der Median ohne Pille deutlich von den anderen beiden Werten. Die Streuung scheint jedoch bei der Gruppe mit zwei Pillen am größten zu sein.

Schritt 3 Voraussetzungen prüfen

Bei der einseitigen unabhängigen ANOVA werden mehrere Annahmen über die zu analysierenden Daten getroffen. Zu diesen Annahmen gehören:

• Unabhängigkeit: Die Beobachtungen in jeder Gruppe sind unabhängig voneinander. Dies ist hier gegeben, da es drei unterschiedliche Gruppen sind.
• Skalenniveau: Die abhängige Variable muss metrisch skaliert sein. Dies ist hier gegeben (Menge in ml)
• Gleiche Varianzen: Die Varianzen der Grundgesamtheiten, aus denen die Stichproben gezogen werden, sind gleich. Dies prüfen wir nun mit dem Levene-Test.

Hinweis zur Normalität: In älteren Statistik-Büchern wird auch empfohlen auf Normalität der Residuen (seltener, der Daten) zu prüfen. Da die ANOVA jedoch relativ robust gegen Verletzungen der Normalität ist, wird diese Voraussetzung in der Regel heute nicht mehr geprüft.

Prüfen der Varianzhomogenitaet

Da der Levene-Test nur Daten im Long-Format akzeptiert, wandeln wir die Daten zunächst in das Long-Format um.

Trink.long <- stack(Trinkfestigkeit)

Nehmen wir uns die Zeit und benennen die Variablen

colnames(Trink.long) <- c("Menge","Gruppe")

So sehen die Daten nun im Long-Format aus.

head(Trink.long)
##   Menge    Gruppe
## 1   950 ohnePille
## 2  1540 ohnePille
## 3  2450 ohnePille
## 4  2650 ohnePille
## 5  1320 ohnePille
## 6   910 ohnePille

Nun führen wir den Test auf Varianzhomogenitaet durch. Die Argumente kennen Sie bereits aus dem Kapitel zum t-Test.

leveneTest(Menge ~ Gruppe, data=Trink.long) 
## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value Pr(>F)
## group  2  2.1436 0.1368
##       27

Schritt 3 ANOVA durchführen

Um eine einseitige ANOVA in R durchzuführen, können Sie die Funktion aov() verwenden. Die grundlegende Syntax für diese Funktion lautet wie folgt: aov(y ~ x, Daten) wobei y die abhängige Variable, x die unabhängige Variable (Gruppierungsvariable) und Daten der Datensatz ist.

Wenden wir dies nun auf unsere Daten an. Bei der Varianzanalyse, als auch später bei Regressionsmodellen, ist es sinnvoll, diese in einem neuen Objekt zu speichern. Sie können hier selbst einen Namen vergeben. In diesem Beispiel nennen wir das Objekt “ANOVA1”

ANOVA1 <- aov(Menge ~ Gruppe, data=Trink.long)

Nun schauen wir uns die Ergebnisse der ANOVA an. Hierzu nutzen wir die summary() Funktion und wenden diese auf unser Objekt an.

summary(ANOVA1)
##             Df   Sum Sq  Mean Sq F value  Pr(>F)   
## Gruppe       2 29481007 14740503   5.705 0.00858 **
## Residuals   27 69762730  2583805                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Wenn Sie die Funktion summary() auf ein einseitiges ANOVA-Objekt anwenden, liefert die Ausgabe mehrere wichtige Informationen, die für die Interpretation der Testergebnisse nützlich sind.

Betrachten wir zunächst die erste Zeile “Gruppe”, hier erhalten wir folgende Informationen:

• Df: Freiheitsgrade. Dies ist die Anzahl der Beobachtungen, die in der Analyse frei variieren können.
• Sum Sq: Summe der Quadrate. Sie ist ein Maß für die Gesamtvariation in den Daten.
• Mean Sq: Mittlere Quadrate. Es ist das Verhältnis der Summe der Quadrate zu den Freiheitsgraden. Diese wird verwendet, um das F-Verhältnis zu berechnen, das das Verhältnis der Varianz zwischen den Gruppen zur Varianz innerhalb der Gruppen darstellt.
• F-Wert: Der berechnete F-Wert aus dem ANOVA-Test.
• Pr(>F): Der p-Wert. Er gibt die Wahrscheinlichkeit an, dass der Mittelwertunterschied auf einen Zufall zurückzuführen ist. Ein p-Wert von weniger als 0,05 wird im Allgemeinen als statistisch signifikant angesehen.

In der zweiten Zeile “Residuals” werden die Differenzen zwischen den beobachteten Werten (den tatsächlichen Testergebnissen) und den vorhergesagten Werten (den Testergebnissen, die zu erwarten wären, wenn die Nullhypothese wahr wäre) angezeigt. Diese Residuen werden zur Berechnung der gruppeninternen Varianz verwendet, die ein Maß für die Variation innerhalb jeder Gruppe ist.

In der letzen Zeile werden die Signifikanzcodes erläutert. Dies ist nur eine Legende und daher immer gleich. Signifikanzcodes werden verwendet, um die Signifikanz der Ergebnisse schnell zu erkennen. Liegt der p-Wert beispielsweise unter 0,05, wird er mit “*” angegeben, was auf einen signifikanten Unterschied der Mittelwerte zwischen den Gruppen hinweist. .

In diesem Fall wird die ANOVA signifikant, das bedeutet, dass sich mindestens zwei Gruppen signifikant unterscheiden. Bei der Interpretation der Ergebnisse einer einseitigen unabhängigen ANOVA ist zu beachten, dass ein signifikanter Unterschied in den Mittelwerten nicht unbedingt bedeutet, dass sich alle Gruppen unterscheiden. Es bedeutet lediglich, dass ein signifikanter Unterschied in den Mittelwerten mindestens bei zwei untersuchten Gruppen besteht. Daher müssen wir im nächsten Schritt noch eine sogenannte Post-Hoc Analyse durchführen, um zu ermitteln, zwischen welchen der drei Gruppen signifikante Unterschiede bestehen.

Hinweis zur Verletzung der Voraussetzungen:

Wenn die Voraussetzung der Varianzhomogenität verletzt ist (also Varianzheterogenität vorliegt) kann eine ANOVA mit der oneway.test Funktion durchgeführt werden. Diese beinhaltet eine Welch-Korrektur.

oneway.test(Menge ~ Gruppe, data=Trink.long)
## 
##  One-way analysis of means (not assuming equal variances)
## 
## data:  Menge and Gruppe
## F = 7.8096, num df = 2.000, denom df = 16.775, p-value =
## 0.004007

In diesem Video zeige ich, wie das in R funktioniert:

Alternativ bietet sich für die Durchführung der Varianzanalyse auch das afex-Paket an. Dieses bietet insbesondere Vorteile für die Interpretation der mehrfaktoriellen ANOVA im nächsten Schritt, kann aber auch bei der einfaktoriellen ANOVA angewendet werden. Die ANOVA Funktion in afex nennt sich aov_car. Die Notation entspricht dem oben beschriebenen Vorgehen bei der aov Funktion, nur dass zusätzlich noch ein Error-Term definiert werden muss, der sich auf eine ID-Variable beziehen muss. Dies ist eine Variable, die jedem Versuchsteilnehmer eine eindeutige Nummer zuweist und ist insbesondere bei Messwiederholungs-Daten unerlässlich. Unser kleiner Datensatz hat diese fortlaufende Nummer jedoch leider nicht, daher müssen wir diese zuerst generieren:

Trink.long$ID <- c(1:30)

Dann laden wir das Paket und führen die ANOVA durch. Das neue Objekt nennen wir “ANOVA1A”.

ANOVA1A <- aov_car(Menge ~ Gruppe + Error(ID), data=Trink.long)
## Contrasts set to contr.sum for the following variables: Gruppe
summary(ANOVA1A)
## Anova Table (Type 3 tests)
## 
## Response: Menge
##        num Df den Df     MSE     F     ges   Pr(>F)   
## Gruppe      2     27 2583805 5.705 0.29706 0.008579 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Der Output enstpricht in diesem Fall 1:1 dem Output, den wir zuvor mit der aov Funktion generiert haben (mit der Ausnahme, dass keine Residuen angezeigt werden). Daher entspricht die Interpretation der obigen.

In diesem Video zeige ich, wie das in R funktioniert:

Schritt 4 Post-Hoc Verfahren

Jetzt wissen wir, dass es einen Einfluss auf die Trinkfestigkeit gibt. Aber noch nicht welchen. Hierfür benötigen wir sog. Post-hoc-Tests, um festzustellen, welche spezifischen Gruppenpaare für einen signifikanten Unterschied in den Mittelwerten verantwortlich sind, wenn ein einseitiger ANOVA-Test einen signifikanten Unterschied ergibt. Post-hoc-Tests werden üblicherweise nur nach einem signifikanten ANOVA-Ergebnis angewendet. Es gibt mehrere verschiedene Post-hoc-Tests, die für die einseitige ANOVA verwendet werden können, darunter der Tukey-HSD-Test, der Scheffé-Test und der Bonferroni-Test.

Post-Hoc-Tests

Wir machen nun paarweise t-Tests, um zu ermitteln, welche Gruppen sich signifikant unterscheiden. Bei mehreren t-Tests mit derselben Stichprobe muss aufgrund der Alpha-Fehler-Inflation eine Korrektur vorgenommen werden. Mit zunehmender Anzahl der Vergleiche steigt auch die Wahrscheinlichkeit eines Alpha-Fehlers, was zu einem erhöhten Risiko falsch positiver Ergebnisse führen kann. Die Bonferroni-Korrektur ist eine Methode zur Kontrolle der Alpha-Fehler-Inflation durch Anpassung der p-Wert-Schwelle für die Signifikanz.

Die Korrektur ist dabei recht einfach: Bei der Bonferroni-Korrektur wird das Signifikanzniveau (Alpha) durch die Anzahl der durchgeführten Vergleiche geteilt, wodurch ein konservativerer Schwellenwert für die Signifikanz entsteht. Wenn beispielsweise das Signifikanzniveau auf 0,05 festgelegt ist und 10 Vergleiche durchgeführt werden, würde die Bonferroni-Korrektur 0,05 durch 10 teilen, was ein neues Signifikanzniveau von 0,005 ergibt.

Hierzu nutzen wir die Funktion pairwise.t.test mit dem Argument p.adj=“bonferroni”.

pairwise.t.test(Trink.long$Menge, Trink.long$Gruppe, p.adj="bonferroni")
## 
##  Pairwise comparisons using t tests with pooled SD 
## 
## data:  Trink.long$Menge and Trink.long$Gruppe 
## 
##            ohnePille mitPille
## mitPille   0.047     -       
## mit2Pillen 0.011     1.000   
## 
## P value adjustment method: bonferroni

Wir sehen nun also, dass sich bei Einnahme einer Pille, die Trinkfestigkeit signifikant erhöht (p = .047) und bei der Einnahme von zwei Pillen, dies Trinkfestigkeit ebenfalls signifikant steigt (p = .011) im Vergleich zur Kontrollgruppe ohne Pille. Jedoch gibt es keinen signifikanten Unterschied zwischen den Gruppen die eine und zwei Pillen genommen haben (p = 1), daher kann keine Empfehlung für das nehmen einer weiteren Pille ausgesprochen werden.

Hinweis: Im Falle von Varianzheterogenität sollte zusätzlich das Argument pool.sd=FALSE aufgenommen werden

pairwise.t.test(Trink.long$Menge, Trink.long$Gruppe, p.adj="bonferroni",pool.sd=FALSE)
## 
##  Pairwise comparisons using t tests with non-pooled SD 
## 
## data:  Trink.long$Menge and Trink.long$Gruppe 
## 
##            ohnePille mitPille
## mitPille   0.012     -       
## mit2Pillen 0.030     1.000   
## 
## P value adjustment method: bonferroni

Es ist wichtig zu beachten, dass die Bonferroni-Korrektur eine sehr konservative Methode ist, die dazu neigt, die Typ-II-Fehlerrate zu erhöhen (eine falsche Nullhypothese wird nicht zurückgewiesen), und sie ist möglicherweise nicht geeignet, wenn die Anzahl der Vergleiche groß ist. Andere Methoden wie die Tukey sind hier gute Alternativen, da sie die Typ-II-Fehlerrate nicht so stark erhöhen.

Tukey’s HSD Test

Der Tukey-HSD-Test (Honestly Significant Difference) ist ein weiterer Post-hoc-Test. Der Test vergleicht alle möglichen Paare von Gruppenmittelwerten und berechnet einen Bereich von Unterschieden, die als statistisch signifikant angesehen werden, die sogenannten HSD-Intervalle. Liegt der Unterschied zwischen den Mittelwerten zweier Gruppen außerhalb dieses Intervalls, wird er als statistisch signifikant angesehen und die Gruppen werden als unterschiedlich betrachtet.

Der Test ist recht einfach ausgeführt.

TukeyHSD(ANOVA1) 
##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = Menge ~ Gruppe, data = Trink.long)
## 
## $Gruppe
##                      diff         lwr      upr     p adj
## mitPille-ohnePille   1854    71.64362 3636.356 0.0402560
## mit2Pillen-ohnePille 2285   502.64362 4067.356 0.0099925
## mit2Pillen-mitPille   431 -1351.35638 2213.356 0.8215272

Alternativ zum Tukey’s HSD Test können mit dem emmeans Paket und gleichnamiger Funktion tuckey-korrigierte Paarvergleiche abgerufen werden. Hierzu muss immer die unabhängige Variable (also die Gruppierungsvariable) mit dem Befehl specs in Anführungszeichen angegeben werden. Die Ergebnisse können dann am besten mit der pairs Funktion ausgegeben werden (Für den Paarvergleich).

ph1 <- emmeans(ANOVA1, specs="Gruppe")
pairs(ph1)
##  contrast               estimate  SE df t.ratio p.value
##  ohnePille - mitPille      -1854 719 27  -2.579  0.0403
##  ohnePille - mit2Pillen    -2285 719 27  -3.179  0.0100
##  mitPille - mit2Pillen      -431 719 27  -0.600  0.8215
## 
## P value adjustment: tukey method for comparing a family of 3 estimates

Eine weitere Alternative wären geplante Kontraste. Hiermit können gezielte Gruppenvergleiche hergestellt werden, was noch sensitivere Ergebnisse ermöglicht, falls es bereits spezielle Hypothesen gibt. Diese werden an dieser Stelle jedoch nicht weiter vertieft.

In diesem Video zeige ich, wie das in R funktioniert:

Schritt 5 Grafische Verfahren

Bei der Ergebnisdarstellung einer ANOVA bieten sich grundsätzlich grafische Darstellungen an. Dies wird später bei mehrfaktoriellen Designs besonders spannend (Interaktionsdiagramm), kann aber auch schon bei einer einfaktoriellen ANOVA genutzt werden.

Plot aus dem Paket “phia” mit der Funktion „Interaction Means“. Wichtiger Hinweis: Diese Funktion erstellt standardmäßig Fehlerbalken mit einem Standardfehler. Wenn Sie diese mit dem üblichen 95% Konfidenzintervall erstellen wollen, müssen Sie die „plot“ Funktion noch um das Argument errorbar=“ci95″ ergänzen.

plot(interactionMeans(ANOVA1))

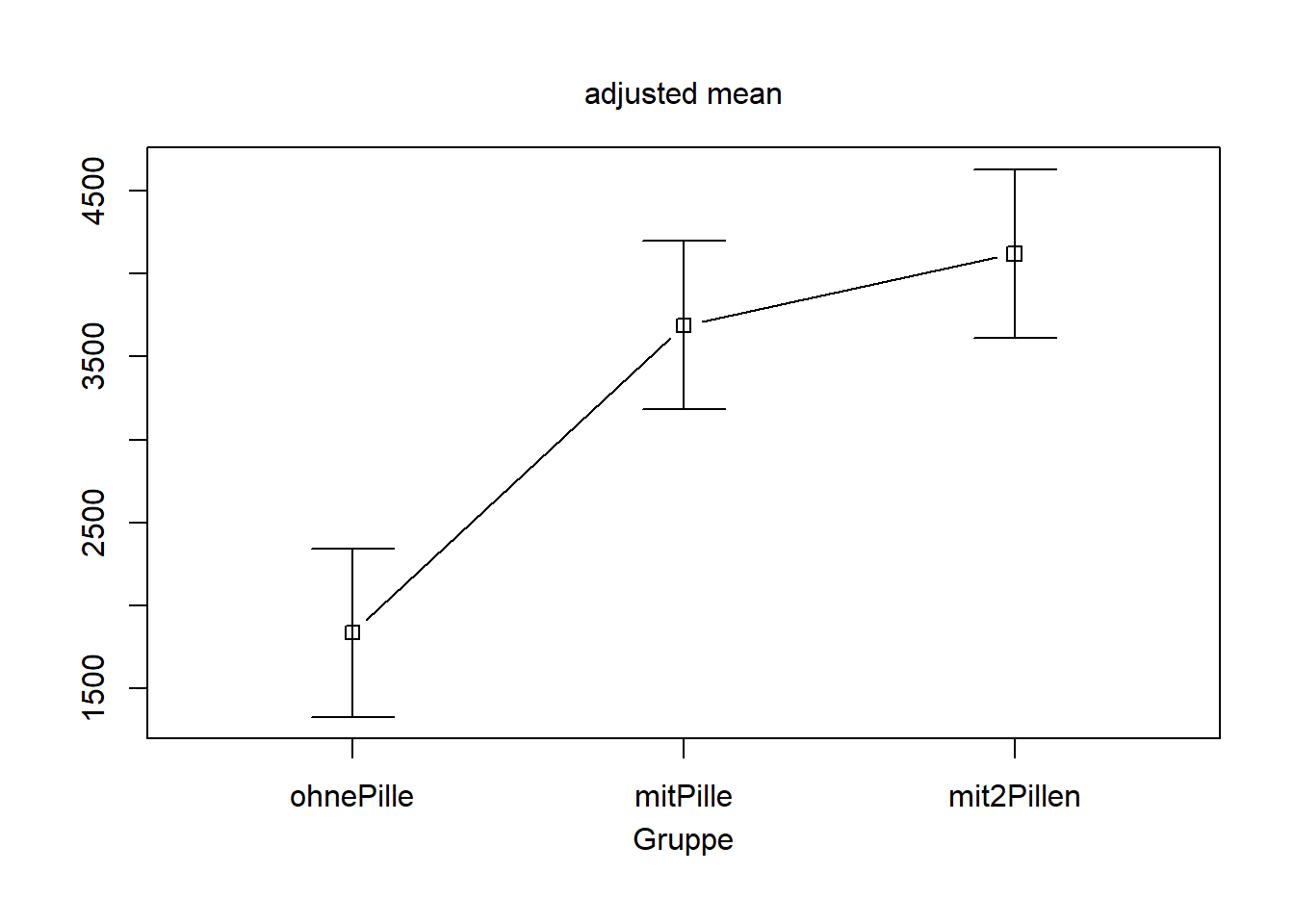
Alternativ kann mit der Funktion afex_plot aus dem afex Paket eine schönere Grafik erzeugt werden, die auf GGPlot2 basiert und direkt das 95% Konfidenzintervall ausgiebt.

afex_plot(ANOVA1A, x="Gruppe")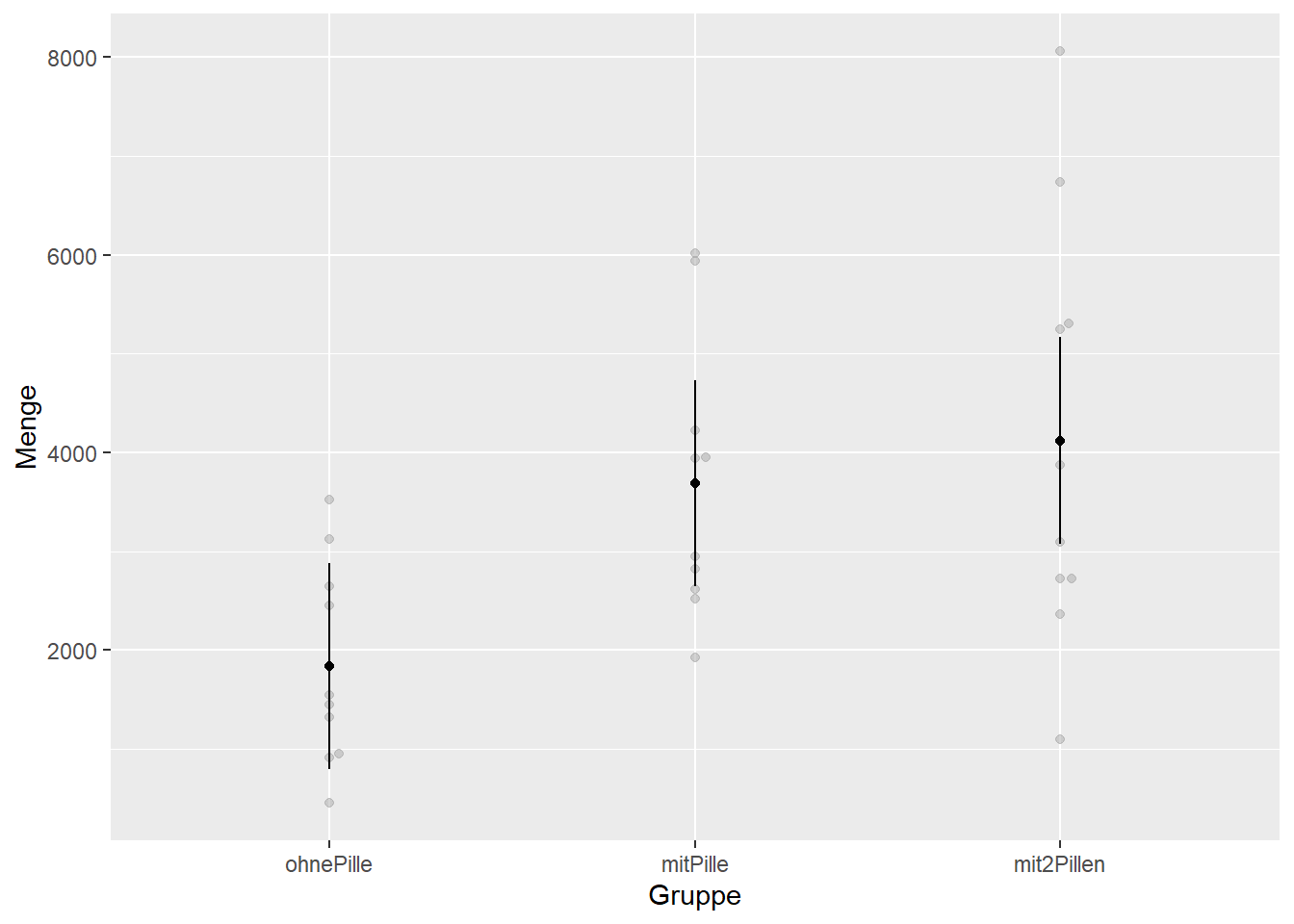

Die Darstellung ist ein Fehlerbalken-Diagramm mit den Mittelwerten und Standardabweichungen der Gruppen, wobei die Mittelwerte durch die Punkte und die Standardabweichungen durch die Boxplots selbst dargestellt sind. Zu sehen sind ausserdem (in hellerem Grau) auch die Rohdaten.

Übung

Wir wollen die Wirksamkeit von Diäten vergleichen. Wir haben ein Datenset (diet3.csv) von 78 Personen, die jeweils eine von 3 Diäten durchlaufen haben. Wir haben das Gewicht vor der Diät, das Gewicht nach der Diät, die Variable “weightlost”, die Ihnen die Gewichtsabnahme (Zunahme) in Pfund angibt und einige Hintergrundinformationen.

Vergleichen Sie die 3 Diäten im Hinblick auf ihre Wirksamkeit (AV ist “weightlost”).

Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.

Übung

Wir wollen wissen, ob sich das Besucheraufkommen auf der Stuttgarter Königstrasse (Koenig_Mitte) signifikant zwischen den Wochentagen (Tag) unterscheidet.

Hierzu haben wir im Kapitel “Grafiken” folgenden plot erzeugt:
Daten einlesen:

library(readxl)
Passanten <- read_excel("Passanten2019.xlsx")

Plot:

Passanten$Tag <- as.factor(Passanten$Tag)
Passanten$Tag <- ordered(Passanten$Tag,levels=c("Mo","Di","Mi","Do","Fr","Sa","So"))
plot(Passanten$Koenig_Mitte~Passanten$Tag)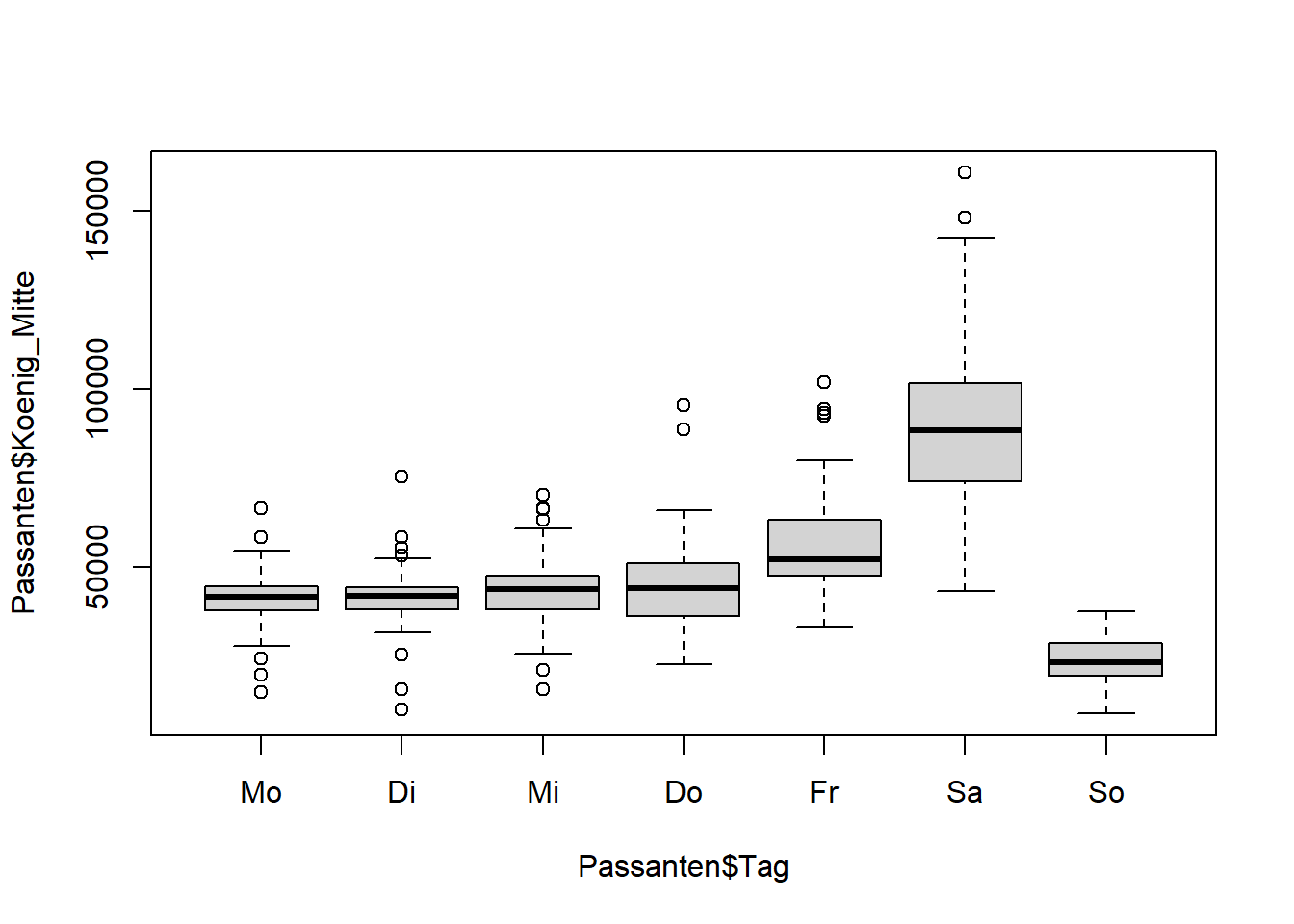

Vergleichen Sie die Wochentage, welche unterscheiden sich signifikant?

Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.