Hypothesentests
13 Rangsummentest
13.0 Einführung Rangsummentest
In diesem Kapitel widmen wir uns der Testung von Unterschiedshypothesen. Diese versuchen die Frage zu beantworten, ob zwischen zwei oder mehreren Populationen ein Unterschied besteht bzw. ob sich zwei oder mehrere Populationen bezüglich einer (oder mehrerer) Variablen unterscheiden. Damit lassen sich beispielweise Fragen beantworten wie: „Essen BWL-Studierende mehr Burger als Jura-Studierende?“ oder „Ist unsere ’spicy‘ Burgersauce geschmacklich überzeugender als unsere ’sweet‘ Burgersauce?“. Durch den Vergleich von zwei Gruppen, können somit Aussagen über folgende Forschungshypothesen getroffen werden:
H0: Es gibt keinen Unterschied zwischen den Testgruppen
H1: Es gibt einen Unterschied zwischen den Testgruppen (ungerichtete Hypothese)
Die Testgruppen, die auf einen Unterschied hin überprüft werden sollen, können hierbei unabhängig oder abhängig voneinander sein. Je nachdem welcher Fall vorliegt, werden andere statistische Tests in der Auswertung hinzugezogen. Im Fall unserer Burgersaucen haben wir beispielsweise abhängige Stichproben, wenn unsere Geschmackstester in einem Test beide Burgersauce bewerten sollen und diese Ratings miteinander verglichen werden. Beurteilt hingegen eine Gruppe die ’spicy‘ Sauce und eine andere die ’sweet‘ Sauce, sind beide Gruppen unabhängig voneinander. In diesem Kapitel schauen wir uns den zweiten Fall, also eine Testung von zwei unabhängigen Gruppen, genauer an. Für unabhängige Gruppen existieren eine Reihe von Tests, die sich bezüglich ihrer Voraussetzungen, wie beispielsweise dem Skalenniveau der abhängigen Variable, unterscheiden.
| Skala der abhängigen Variable | Mögliche Tests für unabhängige Stichproben |
| Dichotom | Vierfelder Chi-Quadrat-Test |
| Nominal | Mehrfelder Chi-Quadrat-Test |
| Ordinal | Mann-Whitney-U-Test
Rangsummentest (Wilcoxon) |
| Intervall | t-Test für unabhängige Stichproben
Welch-Test |
Den Chi-Quadrat-Test haben Sie bereits im letzten Kapitel kennengelernt. In diesem Kapitel widmen wir uns hingegen den statistischen Tests, die man im Falle von Ordinaldaten verwendet. Nochmal zur Erinnerung: Die Ausprägungen von ordinalen Variablen lassen sich in eine klare Rangfolge bringen, jedoch kann man über die Abstände zwischen den einzelnen Ausprägungen keine Aussage treffen. Besonders im Bereich der Marktforschung sind viele Antwortskalen und damit auch die abhängige Variablen im strengen Sinne ordinalskaliert, obwohl sie oftmals als intervallskaliert betrachtet werden. So auch in unserem Beispiel der Burgersaucen. Nehmen wir an, wir möchten unsere Burgersauce „sweet“ mit unserer „spicy“ Burgersauce vergleichen. Hierfür führen wir mit unseren Kunden ein Geschmackstest durch, in dem sie eine der beiden Burgersaucen auf einer 4-stufigen Skala bewerten können.
Die Bürgersauce schmeckt…
| ☐ | ☐ | ☐ | ☐ |
| schlecht | herkömmlich | gut | herausragend |
Um den Geschmack der beiden Saucen anschließend auf signifikante Unterschiede zu überprüfen, müssen wir einen Test für zwei unabhängige Stichproben durchführen. In unserem Fall haben wir ordinalskalierte Daten und können somit den Rangsummentest nach Wilcoxon oder den Mann-Whitney-U-Test wählen. Bei den beiden Verfahren handelt es sich um verteilungsfreie (oder nicht parametrische) Tests, die keine bestimmte Verteilungsform voraussetzen und die Hypothese überprüfen, ob sich zwei unabhängige Gruppen hinsichtlich ihrer zentralen Tendenz unterscheiden. Ihre Hypothesen lauten:
H0: Es gibt keinen Unterschied zwischen beiden Testgruppen hinsichtlich ihrer zentralen Tendenz
H1: Es gibt einen Unterschied zwischen beiden Testgruppen hinsichtlich ihrer zentralen Tendenz (ungerichtete Hypothese)
Welchen der beiden Tests man durchführt, ist dabei nicht entscheidend, da beide Tests über die gleichen Eigenschaften verfügen und sich in ihren Ergebnissen nicht unterscheiden. Aufgrund dieser Äquivalenz werden sie gemeinsam auch als Wilcoxon-Mann-Whitney-Test bezeichnet.
Ihre zugrundeliegende Idee besteht darin, dass sie für den Vergleich der beiden Testgruppen nicht das Maß der zentralen Tendenz (hierbei wäre das der Median) sondern Rangsummen betrachten, die aus den Rängen der Merkmalsausprägungen berechnet werden. Diese Rangsummen können als Pendant zum Mittelwert aufgefasst werden. Jedoch berücksichtigen Rangsummen im Gegensatz zum Mittelwert keine Informationen über die tatsächlichen Abstände zwischen den Messwerten, wodurch den Tests oft eine geringere Power (Teststärke) unterstellt wird. Da wir jedoch ohnehin Ordinaldaten vorliegen haben, existieren diese Informationen über die Abstände nicht und sollte daher auch nicht in die Berechnung eines Tests einfließen.
Aus diesem Grund werden in beiden Tests die Prüfgrößen nicht aus den jeweiligen Messwerten, sondern aus deren Rangzahlen berechnet. Am Ende erhalten wir bei beiden Verfahren einen empirischen z-Wert, den wir, wie bereits im Kapitel z-Test/Gaußtest, mit unserem kritischen z-Wert vergleichen und so die Nullhypothese ablehnen oder bestätigen können.
Doch wie sieht die Berechnung in der Praxis aus? Und wie kann ich aus meinen Daten Rangsummen bilden? Schauen wir uns die beiden Tests am Beispiel von Burgersaucen an.
Falls Sie das Thema noch anhand eines weiteren Beispiels aus der FiveProfs-Kette nachvollziehen wollen, können Sie sich zudem das folgende Video begleitend anschauen.
13.1 Rangsummentest für Ordinaldaten | Einführung
13.1 Voraussetzungen der Rangsummentests
Hypothesen aufstellen
Vor der eigentlichen Testung auf signifikante Unterschiede bilden wir zunächst unsere Forschungshypothesen. Die allgemeinen Forschungshypothesen des Rangsummentests nach Wilcoxon sowie des Mann-Whitney-U-Test haben Sie bereits im letzten Abschnitt kennengelernt. Bezogen auf unser Burgersaucen-Beispiel lauten unsere Hypothesen wie folgt:
H0: Es gibt keinen Unterschied zwischen der „spicy“ und der „sweet“ Sauce im durchschnittlichen Geschmacksempfinden.
H1: Es gibt einen Unterschied zwischen der „spicy“ und der „sweet“ Sauce im durchschnittlichen Geschmacksempfinden.
In unserem Beispiel testen wir eine ungerichtete Hypothese. Grundsätzlich können die Tests auch für gerichtete Hypothesen durchgeführt werden, jedoch benötigen wir in diesen Fällen einschlägiges Vorwissen, auf welches wir unsere Vermutung stützen können.
Voraussetzungen überprüfen
Nachdem die Forschungshypothesen aufgestellt sind und der entsprechende Test ausgewählt wurde, müssen anschließend die Voraussetzungen überprüft werden, bevor es an die eigentliche Testung geht. Die Voraussetzungen für den Rangsummentest nach Wilcoxon sowie den Mann-Whitney-U-Test sind:
- Die abhängige Variable muss mindestens ordinalskaliert sein.
- Es müssen zwei voneinander unabhängige Stichproben vorliegen.
Im Beispiel sind alle Voraussetzungen erfüllt, sodass wir zum nächsten Schritt übergehen können – der Berechnung der Rangsummen.
Exptenwissen: Rangsummentest als verteilungsfreie Alternative zum t-Test
Oftmals werden die Rangsummentests auch für intervallskalierte Daten verwendet, falls die Voraussetzungen für die entsprechenden Test für intervallskalierte Daten (z.B. Normalverteilung der Daten) nicht gegeben sind. Aus diesem Grund sind die Rangsummen-Tests auch als die verteilungsfreie Alternative zum t-Test für unabhängige Stichproben (welchen wir später behandeln) bekannt.
13.2 Berechnung der Rangsummen
Bevor es an die Berechnung der Rangsummen geht, vergegenwärtigen wir uns noch einmal unser Beispiel: Wir möchten herausfinden, ob sich unsere Burgersaucen „spicy“ und „sweet“ geschmacklich unterscheiden und ob vielleicht eine der beiden besser schmeckt. Hierfür lassen wir unsere „spicy“ Sauce von 7 und unsere „sweet“ Sauce von 8 FiveProfs Kunden testen und bewerten. Ihre Bewertungen wurden in der nachfolgenden Tabelle zusammengetragen:
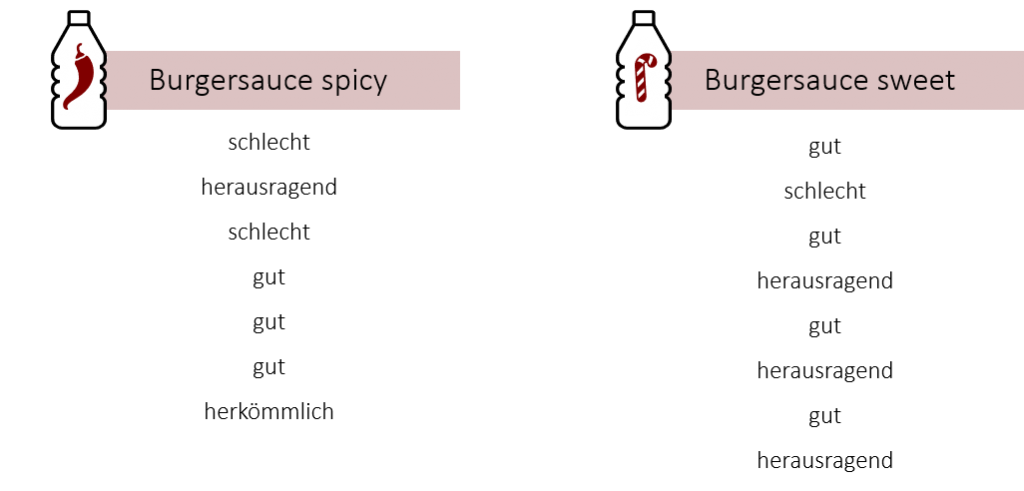
Nun möchten wir für jede Testgruppe die Rangsumme berechnen, um die beiden Saucen anschließend auf Unterschiede testen zu können.
1. Schritt: Daten beider Stichproben in eine Rangreihe bringen
Im ersten Schritt werfen wir beide Stichproben „in einen Topf“ und erstellen aus unseren zwei anfänglichen Listen eine Gesamtliste. In ihr sortieren wir unsere Daten entweder aufsteigend oder absteigend nach ihren Ausprägungen und erstellen somit eine gemeinsame Rangreihe. Tipp: Wenn Sie neben den einzelnen Ausprägungen die jeweiligen Stichproben notieren, aus denen sie stammen, können Sie diese anschließend schneller wieder den beiden Gruppen zuordnen. In unserem Beispiel erhalten wir so folgende sortierte Gesamtliste:

2. Schritt: Rangplätze bilden
Als nächstes bestimmen wir für jeden Messwert einen Rang. Hierfür „nummerieren“ wir unsere bestehende Rangreihe durch und schreiben neben dem jeweiligen Messwert einen entsprechenden Rangplatz von 1 bis n. Ob Sie hierbei die Ränge aufsteigend oder absteigend vergeben, bleibt Ihnen überlassen. Sie sollten sich Ihre Rang-Logik dennoch merken, da sich aus ihr die späteren Rangsummen berechnen. In unserem Beispiel repräsentieren kleinere Ränge (und demensprechend kleinere Rangsummen) eine schlechtere Geschmacksbewertung der Kunden:

3. Schritt: verbundene Ränge bilden
Bei gleichen Werten müssen verbundene Ränge gebildet werden, da zwei gleiche Messwerte nicht als zwei verschiedene Ränge gewertet werden sollten. Beispielsweise sollte die Bewertung „gut“ immer den gleichen Rang erhalten. Um diese verbundenen Ränge zu berechnen, bilden wir den Mittelwert aus den Rangplätzen der selben Messwerte. Anders gesagt vergeben wir für alle gleichen Ausprägungen jeweils den mittleren Rang aller dieser Ausprägung zugeordneten Ränge. So erhalten am Ende gleiche Geschmacksbewertungen auch den selben Rangplatz.
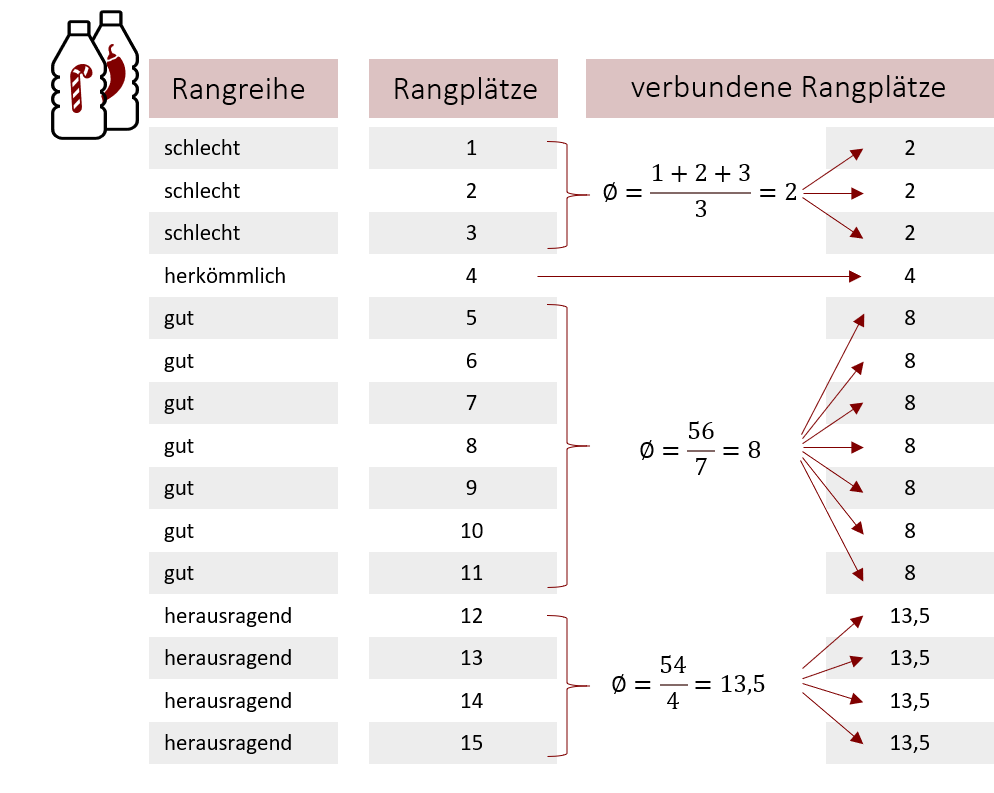

4. Schritt: Errechnen der Rangsumme für die jeweilige Stichprobe
Nachdem die Rangplätze feststehen, teilen wir unsere stichprobenübergreifende Rangreihe wieder in die einzelnen Stichproben auf und bilden somit unsere anfänglichen Listen – nur diesmal mit den dazugehörigen Rängen. Anschließend summieren wir die Ränge in beiden Gruppen auf, sodass wir die jeweilige Rangsumme erhalten.

Wir sehen, dass die Burgersauce „sweet“ eine deutlich höhere Rangsumme aufweist als unsere Burgersauce „spicy“. Dieser Unterschied ergibt sich einerseits aus den verschiedenen Messwerten, jedoch auch durch die unterschiedlichen Gruppengrößen der beiden Stichproben. So scheint es nur logisch, dass die Testgruppe „Burgersauce sweet“ aufgrund ihrer größeren Probandenanzahl eine höhere Rangsumme aufweist. Um die Rangsummen der Gruppen vergleichbar zu machen, müssen wir deshalb die durchschnittlichen Rangsummen berechnen.
5. Schritt: Berechnung der durchschnittlichen Rangsummen
Zur Berechnung der durchschnittlichen Rangsummen teilen wir unsere eben errechneten Rangsummen durch die jeweilige Stichprobengröße.
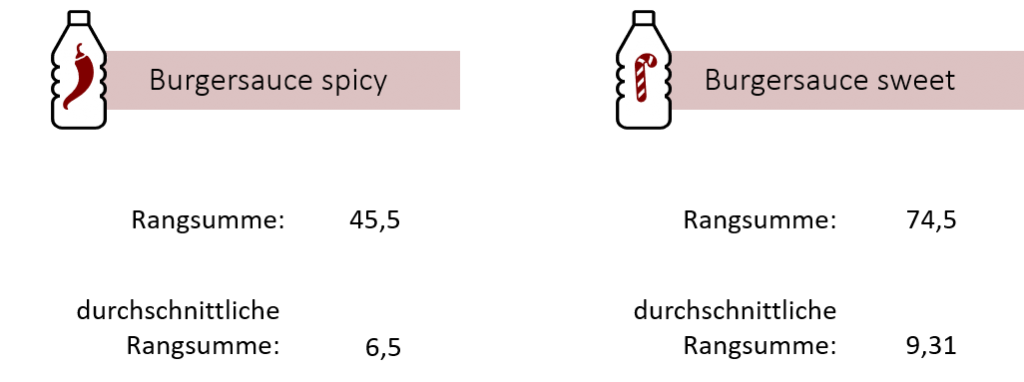
Nun können wir unsere beiden Burgersaucen im Hinblick auf ihren Geschmack vergleichen. Zur Erinnerung: Je besser die Sauce geschmeckt hat, desto höher war der Rang, der vergeben wurde. Dementsprechend bedeutet eine höhere durchschnittliche Rangsumme, dass die Sauce den befragten Kunden besser geschmeckt hat. In unserem Fall hat die Burgersauce „sweet“ deutlich besser abgeschnitten als die Sauce „spicy“. Doch ist dieser deskriptive Unterschied nur das Ergebnis eines Zufalls oder handelt es sich hierbei um eine statistisch signifikante Diskrepanz zwischen den beiden Stichproben? Um dies herauszufinden, können Sie sowohl den Rangsummentest nach Wilcoxon als auch den Man-Whitney-U-Test durchführen. Beide Tests sind statistisch gleichwertig und unterscheiden sich in ihrem Ergebnis nicht. Beginnen wir zunächst mit dem Rangsummentest nach Wilcoxon.
Falls noch einige Fragen zur Bildung von Rangsummen offengeblieben sind, veranschaulicht Ihnen das folgende Video die Berechnung anhand eines weiteren Beispiels aus der FiveProfs Kette.
13.2 Rangsummentest für Ordinaldaten | Berechnung der Rangsummen
13.3 Rangsummentest nach Wilcoxon
Der Rangsummentest nach Wilcoxon überprüft, ob es einen signifikanten Unterschied zwischen zwei unabhängigen Stichproben gibt. In unserem Burgersaucen-Beispiel kann er somit feststellen, ob der deskriptiv gefundene Unterschied zwischen den Saucen signifikant ist und auf die Kunden der FiveProfs-Kette verallgemeinert werden kann. Um ihn durchzuführen, ermitteln wir, wie bereits bei unseren vorherigen Testverfahren, zunächst die Prüfgröße. Bei kleinen Stichprobengrößen entspricht die Prüfgröße Ws der kleineren Rangsumme der beiden Stichproben. In unserem Beispiel erhalten wir so eine Prüfgröße von Ws= 45,5, was der Rangsumme der Burgersauce „spicy“ entspricht. Dieser empirische Wert wird anschließend mit dem kritischen Wert aus den entsprechenden Tabellen für den Rangsummentest nach Wilcoxon verglichen.
Bei größeren Stichproben mit n>20 (wobei die Mindestgröße in der Literatur zwischen 12 und 50 stark schwankt) ist die Prüfstatistik hingegen annähernd normalverteilt, sodass wir in diesen Fällen unsere Prüfgröße in einen z-Wert umrechnen können. Hierzu führen wir mit der Prüfgröße Ws eine z-Transformation durch:
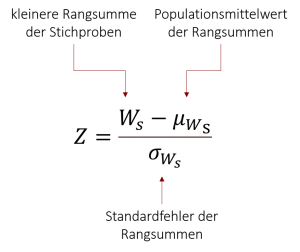
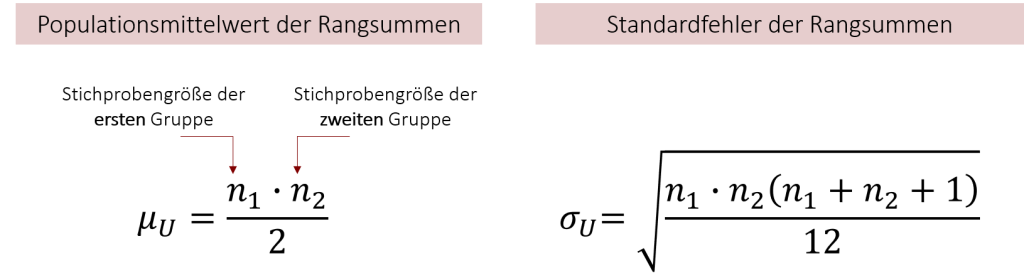
Die Formel vergleicht die empirische Rangsumme Ws mit der erwarteten Rangsumme unter Annahme der Nullhypothese. Ws haben wir bereits im letzten Abschnitt berechnet und für unser Beispiel einen Wert von Ws= 45,5 erhalten. Um nun den entsprechenden z-Wert zu errechnen, benötigen wir den Mittelwert und den Standardfehler der Normalverteilung, die für den vorliegenden Fall geschätzt (approximiert) wird. Bei der Normalverteilung handelt es sich jedoch nicht wie beim z-Test um die Normalverteilung der Mittelwerte. Hierbei betrachten wir stattdessen die Normalverteilung der Differenzen zwischen den Rangsummen der beiden Stichproben. Dessen Parameter lassen sich durch folgende Formeln berechnen:
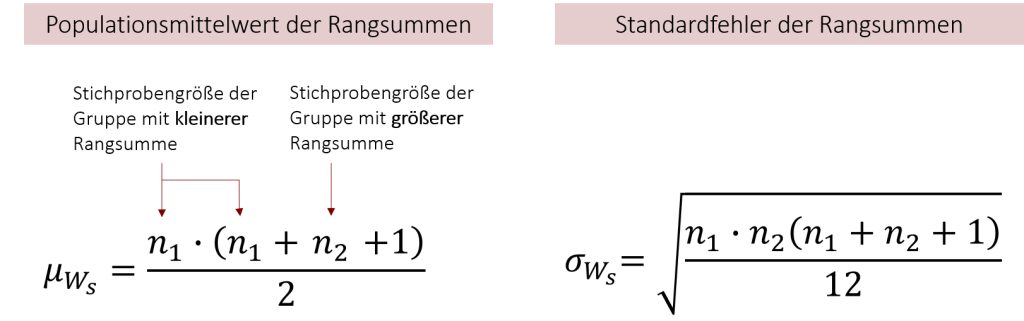
Um Ihnen die Berechnung dieser Formeln zu veranschaulichen, behalten wir unser bisheriges Burgersaucen-Beispiel bei, obwohl eine Approximation in die Normalverteilung streng genommen erst ab höheren Stichprobengrößen möglich ist. In unserem Beispiel war die Stichprobengröße der kleineren Rangsumme n1=7, die andere Gruppe hatte eine Größe von n2=8. Setzen wir dies in die Formeln ein, ergibt sich folgender z-Wert:
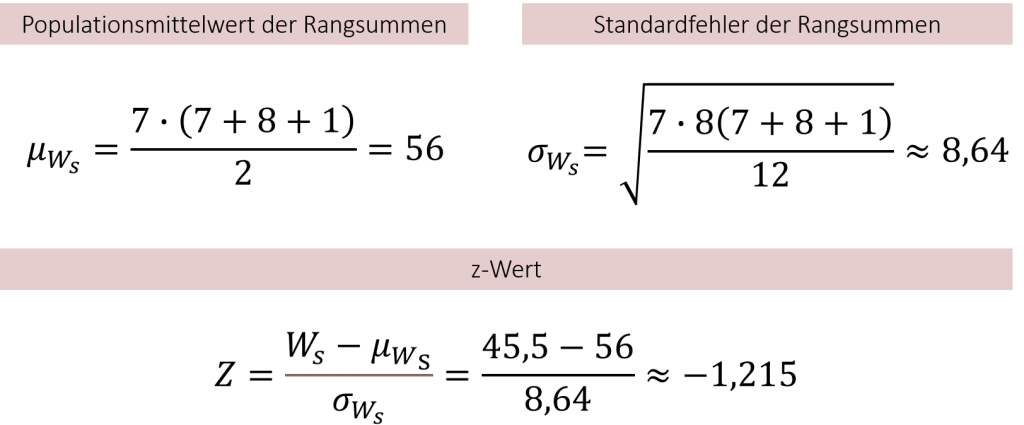
Um diesen z-Wert von -1,215 interpretieren und damit unsere Ausgangsfragestellung beantworten zu können, ob sich die Burgersaucen geschmacklich signifikant unterscheiden, vergleichen wir unseren errechneten z-Wert mit dem entsprechenden kritischen z-Wert, welchen wir aus den uns bekannten Normalverteilungstabellen ablesen können. Doch bevor wir dies tun, werfen wir einen Blick auf den äquivalenten Mann-Whitney-U-Test und wie man seine Prüfgröße berechnet.
Das folgende Video bietet Ihnen die Möglichkeit, die Berechnung des Rangsummentests nach Wilcoxon anhand eines weiteren Beispiels aus der FiveProfs-Kette nachzuvollziehen.
13.3 Rangsummentest für Ordinaldaten | Wilcoxon Test
13.4 Mann-Whitney-U-Test
Ebenso wie beim Rangsummentest nach Wilcoxon müssen wir auch beim Mann-Whitney-U-Test zunächst die Prüfgröße – in diesem Fall ist es die Prüfgröße U – berechnen, um unsere Stichproben auf signifikante Unterschiede testen zu können. Hierfür bestimmen wir für beide Testgruppen jeweils einen U-Wert nach folgender Formel:
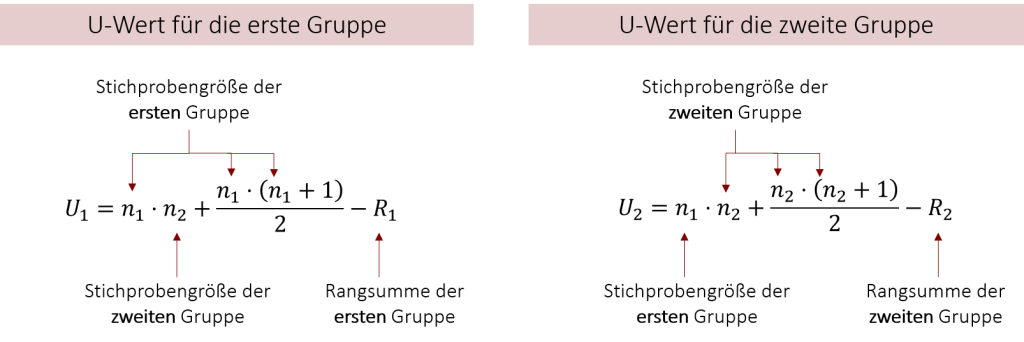
Welches hierbei die erste oder zweite Gruppe ist, können Sie frei entscheiden. In unserem Beispiel ist die erste Gruppe Burgersauce „spicy“ und die zweite Gruppe Burgersauce „sweet“. Daraus ergeben sich folgende U-Werte:

Anschließend wählen Sie den kleineren von beiden U-Werten aus und erhalten dadurch die Prüfgröße U. In unserem Beispiel erhalten wir so einen Wert von U=17,5. Wie bereits beim Rangsummentest nach Wilcoxon kann auch diese Prüfgröße ab einer ausreichenden Stichprobengröße von n>20 (dieser Wert schwankt stark in der Literatur) in eine Normalverteilung approximiert werden. In diesem Fall können wir unsere Teststatistik U mittels einer z-Transformation in einen z-Wert umrechnen.
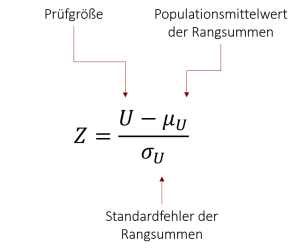
Um nun den entsprechenden z-Wert zu ermitteln, müssen wir, wie auch schon beim Rangsummentest nach Wilcoxon, noch den Mittelwert und Standardfehler der Rangsummen berechnen, da wir diese nicht vorliegen haben. Ihre Formeln lauten wie folgt:
Für unser Burgersaucen-Beispiel erhalten wir durch das Einsetzen so den folgenden z-Wert:
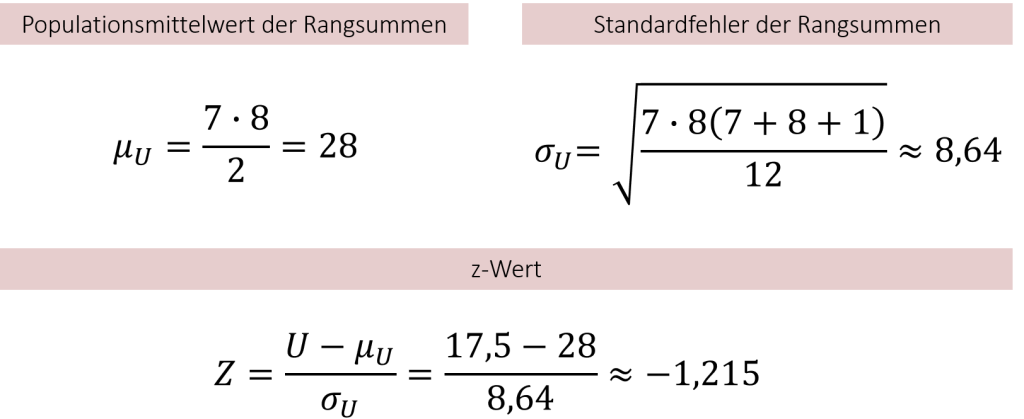
Wie Sie sehen können, entspricht das Ergebnis des Mann-Whitney-U-Test dem des Wilcoxon Rangsummentests und wir erhalten wieder einen z-Wert von -1,215. Aus diesem Grund können Sie frei wählen, welchen der beiden Tests Sie für die Bestimmung von signifikanten Unterschieden verwenden.
Das folgende Video zeigt nochmal die Berechnung des Mann-Whitney-U Test an einem weiteren Beispiel:
13.4 Rangsummentest für Ordinaldaten | Mann-Whitney-U-Test
Doch ist dieser z-Wert nun eine Bestätigung für unsere Hypothese, dass es einen geschmacklichen Unterschied zwischen beiden Burgersaucen gibt? Schauen wir uns hierzu die Interpretation der z-Werte an.
13.5 Interpretation der Rangsummentests
Der eben errechnete z-Wert gibt uns Auskunft darüber, wie wahrscheinlich das Auftreten unserer Messwerte unter Annahme der Nullhypothese ist. Anders ausgedrückt: Wenn die Burgersaucen in ihrem durchschnittlichen Geschmack gleich sind, wie wahrscheinlich ist das Auftreten unseres Unterschieds in den Rangsummen zwischen den zwei Saucen (45,5 vs. 74,5)? Ist das Auftreten unwahrscheinlich genug, können wir unsere Nullhypothese verwerfen und damit unsere Alternativhypothese annehmen. Hierzu vergleichen wir, wie bereits beim z-Test, unseren empirischen z-Wert mit dem kritischen z-Wert, der sich aus unserem Signifikanzniveau ergibt. Graphisch betrachtet versuchen wir damit herauszufinden, ob unser empirischer z-Wert im von uns definierten Ablehnungsbereich liegt.
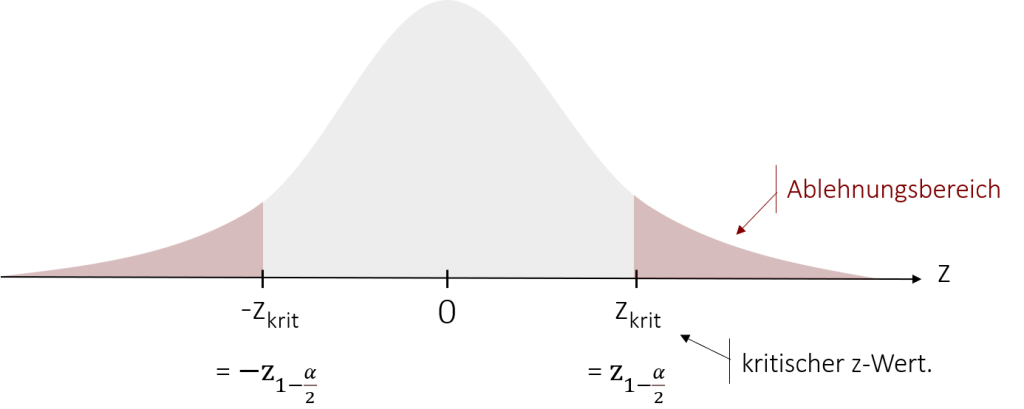
Im Falle unserer ungerichteten Hypothese teilt sich der Ablehnungsbereich auf beide Seiten auf, dessen Grenzen durch den kritischen z-Wert ausgedrückt werden. Welche die kritischen z-Werte zum jeweiligen Signifikanzniveau sind, können Sie in der nachfolgenden Tabelle nachlesen oder alternativ in der Normalverteilungstabellen, z.B. im Anhang, nachschlagen.
| Signifikanzniveau | α-Fehler | 1-α/2 | z1-α/2 |
| 10% | 10% | 95% | 1,65 |
| 5% | 5% | 97,5% | 1,96 |
| 1% | 1% | 99,5% | 2,58 |
In unserem Burgersaucen-Beispiel haben wir vorab ein Signifikanzniveau von 5% gewählt, wodurch unsere kritischen z-Werte bei +/- 1,96 liegen. Diese vergleichen wir nun mit unserem empirischen z-Wert von -1,215. Da der Betrag unseres empirischen z-Werts kleiner ist als der der kritischen z-Werte, können wir unsere Nullhypothese nicht verwerfen und müssen sie beibehalten.
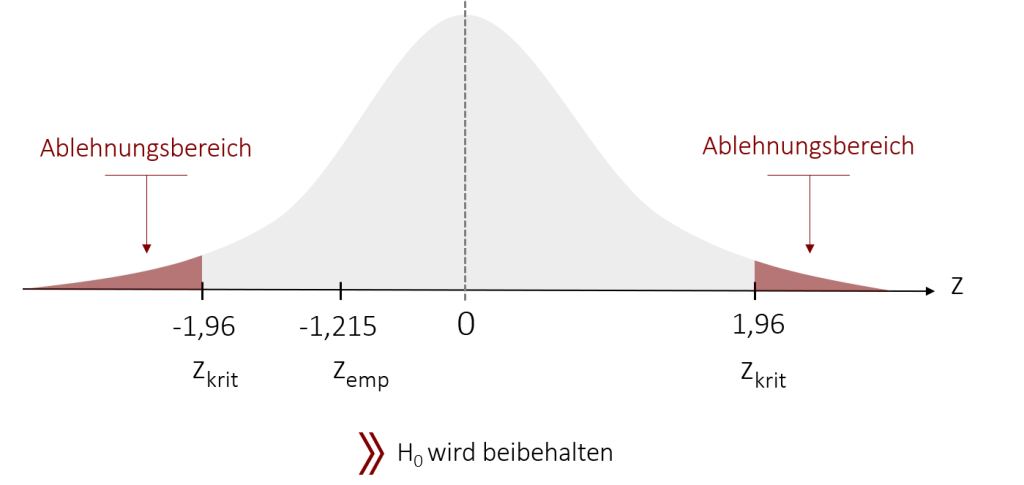
Nochmal zur Erinnerung: Zu Beginn des Kapitels haben wir uns gefragt, ob ein signifikanter Unterschied im Geschmack zwischen der Burgsauce „spicy“ und der Burgersauce „sweet“ besteht. Mittels unserer kleinen Studie konnten wir einen deskriptiven Unterschied in den Rangsummen feststellen, der jedoch nicht statistisch signifikant geworden ist. Somit behalten wir die Nullhypothese bei, dass es keinen Unterschied zwischen den beiden Burgersaucen gibt. Ein Beweis, dass beide Saucen gleich gut schmecken, ist das Testergebnis jedoch ebenfalls nicht. Es bedeutet lediglich, dass unsere Ergebnisse unter Annahme der Nullhypothese nicht unwahrscheinlich genug sind, als dass wir sie hätten ablehnen können.
Das nachfolgende Video veranschaulicht Ihnen die Interpretation noch einmal anhand eines Beispiels aus der FiveProfs-Kette.
13.5 Rangsummentest für Ordinaldaten | Interpretation
13.6 Rangsummentest in SPSS berechnen
Wir haben nun gesehen, dass die Berechnung des Rangsummentest von Hand mit sehr viel Aufwand verbunden ist. Schneller geht es natürlich diesem mit dem Statistikprogramm SPSS zu berechnen. Das Menü zur Berechnung dieses Test ist wieder sehr gut versteckt. Sie müssen zunächst auf „Nicht parametrische Test“ klicken, denn der Rangsummentest verwendet ordinale (also nicht metrisch-skalierte) Daten. Im nächsten Schritt werden Ihnen verschiedene Assistenten angeboten. Da Sie jedoch schon wissen welchen Test Sie durchführen wollen können Sie mit einem Klick auf „Klassische Dialogfelder“ direkt zur Auswahl des „2 unabhängige Stichproben“ wechseln. Hier der ganze Pfad:
Analysieren > Nicht parametrische Test > Klassische Dialogfelder > 2 unabhängige Stichproben
Mit diesem Menü lassen sich verschiedene nicht-parametrische Tests für 2 Testgruppen berechnen. Der Wilcoxon bzw. Mann-Whitney-U Test ist jedoch schon standardmäßig ausgewählt. Sie müssen daher nun die Testvariable und die Gruppierungsvariable definieren. Wie das funktioniert wird im folgenden Video erläutert.
13.6 Rangsummentest für Ordinaldaten in SPSS berechnen
13.7 Übungsfragen
Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!
In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!
13.8 Übungsaufgaben
Übungsaufgabe Berechnung Rangsummentest
Die FIVE PROFS Burger Kette möchte prüfen ihre Kunden schlauer sind als die Kunden der Konkurrenz
| Mc Ronaldo | FIVE PROFS |
| Realschule | Hauptschule |
| Abitur | Realschule |
| Hauptschule | Hauptschule |
| Bachelor | Hauptschule |
| Abitur | Abitur |
| Realschule | Bachelor |
| Hauptschule | Abitur |
| Hauptschule | Hauptschule |
| Hauptschule | Realschule |
| Realschule | Bachelor |
Im folgenden Video wird die Lösung Schritt für Schritt erklärt.
Übungsaufgabe Interpretation Rangsummentest
Im folgenden finden Sie den SPSS Output zu obiger Aufgabe zum Rangsummentest. Interpretieren Sie die Werte. Zu welchem Ergebnis kommen Sie?


