Beispiel

Als Beispiel könnten wir unseren WPStudis Datensatz nutzen und versuchen, das Geschlecht einer Person aus ihrer Schuhgroesse vorhersagen.

Wir nutzen hierzu wieder den WPStudis Datensatz und erstellen ein Subset ohne Missings. Ausserdem schließen wir die Person in Zeile 4 aus (Ausreißer, siehe erstes Regressionsmodell).

data_log <- na.omit(WPStudis[c("F1_Nummer", "F4_Koerpergroesse","F5_Schuhgroesse","F2_Alter", "F3_Geschlecht")])
data_log <- data_log<-data_lm[-4,]

Voraussetzungen

Die gute Nachricht ist, dass logistische Regression weder eine Normalverteilung der Residuen, noch Varianzhomogenität voraussetzt. Auch ein linearer Zusammenhang zwischen AV und UV muss nicht gegeben sein. Dennoch gibt es Voraussetzungen, die erfüllt sein müssen: Die AV muss dichotom sein. Die Beobachtungen müssen unabhängig sein (also kein Messwiederholungsdesign). Drittens sollte es wenig oder keine Korrelation zwischen den UVs geben (Multikollinearität). Hierfür kann man eine Streudiagramm-Matrix verwenden. Da wir in diesem ersten Beispiel nur eine UV haben, ist dies jedoch nicht nötig.

Logistisches Modell erstellen

Die Spezifikation des Modells mit der glm() Funktion ist analog der lm() Funktion (also AV~UV), nur dass wir
zusätzlich das Argument “family=binomial” anhängen.

lm9 <- glm(F3_Geschlecht ~ F5_Schuhgroesse, data=data_log,family=binomial)
summary(lm9)  
## 
## Call:
## glm(formula = F3_Geschlecht ~ F5_Schuhgroesse, family = binomial, 
##     data = data_log)
## 
## Deviance Residuals: 
##      Min        1Q    Median        3Q       Max  
## -2.05356   0.00205   0.00819   0.03280   1.52821  
## 
## Coefficients:
##                 Estimate Std. Error z value Pr(>|z|)  
## (Intercept)      115.722     44.996   2.572   0.0101 *
## F5_Schuhgroesse   -2.774      1.086  -2.555   0.0106 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 84.6304  on 90  degrees of freedom
## Residual deviance:  8.8285  on 89  degrees of freedom
## AIC: 12.829
## 
## Number of Fisher Scoring iterations: 9

Die Regressions-Koeffizienten sind hier schwer zu interpretieren, da sie sich auf Logit (natürlicher
Logarithmus des Wettquotienten) beziehen. Eine Erhöhung der Schuhgroesse um eine Einheit verringert den Logit des Geschlechts (zur Erinnerung “1” war weiblich) um 2,8.

Die Nullabweichung (Null deviance) ist die Abweichung des Modells mit nur dem Intercept-Term. Die Restabweichung ist die Abweichung des Modells mit allen unabhängigen Variablen. Eine geringere Restabweichung zeigt an, dass das Modell besser zu den Daten passt.

AIC (Akaike Information Criterion) ist ein Maß für die relative Qualität eines Modells, das sowohl die Anpassungsgüte als auch die Komplexität des Modells berücksichtigt. Er wird wie folgt berechnet: AIC = 2k – 2ln(L), wobei k die Anzahl der Parameter im Modell und L der maximierte Wert der Likelihood-Funktion ist. Ein niedrigerer AIC-Wert weist auf ein besser passendes Modell hin.

Das Fisher-Scoring, auch bekannt als Fisher-Informationskriterium, ist ein Maß für die relative Qualität eines Modells auf der Grundlage der beobachteten Fisher-Informationen. Es wird berechnet als -2ln(L), wobei L der maximierte Wert der Likelihood-Funktion ist. Niedrigeres Fisher-Scoring deutet auf ein besser passendes Modell hin. Ist ein Maß für die relative Qualität eines statistischen Modells. AIC und BIC werden verwendet, um verschiedene Modelle zu vergleichen. Die AIC- und BIC-Werte sind im Allgemeinen niedriger für Modelle, die besser zu den Daten passen. Für ein einzelnes Modell sind beide jedoch nicht zu interpretieren.

Vorhersagen erstellen

Da die Regressions-Koeffizienten bei einer logistischen Regression nur schwer zu interpretieren sind, ist es spannender, eine Vorhersagefunktion zu bauen. Wir nutzen wieder predict() Funktion. Bei logistischen Regressionsmodellen müssen wir jedoch noch das Argument “type=”response” hinzufügen, um eine Wahrscheinlichkeit zu erhalten (sonst erhalten wir odds ratios)

predict(lm9, data.frame(F5_Schuhgroesse=43), type="response")
##          1 
## 0.02740349

Der Output beantwortet die Frage: Wenn eine Person Schuhgroesse 43 hat, wie hoch ist die Wahrscheinlichkeit, dass es sich um eine Frau handelt? Die Antwort darauf ist 2,7 % (basierend auf diesen Daten). Spielen Sie doch ein wenig mit den Daten, wie ist die Wahrscheinlichkeitsverteilung für Ihre Schuhgroesse?

Der Dichteplot lässt sich auch sehr leicht erstellen. Bei nominalen/dichotomen Verteilungen nutzen wir hierzu die cdplot Funktion (cd steh für conditional densities)

cdplot(F3_Geschlecht ~ F5_Schuhgroesse, data=data_lm)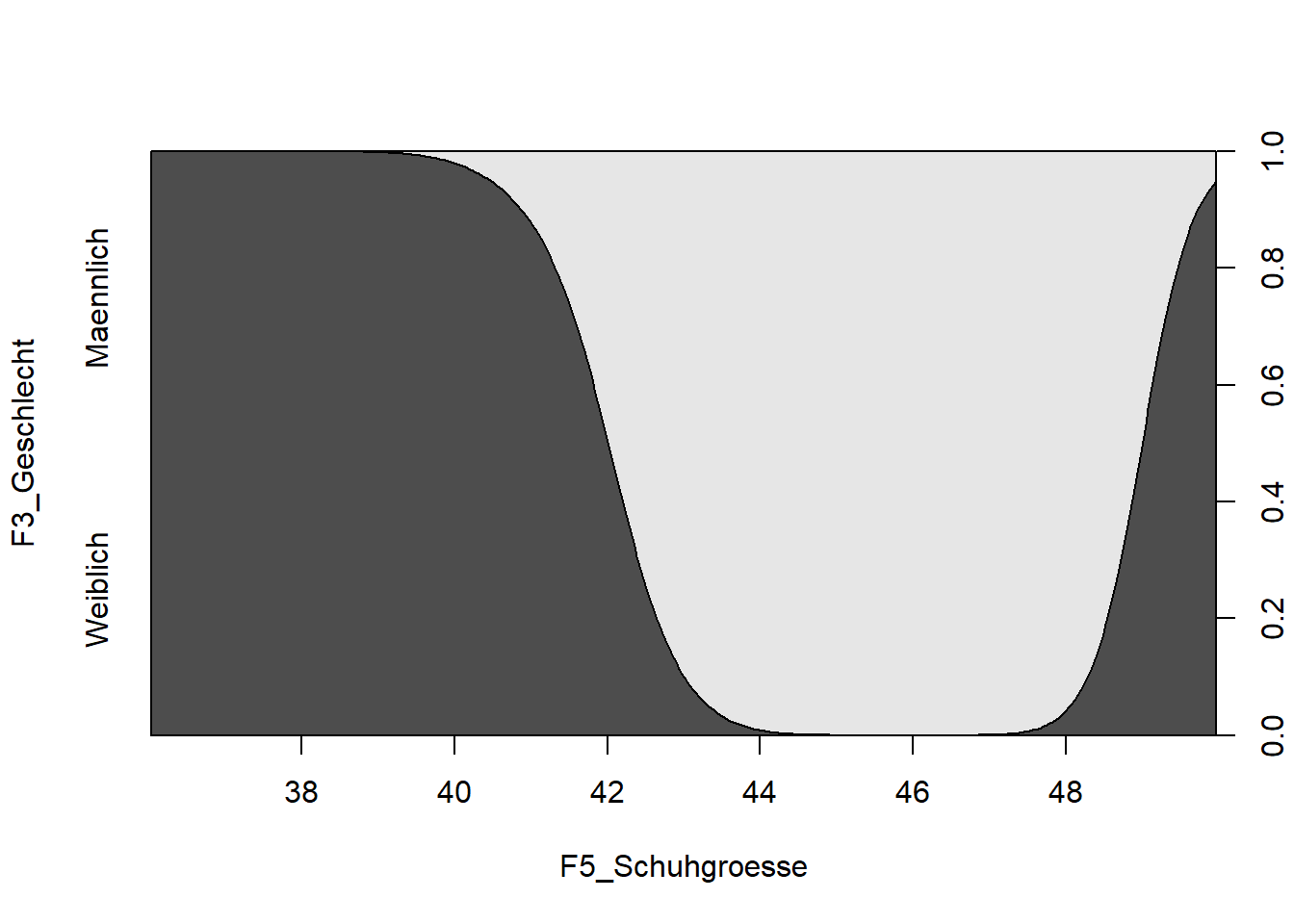

In diesem Video zeige ich, wie das in R funktioniert:

Übung

Learning from Disaster

Der Untergang der Titanic 1912 kostete 1512 Menschen das Leben. Die Plattform Kaggle stellt einen (echten) Datensatz mit 500 echten Personendaten zur Verfügung (https://www.kaggle.com/c/titanic). Neben dem Namen, haben wir Alter, Klasse, Zustiegsort, Kosten des Tickets und einige weitere Variablen. Ausserdem haben wir die Information, ob die Person überlebt hat. Hierfür wollen wir nun ein logistisches Regressionsmodell bauen, welches möglichst gut vorhersagt, ob eine Person überlebt hat oder nicht. Nutzen Sie hierfür: Geschlecht, Alter und Kabinenklasse. Interpretieren Sie das Ergebnis.

titanic <-read.csv(file="titanic.csv")