Statistik mit R & RStudio
31 Multiple Regression mit dichotomen Prädiktoren mit R
Multiple Regression mit dichotomen Prädiktoren
Bei dieser Art von Regression wird eine (oder mehrere) dichotome Variable(n) als binäre Variable (z. B. 0 oder 1) kodiert und zusammen mit den kontinuierlichen Variablen als Prädiktor in das Modell eingegeben.
In R kann die Funktion lm() verwendet werden, um eine multiple Regression mit einem dichotomen Prädiktor durchzuführen. Die dichotome Variable sollte als Faktorvariable eingegeben werden. Anders als SPSS kann R jedoch auch Faktorvariablen mit mehr als zwei Faktorstufen aufnehmen. Diese werden dann in mehrere dichotome Variablen umgewandelt. Dazu mehr in den Beispielen.
Beispiel
Wir wollen der Fragestellung nachgehen, ob wir die Zufriedenheit mit der Partnerschaft aus der allgemeinen Lebenszufriedenheit vorhersagen können. Zusätzlich wollen wir herausfinden, ob die Hinzunahme des Partnerschaftsstatus (hier ein dichotomer Prädiktor mit ja/nein) noch zusätzliche Vorhersagekraft bringt.
´
## Daten vorbereiten
Wir erstellen wieder ein Subset für die Analyse:
data_dicho <- WPStudis[c("F1_Nummer","F19_Partnerschaft","F21_01_Zufriedenheit_Leben","F21_02_Zufriedenheit_Studium","F21_03_Zufriedenheit_Partnerschaft")]Missings ausschliessen:
data_dicho <- na.omit(data_dicho)Vorüberlegungen
Nehmen wir an, wir wollen die Zufriedenheit in der Partnerschaft aus der Zufriedenheit mit dem Leben vorhersagen
Hierfür bauen wir folgendes Model (AV ~ UV).
lm6<- lm(F21_03_Zufriedenheit_Partnerschaft ~ F21_01_Zufriedenheit_Leben , data=data_dicho)
summary(lm6)
##
## Call:
## lm(formula = F21_03_Zufriedenheit_Partnerschaft ~ F21_01_Zufriedenheit_Leben,
## data = data_dicho)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.8298 -0.8298 0.1702 0.7925 2.3032
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.3191 0.5263 4.406 0.0000302
## F21_01_Zufriedenheit_Leben 0.3777 0.1322 2.858 0.00535
##
## (Intercept) ***
## F21_01_Zufriedenheit_Leben **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9463 on 86 degrees of freedom
## Multiple R-squared: 0.08673, Adjusted R-squared: 0.07611
## F-statistic: 8.167 on 1 and 86 DF, p-value: 0.00535Wir sehen, dass die Zufriedenheit mit dem Leben ein signifikanter Prädiktor ist. Die Varianzaufklärung des Modells liegt bei 0,08 oder 8 %.
Unsere Frage ist nun: Bringt der Partnerschaftsstatus (hier ein dichotomer Prädiktor mit ja/nein) noch zusätzliche Vorhersagekraft?
Hinweis: Normalerweise müssten dichotome Variablen erst dummy-codiert werden. R macht dies bei Faktoren aber automatisch. Faktoren, die mehr als zwei Stufen haben, werden automatisch in mehrere Dummies codiert.
Mit der Funktion contrasts() kann überprüft werden, wie R das macht. Schauen wir uns das mal an.
contrasts(WPStudis$F19_Partnerschaft)
## JA
## Nein 0
## JA 1Das sieht sehr einfach aus. Menschen in Partnerschaft bekommen eine 1, Singels eine 0. Schauen wir uns beispielhaft eine Dummy-Codierung für einen Faktor mit mehr als zwei Ausprägungen an.
WPStudis$F6_Sternzeichen
## [1] Krebs Zwilling Jungfrau Fische Jungfrau
## [6] Skorpion Krebs Zwilling Steinbock Zwilling
## [11] Wassermann Loewe Krebs Fische Zwilling
## [16] Schuetze Waage Waage Stier Wassermann
## [21] Fische Zwilling Waage Zwilling Jungfrau
## [26] Waage Loewe Fische Zwilling Jungfrau
## [31] Widder Fische Fische Fische Fische
## [36] Jungfrau Jungfrau Jungfrau Jungfrau Krebs
## [41] Loewe Loewe Loewe Loewe Schuetze
## [46] Schuetze Skorpion Skorpion Stier Stier
## [51] Stier Stier Waage Waage Waage
## [56] Waage Wassermann Wassermann Widder Widder
## [61] Zwilling Zwilling Krebs Wassermann Waage
## [66] Skorpion Loewe Skorpion Wassermann Widder
## [71] Stier Zwilling Jungfrau Widder Schuetze
## [76] Widder Widder Widder Skorpion Zwilling
## [81] Schuetze Waage Wassermann Widder Wassermann
## [86] Stier Loewe Stier Widder Skorpion
## [91] Jungfrau Skorpion Stier
## 12 Levels: Fische Jungfrau Krebs Loewe Schuetze ... Zwilling
contrasts(WPStudis$F6_Sternzeichen)
## Jungfrau Krebs Loewe Schuetze Skorpion Steinbock Stier
## Fische 0 0 0 0 0 0 0
## Jungfrau 1 0 0 0 0 0 0
## Krebs 0 1 0 0 0 0 0
## Loewe 0 0 1 0 0 0 0
## Schuetze 0 0 0 1 0 0 0
## Skorpion 0 0 0 0 1 0 0
## Steinbock 0 0 0 0 0 1 0
## Stier 0 0 0 0 0 0 1
## Waage 0 0 0 0 0 0 0
## Wassermann 0 0 0 0 0 0 0
## Widder 0 0 0 0 0 0 0
## Zwilling 0 0 0 0 0 0 0
## Waage Wassermann Widder Zwilling
## Fische 0 0 0 0
## Jungfrau 0 0 0 0
## Krebs 0 0 0 0
## Loewe 0 0 0 0
## Schuetze 0 0 0 0
## Skorpion 0 0 0 0
## Steinbock 0 0 0 0
## Stier 0 0 0 0
## Waage 1 0 0 0
## Wassermann 0 1 0 0
## Widder 0 0 1 0
## Zwilling 0 0 0 1Hier sieht man, dass R die Variable Sternzeichen mit 12 Faktorstufen in 12 einzelne, dummy-codierte Variablen umwandelt. Hierdurch können wir alle Arten von Faktoren als Prädiktoren in Regressionsmodelle aufnehmen.
Modell erstellen
Nun bauen wir in das Modell den zusätzlichen dichotomen Prädiktor Partnerschaft (ja/nein) ein.
lm7<- lm(F21_03_Zufriedenheit_Partnerschaft ~ F21_01_Zufriedenheit_Leben + F19_Partnerschaft , data=data_dicho)
summary(lm7)
##
## Call:
## lm(formula = F21_03_Zufriedenheit_Partnerschaft ~ F21_01_Zufriedenheit_Leben +
## F19_Partnerschaft, data = data_dicho)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.4621 -0.3310 -0.1383 0.6690 2.0871
##
## Coefficients:
## Estimate Std. Error t value
## (Intercept) 2.2367 0.4159 5.378
## F21_01_Zufriedenheit_Leben 0.2254 0.1065 2.117
## F19_PartnerschaftJA 1.1927 0.1641 7.270
## Pr(>|t|)
## (Intercept) 0.000000651486 ***
## F21_01_Zufriedenheit_Leben 0.0372 *
## F19_PartnerschaftJA 0.000000000162 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.7474 on 85 degrees of freedom
## Multiple R-squared: 0.4369, Adjusted R-squared: 0.4237
## F-statistic: 32.98 on 2 and 85 DF, p-value: 0.0000000000251Wir sehen, auch der Partnerschaftsstatus ist ein signifikanter Prädiktor. Mit beiden Prädiktoren steigt die Varianzaufklärung deutlich auf 0,42 oder 42 %.
Wir sehen also, dass das Modell eine bessere Vorhersage als das Modell ohne den dichotomen Prädiktor ermöglicht. Um zu prüfen, ob der Zuwachs an Vorhersagekraft auch signifikant ist, nutzen wir wieder eine hierarchische Regression.
anova(lm6,lm7)
## Analysis of Variance Table
##
## Model 1: F21_03_Zufriedenheit_Partnerschaft ~ F21_01_Zufriedenheit_Leben
## Model 2: F21_03_Zufriedenheit_Partnerschaft ~ F21_01_Zufriedenheit_Leben +
## F19_Partnerschaft
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 86 77.005
## 2 85 47.479 1 29.526 52.86 0.0000000001624 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Der F-Test wird signifikant. Die Aufnahme des dichotomen Prädiktors erhöht also die Vorhersagequalität des Modells signifikant.
Voraussetzungen prüfen
Auch in diesem Fall müssen wir natürlich noch die Voraussetzungen prüfen. Da dies jedoch dem Vorgehen in den beiden Kapiteln zuvor entspricht, machen wir dies an dieser Stelle nur knapp.
Diagnostik:
par(mfrow=c(2,2)) #4 Graphen pro Seite
plot(lm7)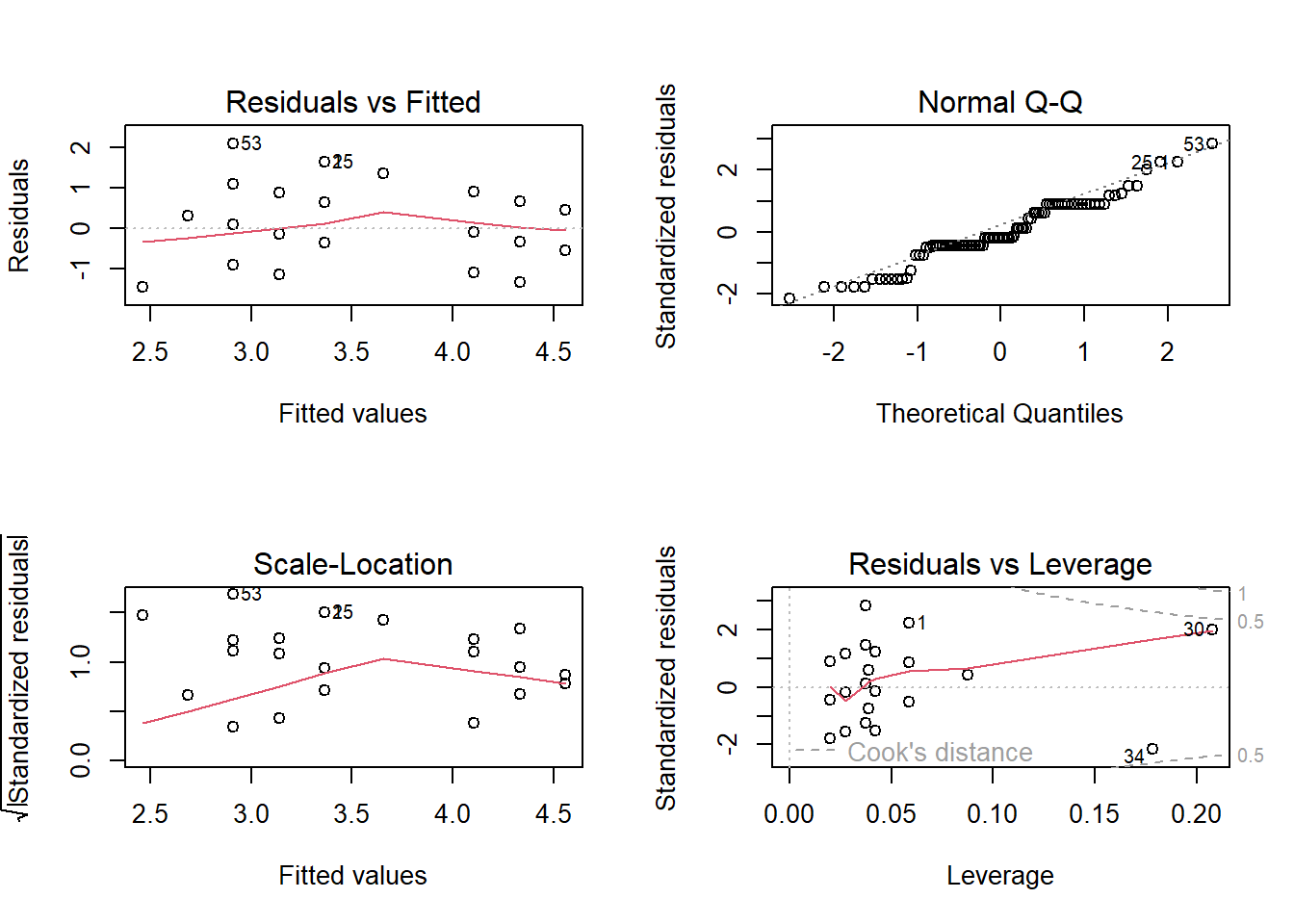
Test auf Multikollinearitaet
vif(lm7)
## F21_01_Zufriedenheit_Leben F19_Partnerschaft
## 1.040259 1.040259In diesem Video zeige ich, wie das in R funktioniert:
Übung
Können wir vorhersagen, wann wie viele Passanten auf der Königstrasse sind?
Daten aus Excel laden
library(readxl)
Passanten <- read_excel("Passanten2019.xlsx")
View(Passanten)Wir wollen aus den Wetterdaten, genauer aus Sonnenscheindauer in Stunden und Regenmenge in Liter, die Besucherfrequenz auf der Königstrasse (Mitte) vorhersagen.
Nun bauen wir das Modell:
lm8 <- lm(Passanten$Koenig_Mitte~Passanten$SONNE_H+Passanten$REGEN)
summary(lm8)
##
## Call:
## lm(formula = Passanten$Koenig_Mitte ~ Passanten$SONNE_H + Passanten$REGEN)
##
## Residuals:
## Min 1Q Median 3Q Max
## -40641 -13888 -5324 5217 108880
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 51893.2 2155.2 24.078 < 0.0000000000000002
## Passanten$SONNE_H -233.4 269.5 -0.866 0.38704
## Passanten$REGEN -964.3 292.5 -3.297 0.00108
##
## (Intercept) ***
## Passanten$SONNE_H
## Passanten$REGEN **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 23230 on 354 degrees of freedom
## Multiple R-squared: 0.02979, Adjusted R-squared: 0.02431
## F-statistic: 5.436 on 2 and 354 DF, p-value: 0.00473Da die Besucherfrequenz zwischen Werktagen und Sonn- und Feiertagen sehr unterschiedlich ist, sollten wir dies als weitere dichotome Prädiktoren aufnehmen. Versuchen Sie die nominalskalierte Variable “Tag” noch in das Modell mit aufzunehmen – was passiert, wie ändert sich das Ergebnis?
Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.


