Zusammenhänge und Vorhersagen
4 Korrelation
4.0 Einführung Korrelation
Bisher kennen Sie zwei Gruppen an Kennwerten: Maße der zentralen Tendenz und Streuungsmaße. In diesem Kapitel lernen Sie nun eine weitere Gruppe an Kennwerten kennen, die sogenannten Korrelationsmaße. Korrelation beschreibt wie Variablen zusammenhängen. Im Folgenden wollen wir uns mit der bivariaten Korrelation, also der Korrelation von genau zwei Variablen beschäftigen.
4.1 Zusammenhang zwischen zwei Variablen
Grundsätzlich kann der Zusammenhang in zwei Dimensionen beschrieben werden: im Hinblick auf die Richtung und auf die Stärke. Zunächst widmen wir uns der Richtung des Zusammenhangs. Mögliche Ausprägungen sind hierbei:
- Positiver Zusammenhang: je höher der Wert einer Variable, desto höher der Wert der anderen Variable. Je niedriger der Werte einer Variable, desto niedriger der Wert der anderen Variable.
- Negativer Zusammenhang: je höher der Wert einer Variable, desto niedriger der Wert der anderen Variable. Je niedriger der Wert der einen Variable, desto höher der Wert der anderen Variable
- Kein Zusammenhang: die Höhe der Werte auf beiden Variablen variieren nicht miteinander. Eine Veränderung der einen Variable hat keinen Einfluss auf die Veränderung der anderen Variable.
Die Stärke des Zusammenhangs drückt aus wie sehr Veränderungen der einen Variable mit Veränderungen der anderen Variable einher gehen. Bei einer sehr starken Korrelation sind die Veränderungen der beiden Variablen stets parallel: z.B. führt eine Verdopplung des Werts einer Variable stets zu einer Verdopplung des Werts der anderen Variable. Bei einer schwächeren Korrelation ist der Einfluss nur unregelmäßig oder geringer. Im Folgenden wollen wir für die Beschreibung der Stärke des Zusammenhangs verschiedene Maße entwickeln, deren Einsatzmöglichkeiten, wie auch bei den bisherigen Kennwerten, vom Skalenniveau der Variablen abhängt.
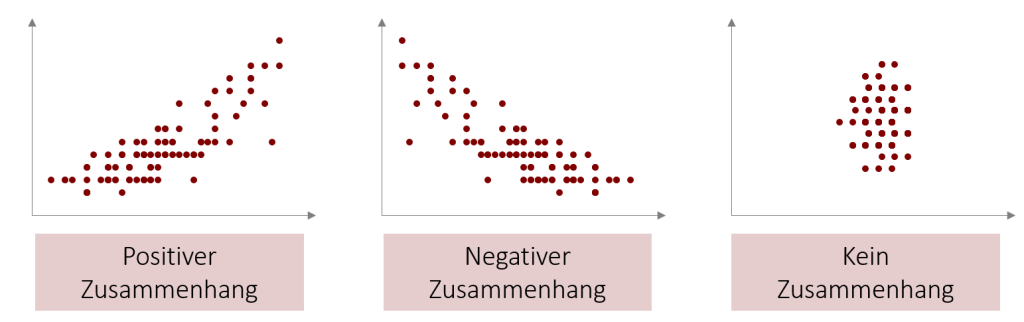
Richtung des Zusammenhangs im Streudiagramm
Alternativ zu Kennwerten lässt sich die bivariate Korrelation auch sehr gut grafisch in einem Streudiagramm darstellen. Bei einem positiven Zusammenhang sollte ein Trend von links unten nach rechts oben erkennbar sein. Bei einer negativen Korrelation ein Trend von links oben nach rechts unten. Falls die Punkte ungeordnet auf dem Streudiagramm verteilt sind und kein Trend ersichtlich ist, so gibt es auch keine Korrelation.
Video 4.0 Korrelation Einführung
4.2 Kreuzprodukt und Kovarianz
Um herauszufinden, ob zwischen zwei Variablen eine Korrelation vorliegt, muss zunächst (als Zwischenschritt) das Kreuzprodukt und die Kovarianz der beiden Variablen berechnet werden. Die Idee dahinter ist relativ einfach: Um zu bestimmen in welcher Weise zwei Variablen zusammenhängen, untersucht man zunächst in wieweit die beiden Variablen kovariieren. In anderen Worten: Wenn es einen Zusammenhang zwischen zwei Variablen gibt, dann sollten die Abweichungen vom Mittelwert auf der einen Variablen mit den Abweichungen vom Mittelwert auf der anderen Variablen einhergehen – in dieselbe oder die entgegengesetzte Richtung. Um hieraus einen Kennwert zu berechnen, werden die Abweichungen jeweils miteinander multipliziert und aufsummiert – dies ist das Kreuzprodukt. Das Kreuzprodukt wird zwangsläufig größer je mehr Werte man betrachtet. Um daher einen Kennwert zu erhalten, der unabhängig von der Anzahl der Werte ist, wird das Kreuzprodukt an der Zahl der Messwerte relativiert (also durch n geteilt). Das Ergebnis ist die Kovarianz.
Die Abkürzung für die Kovarianz ist cov(x,y) wobei x und y die zwei Variablen repräsentieren. Der weitere Aufbau der Formel entspricht der Varianz, die wir in Kapitel 2 besprochen haben, mit dem Unterschied, dass es nun zwei unterschiedliche Mittelwerte gibt.
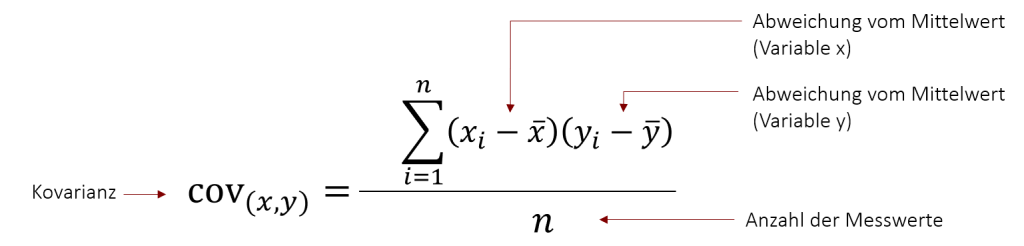
Mit der Kovarianz lässt sich also bestimmen, wie sich die relativen Positionen (Abweichungen vom Mittelwert) von gepaarten Messwerten aus zwei Variablen zueinander verhalten.
Diese Berechnungsweise hilft uns nun die Richtung des Zusammenhangs zu bestimmen:
- Haben Abweichungen vom Mittelwert überwiegend dasselbe Vorzeichen, wird die Kovarianz positiv (Wenn z.B. positive Abweichungen auf der einen Variable meist mit positiven Abweichungen auf der anderen Variable einhergehen)
- Haben Abweichungen vom Mittelwert überwiegend entgegengesetzte Vorzeichen, wird die Kovarianz negativ. (Wenn positive Abweichungen auf der einen Variable meist mit negativen Abweichungen auf der anderen Variable einhergehen)
- Wenn die Abweichungen unsystematisch variieren liegt die Kovarianz nahe Null. (Wenn positive Abweichungen auf der einen Variable mal mit negativen und mal mit positiven Abweichungen auf der anderen Variable einhergehen)
Die Kovarianz hilft uns nun schon einmal die Richtung des Zusammenhangs zwischen zwei Variablen zu interpretieren. Hat die Kovarianz ein positives Vorzeichen, so liegt ein positiver Zusammenhang vor, hat sie ein negatives Vorzeichen, so liegt ein negativer Zusammenhang vor. Aufgrund der Multiplikation der Werte ist jedoch die Größe des Kennwerts nicht so leicht zu interpretieren. Über die Stärke des Zusammengangs kann die Kovarianz also zunächst keine Aussage machen. Hierfür benötigen wir die Korrelationsmaße, denen wir uns nun widmen.
Beispiel Kovarianz
Selbst bei einer überschaubaren Datenmenge ist es oft schwer direkt zu bestimmen, ob es einen Zusammenhang zwischen zwei Variablen gibt. Das folgende Beispiel zeigt die Daten von 5 Person: Die Anzahl der Anzeigen die die Person für unsere neue Burgerkette gesehen hat und die Anzahl Burger, die die Person gekauft hat. Würden Sie sagen, dass hier ein Zusammenhang besteht?
| Person | Anzeigen gesehen | Produkte gekauft |
| 1 | 5 | 8 |
| 2 | 4 | 9 |
| 3 | 8 | 15 |
| 4 | 4 | 10 |
| 5 | 6 | 13 |
Um diese Frage zu klären wollen wir zunächst die das Kreuzprodukt und die Kovarianz bestimmen. Hierzu berechnen wir im ersten Schritt den Mittelwert für beide Variablen (siehe Kapitel 2).
Mittelwerte Anzeigen gesehen: 5,4 und Mittelwert Produkte gekauft:11
Nun können wir das Kreuzprodukt wie folgt berechnen:
(5-5,4) • (8-11) + (4-5,4) • (9-11) + (8-5,4) • (15-11) + (4-5,4) • (10-11) + (6-5,4) • (13-11) = 17
Abschließend relativieren wir das Ergebnis an der Stichprobe und erhalten die Kovarianz:
17/5 = 3,4
Da das Ergebnis mit +3,4 positiv ist wissen wir nun das ein positiver Zusammenhang zwischen den beiden Variablen besteht. Aber was genau bedeutet jetzt die 3,4? Das lässt sich so nicht sagen. Hierfür benötigen wir nun die Korrelationsmaße.
Video 4.3 Korrelation | Kovarianz
4.3 Produkt-Moment-Korrelation
Video 4.4 Korrelation | Pearson Korrelation
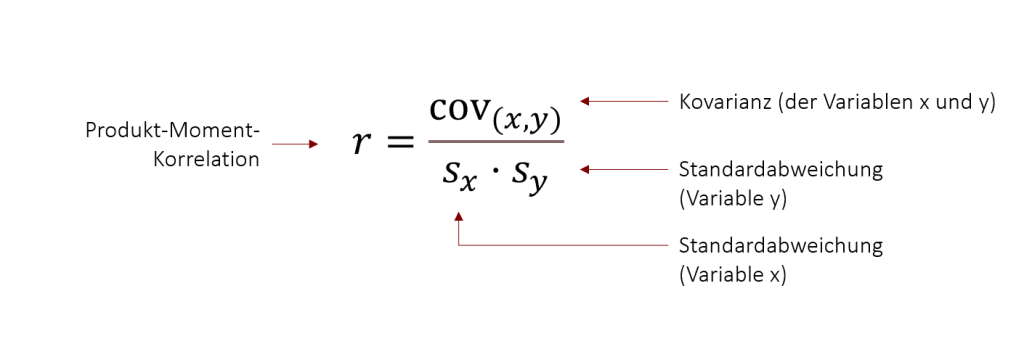
Der Pearson-Korrelationskoeffizient ermöglicht, wie auch die Kovarianz, eine Interpretation der Richtung des Zusammenhangs. Zusätzlich gibt er aber auch eine Information über die Stärke des Zusammenhangs. Denn durch die Standardisierung ist der Korrelationskoeffizient einheitlich interpretierbar (unabhängig davon, welche Variablen betrachtet werden). Durch diese Standardisierung kann der Korrelationskoeffizient r(x,y) nur Werte zwischen –1 und +1 annehmen, wobei
- –1 einen perfekt negativen Zusammenhang zwischen den Variablen aufzeigt
- +1 einen perfekt positiven Zusammenhang zwischen den Variablen aufzeigt
- 0 keinen Zusammenhang zwischen den Variablen aufzeigt
In den ersten beiden Fällen liegen alle Punkte auf einer Graden, was in der Praxis, jedoch nur sehr selten der Fall ist. Aber wie können wir nun Werte zwischen 0 und 1 bzw. zwischen 0 und -1 interpretieren? Hierfür hat Jacob Cohen 1988 eine einheitliche „Sprachregelung“ vorgeschlagen, die bis heute verwendet wird:
- Ab (+/-) r=.10 spricht man von einem schwachen Zusammenhang (schwacher Effekt)
- Ab (+/-) r=.30 spricht man von einem mittleren Zusammenhang (mittlerer Effekt)
- Ab (+/-) r=.50 spricht man von einem starken Zusammenhang (starker Effekt).
Hinweis: Statistiker vermeiden gern unnötige Aufwände, daher wird bei der Angabe des Korrelations-koeffizienten auf die Angabe der „0“ vor dem Komma verzichtet (da der Wert ja nie über 1 liegen kann). Üblicherweise wird auch die englische Schreibweise verwendet also ein Punkt anstatt des Kommas eingesetzt. Die Angabe beginnt also stets mit einem Punkt „.“ wie z.B. r(x,y) = .56 was einem positiven, starken Zusammenhang entspricht.
Beispiel Korrelationskoeffizient
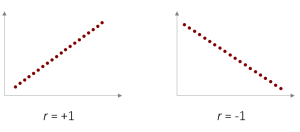
Bei einer perfekten Korrelation (r= +/-1) liegen alle Werte exakt auf einer Linie. Diese lässt sich mit einer Gleichung beschreiben, welche wir näher im nächsten Kapitel „Regression“ betrachten werden.
Eine perfekt lineare Korrelation kommt in der Praxis nur bei technischen Zusammenhängen vor, in den Sozialwissenschaften jedoch sieht die Realität meist eher so aus:
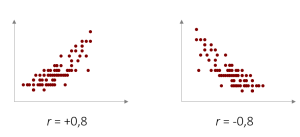
Wir haben mit dem Korrelationskoeffizienten r nun ein standardisiertes Maß mit dem wir beschreiben können, wie nahe die Punkte auf einer Linie liegen und wie stark damit der Zusammenhang ist. In den vorliegenden beiden Fällen sprechen wir nach der Konvention von Cohen von jeweils einem starken Zusammenhang. Also auf der linken Seite von einem starken positiven Zusammenhang und auf der rechten Seite von einem starken negativen Zusammenhang.
Video 4.5 Korrelation | Interpretation
4.4 Rangkorrelation
Die Berechnung des Pearson-Korrelationskoeffizienten setzt voraus, dass beide Variablen metrisch skaliert sind. Hat eine der beiden Variablen oder beide Variablen ordinales Skalenniveau muss anstatt der Pearson Korrelation eine sogenannte Rangkorrelation gerechnet werden. Dabei ist Rangkorrelation der Überbegriff für mehrere Verfahren, die hierbei angewendet werden können. Die in der Praxis gängigen Korrelationskoeffizienten für ordinale Variablen sind Kendall’s Tau (τ) und Spearman’s Rho (rs).Beide Korrelationsmaße berücksichtigen ausschließlich die Ränge, bzw. Rangunterschiede beider Variablenausprägungen. Die Skala reicht jeweils von -1 bis +1 und erlaubt somit eine Interpretation analog Pearson‘s r. Kendalls tau ist systematisch etwas geringer als Spearman‘s Rho und damit das konservativere Maß.
Expertenwissen Rangkorrelation
Beide Rangkorrelationsmaße sind in gängigen Statistik-Programmen (SPSS, R) vorhanden und werden äußert selten von Hand berechnet. Hier finden Sie die entsprechenden Berechnungsverfahren. Falls Sie eines der Verfahren händisch berechnen wollen bietet sich Spearman’s Rho an, da es das deutlich weniger komplexe Verfahren ist.
Spearman’s Rho (rs) wurde entwickelt von Charles Edward Spearman 1904.
Die Formel lautet:
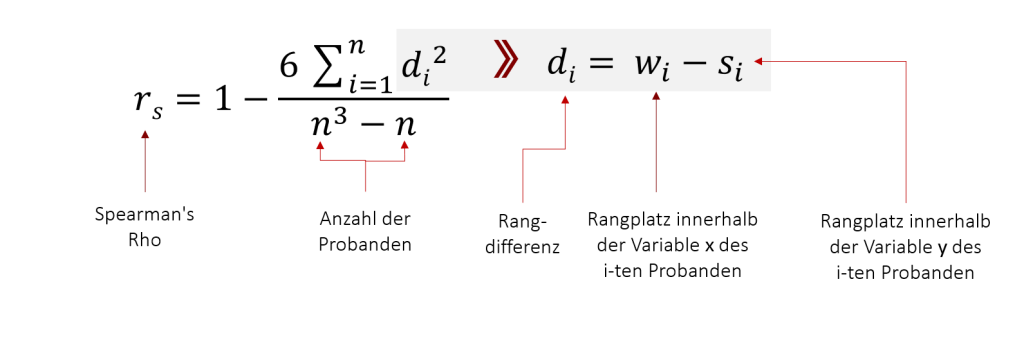
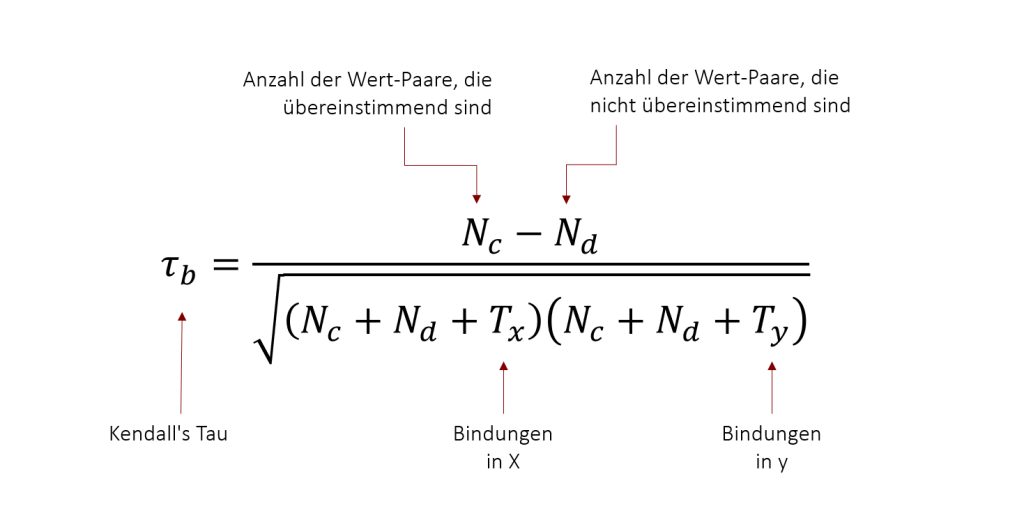
Kendall’s Tau (τ) wurde entwickelt von Maurice Kendall in 1938.
Die Formel lautet:
4.5 Phi Koeffizient
Bei zwei nominalen Variablen kommt ein weiterer Korrelationskoeffizient zum Einsatz: Phi (φ). Allerdings kann dieser nur dann angewendet werden, wenn beide Variablen dichotom sind, d.h. genau zwei Ausprägungen haben. Ein Anwendungsfall wäre also z.B. die Frage, ob es einen Zusammenhang gibt zwischen dem Geschlecht (m/w) und dem Hobby Tennis spielen (ja/nein). Auch beim Phi-Koeffizient reicht die Skala von -1 bis +1 und erlaubt somit eine Interpretation analog Pearson‘s r. Der Phi-Koeffizient ist eng verwandt mit dem Chi-Quadrat Test, den wir später noch kennen lernen werden.
Expertenwissen Phi-Koeffizient
Auch der Phi-Koeffizient ist in gängigen Statistik-Programmen (SPSS, R) vorhanden und wird äußert selten von Hand berechnet. Hier finden Sie die dennoch das entsprechende Berechnungsverfahren.
Die Berechnung des Phi-Koeffizienten basiert auf einer Kreuztabelle mit 4 Feldern und Randsummen.
| b1 | b2 | SUMME | |
| a1 | h11 | h12 | h1⋅ |
| a2 | h21 | h22 | h2⋅ |
| SUMME | h⋅1 | h⋅2 | n |
Hierbei sind a1 und a2 die Ausprägungen der einen Variable (z.B. männlich und weiblich) und b1 und b2 die Ausprägungen der anderen (Tennis ja / Tennis nein). In der Kreuztabelle stehen dann die jeweiligen Häufigkeiten. Hieraus errechnet sich der Phi-Koeffizient wie folgt:
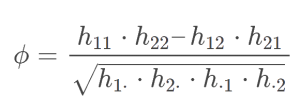
Video 4.1 Korrelation | Korrelationsmaße
4.6 Übersicht Korrelationsmaße
Wir haben nun drei Korrelationsmaße für die drei gängigen Skalenniveaus (metrisch, ordinal, nominal) kennen gelernt. Aufbauend darauf gibt es weitere Korrelationsmaße für spezielle Anwendungen. An dieser Stelle sei noch die Punktbiseriale Korrelation erwähnt, die immer dann verwendet werden kann, wenn eine Variable metrisch ist und die andere dichotom nominal skaliert ist. Zum Beispiel könnte man hiermit der Frage nachgehen ob das Einkommen (metrisch) und das Geschlecht (dichotom nominal) zusammenhängen. Der Vorteil: Die Punktbiseriale Korrelation entspricht mathematisch der Berechnung von Pearson‘s r und kann auch ebenso interpretiert werden. Weitere spezielle Korrelationsmaße wie die Punktbiseriale Rangkorrelation wollen wir an dieser Stelle nicht weiter vertiefen. Die folgende Tabelle soll Ihnen einen Überblick über die Korrelationsmaße geben:
| Intervallskala | Ordinalskala | Dichotome Nominalskala | |
| Intervallskala | Produkt-Moment-Korrelation | Rang-Korrelation (Tau τ/ Rho ρ) | Punkt-biseriale Korrelation |
| Ordinalskala | Rang-Korrelation (Tau τ/ Rho ρ) | Biseriale Rang-Korrelation | |
| Dichotome Nominalskala | Phi-Koeffizient |
Video 4.2 Korrelation | Korrelationsmaße 2
4.7 Voraussetzungen und Grenzen der Korrelation
Wir wollen uns im Folgenden noch mit wichtigen Voraussetzungen und Einschränkungen beschäftigen, welche sowohl die Berechnung als auch die Interpretation von Korrelationsmaßen betrifft.
Grenzen der Linearen Korrelation
Bisher sind wir bei der Produkt-Moment-Korrelation stets davon ausgegangen, dass ein Zusammenhang linear ist (deswegen hätten wir bisher auch ganz korrekt von linearer bivariater Korrelation sprechen müssen). Um besser zu verstehen, was das bedeutet, können wir folgende zwei Streudiagramme betrachten:
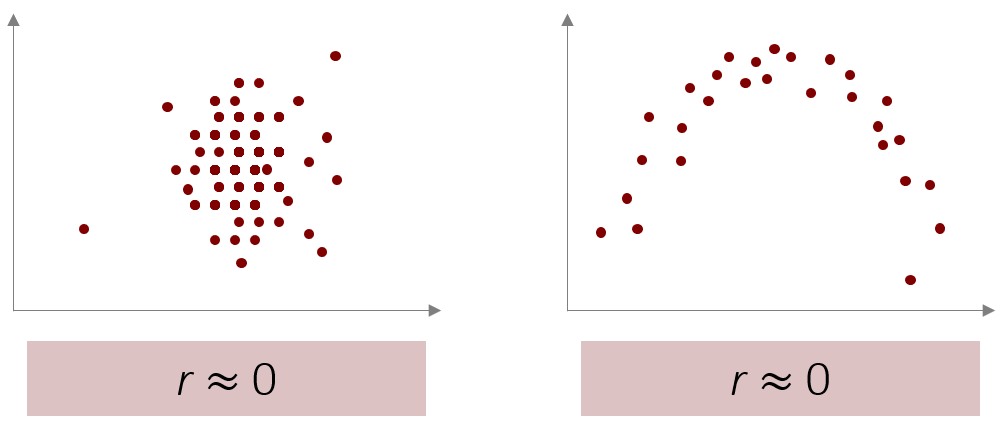
Bei beiden Streudiagrammen liegt der Pearson-Korrelationskoeffizient bei 0 und sagt uns damit, dass es keinen Zusammenhang zwischen den Variablen gibt. Auf der linken Seite scheint dies auch plausibel, jedoch ist rechts deutlich zu erkennen, dass die beiden Variablen zunächst gemeinsam ansteigen, dann jedoch gemeinsam fallen. Da der Pearson-Korrelationskoeffizient nur lineare Zusammenhänge betrachtet (also nur Zusammenhänge die immer in die gleiche Richtung gehen), wird dieser Zusammenhang nicht erkannt. Hierfür gibt es alternative, nicht-lineare, Verfahren die wir hier in Statistik Grundlagen nicht vertiefen können. Ein solcher nicht-linearer Zusammenhang kann jedoch in der Praxis durchaus vorkommen. Ein Beispiel wäre die Arbeitsbelastung und die Arbeitszufriedenheit. Ist die Arbeitsbelastung zu gering sind Angestellte oft gelangweilt und dadurch unzufrieden, ist sie zu hoch kann dies zu Stress und damit auch wieder Unzufriedenheit führen.
Korrelation ist keine Kausalität
Wir haben nun Methoden kennengelernt, mit denen wir zuverlässig feststellen können, ob zwei Variablen zusammenhängen. Dies sagt jedoch nicht aus, dass die eine Variable auch ursächlich für die andere Variable ist. Die Korrelation zweier Variablen bedeutet nicht automatisch, dass es einen kausalen Zusammenhang zwischen beiden Variablen gibt. Dies hat zwei wesentliche Gründe:
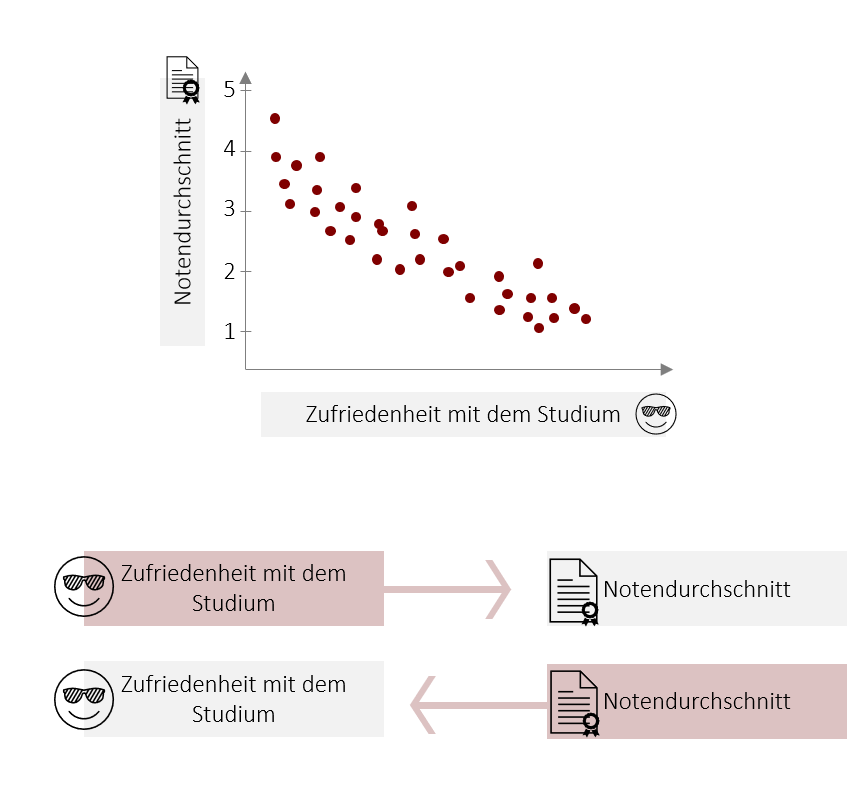
- Eine Korrelation sagt nichts über die Wirkrichtung des Zusammenhangs aus. Grundsätzlich ist ein kausaler Zusammenhang in beide Richtungen denkbar. Wenn Sie z.B. einen Zusammenhang zwischen der Zufriedenheit im Studium (x) und dem Notenschnitt (y) finden. Dann könnte es sein, dass die zufriedenere Studierende wirklich bessere Noten schreiben (Zufriedenheit bewirkt gute Noten), genauso plausibel ist aber auch, dass Studierende, die bessere Noten schreiben, zufriedener sind (gute Noten bewirken Zufriedenheit).
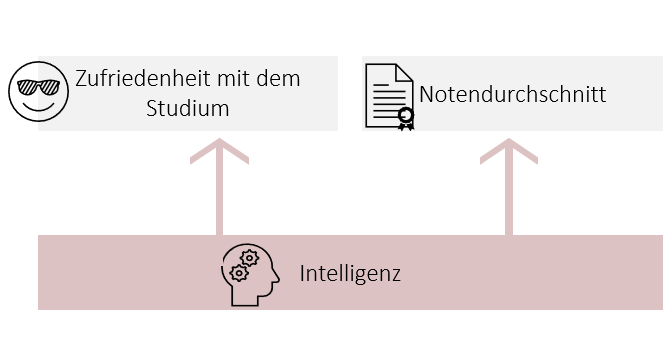
- Zum anderen können beide Variablen von einer dritten Variablen als Ursache abhängen. So könnte z.B. die Intelligenz sowohl die Noten als auch die Zufriedenheit im Studium beeinflussen. In diesem Fall spricht man auch von einer Scheinkorrelation (wenn nur diese dritte Variable für den Zusammenhang verantwortlich ist).
Nur ein entsprechendes Studiendesign (z.B. ein Experiment) ermöglicht die Ableitung von kausalen Zusammenhängen.
Video 4.6 Korrelation | Vorraussetzungen und Grenzen
4.8 Korrelation mit SPSS berechnen
Korrelationskoeffizienten können in SPSS mit wenigen Klicks errechnet werden. Das entsprechende Menü hierzu findet sich unter:
Analysieren > Korrelation > Bivariat
Im folgenden Video besprechen wir, wie die Pearson-Korrelation, sowie die Rangkorrelationskoeffizienten Kendall’s Tau und Spermans Rho, mit SPSS berechnet werden.
Video 4.7 Korrelation | Mit SPSS Korrelationskoeffizienten berechnen
Korrelationen können auch für dichotom nominal skalierte Variablen leicht in SPSS berechnet werden. Im folgenden Video besprechen wir, wie die Punkt-Biseriale Korrelation, sowie der Phi-Koeffizient mit SPSS berechnet werden kann.
Video 4.8 Korrelation | Mit SPSS Korrelation für Nominaldaten berechnen
2.9 Übungsfragen
Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!
In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!
2.10 Übungsaufgaben
Hinweis: Die einzelnen Lösungsschritte werden durch das Bewegen des Schiebereglers sichtbar.
- Franka Miriam Brückler: Geschichte der Mathematik kompakt. Das Wichtigste aus Analysis, Wahrscheinlichkeitstheorie, angewandter Mathematik, Topologie und Mengenlehre. Springer-Verlag, 2017, ISBN 978-3-662-55573-6, S. 116. ↵


