Inferenzstatistik
7 Stichproben
7.0 Population und Grundgesamtheit
Mithilfe der Inferenzstatistik möchte man Aussagen über eine Population, basierend auf einer Stichprobe ableiten. Doch was versteht man eigentlich unter einer Population?
Die Population oder Grundgesamtheit bezeichnet die Menge aller Elemente bzw. Merkmalsträger (Personen, Objekte), über die Aussagen getroffen werden sollen. Sie sollte zu Beginn einer Untersuchung so präzise wie möglich formuliert werden. Geht es zum Beispiel wieder um den Burgerkonsum der Studenten, so muss zunächst klar beschrieben werden, wer als „Student“ zählt. Handelt es sich um alle eingeschriebenen Studenten? Zählen nur staatliche oder auch private Hochschulen? Werden Promovierende mitgezählt? Diese und viele weitere Fragen sollen vor der Untersuchung so eindeutig wie möglich beantwortet werden.
Beispiel Population
Wenn Sie eine Aussage darüber treffen möchten, wie die WhatsApp-Nutzer in Deutschland dazu stehen, dass WhatsApp in Zukunft kostenpflichtig werden soll, so ist die Grundgesamtheit bzw. die Population, auf die Sie sich beziehen alle WhatsApp-Nutzer in Deutschland
Weitere Beispiele für Grundgesamtheiten/ Populationen sind:
- Alle Studierenden einer Hochschule
- Alle Primark-Kunden
- Alle SPD-Wähler
7.1 Stichprobe
Nachdem die Population möglichst exakt bestimmt ist, zieht man im nächsten Schritt eine Stichprobe aus dieser Population. Mit einer Stichprobe bezeichnet man also eine nach einer bestimmten Auswahlmethode gewonnene Teilmenge der Grundgesamtheit. Bevor wir näher auf die Auswahlmethoden eingehen, wollen wir zunächst beschreiben, was eine „gute Stichprobenziehung“ ausmacht. Eine „gute Stichprobe“ ermöglicht eine möglichst genaue Schätzung des interessierten Merkmals für die Population. Die Güte der Schätzung wird dabei von der Kombination zweier Kriterien beeinflusst:
- Stichprobengröße
- Repräsentativität der Stichprobe.
Stichprobengröße
Mithilfe einer Stichprobenziehung möchten wir in der Inferenzstatistik die unbekannten Werte einer Population schätzen (z.B. den Burgerkonsum in ganz Deutschland). Diese Schätzung sollte im Idealfall möglichst genau und verlässlich sein. Ein Faktor, der diese Genauigkeit unter anderem bedingt, ist die Stichprobengröße. Je größer dabei die Stichprobe, desto genauer ist die Schätzung und damit die Ergebnisse.
Beispiel Stichprobengröße
Wir möchten den Mittelwert des jährlichen Burgerkonsums pro Person in Deutschland schätzen. Hierfür befragen wir in einer ersten Studie zufällig gewählte 30 Personen und in einer zweiten Studie zufällig gewählte 3000 Personen zu ihrem Burger-Konsum. Welche Studie wird die genauere Schätzung des Burgerkonsums in Deutschland ergeben? Richtig, die zweite Studie. Durch die größere Stichprobe können exaktere Rückschlüsse über die Population gewonnen werden. Wir werden im Kapitel 8 einen Weg kennen lernen, diese „höhere Sicherheit der Schätzung“ auch exakt in Wahrscheinlichkeiten auszudrücken.
In der Praxis werden unter anderem aus dem Grund der Genauigkeit der Schätzung, aber auch aufgrund der Repräsentativität (darauf kommen wir gleich zu sprechen), der Reduzierung von Abweichungen und der Einhaltung bestimmter Voraussetzungen, möglichst große Stichproben angestrebt. Hierbei haben sich in unterschiedlichen Untersuchungsgebieten verschiedene angestrebte Mindestgrößen bei Stichproben herausgestellt, die allerdings nur als „Daumengrößen“ zu verstehen sind:
| Wissenschaft | n > 30 (teilweise auch kleinere Stichproben) |
| Marktforschung | n > 50 |
| bevölkerungsrepräsentative Studien | n > 1000 |
Repräsentativität einer Stichprobe
Der Rückschluss von der Stichprobe auf die Grundgesamtheit ist nur dann möglich, wenn die Merkmalsträger der Stichprobe, die Merkmalsträger der Grundgesamtheit, in Bezug auf bestimmte Merkmale, hinreichend gut repräsentieren. Einfacher ausgedrückt bedeutet das: Nur wenn die Stichprobe die Grundgesamtheit gut genug abbildet, können wir Befragungsergebnisse der Stichprobe auch auf die Population übertragen und so Aussagen über sie treffen. Das Ziel ist hierbei grundsätzlich, dass die Stichprobe ein verkleinertes Abbild der Population darstellt. Dieses Ziel wird immer angestrebt, aber in der Praxis nie vollumfänglich erreicht. Daher sollte die Repräsentativität nicht als dichotomes Merkmal einer Stichprobe (liegt vor/ liegt nicht vor), sondern eher als Kontinuum verstanden werden. Eine geeignete Stichprobe sollte also die Grundgesamtheit möglichst gut abbilden. Doch woher wissen wir, ob eine Stichprobe die Grundgesamtheit nun hinreichend gut abbildet?
Zunächst einmal muss unsere Stichprobe nicht in jeglicher Hinsicht die Grundgesamtheit abbilden, sondern nur bezüglich derjenigen Merkmale, die für unsere aktuelle Forschungsfrage relevant sind. Damit meint man alle Merkmale, die theoretisch einen Einfluss auf unsere zu untersuchenden Variablen haben können. In der Praxis werden hierfür oft soziodemographische Variablen wie das Alter, Geschlecht, Einkommen etc. genutzt. Jedoch können auch andere, spezifischere Merkmale wie präferierte Marken oder Konsum bestimmter Produkte zu den relevanten Merkmalen zählen, die im Hinblick auf die Repräsentativität der Stichprobe betrachtet werden. Beispielsweise kann eine Stichprobe im Hinblick auf die Geschlechterverteilung repräsentativ für die Population sein, jedoch im Hinblick auf ein anderes Merkmal (z.B. Beruf) weit von der Population abweichen, wenn z.B. nur Studierende befragt wurden.
Bei der Beurteilung der Repräsentativität ergibt sich noch eine weitere Herausforderung. Um zu überprüfen, ob die Merkmale unserer Stichprobe den Merkmalen der Population entsprechen, muss die Verteilung der relevanten Merkmale in der Population bekannt sein (z.B. die Verteilung des Einkommens oder die Häufigkeit von Berufsgruppen in Deutschland). Doch dies ist nur selten der Fall, allein schon aufgrund der Tatsache, dass sich die Population ständig verändert und Erhebungen aller Personen (wie der Zensus) sehr selten sind.
Wie kann man daher sagen, ob eine bestimme Probandenanzahl (z.B. 100 Personen )repräsentativ und damit ausreichend ist? Grundsätzlich kann von der Stichprobengröße alleine noch nicht auf die Repräsentativität rückgeschlossen werden. Hierzu muss man diese Größe immer in Bezug zu den zwei oben genannten Kriterien beurteilen: Die Größe der Population und die Verteilungen der relevanten Merkmalsausprägungen in der Population. Für die Untersuchung eines Unternehmens mit 1000 Beschäftigten könnte eine Stichprobe mit 100 Personen durchaus ausreichend sein. Für eine Studie, die Rückschlüsse auf die gesamte deutsche Population erlauben soll oder für eine Studie die auf ein Merkmal abzielt, das in der Population nur selten vorkommt, wäre die Stichprobe wohl eher nicht ausreichend.
Expertenwissen: Externe Validität
Die Repräsentativität ist eine notwendige Bedingung für die Verallgemeinerbarkeit von Ergebnissen und wird auch externe Validität genannt. Die externe Validität beschäftigt sich mit der Frage, inwieweit die Ergebnisse einer Studie hinsichtlich Merkmalsträgern, Orten, Zeit, etc. übertragbar auf die Population bzw. Allgemeinheit sind. Dementgegen geht es bei der internen Validität um die Frage wie gut das Merkmal, welches gemessen werden soll auch gemessen wird. Also wie gut z.B. die Frage nach dem Burgerkonsum in einem Fragebogen den tatsächlichen Burgerkonsum wiedergibt.
Sind noch Fragen zur Repräsentativität offen geblieben? Das folgende Video veranschaulicht die Thematik noch einmal.
Video 7.1 Stichproben | Population & Repräsentativität
7.2 Methoden der Stichprobenziehung
Wie gehen Sie nun vor, wenn Sie Ihre interessierende Grundgesamtheit klar definiert haben und nun eine Stichprobe aus ihr ziehen möchten? Im Folgenden werden wir die verschiedenen Methoden der Stichprobenziehung kennenlernen.
Zufallsstichprobe
Werden aus einer Population rein zufällig Personen (bzw. Merkmalsträger) gezogen, so spricht man von einer Zufallsstichprobe. Diese Art der Stichprobenziehung bietet viele Vorteile. Ist die Zufallsstichprobe groß genug, so werden automatisch auch alle Merkmale der Population in einem ähnlichen Verhältnis in der Stichprobe auftauchen. Sind beispielsweise in der Population 50% Frauen, so wird eine ausreichend große Zufallsstichprobe auch ca. 50% Frauen beinhalten. Vorrausetzung für eine solche Zufallsstichprobe ist, dass jeder zur Grundgesamtheit gehörende Merkmalsträger dieselbe Auswahlwahrscheinlichkeit aufweist. Dies bedeutet, dass jeder Mensch (oder jeder Merkmalsträger) in der Population, die gleiche Chance hat, in die Stichprobe mit aufgenommen zu werden.
Mögliche Auswahltechniken zur Generierung einer Zufallsstichprobe sind beispielsweise:
| Würfeln / Münzwurf | Bei jedem Merkmalsträger wird gewürfelt (bzw. eine Münze geworfen), ob er ausgewählt wird oder nicht. |
| Direktes Auslosen | Für jeden Merkmalsträger wird ein Los angefertigt, in eine Urne gelegt, gemischt und n Lose gezogen. |
| Indirektes Auslosen | Die Merkmalsträger werden durchnummeriert. Anschließend ermittelt man die auszuwählenden Merkmalsträger für die Stichprobe über Zufallsziffern. |
Expertenwissen: Ziehen mit Zurücklegen und Ziehen ohne Zurücklegen
Grundsätzlich unterscheidet man beim Ziehen von Stichproben zwischen „Ziehen mit Zurücklegen“ und „Ziehen ohne Zurücklegen“. Beim Ziehen mit Zurücklegen kann ein und dasselbe Element (also z.B. ein und dieselbe Person) mehrfach in die Stichprobe gelangen. Beim Ziehen ohne Zurücklegen hingegen kann ein und dasselbe Element nur einmal in die Stichprobe gelangen. Für die Stichprobenziehung in der Sozialforschung wird üblicherweise nur letzteres Verfahren verwendet. Das bedeutet, dass Stichproben jede Person immer nur einmal enthalten. Die Variante „mit Zurücklegen“ wird später für die Stichprobenkennwertverteilung und für das Bootstrapping als theoretisches Konzept jedoch noch wichtig sein.
Zufallsstichproben lassen sich in drei Unterkategorien untergliedern: die einfache Zufallsstichprobe, die Schichtenstichprobe, sowie die Klumpenstichprobe.
Einfache Zufallsstichprobe
Einfache Zufallsstichproben sind Zufallsstichproben, wie sie eben bereits beschrieben wurden. Jeder Merkmalsträger hat hierbei dieselbe Chance, in die Stichprobe mit aufgenommen zu werden. Der Begriff „einfache Zufallsstichprobe“ ist hierbei jedoch irreführend. In der Praxis ist diese Form der Stichprobenziehung oft nur schwer umzusetzen. Um eine einfache Zufallsstichprobe zu erheben, benötigt man ein vollständiges Verzeichnis aller Merkmalsträger, aus denen man im nächsten Schritt mithilfe einer Auswahltechnik per Zufall, eine Stichprobe von Merkmalsträgern zieht. Dieses vollständige Verzeichnis aller Merkmalsträger ist in der Realität nur selten gegeben, zumal sich die Grundgesamtheit ständig verändert.
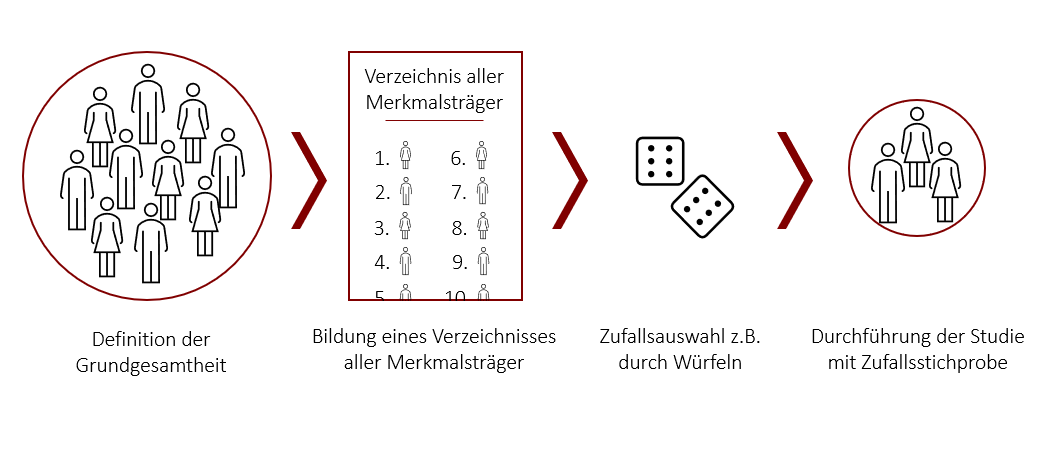
Ein weiteres Problem ist, dass Stichproben die zufällig gezogen wurden, in ihrer Zusammensetzung mehr oder weniger stark von der Zusammensetzung der Grundgesamtheit abweichen. So können wir eine Zufallsstichprobe ziehen, die zufällig nur Frauen oder überwiegend Frauen beinhaltet, obwohl das Merkmal „Frauen“ in der Population nur mit 50% vorkommt. Über viele Stichproben mittelt sich das zwar aus, aber meistens ziehen wir ja nur eine Stichprobe. Ein möglicher Lösungsansatz ist daher die Stichprobengröße zu erhöhen, sodass die Chance auf ein möglichst repräsentatives Verhältnis der Geschlechterverteilung (oder anderer Merkmalsverteilungen) steigt. Eine weitere Möglichkeit ist die geschichtete Zufallsstichprobe, die wir im Folgenden besprechen.
Video 7.2 Stichproben | Zufallsstichprobe
Schichtenstichprobe (Geschichtete Zufallsstichprobe)
Bei einer Schichtenstichprobe wird die Grundgesamtheit zunächst in Untergruppen – sogenannte Schichten – zerlegt. Unterteilt wird hierbei nach relevanten Merkmalsausprägungen, die einen Einfluss auf die interessierenden Variablen einer Studie haben. Die Schichtung erfolgt also nach Merkmalen, die für das Untersuchungsanliegen relevant sind. Beispiele für Schichtungsmerkmale könnten soziodemographische Variablen wie Alter oder Wohnort, aber auch Konsumgewohnheiten oder andere Merkmale sein. Anschließend wird aus jeder Schicht eine Zufallsstichprobe gezogen. Die folgende Grafik zeigt eine Schichtung für ein Merkmal mit drei Ausprägungen. Hierfür könnten z.B. Schulabschlüsse (Hauptschule, Realschule, Abitur) herangezogen werden. Genauso könnte auch ein intervallskaliertes Merkmal (z.B. das Alter) in drei Gruppen eingeteilt werden (z.B. Junge Menschen unter 30, 31 bis 60-Jährige und Personen über 60).
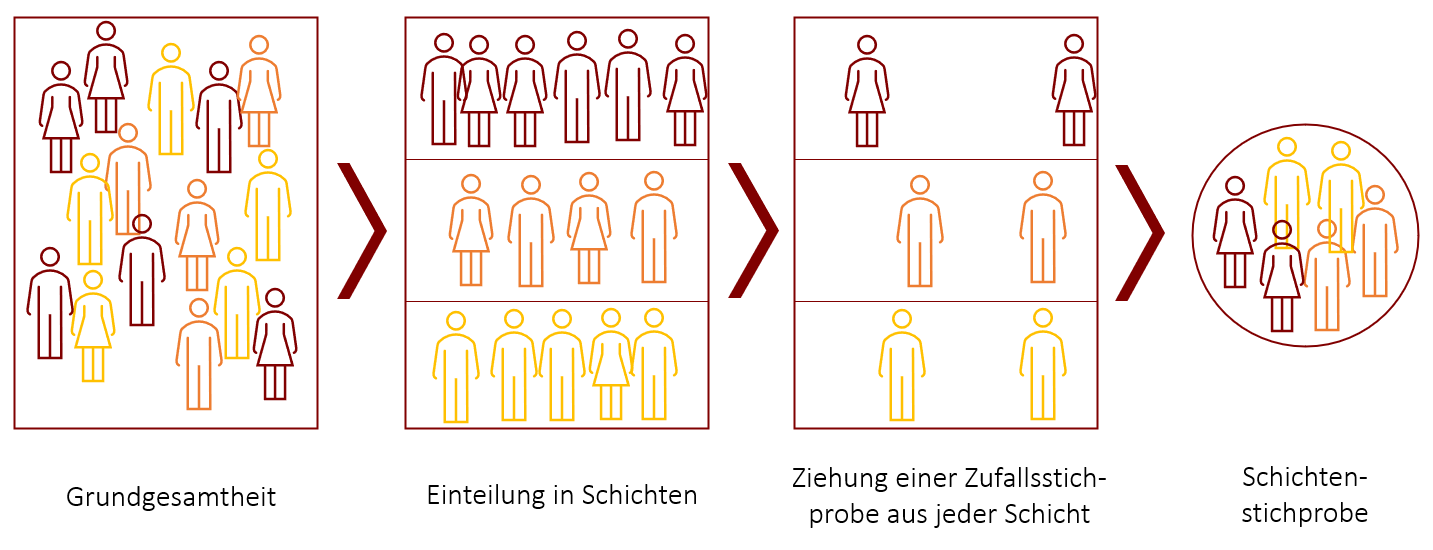
Die Zerlegung der Grundgesamtheit in Schichten kann man auch mehrmals ausführen. Man spricht hierbei von einer mehrstufigen Schichtenstichprobe. Hierbei werden bereits gebildete Schichten, nochmals nach relevanten Merkmalsausprägungen in Untergruppen zerlegt. Man erhält so differenziertere Schichtenkombinationen, aus denen man im letzten Schritt wieder Zufallsstichproben zieht. Hierbei sollten möglichst die Merkmale ausgewählt werden, die für das Untersuchungsanliegen relevant sind. Eine Schichtung nach „Haarfarbe“ würde z.B. für die meisten Untersuchungen wohl keinen Zugewinn an Repräsentativität bedeuten.
Zudem unterscheidet man zwischen einer proportionalen und einer disproportionalen Schichtung. Eine proportional geschichtete Stichprobe erhält man, wenn der Anteil einer Schicht an der Gesamtstichprobe gleich dem Anteil dieser Schicht an der Grundgesamtheit ist. Wenn dies nicht der Fall ist, spricht man von einer disproportional geschichteten Stichprobe. Sie eignet sich beispielsweise für den Fall, wenn eine Schicht so klein ist, dass Sie bei einer proportionalen Schichtung kaum belastbare Ergebnisse liefern würde. Dies bietet daher die Chance auch Merkmale die in der Population sehr selten auftreten, gezielt zu untersuchen. In diesem Fall sollte man jedoch die Kennwerte (wie beispielsweise den Mittelwert) bei der Berechnung gewichten, um die falschen Proportionen der Stichprobe wieder auszugleichen.
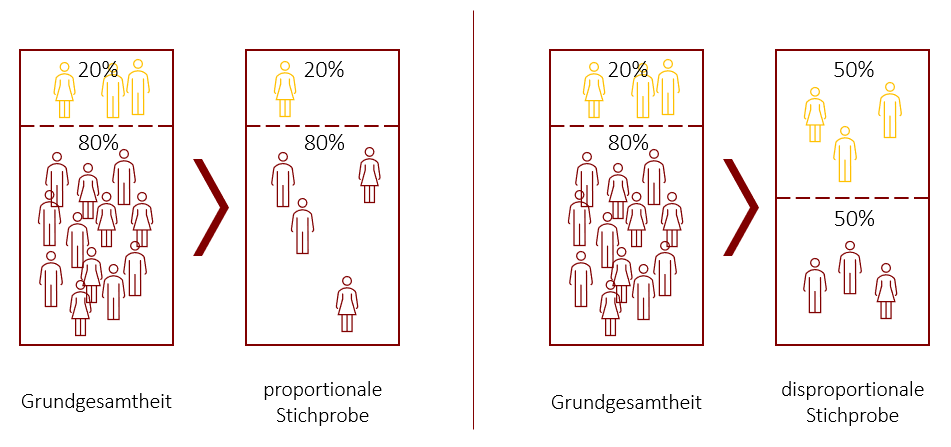
Der Vorteil von Schichtenstichproben ist, dass eine Schichtung die auftretende Zufalls-Varianz reduziert und somit die Genauigkeit der Schätzung bei gleichem Stichprobenumfang erhöht. Jedoch müssen für eine Schichtung im Vorhinein einige Daten über die Population bekannt sein. Insbesondere muss entschieden werden, welche die relevanten Merkmale einer Studie sind. Zudem muss die Verteilung des Schichtungsmerkmals in der Population bekannt sein. Ist dies nicht der Fall, kann keine proportionale Schichtenstichprobe gezogen werden.
Beispiel einer proportionalen Schichtenstichprobe
Wir möchten den Konsum von veganem Eis in Deutschland untersuchen. Hierzu könnte man die Population sehr gut nach ihren Essengewohnheiten schichten. So entstehen in unserer Untersuchung mehrere Schichten: „kein Verzicht auf tierische Produkte“, „Vegetarisch“ und „Vegan“. Aus jeder dieser Schicht können wir nun eine Zufallsstichprobe nehmen. Um die Proportionalität zu gewährleisten muss jedoch die Verteilung des Merkmals bekannt sein. Nehmen wir im Folgenden an, dass bekannt ist, dass in Deutschland 8% vegetarisch leben und rund 1% vegan. Wenn wir nun eine Stichprobe von 300 Menschen befragen möchten, so ziehen wir per Zufall 3 Probanden aus der Schicht „Vegan“, 24 Probanden aus der Schicht „Vegetarisch“ und 273 Probanden, die auf tierische Produkte nicht verzichten.
Noch ein Beispiel gefällig? Das folgende Video verdeutlicht die Schichtenstichprobe anhand von vegetarischen Burgern.
Video 7.3 Stichproben | Schichtenstichprobe
Klumpenstichprobe
Bei der Klumpenstichprobe wird die Grundgesamtheit zunächst hinsichtlich eines Merkmals in natürliche Klumpen eingeteilt (beispielsweise Klassen in einer Schule). Anders als bei Schichten sollten die Klumpen hierbei untereinander möglichst homogen sein. Das bedeutet, dass idealerweise jeder Klumpen ein verkleinertes Abbild der Population ist und sich daher alle Klumpen stark ähneln. Aus diesen Klumpen werden per Zufallsauswahl einige ausgewählt, in denen im nächsten Schritt eine Vollerhebung durchgeführt wird. Das heißt sämtliche Merkmalsträger der ausgewählten Klumpen werden in die Stichprobe mit aufgenommen und befragt.
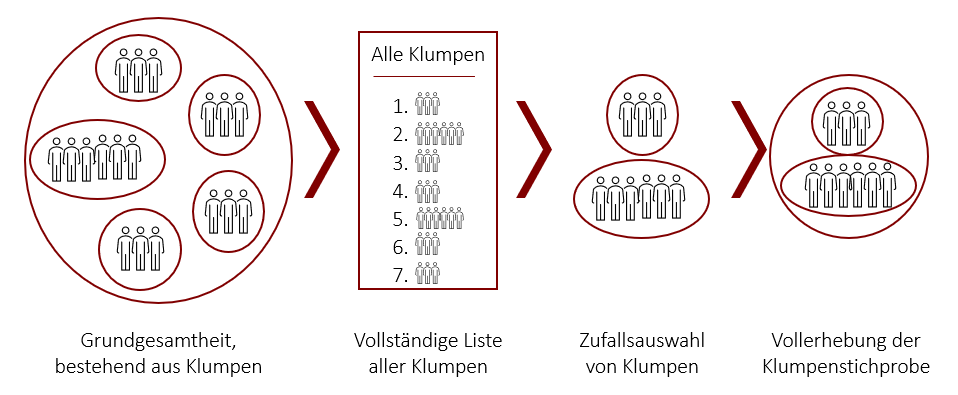
Für diese Vorgehensweise gelten folgende Voraussetzungen:
- Die gesamte Population ist in Klumpen eingeteilt, welche bekannt sind.
- Jeder Merkmalsträger muss eindeutig einem Klumpen zugeordnet sein.
- Jeder Klumpen sollte möglichst gleichermaßen gut die Population repräsentieren.
Ein wesentlicher Vorteil der Klumpenstichprobe ist, dass nicht alle Merkmalsträger bekannt sein müssen, um sie durchführen zu können. Dadurch vereinfachen wir nicht nur die Auswahl, sondern reduzieren auch unsere Erhebungskosten. Jedoch können auch Probleme durch diese Methode auftreten. Beispielsweise können Klumpen teilweise zu groß sein, um alle Merkmalsträger erfassen zu können (beispielsweise bei Wahlkreisen) oder die Klumpen sind untereinander nicht homogen, sodass dadurch die Ergebnisse verzerrt werden. Dies zeigen die folgenden Beispiele nochmal im Detail.
Beispiele Klumpenstichproben
Stimmbezirke als Klumpen
Möchte man eine Untersuchung der Wahlberechtigten der Stadt Leipzig durchführen, so könnte man aus den 329 Stimmbezirken der Stadt Leipzig eine Zufallsstichprobe von z.B. 10 Stimmbezirken ziehen. In jedem Stimmbezirk könnte man nun alle Wahlberechtigten befragen. Der Nachteil ist hierbei jedoch, dass sich die Stimmbezirke hinsichtlich bestimmter Merkmale unterscheiden könnten. Falls daher z.B. sozio-ökonomische Merkmale in der Studie von Interesse sind, so wäre es durchaus relevant, dass in bestimmten Stimmbezirken eher wohlhabende Personen wohnen, während in anderen eher arme Personen wohnen.
Schulen als Klumpen
Eine vollständige Liste von Schulklassen existiert selbst innerhalb eines Bundeslandes oft nicht. Eine Möglichkeit trotzdem Zufallsstichproben von Schulklassen zu ziehen besteht darin, aus der verfügbaren Liste der Schulen zufällig einige Schulen auszuwählen und innerhalb jeder Schule jede Schulklasse in die Stichprobe aufzunehmen. Auch hier hängt es vom Untersuchungsgegenstand ab, ob Schulen wirklich als homogene Klumpen angenommen werden können.
Das folgende Video veranschaulicht die Klumpenstichproben anhand von Filialen der Burgerkette FiveProfs.
Video 7.4 Stichproben | Klumpenstichprobe
Vergleich: Klumpen- und Schichtenstichprobe
Klumpen- und Schichtenstichproben ähneln sich auf den ersten Blick. Dennoch besitzen sie einige Unterschiede, an denen die beiden Methoden deutlich von einander abgegrenzt werden können. In der folgenden Tabelle werden die wesentlichen Unterschiede zusammenfassend dargestellt.
| Klumpenstichprobe („cluster sampling“) | Schichtenstichprobe („stratified sampling“) |
| Jedes Element der Grundgesamtheit gehört zu genau einem Klumpen. | Jedes Element der Grundgesamtheit gehört zu genau einer Schicht. |
| In der Regel entsprechen die Klumpen „natürlichen“ Gruppierungen. | In der Regel entsprechen die Schichten willkürlich gewählten Merkmalen. |
| Es wird eine einfache Zufallsstichprobe aus der Menge der Klumpen gezogen. | Alle Schichten werden berücksichtigt. |
| Innerhalb eines ausgewählten Klumpens gelangen alle Elemente in die Stichprobe. | Aus jeder Schicht wird jeweils eine Zufallsstichprobe gezogen. |
Mehrstufige Stichproben
Mehrstufige Stichproben bestehen aus einer Kombination der eben genannten Methoden, wie Schichten- oder Klumpenstichproben. Dadurch lassen sich angestrebte Zufallsstichproben ökonomischer bzw. einfacher realisieren. Im einfachsten Fall werden beispielsweise per Zufallsauswahl zunächst Klumpen ausgewählt, woraufhin aus jedem Klumpen zufällig eine Stichprobe gezogen wird. Dies wäre eine Kombination aus Klumpenstichprobe und einfacher Zufallsstichprobe. Man kann jedoch auch weitere Stufen dazwischenschalten oder andere Methoden kombinieren.
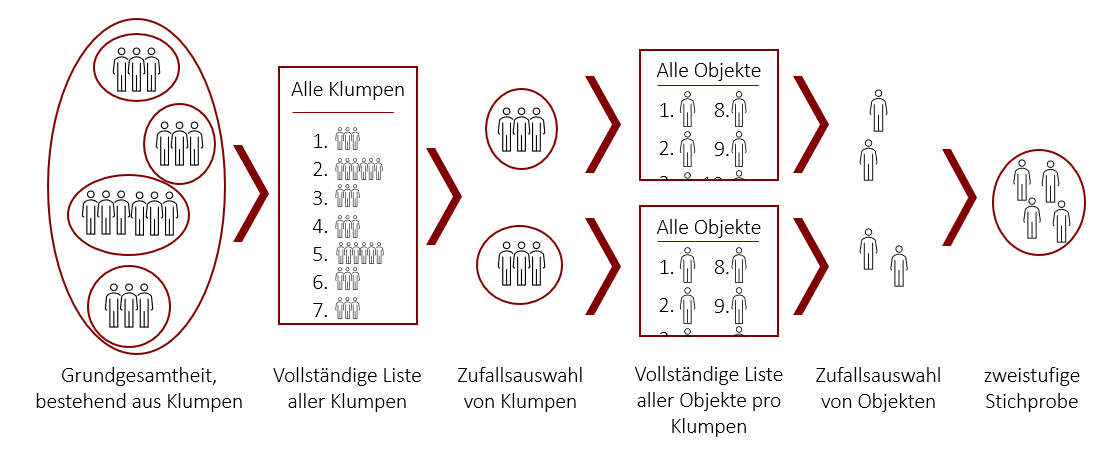
Beispiel Mehrstufige Stichprobe
Es soll eine Befragung zu Arbeitsbedingungen in Krankenhäusern in Deutschland durchgeführt werden.
Hierfür wird zuerst eine vollständige Liste mit allen Krankenhäusern erstellt (Krankenhäuser als Klumpen). Danach wird eine zufällige Auswahl von den zu untersuchenden Krankenhäusern getroffen (Klumpenstichprobe). Im nächsten Schritt werden die Anteile der Mitarbeiter der jeweiligen Berufsgruppen der Kliniken ermittelt um dadurch eine proportionale Schichtung zu erreichen (Berufsgruppen als Schichten). Nun werden jeweils in allen gewählten Kliniken in den Berufsgruppen proportional zu ihrem Auftreten Zufallsstichproben gezogen. Beispielsweise könnten 5 Kliniken als Klumpen ausgewählt werden, in denen dann jeweils 100 Mitarbeiter befragt werden. Wenn in einer Klinik z.B. 30% Krankenpfleger angestellt sind so werden hierbei 30 zufällig ausgewählte Krankenpfleger befragt.
Als weiteres Beispiel wird im folgenden Video eine Kombination aus einer Klumpen- und einer Schichtenstichprobe gezeigt.
Video 7.5 Stichproben | Mehrstufige Stichproben
7.3 Die Grenzen von Stichproben
Streng genommen ist eine Zufallsstichprobe das einzige Verfahren, das uneingeschränkte Schlussfolgerungen von der Stichprobe auf die Grundgesamtheit zulässt. Diese setzt voraus, dass jeder Merkmalsträger die gleiche Chance hat in die Stichprobe mit aufgenommen zu werden. In der Praxis ist dies jedoch sehr schwer umzusetzen. Man stelle sich vor, dass wir auf die deutschen Autofahrer verallgemeinern möchten. In diesem Fall müssten wir sicherstellen, dass jeder Autofahrer in Deutschland, ob er nun will oder nicht, in unsere Stichprobe fließt und somit an der Studie teilnimmt. Allein schon aufgrund der Datenschutzbestimmungen wäre dies bei solch großen Grundgesamtheiten schwer vorstellbar. Aus diesem Grund werden in der Marktforschung aber auch in der wissenschaftlichen Forschung nur selten Zufallsstichproben gezogen. So haben nur ca. 5% aller veröffentlichten, empirischen Studien in der Psychologie eine Zufallsstichprobe als Grundlage[1]. Die überwiegende Mehrheit arbeitet stattdessen mit sogenannten Gelegenheitsstichproben (z.B. über Aushänge rekrutierte Studierende einer Hochschule). Auch in der angewandten Forschung werden häufig anfallende, theoretische oder Quotenstichproben verwendet, bei denen die Merkmalsträger nicht nach Zufall sondern nach Verfügbarkeit rekrutiert werden. Als Konsequenz verbietet sich bei solchen Erhebungen streng genommen der (wahrscheinlichkeitstheoretisch begründete) Rückschluss auf nicht an der Untersuchung beteiligte Personen. Da es jedoch oft ganz praktisch oder auch ökonomisch nicht anders möglich ist, sollte bei solchen Studien zumindest auf die Einschränkungen bei der Verallgemeinerung der Ergebnisse hingewiesen werden.
7.4 Stichproben mit SPSS ziehen
Liegt ein Verzeichnis der Population in digitaler Form vor, so kann SPSS auch dazu genutzt werden eine echte Zufalls-Stichprobe zu ziehen. Liegt zum Beispiel eine Liste aller Mitarbeiter einer Firma vor, so kann mit SPSS zufällig eine Stichprobe von X Mitarbeitern ausgewählt werden, die im Folgenden dann beispielsweise eine Befragung erhält. Hierzu gehen Sie in folgendes Menü:
Daten > Fälle Auswählen > Zufallsstichprobe.
Hier können Sie Auswählen ob ein gewisser Prozentsatz (z.B. 5% der Fälle) ausgewählt werden soll, oder ob Sie eine feste Anzahl an Fällen (meist Personen) in der Stichprobe haben möchten. Neben der Zufallsziehung mit SPSS werden im folgenden Video auch alternative Methoden der Zufallsziehung gezeigt.
Video 7.6 Stichproben mit SPSS ziehen
7.5 Übungsfragen
Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!
In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!
- Henrich, J.; Heine, S.J., & Norenzayan, A. (2010). The weirdest people in the world? Behavioral and Brain Sciences, 33(2-3), 61-83. doi: 10.1017/S0140525X0999152X ↵



