Statistik mit R & RStudio
28 ANCOVA Kovarianzanalyse mit R
ANCOVA Kovarianzanalyse
Die Kovarianzanalyse (ANCOVA) ist ein statistisches Verfahren, mit dem die Beziehung zwischen einer kontinuierlichen abhängigen Variablen und einer oder mehreren kategorialen unabhängigen Variablen analysiert wird, während gleichzeitig für die Auswirkungen einer oder mehrerer kontinuierlicher Kovariaten kontrolliert wird. Die allgemeine Idee hinter der ANCOVA besteht darin, die Variation in der abhängigen Variable, die durch die Kovariablen erklärt wird, zu bereinigen, so dass die verbleibende Variation den Auswirkungen der unabhängigen Variablen zugeschrieben werden kann.
ANCOVA kann in R mit der Funktion lm() durchgeführt werden, also dem generellen linearen Modell. Die grundlegende Syntax für die Verwendung von lm() zur Durchführung einer ANCOVA lautet wie folgt:
ANCOVA <- lm(abhängige_Variable ~ unabhängige_Variable + Kovariate, Daten = data_frame)
Hier wird die abhängige Variable auf der linken Seite der Formel angegeben, und die unabhängige Variable und Kovariate(n) werden auf der rechten Seite der Formel angegeben, getrennt durch ein + Symbol.
Beispiel
Wir nutzen Datensatz mtcars (in R Hinterlegt). Wir wollen der Frage nachgehen, ob Autos mit Automatikgetriebe (am) mehr Benzin verbrauchen (mpg), als solche mit Schaltgetriebe? Beachten Sie, dass der Verbrauch der Fahrzeuge hier in Miles per Gallon (mpg) angegeben ist und hier ein kleinerer Wert einen größeren Verbrauch angibt (Das Fahrzeug schafft weniger Meilen mit einer Galone Benzin).
Daten laden
Da die Daten in r hinterlegt sind, müssen wir die Daten nicht laden, sondern können direkt darauf zugreifen. Schauen wir uns die Daten zunächst einmal an.
head(mtcars)
## mpg cyl disp hp drat wt qsec vs am gear
## Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4
## Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4
## Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4
## Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3
## Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3
## Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3
## carb
## Mazda RX4 4
## Mazda RX4 Wag 4
## Datsun 710 1
## Hornet 4 Drive 1
## Hornet Sportabout 2
## Valiant 1Verwenden Sie die Hilfefunktion zu diesem Datensatz mit ?mtcars, um diesen näher zu verstehen. Das Wichtigste: Bei der Variable am bedeutet 0 Automatikgetriebe und 1 Handschaltung.
Deskriptive Analyse
Betrachten wir die Daten zunächst mit Hilfe eines Boxplots.
boxplot(mtcars$mpg~mtcars$am)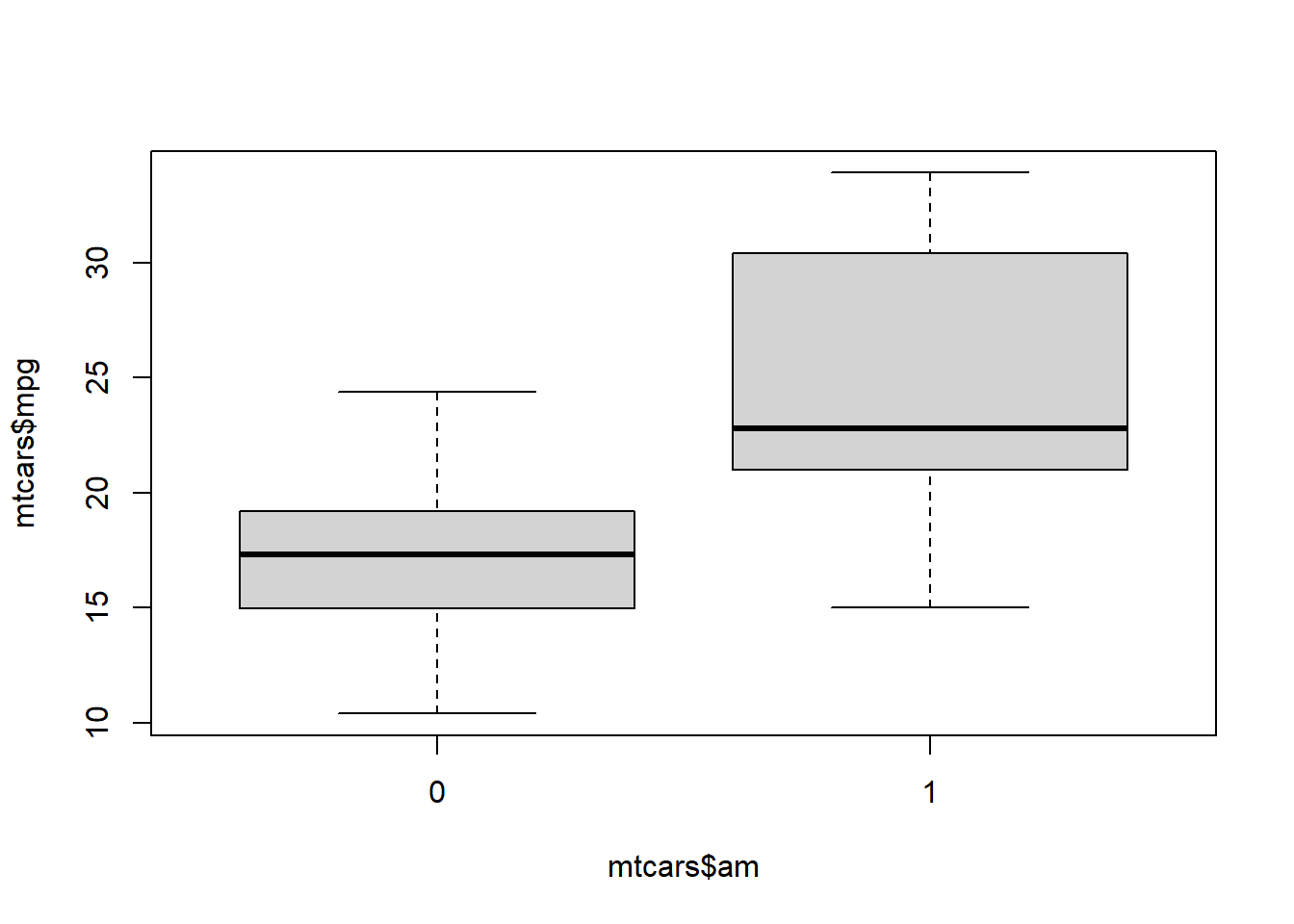
Das Getriebe scheint einen Einfluss auf den Verbrauch zu haben, ob dieser auch statistisch signifikant ist, könnte man zum Beispiel mit einem t-Test oder eben auch einer ANOVA testen.
Test <- aov(mpg~am,data = mtcars)
summary(Test)
## Df Sum Sq Mean Sq F value Pr(>F)
## am 1 405.2 405.2 16.86 0.000285 ***
## Residuals 30 720.9 24.0
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Der t-Test wird signifikant. Der Unterschied im Verbrauch ist also statistisch signifikant. Das heißt aber nicht unbedingt, dass das Getriebe auch ursächlich ist für den höheren Verbrauch. Hier hilft uns die ANCOVA.
Hypothese für die Kovariate
Es könnte sein, dass der Einfluss eigentlich durch die Motorleistung (hp) verursacht wird und bei gleichbleibender Leistung (hp) das Getriebe gar keinen Einfluss auf den Verbauch (mpg) hat.
Voraussetzungen prüfen
Die Voraussetzungen sind bei ANCOVA insbesondere Varianzhomogenität und Unabhängigkeit des Prädiktors von der Kovariate
Varianzhomogenität
Testen wir zunächst die Varianzhomogenität mit dem Levene-Test. Die Notation ist wie bisher, jedoch müssen wir die Variable Getriebe (am) als Faktor hinterlegen. Dies machen wir hier mit as.factor.
library(car)
leveneTest(mtcars$mpg, as.factor(mtcars$am))
## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 1 4.1876 0.04957 *
## 30
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Der Test wird knapp signifikant. Wir müssen unsere Ergebnisse also mit Vorsicht betrachten oder robuste Methoden nutzen. Da der Wert genau an der Grenze ist, machen wir an dieser Stelle mit der ANCOVA weiter.
Unabhängigkeit des Prädiktors von der Kovariate
Wir müssen die Frage beantworten, ob es auf den verschiedenen Stufen der UV (Getriebeart) statistisch signifikante Unterschiede in der Kovariate (Leistung) gibt
Hierzu führen wir eine ANOVA mit dem Prädiktor und der Kovariate aus.
ANOVA_Test<-aov(hp~am, data=mtcars)
summary(ANOVA_Test)
## Df Sum Sq Mean Sq F value Pr(>F)
## am 1 8619 8619 1.886 0.18
## Residuals 30 137107 4570Das Ergebnis zeigt, dass es keinen signifikanten Unterschied in der Leistung, abhängig vom Getriebe, gibt. Der Prädiktor (Getriebe) ist also von der Kovariate unabhängig.
ANCOVA durchführen
Wir wollen testen, ob der Einfluss auf den Verbrauch durch die Motorleistung (hp) verursacht wird und bei gleichbleibender Leistung (hp) das Getriebe gar keinen Einfluss auf den Verbauch (mpg) hat. Um diese Möglichkeit zu testen, führen wir eine ANCOVA durch und kontrollieren für die Leistung (hp).
Wir nutzen im nächsten Schritt das lineare Modell, welches wir mit lm aufrufen. Die gesamte Notation lautet: lm(AV~UVKovariate)*
ANCOVA_CARS <- lm(mpg~am*hp,data = mtcars)
summary(ANCOVA_CARS)
##
## Call:
## lm(formula = mpg ~ am * hp, data = mtcars)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.3818 -2.2696 0.1344 1.7058 5.8752
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 26.6248479 2.1829432 12.197 0.00000000000101 ***
## am 5.2176534 2.6650931 1.958 0.0603 .
## hp -0.0591370 0.0129449 -4.568 0.00009018507863 ***
## am:hp 0.0004029 0.0164602 0.024 0.9806
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.961 on 28 degrees of freedom
## Multiple R-squared: 0.782, Adjusted R-squared: 0.7587
## F-statistic: 33.49 on 3 and 28 DF, p-value: 0.000000002112Die Ergebnisse zeigen, dass nun, mit Kovariate, nur die Leistung (hp) einen signifikanten Einfluss auf den Verbrauch hat. Der Faktor Getriebe (am) hat nun keinen siginifikanten Einfluss auf den Verbrauch hat (mpg) mehr. Auch der Interaktionseffekt wird nicht signifikant.
Mit anderen Worten: Bei konstanter Leistung gibt es keinen signifikanten Unterschied im Verbrauch zwischen Fahrzeugen mit und ohne Automatikgetriebe.
Um besser zu verstehen, wie die Getriebe, die Leistung und der Verbauch zusammenhängen, erstellen wir ein Interaktionsdiagramm
Hierfür nutzen wir das Paket rockchalk
library(rockchalk)
slopes <-plotSlopes(ANCOVA_CARS,plotx="hp", modx="am")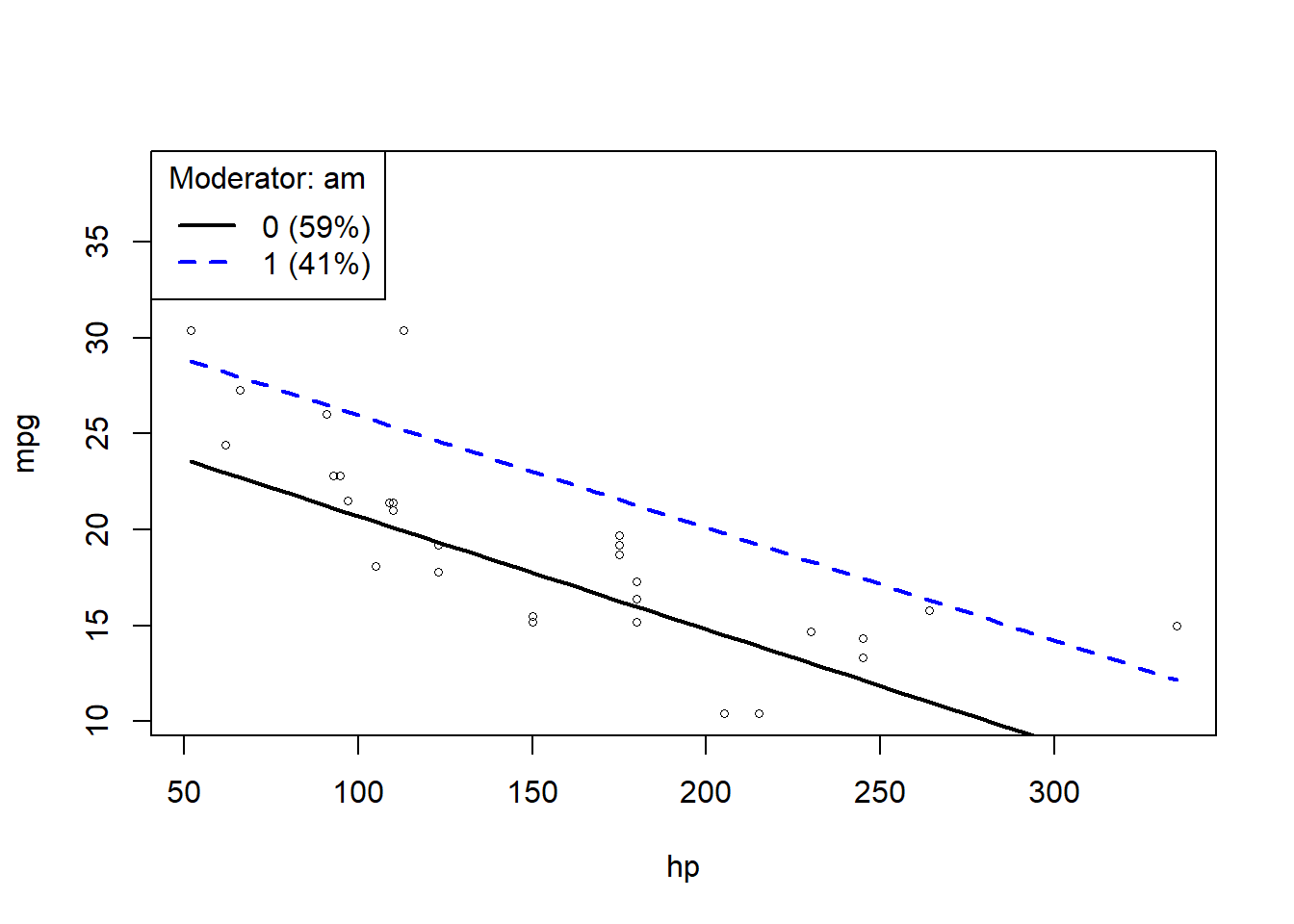
Das Diagramm zeigt, dass es keinen Interaktionseffekt gibt (Linien fast parallel), was wir auch in den Daten bereits gesehen haben. Das heißt, mit zunehmender Leistung nimmt der Verbrauch zu (mpg nimmt ab), unabhängig davon, ob manuelles oder Automatikgetriebe.
In diesem Video zeige ich, wie das in R funktioniert:

