Beispiel Messwiederholungs-ANOVA

Nehmen wir an, der Trinkfestigkeits-Versuch von eben wurde als Messwiederholungs-Design durchgeführt. Also haben alle Personen zunächst ohne die Wunderpille, dann mit einer und zuletzt mit zwei Pillen den Cannstatter Wasen besucht.

Daten laden:

Pille<-read.csv2(file="Pille.csv")

Deskriptive Analyse

Gibt es einen signifikanten Unterschied zwischen den 3 Messzeitpunkten? Schauen wir uns dies zunächst deskriptiv an und erzeugen einen Boxplot.

boxplot(Pille$Menge~Pille$Messzeitpunkt)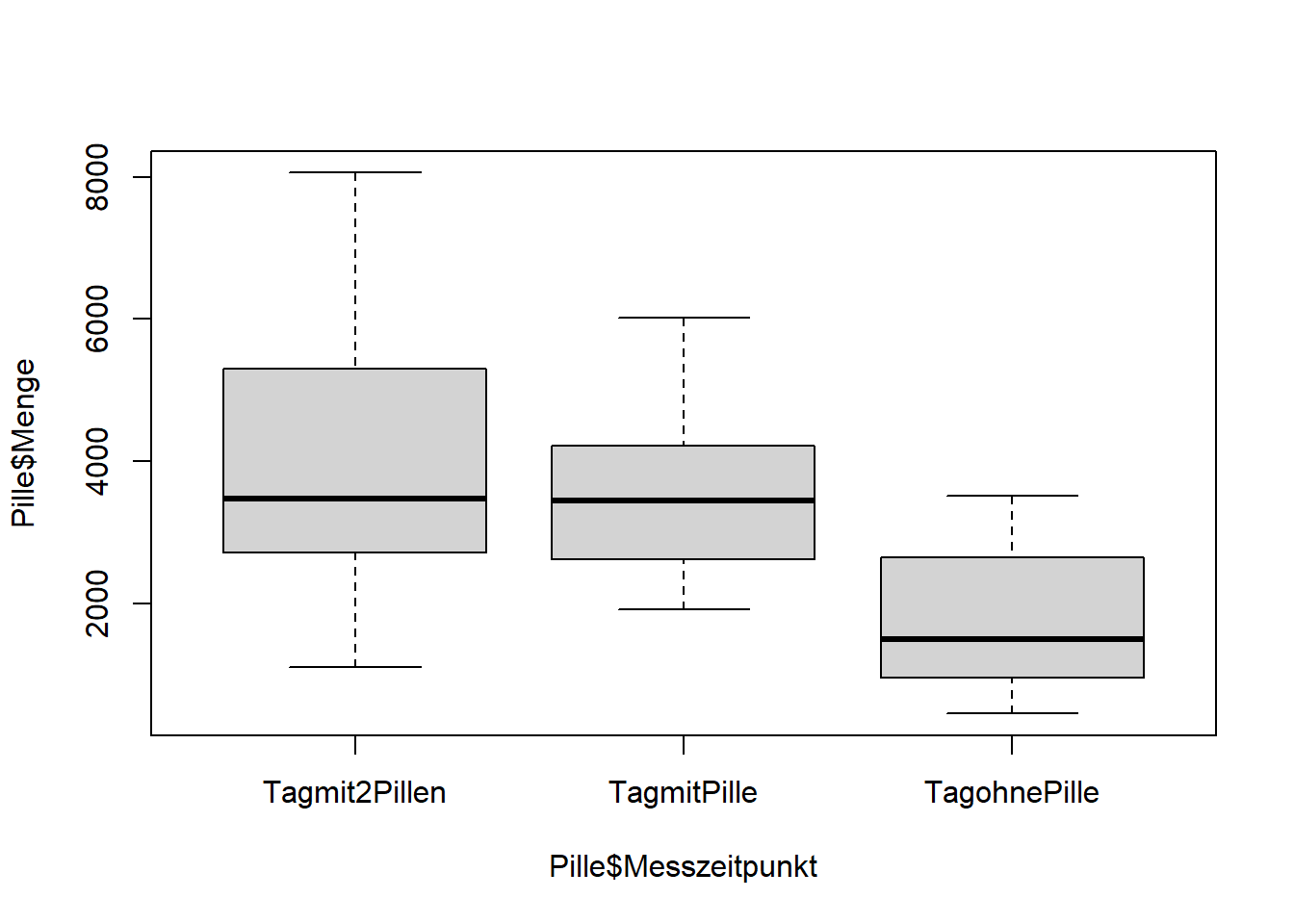

Voraussetzungen prüfen

Anders als bei der ANOVA für between designs, müssen wir hier nicht auf Varianzhomogenität zwischen den Merkmalsträgern prüfen. Jedoch gibt es eine ähnliche Voraussetzung, die geprüft werden muss, hier die Sphärizität. Die Sphärizität beschreibt die Varianzhomogenität zwischen den Messzeitpunkten (paarweise). Ist dies nicht gegeben, müssen die Freiheitsgrade korrigiert werden, dies wird meist mit der Greenhouse-Geisser oder Huynh-Feldt Methode gemacht.

Hierfür nutzen wir wieder die aov_car Funktion aus dem Paket afex. Hierbei wird automatisch Mauchly’s Test for Sphericity durchgeführt, wir brauchen also nicht extra Voraussetzungen prüfen. .

ANOVA Durchführen

Die Notation ist wie bisher, neu ist nun, dass wir beim Error() term zunächst die Identifikation der Person (Hier “ID”), dann die Identifikation des Messzeitpunkts (hier “Messzeitpunkt”) mit einem Querschnitt getrennt angeben müssen

ANOVA3 <- aov_car(Menge ~ Error(ID/Messzeitpunkt), data=Pille)
summary(ANOVA3)
## 
## Univariate Type III Repeated-Measures ANOVA Assuming Sphericity
## 
##                  Sum Sq num Df Error SS den Df F value      Pr(>F)
## (Intercept)   310215363      1 60792070      9  45.926 0.000081144
## Messzeitpunkt  29481007      2  8970660     18  29.577 0.000002047
##                  
## (Intercept)   ***
## Messzeitpunkt ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## 
## Mauchly Tests for Sphericity
## 
##               Test statistic  p-value
## Messzeitpunkt        0.46318 0.046027
## 
## 
## Greenhouse-Geisser and Huynh-Feldt Corrections
##  for Departure from Sphericity
## 
##               GG eps Pr(>F[GG])    
## Messzeitpunkt 0.6507 0.00008217 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##                 HF eps    Pr(>F[HF])
## Messzeitpunkt 0.715319 0.00004133513

Das Ergebnis zeigt, dass die Annahme der Sphärizität verletzt ist (Mauchly’s Test ist signifikant). Daher betrachten wir die Greenhouse-Geisser oder Huynh-Feldt korrigierten Werte. Wir sehen, dass der Unterschied zwischen mindestens zwei Messzeitpunkten signifikant ist, wissen aber wieder nicht, wo genau signifikante Unterschiede sind. Daher führen wir nun Post-Hoc-Verfahren durch.

Post-Hoc-Verfahren

Bei Messwiederholungs-ANOVA kann das Paket emmeans für Post-hoc-Analysen verwendet werden. Das Paket “emmeans” (geschätzte marginale Mittelwerte) ermöglicht es Ihnen, geschätzte marginale Mittelwerte für jede Ebene der Faktoren in Ihrem ANOVA-Modell zu erhalten und sie mit einer Vielzahl verschiedener Tests zu vergleichen. Wir nutzen für die Paarvergleiche die Funktion pairs.

PostHocPille <- emmeans(ANOVA3, specs="Messzeitpunkt")
pairs(PostHocPille)
##  contrast                     estimate  SE df t.ratio p.value
##  TagohnePille - TagmitPille      -1854 208  9  -8.915  <.0001
##  TagohnePille - Tagmit2Pillen    -2285 410  9  -5.574  0.0009
##  TagmitPille - Tagmit2Pillen      -431 296  9  -1.455  0.3556
## 
## P value adjustment: tukey method for comparing a family of 3 estimates

Wir sehen, dass es zwischen dem Messzeitpunkt 1 (ohne Pille) und dem Messzeitpunkt 2 (mit Pille) einen signifikanten Unterschied gibt, wie auch zwischen Messzeitpunkt 1 und 3 (mit 2 Pillen). Der Messzeitpunkt 2 (mit Pille) unterscheidet sich jedoch nicht signifikant vom Messzeitpunkt 3 (mit 2 Pillen). Wir können daher keine Empfehlung dafür aussprechen, zwei Pillen zu nehmen anstatt nur einer (von den Nebenwirkungen natürlich mal abgesehen).

Grafische Darstellung

Um eine Darstellung der 3 Messzeitpunkte mit jeweiligem Konfidenzintervall zu erhalten, nutzen wir wieder die afex_plot und ergänzen error=“within” (Hierdurch erhalten wir den Vergleich zwischen den 3 Messzeitpunkten).

afex_plot(ANOVA3, x="Messzeitpunkt", error="within")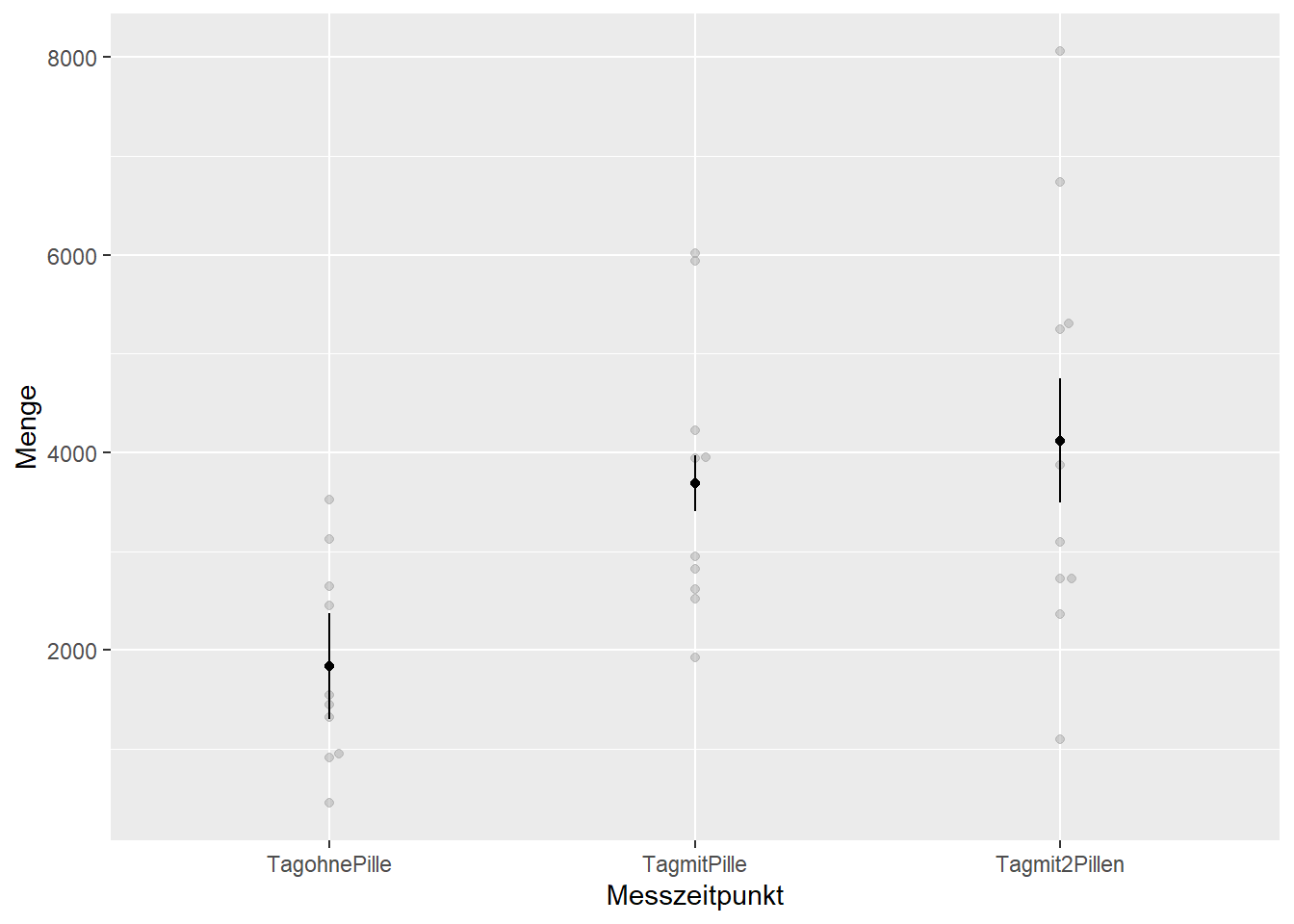

In diesem Video zeige ich, wie das in R funktioniert:

Übung

In einer Studie haben Nolen-Hoeksema and Morrow (1991) die Depressionsneigung von Studierenden, zwei Wochen vor einem schweren Erdbeben in Kalifornien in 1987 und an 4 weiteren Zeitpunkten jeweils 2 Wochen später gemessen.

Wir laden die Daten

Depression <- read.csv("NolenHoeksema.csv")
Depression$time <- as.factor(Depression$time)
Depression$Subject <- as.factor(Depression$Subject)


Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.