Statistik mit R & RStudio
29 Einfache lineare Regression mit R
Einfache lineare Regression
Das Ziel der bivariaten linearen Regression ist es, die am besten passende Linie oder Regressionsgerade zu finden, die die Beziehung zwischen den beiden Variablen beschreibt. Die Regressionsgerade dient zur Vorhersage des Wertes einer Variablen auf der Grundlage des Wertes einer anderen Variablen. Hierbei werden die beiden Variablen als Prädiktor bzw. unabhängige Variable und als Kriterium bzw. abhängige Variable bezeichnet.
Die Gleichung für eine bivariate lineare Regressionsgerade ist
y = b0 + b1 * x
wobei y die abhängige Variable, x die unabhängige Variable, b0 der y-Achsenabschnitt und b1 die Steigung der Linie ist. Die Steigung b1 gibt die Änderung von y bei einer Änderung von x um eine Einheit an, während der y-Achsenabschnitt b0 den Wert von y darstellt, wenn x gleich Null ist.
Um die beste Anpassungslinie (Regressionsgerade) zu ermitteln, wird die Methode der kleinsten Quadrate verwendet. Mit dieser Methode wird die Linie gefunden, die die Summe der quadrierten Differenzen zwischen den vorhergesagten Werten von y und den tatsächlichen Werten von y minimiert. Die Werte von b0 und b1, die diese Summe minimieren, gelten als die besten Schätzungen für die wahren Werte dieser Parameter. Anders ausgedrückt ist dies auch die Linie, die den geringsten (quadrierten) Abstand zu allen Punkten im Streudiagramm hat.
Sobald die beste Regressionsgerade bestimmt wurde, kann sie verwendet werden, um Vorhersagen über die abhängige Variable auf der Grundlage neuer Werte der unabhängigen Variable zu treffen. Dazu setzt man den neuen Wert von x in die Gleichung für die Regressionsgerade ein und löst für y auf. Die Bestimmung der Regressionsgerade als auch die Vorhersage übernimmt natürlich R für uns.
Vorbereitungen
Zunächst laden wir die für dieses Kapitel notwendigen Pakete
library(psych)
library(Hmisc)
library(car)Wissenschaftliche Notation ausschalten (damit fällt es uns leichter den Output zu interpretieren, da Nachkommastellen nicht umgewandelt werden).
options(scipen = 999)Daten vorbereiten
Wir starten mit einem einfachen Beispiel: Lässt sich die Koerpergroesse aus der Schuhgroesse vorhersagen?
Wir laden unseren WPStudis Datensatz und erstellen zunächst ein Subset mit den relevanten Variablen und schließen NAs aus, da fehlende Werte (NAs) zu einer Fehlermeldung bei der Berechnung der Regressionsgerade führen.
load("WPStudis.Rdata")
data_lm <- na.omit(WPStudis[c("F1_Nummer", "F4_Koerpergroesse","F5_Schuhgroesse","F2_Alter", "F3_Geschlecht")])Modell erstellen
In R kann eine bivariate lineare Regression mit der Funktion lm() durchgeführt werden, was für “lineares Modell” steht. Die grundlegende Syntax für diese Funktion lautet wie folgt:
lm(y ~ x, Daten)
wobei y der Name des Kriteriums bzw. der abhängigen Variable ist und x der Name des Prädiktors bzw. der unabhängigen Variablen. Durch die Funktion wird ein lineares Modellobjekt namens erstellt, das die Koeffizienten und andere Informationen über die Regression enthält. Dieses speichern wir unter einem neuen Objektnamen ab, den Sie natürlich frei wählen können. Wir nennen dieses nun “lm1”, der Syntax sieht dann wie folgt aus:
lm1<- lm(F4_Koerpergroesse ~ F5_Schuhgroesse, data=data_lm)
lm1
##
## Call:
## lm(formula = F4_Koerpergroesse ~ F5_Schuhgroesse, data = data_lm)
##
## Coefficients:
## (Intercept) F5_Schuhgroesse
## 93.425 1.936Interpretation
Aus den beiden Werten lässt sich die Regressionsgleichung (also die Formel für eine Vorhersage) ableiten. Intercept entspricht b0, also der Konstante oder auch dem Punkt, an dem die Gerade die y-Achse schneidet. Der Wert unter “F5_Schuhgroesse” entspricht b1, also dem Regressionsgewicht oder auch der Steigung der Geraden.
Die resultierende Regressionsgleichung ist nun also:
y (Körpergröße) = 93,43 + 1,94 * x (Schuhgröße).
Testen Sie doch mal für Ihre Schuhgröße, wie gut diese Vorhersage funktioniert. Der Wert 1,94 ist die Steigung der Regressionsgerade und sagt uns daher, wie der Zusammenhang verläuft. Da dieser Verlauf jedoch stark von der zugrundeliegeneden Skala abhängt, können wir diesen auch standardisieren. Die standardisierten Koeffizienten (= betas) können mit der scale-Funktion ausgegeben werden:
lm2<- lm(scale(F4_Koerpergroesse) ~ scale(F5_Schuhgroesse), data=data_lm)
lm2
##
## Call:
## lm(formula = scale(F4_Koerpergroesse) ~ scale(F5_Schuhgroesse),
## data = data_lm)
##
## Coefficients:
## (Intercept) scale(F5_Schuhgroesse)
## -0.0000000000000005575 0.7230085486694098895Was bedeutet der standardisierte Koeffizient / beta Wert bei der bivariaten Regression?
Grundsätzlich helfen standardisierte Koeffizienten (beta Werte) bei der Interpretation, da sie unabhängig von der zugrunde liegenden Skala interpretierbar sind. Bei der bivariaten Regression entspricht der Wert dem Korrelationskoeffizienten und sagt uns daher, wie stark der Zusammenhang ist (unabhängig von der Skala).
Zum Vergleich können wir die Korrelation der beiden Variablen berechnen.
cor(data_lm$F4_Koerpergroesse,data_lm$F5_Schuhgroesse)
## [1] 0.7230085Signifikanztests und Gütemaße
Wie gut ist die Vorhersage für Ihre persönliche Körpergröße? Um diese Frage zu beantworten, benötigen wir Signifikanztests für die Regressionskoeffizienten und Gütemaße für das Regressionsmodell.
Die Funktion summary() liefert eine detaillierte Zusammenfassung des linearen Modellobjekts, das mit der Funktion lm() erstellt wurde.
summary(lm1)
##
## Call:
## lm(formula = F4_Koerpergroesse ~ F5_Schuhgroesse, data = data_lm)
##
## Residuals:
## Min 1Q Median 3Q Max
## -28.2497 -3.0276 0.1153 3.0041 15.1153
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 93.425 7.735 12.078 < 0.0000000000000002
## F5_Schuhgroesse 1.937 0.195 9.929 0.000000000000000402
##
## (Intercept) ***
## F5_Schuhgroesse ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.394 on 90 degrees of freedom
## Multiple R-squared: 0.5227, Adjusted R-squared: 0.5174
## F-statistic: 98.58 on 1 and 90 DF, p-value: 0.000000000000000402Die Zusammenfassung enthält in der Regel die folgenden Informationen:
Call: Gibt das Modell an, das verwendet wurde, einschließlich des Namens der abhängigen Variable, der unabhängigen Variable(n) und der verwendeten Daten.
Residuen: Die Residuen des Modells, d. h. die Differenzen zwischen den beobachteten Werten der abhängigen Variablen und den vorhergesagten Werten der abhängigen Variablen. Die Zusammenfassung enthält die Standardabweichung der Residuen, die ein Maß für die Streuung der Residuen um den Mittelwert ist, sowie die minimalen und maximalen Residuenwerte.
Koeffizienten: Die Koeffizienten des Modells, d. h. die Schätzungen der Parameter der Regressionsgeraden. Die Tabelle enthält die Schätzungen der Koeffizienten, ihre Standardfehler, t-Werte und p-Werte.
R-Quadrat: Das Bestimmtheitsmaß (auch Determinationskoeffizient) ist ein Maß für den Anteil der Variation in der abhängigen Variable, der durch die unabhängige Variable erklärt wird. Es reicht von 0 bis 1, und kann in Prozent interpretiert werden. So kann ein Wert von 0,4 so interpretiert werden, dass 40 % der Variation der abhängigen Variablen durch die unabhängigen Variablen erklärt wird.
F-Statistik: Die F-Statistik und ihr zugehöriger p-Wert, der prüft, ob das lineare Modell insgesamt signifikant ist.
Signifikanz-Codes: Ein Code, der das Signifikanzniveau der Koeffizienten angibt. Ein Code von “***” bedeutet zum Beispiel, dass der Koeffizient auf dem Niveau von 0,001 signifikant ist.
In diesem Fall sehen wir, dass die Schuhgröße ein signifikanter Prädiktor für die Körpergröße ist (p < .000). Ausserdem erhalten wir den Determinationskoeffizienten R2 von 0,51 (korrigierten Wert nehmen). Wir können also sagen, dass wir 51 % der Varianz in der Körpergröße durch die Schuhgröße vorhersagen können. Des Weiteren erhalten wir einen F-Wert, hier 98 (1,90), den wir inhaltlich nicht interpretieren können (sollte jedoch größer 1 sein).
Die einzelnen Komponenten des lm-Objekts lassen sich auch einzeln auslesen:
coefficients(lm1) #Modelkoeffizienten
## (Intercept) F5_Schuhgroesse
## 93.425002 1.936493
confint(lm1, level=0.95) #Konfidenzintervalle
## 2.5 % 97.5 %
## (Intercept) 78.057622 108.792382
## F5_Schuhgroesse 1.549008 2.323979
residuals(lm1) #Residuen
## 1 2 3 4 5
## -7.94824817 9.11525833 -1.01175467 -28.24967664 3.05175183
## 6 7 8 9 10
## 0.05175183 0.92473882 2.05175183 -5.07526118 5.11525833
## 11 12 13 14 15
## -2.07526118 -1.94824817 5.17876484 -5.94824817 4.92473882
## 16 17 18 19 20
## -3.13876768 -3.69422216 4.05175183 -7.01175467 0.49629735
## 21 22 23 24 25
## -3.94824817 -1.07526118 7.05175183 -2.88474167 0.11525833
## 26 27 28 29 31
## -3.01175467 -0.94824817 1.98824533 2.92473882 2.92473882
## 32 33 34 35 36
## 2.43279085 -8.07526118 0.11525833 6.05175183 3.92473882
## 37 38 39 40 41
## 1.98824533 2.49629735 8.30577784 -0.88474167 1.05175183
## 42 43 44 45 46
## -1.82123516 0.17876484 4.49629735 -3.13876768 -3.13876768
## 47 48 49 50 51
## 1.86123232 -2.07526118 6.24227134 3.24227134 -1.01175467
## 52 53 54 55 56
## 6.11525833 1.92473882 0.30577784 5.11525833 6.05175183
## 57 58 59 60 61
## 1.36928434 5.30577784 5.05175183 -3.07526118 -0.94824817
## 62 63 64 65 66
## 1.11525833 -2.82123516 -0.56720915 2.43279085 -1.82123516
## 67 68 69 70 71
## -3.13876768 -0.94824817 -1.07526118 -0.63071566 0.62331035
## 72 73 74 75 76
## -1.94824817 -2.07526118 4.36928434 15.11525833 -1.01175467
## 77 78 79 80 81
## 7.11525833 -5.88474167 2.05175183 -7.01175467 3.92473882
## 82 83 84 85 86
## -3.13876768 -4.01175467 -4.01175467 -8.07526118 -3.94824817
## 87 88 89 90 91
## -10.07526118 -3.88474167 2.98824533 -7.07526118 1.11525833
## 92 93
## 0.92473882 9.92473882Voraussetzung prüfen
Was wir aber eigentlich vor der Regression machen sollten, ist die Voraussetzung für die Regression zu prüfen.
Die wesentlichen Voraussetzungen für die lineare Regression sind:
- Korrekte Spezifikation des Modells
- Normalverteilung der Residuen
- Homoskedastizität
- Ausreißer und einflussreiche Datenpunkte
Bei multipler Regression (also bei mehr als einem Prädiktor) gelten zusätzlich folgende Voraussetzungen:
- Multikollinearität
- Unabhängigkeit der Residuen
Über Plots lassen sich die Voraussetzungen 1 bis 4 relativ einfach visuell prüfen, hierzu wenden wir die Funktion plot() auf das Modell an. In diesem Fall werden uns vier Grafiken ausgegeben. Wenn Sie alle 4 Graphen auf einer Seite sehen wollen, können Sie mit par(mfrow=c(2,2)) die Anzeige des Plot-Fensters auf vier Grafiken einstellen (2 nebeneinander, 2 übereinander). Dies können Sie über dev.off() wieder zurücksetzen.
par(mfrow=c(2,2))
plot(lm1)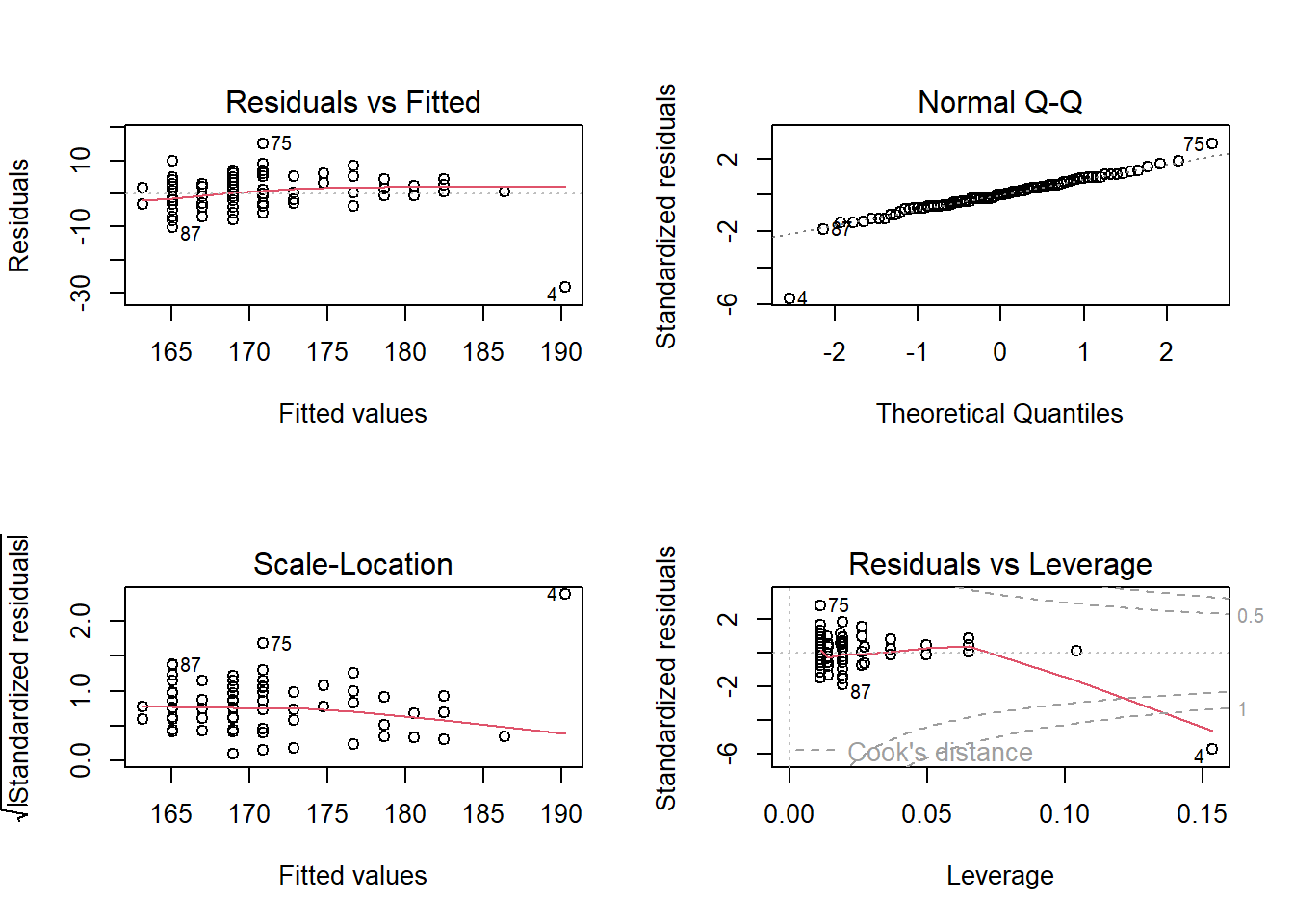
Erklärung der Plots:
– Residuals vs. Fitted: Testet Voraussetzung 1 – Die Werte sollen unsystematisch verteilt und die rote (Lowess-Linie) möglichst parallel zur x-Achse verlaufen
– Normal-Q-Q: Testet Voraussetzung 2 – Normalverteilte Residuen sollten relativ nah auf der Diagonalen liegen
– Scale-Location-Diagram: Testet Voraussetzung 3 – Homoskedastizität ist gegeben bei unsystematischer Verteilung der Residuen. Insbesondere sollten wir hier darauf achten, dass die Residuen nicht “trichterartig” in die eine oder andere Richtung zunehmen.
– Residuals vs. Leverage: Testet Voraussetzung 4 – Diese Darstellung zeigt uns die Ausreiser, besonders kritisch sind dabei alle Werte, die ausserhalb von Cooks Distance liegen (gepunktete Linie). Die Ziffern neben den Punkten sind die Zeilennummern in den Daten. Wir sollten uns also die angezeigte Zeilennummer 4 in den Daten nochmal ansehen und den Wert ggf. aussschließen.
In diesem Video zeige ich, wie das in R funktioniert:
Übung
Wir haben uns entschlossen, den Outlier in Zeile 4 rauszunehmen. Rechnen Sie die Analysen nochmal ohne diesen Wert durch. Was hat sich verändert?
Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.
Scatterplot mit Regressionsgerade
Wir wollen zum Abschluss die Regression noch grafisch in einem Streudiagramm darstellen.
plot(data_lm$F5_Schuhgroesse,data_lm$F4_Koerpergroesse,
ylab="Körpergroesse",
xlab="Schuhgroesse")
abline(lm1) #Einzeichnen der Regressionsgerade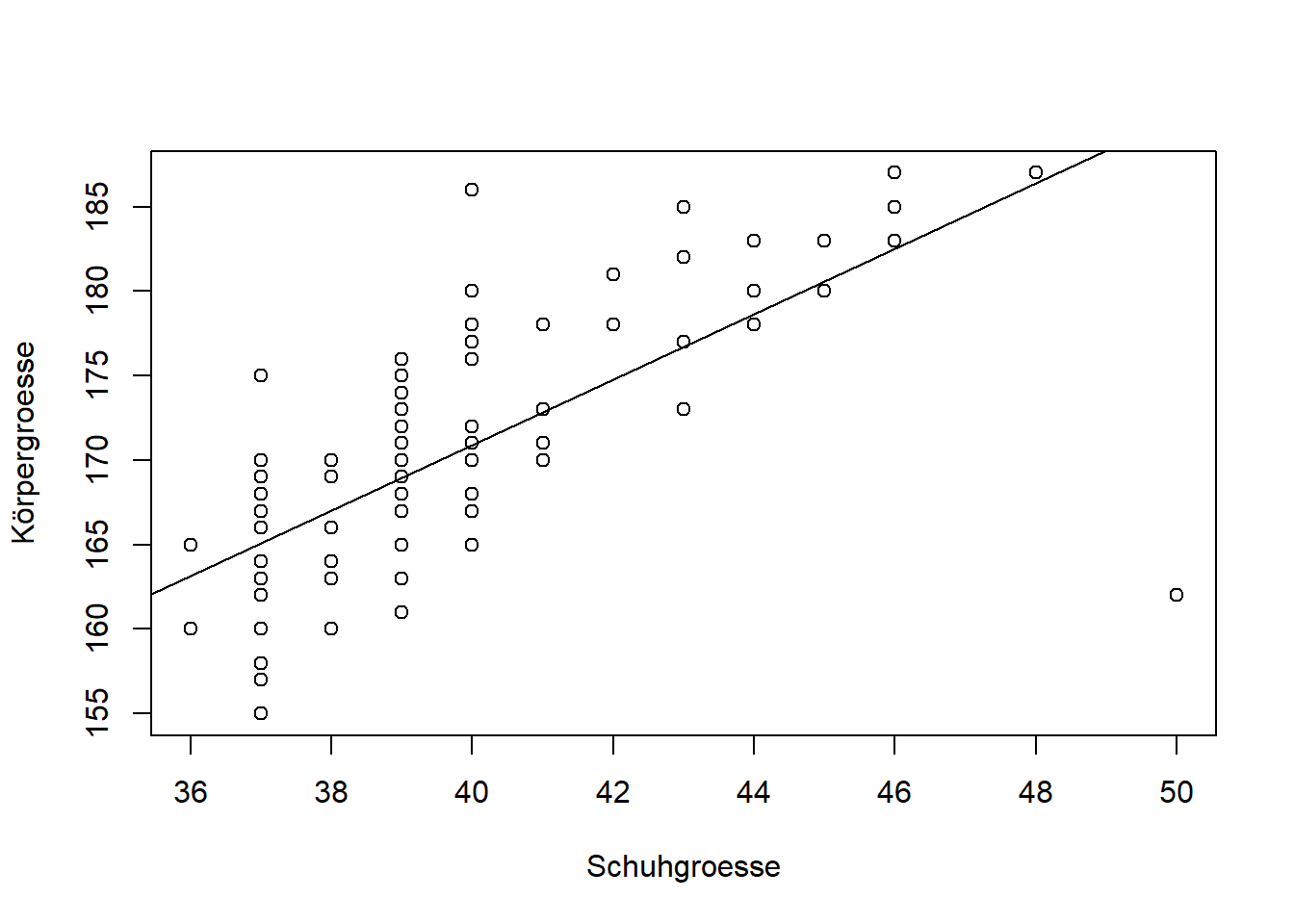
Vorhersagen erstellen
Wir können nun mit einem beliebigen Wert für Schuhgroesse, die Koerpergroesse vorhersagen. Hierzu nutzen wir die predict() Funktion. Sie benötigt zwei Hauptargumente: den Namen des Modellobjekts und die neuen Daten, für die Sie Vorhersagen machen möchten.
Die grundlegende Syntax für die Funktion predict() lautet wie folgt:
predict(modell, newdata)
Dabei ist model der Name des linearen Modellobjekts, das mit der Funktion lm() erstellt wurde, und newdata ist ein dataframe, der die neuen Werte der unabhängigen Variablen enthält, für die Sie Vorhersagen treffen wollen. Daher müssen wir für newdata immer die data.frame Funktion nutzen, auch wenn wir, wie in diesem Beispiel, nur einen einzelnen Vorhersagewert haben.
Wir wollen die Koerpergroesse für eine Person mit Schuhgroesse 42 vorhersagen. Sie können den Wert 42 dabei gerne auf Ihre Schuhgroesse anpassen und sehen, welche Vorhersage das Modell für Sie treffen würde.
predict(lm1, data.frame(F5_Schuhgroesse=42))
## 1
## 174.7577In diesem Video zeige ich, wie das in R funktioniert:
Übung
Wir nutzen das Data-Set “Prestige” aus dem Package car. Schauen Sie sich die Daten an und machen Sie sich damit vertraut (?Prestige)
- Können wir aufgrund der Bildung (Anzahl Jahre) das Einkommen ableiten?
- Wie lautet die Regressionsgerade? Wie interpretieren Sie den B-Koeffizient?
- Zeichnen Sie diese in den Scatterplot ein.
- Wie hoch ist, basierend auf Ihrem Modell, das vorhergesagte Einkommen bei 12 Jahren Bildung?
Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.
Übung
Wir nutzen das Data-Set “happymoney”. Hier sehen wir den Zusammenhang zwischen dem durchschnittlichen Vermögen pro Einwohner verschiedener Länder und dem Glücksindex der Einwohner basierend auf dem World Happiness Report. (Quelle Global Wealth Book 2021 von Credit Suisse https://www.credit-suisse.com/media/assets/corporate/docs/about-us/research/publications/global-wealth-databook-2021.pdf)
- Können wir sagen, dass in Ländern mit höherem Pro-Kopf-Vermögen auch die glücklicheren Menschen wohnen? Stellen Sie den Zusammenhang in einem Streudiagramm dar und zeichnen Sie eine Regressionsgerade ein.
- Wieviel Euro höheres Pro-Kopf-Vermögen ist notwendig für eine Steigerung des Glücksindex um 1 Punkt zu erreichen?
Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.



