Chi-Quadrat-Tests

Patrick Planing

Hypothesentests

12 Chi-Quadrat-Tests

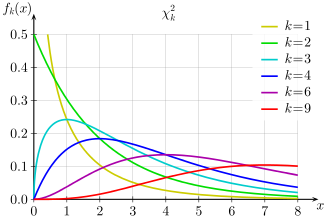
12.0 Einführung χ2-Verteilung

Wohnen in Stuttgart mehr Vegetarier als im Bundesdurchschnitt? Hängt die Ernährungsart vom Geschlecht ab? Um solche und ähnliche Fragen mit nominal skalierten Variablen beantworten zu können, wollen wir in diesem Kapitel unseren Methodenkoffer erweitern um die Gruppe der Chi²-Tests. Diese Tests unterscheiden sich vom Z-Test, den Sie im vorausgegangenen Kapitel kennengelernt haben, dadurch, dass sie nicht die Standardnormalverteilung, sondern die χ²-Verteilung für die Ableitung von Auftretenswahrscheinlichkeiten zugrunde legen. Die Chi-Quadrat-Verteilung (χ²-Verteilung) ergibt sich aus der Standardnormalverteilung. Liegen n voneinander unabhängige standardnormalverteilte Zufallsvariablen (Z₁, Z₂, .. , Z_n) vor und werden diese jeweils quadriert, so folgt daraus die sogenannte χ²-Verteilung (Chi-Quadrat-Verteilung).

Die Anzahl n der Zufallsvariablen wird durch die sog. Freiheitsgrade festgelegt, auf die wir gleich noch eingehen. Anders als bei der Standardnormalverteilung, gibt es nicht die eine χ2-Verteilung, sondern die Form der χ2-Verteilung wird durch die Freiheitsgrade eindeutig festgelegt. Die unten stehende Grafik zeigt die χ2-Verteilung beispielhaft für 1-9 Freiheitsgrade.

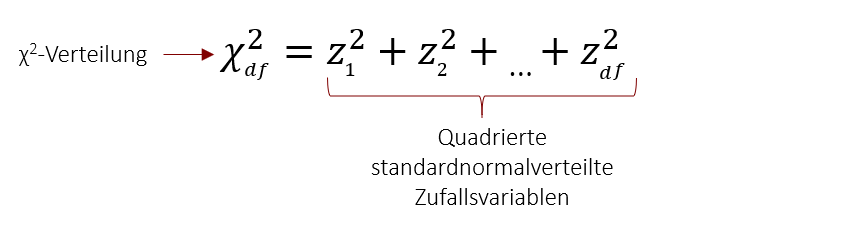
Expertenwissen: Chi-Quadrat-Verteilung

Mit größer werdenden Freiheitsgraden (df) nähert sich die χ2-Verteilung der Normalverteilung an mit dem Mittelwert 𝜇 =n und der Standardabweichung 𝜎=√2𝑑𝑓.

Video 12.1 Chi-Quadrat-Tests für Nominaldaten | Einführung

12.1 Freiheitsgrade

Freiheitsgrade bestimmen, wie viele Werte in einer Berechnungsformel für einen Kennwert bzw. Parameter frei variieren dürfen, damit es genau zu einem bestimmten Ereignis bzw. Wert kommt. Wenn ich eine Summe aus n Werten berechnen will, dann habe ich n-1 Freiheitsgrade. Wenn ich also drei Werte aufsummiere und die ersten beiden Werte sowie die Summe sind bekannt, dann steht auch der dritte Wert fest. Die Genauigkeit, mit der Stichprobenwerte Populationsparameter schätzen, hängt von der Zahl der Freiheitsgrade ab. Dadurch beeinflussen die Freiheitsgrade auch die Form solcher Verteilungen, in deren Berechnung geschätzte Größen eingehen.

Beispiele Freiheitsgrade

Geschlecht:

Ist bekannt, wie viele Studenten in einem Kurs sind, so reicht es zu wissen, wie viele Frauen im Kurs sind. Die Anzahl der männlichen Kursteilnehmer steht damit fest. Also 2-1 = 1 Freiheitsgrad.

Sternzeichen:

Habe ich in einem Kurs mit bekannter Teilnehmerzahl 11 (frei gewählte) Sternzeichen abgefragt, so ist dies ausreichend um die Häufigkeiten aller 12 Sternzeichen zu bestimmen. Die Häufigkeit des „übrigen“ Sternzeichens ergibt sich aus der Summe abzüglich der Häufigkeit aller anderen 11 Sternzeichen. Also 12-1 = 11 Freiheitsgrade

Video 12.2 Chi-Quadrat-Tests für Nominaldaten | Freiheitsgrade

12.2 Übersicht Chi-Quadrat Tests

Bei Daten mit Nominalskalen-Niveau macht es keinen Sinn, Kennwerte der zentralen Tendenz (z.B. Mittelwert) oder der Streuung (z.B. Varianz) zu betrachten. Der Fokus der Analysen liegt daher auf den Häufigkeiten. Grundsätzlich gibt es zwei Arten von Fragestellungen, die wir bei Nominaldaten mit Hilfe von Chi-Quadrat-Tests überprüfen können:

Verteilungsform einer Variablen: Entspricht die Häufigkeit einer Variablen einem erwarteten Wert?
Zum Beispiel: Haben wir mehr Raucher bei unseren Studenten als der Bundesdurchschnitt?
Hierfür können wir den Chi-Quadrat Anpassungstest anwenden.
Unabhängigkeit von zwei Variablen: Gibt es einen Zusammenhang zwischen zwei nominalen Variablen oder sind diese unabhängig?
Zum Beispiel: Ist das Rauchverhalten unabhängig vom Geschlecht der Studierenden?
Hierfür können wir den Chi-Quadrat Unabhängigkeitstest anwenden

Auf beide Arten des Chi-Quadrat Test werden wir im Folgenden näher eingehen.

12.3 Der Chi-Quadrat Anpassungstest

Bei den sogenannten χ2-Verfahren wird überprüft, ob beobachtete Häufigkeitsverteilungen mit erwarteten Häufigkeitsverteilungen übereinstimmen, wobei die erwarteten Häufigkeiten die jeweilige Nullhypothese repräsentieren. Mit einem χ2-Anpassungstest (Goodness-of-fit-Test) wird geprüft, ob eine Stichprobe aus einer unterstellten (theoretischen) Verteilung stammt. Wenn Sie beispielsweise eine repräsentative Stichprobe aus der Bevölkerung ziehen wollen, so sollte die Geschlechterverteilung in der Stichprobe ausgeglichen sein (das wären Ihre erwarteten Häufigkeiten). Wenn nun die tatsächlichen (beobachteten) Häufigkeiten in der Stichprobe davon abweichen und Sie beispielsweise 55 Frauen und nur 45 Männer in der Stichprobe haben, können Sie dann noch von einer repräsentativen Stichprobe (in Bezug auf das Merkmal Geschlecht) sprechen? Genau hierauf kann Ihnen der χ2-Anpassungstest eine Antwort geben. Der Test berechnet, wie wahrscheinlich es ist, eine solche Abweichung unter Annahme der Nullhypothese zu erhalten – also unter der Annahme, dass Sie tatsächlich eine reine Zufallsstichprobe aus der Bevölkerung gezogen haben. Der resultierende χ2-Wert gibt Ihnen dabei ein Maß für die Abweichung des beobachteten Werts vom erwarteten Wert. Ist der χ2-Wert unter Annahme der Nullhypothese hinreichend unwahrscheinlich (z.B. die Wahrscheinlichkeit unter 5%), so wird die Nullhypothese verworfen und die Alternativhypothese angenommen. In diesem Fall haben Sie also keine repräsentative Stichprobe vorliegen. Neben dem Test auf Repräsentativität von Merkmalen kann der Test aber auch in vielen anderen Anwendungsgebieten zum Einsatz kommen. Sie können damit z.B. auch die eingangs gestellte Frage, ob in Stuttgart mehr Vegetarier als im Bundesdurchschnitt wohnen, beantworten. Vorrausetzung dafür ist jedoch immer, dass die Häufigkeit in der Population bekannt ist. Sie sollten also wissen, wie viel Prozent der Bundesbevölkerung Vegetarier sind. Der Test kann grundsätzlich mit allen nominal skalierten Variablen aber auch mit höher skalierten Merkmalen durchgeführt werden, wenn diese klassiert werden (also das Alter z.B. in Altersgruppen eingeteilt wird). Die Test-Hypothesen sind dabei grundsätzlich formal festgelegt und lauten:

H₀: Die Verteilung der Stichprobe entspricht der Verteilung der Population.
H₁: Die Verteilung der Stichprobe entspricht nicht der Verteilung der Population.

Dabei kann die in der H₀ vorgegebene theoretische Verteilung für jede Merkmalsausprägung eine spezifische erwartete Häufigkeit annehmen (also neben 50:50, auch 60:40 etc.). Die Hypothesen sind dabei immer ungerichtet. Da durch das Quadrieren im Chi²-Verfahren das Vorzeichen verloren geht, können keine gerichteten Tests durchgeführt werden.

Mögliche Hypothesen für χ2-Anpassungstests

Wir wollen testen, ob die Geschlechterverteilung der Statistik-Fans der Geschlechterverteilung der Bevölkerung entspricht:

H₀: Die Geschlechterverteilung der Statistik-Fans ist gleich 50:50
H₁: Die Geschlechterverteilung der Statistik-Fans ist ungleich 50:50.

Wir wollen testen, ob unsere Burgerkunden den normalen Fastfood Kunden entsprechen, von denen wir wissen, dass sie zu 60% männlich sind:

H₀: Die Geschlechterverteilung unserer Kunden ist gleich 60:40 (60% Männer, 40% Frauen)
H₁: Die Geschlechterverteilung unserer Kunden ist ungleich 60:40.

Wir wollen testen ob die Klausur im 1. „Corona-Semester“ schlechter ausgefallen ist als sonst und wir wissen, dass im langjährigen Durchschnitt 70% bestehen.

H₀: Die Anzahl bestandener Prüfungen im Studiengang ist 70%
H₁: Die Anzahl bestandener Prüfungen im Studiengang ist nicht 70% (weicht vom langjährigen Durchschnitt ab)

Video 12.3 Chi-Quadrat Anpassungstest | Hypothesenbildung

12.4 Berechnung Chi-Quadrat Anpassungstest

Wie können wir nun entscheiden, ob die H₀ verworfen werden kann und damit die H₁ die bessere Erklärung für die gefunden Daten ist? Der Schlüssel hierfür ist der χ2-Wert, der ja ein Maß für die Abweichung des beobachteten Werts vom erwarteten Wert darstellt. Je größer dieser Wert ist, desto größer die Abweichung vom erwarteten Wert und desto geringer die Wahrscheinlichkeit, dass es sich bei dieser Abweichung nur um einen Zufall handelt. Das ist die bestechend einfache Logik des χ2-Anpassungstest. Doch wie berechnet man nun den χ2-Wert und die daraus resultierende Wahrscheinlichkeit der Daten unter Annahme der H₀?

Im Folgenden wollen wir dies Schritt für Schritt angehen:

Schritt 1: Bestimmung der Häufigkeiten

Um den χ2-Wert zu bestimmen, benötigen wir zunächst die Häufigkeiten der jeweiligen Kategorien i, dies sind im Beispiel der Geschlechterverteilung die Kategorien „männlich“ und „weiblich“. Im Folgenden werden wir uns nur mit solchen dichotomen Variablen beschäftigen. Theoretisch kann der χ2-Anpassungstest aber genauso für Variablen mit mehr Ausprägungen gerechnet werden. Die benötigten Häufigkeiten sind also:

f_bi = beobachtete Häufigkeit in Kategorie i

f_ei = erwartete Häufigkeit in Kategorie i

Die beobachteten Häufigkeiten können wir direkt ablesen (bzw. beobachten), sie entsprechen den Häufigkeiten, die wir in unserer Stichprobe vorfinden. Für die erwarteten Häufigkeiten wird anhand der theoretischen Verteilung für jede Kategorie die Wahrscheinlichkeit 𝜋_𝑖 bestimmt, eine Beobachtung in dieser Kategorie zu realisieren (𝜋 steht hier für die Wahrscheinlichkeit in der Population, nicht zu verwechseln mit der Kreiszahl 𝜋). Diese Wahrscheinlichkeiten werden in Abhängigkeit der Stichprobengröße in erwartete Häufigkeiten umgerechnet:

f_ei = erwartete Häufigkeit in Kategorie i = 𝜋_𝑖 ⋅ n

Dies klingt komplizierter als es ist. Wenn Sie davon ausgehen, dass das Geschlecht beispielsweise in der Population gleichverteilt ist und Sie eine Stichprobe mit n=100 Personen ziehen, dann lautet die Berechnungsformel für die erwarteten Häufigkeiten in der Kategorie „männlich“:

f_e,männlich = 𝜋_𝑖 ⋅ n = 50% ⋅ 100 = 0,5 ⋅ 100 = 50.

Sie würden also erwarten, dass in Ihrer Stichprobe 50 Männer vorkommen. Um dies nochmal zu verdeutlichen, hier ein weiteres Beispiel.

Beispiel Frauenanteil Burger-Kunden: Schritt 1 Berechnung der Häufigkeiten

Das FiveProfs-Management hat die Vermutung, dass derzeit weniger weibliche Kunden in die Restaurants gehen als bei der Konkurrenz. Um zu prüfen, ob die FiveProfs-Filialen wirklich bei Frauen unbeliebter sind als andere Burger-Filialen, soll nun eine Studie durchgeführt werden, die wir im Folgenden mit dem χ2-Test auswerten. Die Marktforschung hat ergeben, dass bundesweit 60% der Burger-Kunden männlich sind. Nun erheben wir in unseren Filialen eine Stichprobe um herauszufinden, ob sich die Geschlechterverteilung hiervon unterscheidet.

Stichprobengröße einer Befragung in unserer Burgerkette: n = 50

Die Hypothesen lauten:

H0:
Die Geschlechterverteilung unserer Kunden entspricht dem Burgerketten-Durchschnitt von 60/40

H1:
Die Geschlechterverteilung unserer Kunden entspricht nicht dem Burgerketten-Durchschnitt von 60/40

Berechnung der erwarteten Häufigkeiten:

𝜋_weiblich= 0,4 (40%)

𝜋_männlich= 0,6 (60%)

f_e,weiblich = 𝜋_weiblich ⋅ n = 0,4 ⋅ 50 = 20
f_e,männlich = 𝜋_männlich ⋅ n = 0,6 ⋅ 50 = 30

Hieraus werden wir nun im nächsten Schritt den χ2-Wert bestimmen.

Schritt 2: Berechnung des χ²-Werts

Der χ2-Wert soll die Differenz zwischen den beobachteten und den erwarteten Werten wiedergeben. Hierfür berechnen wir also zunächst die Differenz von f_b und f_efür alle Kategorien i. Diese Abweichungen werden aufsummiert, hierbei haben wir jedoch wieder das „Problem“, dass die Summe der Abweichungen zwangsweise 0 ergeben würde (da die Abweichungen in den Kategorien immer in die gegenseitige Richtung vorliegen und per Definition gleich groß sind). Die Lösung: Wir quadrieren die Summe der Abweichungen (wie bei der Berechnung der Varianz). Die quadrierten Abweichungen werden nun noch abschließend an der jeweiligen erwarteten Häufigkeit relativiert. Dies ist wichtig, da eine Abweichung von 10 bei einem erwarteten Wert von 1000 zum Beispiel weniger bedeutsam ist als eine Abweichung von 10 bei einem erwarteten Wert 20. Durch die Relativierung an den erwarteten Häufigkeiten erhalten wir daher ein besser interpretierbares Ergebnis: den χ2-Wert.

Die Formel lautet:

Der resultierende χ2-Wert hat dabei folgende Eigenschaften:

Liegen keine Abweichungen vor so ist χ² = 0
Je größer die Abweichungen, desto größer χ²
χ² kann nur positive Werte annehmen – d.h. es können keine gerichteten Hypothesen getestet werden.

Beispiel Frauenanteil Burger-Kunden: Schritt 2 Berechnung des χ2-Werts

Wir wollen nun die bereits im vorausgegangenen Beispiel berechneten erwarteten und beobachteten Häufigkeiten nutzen um den korrespondierenden χ2-Wert zu berechnen. Unsere Stichprobe von n = 50 Kunden hat folgende beobachteten Häufigkeiten: f_b,weiblich = 12 und f_b,männlich = 38

Die erwarteten Häufigkeiten sind f_e,weiblich = 20 und f_e,männlich = 30 (siehe Box zuvor).

Nun berechnen wir die Abweichung Schritt für Schritt, bzw. Kategorie für Kategorie.

Wir starten mit den weiblichen Kunden:

(f_b,weiblich – f_e,weiblich)² = (12 -20)² = -8²= 64. Dies teilen wir durch f_e,weiblichund erhalten 64/20 = 3,2

Nun kommen die männlichen Kunden:

(f_b,männlich – f_e,männlich)² = (38 -30)² = 8²= 64. Dies teilen wir durch f_e,männlichund erhalten 64/30 = 2,13

Abschließend bilden wir die Summe über alle Kategorien: 3,2 + 2,13 und erhalten den χ2-Wert von 5,33.

Nun haben wir erfolgreich den χ2-Wert errechnet und sehen, dass es Abweichungen zwischen den erwarteten und beobachteten Werten gibt. Doch was genau bedeutet nun ein χ2-Wert von 5,33 ? Hierfür müssen wir im nächsten Schritt diesen Wert, anhand der χ2-Verteilung abhängig von den Freiheitsgraden des Tests, interpretieren.

Schritt 3: Berechnung der Freiheitsgrade

Der χ² Wert folgt einer kontinuierlichen Verteilung, die von der Anzahl der Freiheitsgrade (degrees of freedom oder kurz df) abhängt – die Freiheitsgrade berechnen sich hierbei über k – 1, wobei k die Anzahl der Kategorien ist.

Beispiel Frauenanteil Burger-Kunden: Schritt 3 Berechnung der Freiheitsgrade

Wie viele Freiheitsgrade hat der Test in unserem Beispiel? Hierfür nehmen wir die Anzahl der Kategorien und ziehen 1 ab. Hier haben wir vereinfacht zwei Kategorien: Männer und Frauen.

df = k-1= 2-1 = 1 Wir haben hier 1 Freiheitsgrad vorliegen.

Anmerkung: In einer echten Studie sollten Sie natürlich noch „Divers“ ergänzen und hätte somit 3 Kategorien und df = 3-1 = 2 Freiheitsgrade.

Video 12.4 Chi-Quadrat Anpassungstest | Berechnung des Chi2 Werts

Schritt 4: Berechnung der Prüfgröße χ²_kritund Entscheidung über die Hypothesen

Im Folgenden wollen wir die kritische Prüfgröße festlegen. Dies ist der Wert, ab dem wir nicht mehr daran glauben, dass es sich bei der Abweichung der beobachteten von den erwarteten Werten um einen Zufall handelt. Wo dieser Wert liegt, das hängt zum einen davon ab welches Signifikanzniveau Sie zugrunde legen. Wie bereits im letzten beiden Kapiteln besprochen, kann dies grundsätzlich beliebig von Ihnen festgelegt werden. Übliche Signifikanzniveaus sind jedoch 5% und 1%. Dies bedeutet, dass wir, sofern die Auftretenswahrscheinlichkeit der Abweichung kleiner ist als dieser Prozentwert, die H₀ verwerfen und die H₁ annehmen. In anderen Worten gehen wir ab diesem Wert nicht mehr davon aus, dass diese Abweichung ein Zufall ist, sondern unterstellen, dass es einen tatsächlichen Unterschied zwischen der Stichprobe und der Population gibt. Hierfür müssen wir zunächst das gewählte Signifikanzniveau in eine Prüfgröße umwandeln, also in einen χ² Wert, ab dem wir die Nullhypothese ablehnen. Dieser wird auch kritischer χ² Wert genannt (χ²_krit). Wie beim Z-Test zuvor lässt sich dieser Wert durch die Berechnung der Fläche unter der χ²Verteilung berechnen, indem wir z.B. exakt 5% Fläche abschneiden. Bei der χ² Verteilung ist das insofern noch etwas einfacher, als dass diese immer positiv ist und wir die Fläche somit nicht auf beide Enden der Verteilung aufteilen müssen. Diese kritische Fläche (Ablehnungsbereich) liegt immer rechts. Jedoch müssen wir hierbei einen weiteren Schritt beachten. Da der Verlauf der χ² Verteilung von den Freiheitsgraden abhängt, ändert sich diese Fläche auch mit den Freiheitsgraden, die vorliegen. Daher müssen wir nun in einer entsprechenden χ² Tabelle den kritischen Wert (Prüfgröße) unter Anbetracht der vorliegenden Freiheitsgrade und des gewählten Signifikanzniveaus bestimmen. Haben wir dies gemacht gilt:

Falls χ²_empirisch> χ²_kritisch wird die H₀ verworfen und die H₁ angenommen und Sie können sagen, dass es äußerst unwahrscheinlich ist, dass die Stichprobe aus der Population mit der unterstellten Verteilung stammt. Ist dies nicht der Fall, so gehen Sie weiterhin davon aus, dass es sich um eine (Zufalls-) Stichprobe aus der Population mit der unterstellten Verteilung handelt (H₀wird beibehalten, muss aber nicht zwangsläufig richtig sein).

Wie auch beim Z-Test können Sie alternativ auch die Wahrscheinlichkeit p(χ²_emp) mit dem Signifikanzniveau 𝛼 vergleichen. Hierzu rechnen Sie Ihren vorliegenden χ² Wert (χ²_empirisch) über die Tabelle in einen p-Wert um (p_empirisch) und vergleichen diesen mit Ihrem kritischen p-Wert (entspricht dem Signifikanzniveau, also z.B. 5%). Der empirische p-Wert gibt hierbei die Wahrscheinlichkeit an, solche Daten zu finden unter Annahme der H₀, also dass es keinen Unterschied zwischen Stichprobe und Population gibt. Hierbei gilt: Falls p_{empirisch <} p_kritisch wird die H₀ verworfen und die H₁ angenommen.

Ob Sie die Prüfgröße χ²_empirischinterpretieren oder den p-Wert, bleibt dabei ganz Ihnen überlassen. In der Praxis ist es oft einfach den p-Wert zu interpretieren, da Sie hierfür keine Verteilungstabelle benötigen. Hierbei reicht es, das Signifikanzniveau 𝛼 festzulegen und Sie können direkt entscheiden, ob die H₀ verworfen werden kann.

Beispiel Frauenanteil Burger-Kunden: Schritt 4 Berechnung der Prüfgröße und Entscheidung

Im nächsten Schritt vergleichen wir den empirisch gefundenen χ2-Wert von 5,33, mit der Prüfgröße. Diese können wir aus einer Tabelle der χ2-Verteilung ablesen, wenn das Signifikanzniveau und die Freiheitsgrade bekannt sind. Wir gehen im Folgenden davon aus, dass wir auf dem 5%-Niveau testen (𝛼 = 0,05) und haben, wie in der Box zuvor berechnet einen Freiheitsgrad.

Daraus können wir den kritischen χ2-Wert von 3,84 ablesen (z.B. hier, erste Zeile, vierter Wert von rechts).

Da χ²_empirisch> χ²_kritisch (5,33 > 3,84) wird die H₀ verworfen und die H₁ angenommen.

Dies bedeutet, dass die Geschlechterverteilung in der neuen Filiale nicht unserem Burgerketten-Durchschnitt von 60/40 entspricht. Unsere Kunden weichen also im Hinblick auf das Geschlecht signifikant von den normalen Burgerkunden ab.

Wir könnten aus der Tabelle auch die Wahrscheinlichkeit für die empirisch gefundene Abweichung ermitteln. Da die Tabelle nur bestimmte Wahrscheinlichkeiten darstellt, geht dies mit der Tabelle nicht ganz exakt. Mit einem Statistikprogramm bekommen Sie jedoch automatisch den exakten p-Wert ausgegeben.

Aus der Tabelle können wir in der ersten Zeile ablesen, dass der zugehörige p-Wert zu einem χ²-Wert von 5,33 über 0,975 liegt. Da hier immer die Gegenwahrscheinlichkeit abgelesen wird, müssen wir hierbei noch 1 – 0,975 rechnen und können damit sagen, dass der zugehörige p-Wert unter 0,025 bzw. unter 2,5% liegt. Die Wahrscheinlichkeit dafür, dass die Abweichung der Geschlechterverteilung in unserer Stichprobe nur ein Zufall ist, liegt also bei unter 2,5%.

Expertenwissen: Effektstärke

Das zugehörige Maß für die Effektstärke ist ω² bzw. der Phi-Koeffizient

Video 12.5 Chi-Quadrat Anpassungstest | Interpretation

Im folgenden Video gibt es noch ein weiteres Rechenbeispiel zum Chi-Quadrat Anpassungstest.

Video 12.6 Chi-Quadrat Anpassungstest | Rechenbeispiel

12.5 Der Chi-Quadrat Unabhängigkeitstest

Eine weitere Variante des Chi-Quadrat-Tests ist der sogenannte Chi-Quadrat Unabhängigkeitstest, mit dem wir uns nun im Folgenden beschäftigen. Der Chi-Quadrat Unabhängigkeitstest beschäftigt sich immer mit genau zwei nominal skalierten Variablen und der Frage, ob diese unabhängig voneinander sind oder ob es einen irgendwie gearteten Zusammenhang zwischen den Variablen gibt. Ein Beispiel könnte das Rauchverhalten (ja/nein) sein und die Frage, ob dieses vom Geschlecht (männlich/weiblich) abhängig ist.

Haben, wie in diesem Beispiel, beide Variablen genau zwei Ausprägungen (dichotome Variablen), dann spricht man auch von einem sogenannten Vier-Felder-Test. Hat eine der Variablen, oder beide, mehr als zwei Ausprägungen, so spricht man allgemein vom Mehrfelder-Test.

Auch bei dieser Variante des Chi-Quadrat-Tests sind die Hypothesen formal festgelegt und lauten:

H₀: Die beiden Variablen sind voneinander stochastisch unabhängig.
H₁: Es gibt einen irgendwie gearteten Zusammenhang zwischen den Merkmalsausprägungen der einen Variable und der Ausprägungen der anderen.

Dabei gilt auch bei dieser Variante, dass der Chi-Quadrat-Test grundsätzlich nur ungerichtete Hypothesen testen kann. Dies soll das folgende Beispiel nochmal verdeutlichen.

Beispiel Hypothesen Chi-Quadrat Unabhängigkeitstest

Wenn wir prüfen wollen ob die Variablen Schulabschluss (Abitur/Realschule/Hauptschule) und Rauchen (ja/nein) unabhängig voneinander sind

H₀: Es gibt keinen Zusammenhang zwischen dem Schulabschluss und dem Rauchverhalten (die Variablen sind unabhängig)
H₁: Es gibt einen irgendwie gearteten Zusammenhang zwischen dem Schulabschluss und dem Rauchverhalten

Video 12.7 Chi-Quadrat Unabhängigkeitstest | Bildung der Hypothesen

Wenn wir die H₁ aus dem obigen Beispiel betrachten, so können wir als Ergebnis eines solchen Chi-Quadrat Test zum Beispiel sagen, dass sich die Schulabgänger in ihrem Raucher-Anteil grundsätzlich unterscheiden (falls der Test signifikant wird und wir die H₀ verwerfen können). Wir wissen aber nicht wer besonders viel raucht. Daher ist es sinnvoll, zunächst die sogenannte Kreuztabelle zu betrachten. Die Kreuztabelle (auch Kontingenztabelle oder Kontingenztafel) ist eine Möglichkeit zur Darstellung der gemeinsamen Verteilung von zwei kategorialen oder kategorisierten Merkmalen. Um deskriptiv zu prüfen, ob es einen Zusammenhang gibt, kann man hierbei die relativen Häufigkeiten berechnen (dies haben wir in Kapitel 3 besprochen). Die Kreuztabelle ist gleichzeitig auch die Grundlage um in diesem Fall die erwarteten Häufigkeiten und damit die Prüfgröße χ²_empirisch zu errechnen. Hierbei geht man wie folgt vor.

Schritt 1: Berechnung der Randhäufigkeiten

Randhäufigkeiten geben an, wie häufig bestimmte Ausprägungen eines Merkmals vorkommen – unabhängig von den Ausprägungen des anderen Merkmals. Die Randhäufigkeiten ergeben sich durch einfaches Aufsummieren der absoluten Häufigkeiten in jeder Zeile und jeder Spalte. Die folgende Kreuztabelle zeigt das Ergebnis einer Befragung. Hierbei wurden Schüler und Studenten, Berufstätige und Rentner befragt, ob sie einer neue Smart-Phone-Bestellmöglichkeit in unseren Filialen nutzen würden (Ja / Nein). Die Randhäufigkeiten sind rot eingetragen und der Wert rechts unten entspricht der Stichprobengröße n=200.

	Schüler & Studenten	Berufs- tätige	Rentner
J	28	16	6	50
N	32	64	54	150
	60	80	60	200

Schritt 2: Bestimmung der relativen Randhäufigkeiten

Im nächsten Schritt bestimmen wir die relativen Randhäufigkeiten, indem wir die absoluten Randhäufigkeiten an der Stichprobengröße (n=200) relativieren. Die relativen Randhäufigkeiten geben an, wie häufig ein Merkmal in der Stichprobe vorkommt. In der folgenden Tabelle sind die relativen Randhäufigkeiten rot dargestellt. Hieraus können wir beispielsweise ablesen, dass insgesamt 25% der Stichprobe gerne die neue Smartphone-Bestellmöglichkeit nutzen würden.

	Schüler & Studenten	Berufs- tätige	Rentner
J	28	16	6	0,25
N	32	64	54	0,75
	0,3	0,4	0,3	1,00

Schritt 3: Bestimmung der relativen erwarteten Häufigkeiten je Zelle

Aus den relativen Randhäufigkeiten können wir nun die erwarteten Häufigkeiten je Zelle ermitteln, denn bei stochastischer Unabhängigkeit ist die Wahrscheinlichkeit für das gemeinsame Auftreten zweier Ereignisse, gleich dem Produkt ihrer Wahrscheinlichkeiten. Anders ausgedrückt: Sind die Variablen tatsächlich komplett unabhängig (H₀) dann sollte sich die relative Häufigkeit jeder Zelle dadurch ergeben, dass ich die relative Häufigkeit der beiden zugehörigen Merkmale multipliziere. Wenn, wie in unserem Beispiel, in Summe 25% der neuen Zahlmethode zustimmen, so sollte die relative Häufigkeit für die Gruppe Schüler & Studenten 0,25 ⋅ 0,3 = 0,075 entsprechen (Auftretenswahrscheinlichkeit „Zustimmung“ multipliziert mit Auftretenswahrscheinlichkeit „Schüler & Studenten“). Wir können nun also sagen, dass aus der multiplikativen Verknüpfung der Randhäufigkeiten die erwarteten Häufigkeiten f_eij, unter der Annahme der Unabhängigkeit als Nullhypothese H₀, abgeleitet werden können. Der Index i steht hierbei für die Kategorien der ersten Variable, der Index j für die Kategorien der zweiten Variable. Die relativen erwarteten Häufigkeiten sind in der folgenden Tabelle orange dargestellt. Tipp: Alle relativen erwarteten Häufigkeiten sollten zusammengezählt 1 ergeben.

	Schüler & Studenten	Berufs- tätige	Rentner
J	28 0,075	16 0,1	6 0,075	0,25
N	32 0,225	64 0,3	54 0,225	0,75
	0,3	0,4	0,3	1,00

Schritt 4: Bestimmung der absoluten erwarteten Häufigkeiten je Zelle

Um nun die erwarteten Häufigkeiten mit den beobachteten Häufigkeiten vergleichen zu können müssen wir abschließend die relativen Häufigkeiten noch in absolute Häufigkeiten umrechnen. Hierzu multiplizieren wir einfach alle Werte mit der Stichprobengröße n. Die absoluten erwarteten Häufigkeiten sind in der folgenden Tabelle grün dargestellt.

	Schüler & Studenten	Berufs- tätige	Rentner
J	28 15	16 20	6 15	0,25
N	32 45	64 60	54 45	0,75
	0,3	0,4	0,3	1.00

Nun können wir schon rein deskriptiv einen Unterschied zwischen den beobachteten und den erwarteten Werten feststellen. Um nun aber sagen zu können, wie groß die Abweichung in Summe ist und wie wahrscheinlich eine solch große Abweichung unter Annahme der H₀ ist, müssen wir die Prüfgröße Chi-Quadrat berechnen.

Schritt 5: Berechnung der Prüfgröße χ²_empirischund Entscheidung über die Hypothesen

Die Prüfgröße χ²_empirischfür diesen Test berechnet sich dabei sehr ähnlich, wie beim Chi-Quadrat Anpassungstest. Der einzige Unterschied ist, dass wir nun sowohl über die Zeilen als auch über die Spalten aufsummieren (also die Abweichung aller Zellen der Kreuztabelle berechnen). Daher benötigen wir zwei Summenzeichen und die zwei Indizes i und j.

Berechnung des χ²-Werts für unser Beispiel

Für die Berechnung des χ²-Werts wird für jede Zelle die quadrierte Differenz zwischen beobachtetem und erwartetem Wert berechnet und jeweils an dem erwarteten Wert relativiert. Dies kann zunächst Zeilenweise oder Spaltenweise (wie unten) erfolgen. Am Ende werden alle Werte (hier alle 6 Zellen) aufsummiert.

In unserem Beispiel ergibt die Berechnung einen χ²-Wert von ca. 23,3. Diesen Wert werden wir im Folgenden interpretieren.

Video 12.8 Chi-Quadrat Unabhängigkeitstest | Berechnung des Chi2 Werts

Zur Interpretation des χ²-Werts benötigen wir auch beim Unabhängigkeitstest zunächst die Freiheitsgrade. Diese berechnen sich beim Chi-Quadrat Unabhängigkeitstest über df = (k-1)⋅(l-1), wobei k die Anzahl der Kategorien des Merkmals A ist und l die Anzahl der Kategorien des Merkmals B. Für unser Beispiel wäre dies also df= (3-1) ⋅ (2-1) = 2. Über die Freiheitsgrade und das selbst festgelegt Signifikanzniveau lässt sich nun wieder die kritische Prüfgröße χ²_kritischermitteln. Bei einem Signifikanzniveau von α= 5% wäre dies der aus der Tabelle abgelesene Wert χ²_kritisch =5,99.

Der berechnete χ²_empirischliegt mit 23,3 sehr deutlich über dem kritischen Wert. Auch hier gilt falls χ²_empirisch> χ²_kritisch wird die H₀ verworfen und die H₁ angenommen. Konkret auf dieses Beispiel angewendet können wir also nun sagen, dass es einen signifikanten Unterschied zwischen den Gruppen Schüler/Student, Angestellte und Rentner gibt, im Hinblick auf die Akzeptanz der neuen Smartphone-Bestellmöglichkeit. Mehr kann der Test selbst erstmal nicht aussagen. Um nun zu verstehen, welche Gruppe eine besonders hohe Affinität für diese neue Technologie hat, müsste man die einzelnen Spalten in Form von Spalten-Prozenten vergleichen. Die Darstellung der Spaltenprozente ermöglicht hierbei einen sehr schnellen Überblick über die deskriptive Verteilung in den 3 Gruppen. Hierbei wird schnell deutlich, dass die neue Smartphone-Bestellfunktion nur bei Schülern mit 47% einen guten Anklang findet. Bei Berufstätigen und Rentnern ist diese neue Technologie mit nur 20% bzw. 10% Zustimmung nicht gefragt.

	Schüler & Studenten	Berufs- tätige	Rentner
J	47%	20%	10%
N	53%	80%	90%

Der Chi-Quadrat-Test gibt uns nun nur die Information, dass die Unterschiede zwischen allen 3 Gruppen in Summe signifikant sind, nicht aber zwischen welchen Gruppen-Paaren signifikante Unterschiede bestehen. Wir wissen somit z.B. nicht, ob der Unterschied zwischen Berufstätigen und Rentner signifikant ist. Um dies herauszufinden, könnte man die Daten aufsplitten und mehrere Vierfelder-Tests durchführen. In diesem Beispiel wären 3 solche Tests notwendig, für jede mögliche Paarkombination eine.

Video 12.9 Chi-Quadrat-Unabhängigkeitstest | Interpretation des Tests

12.6 Voraussetzungen für den Chi-Quadrat Test

Beide Arten des Chi-Quadrat Tests haben als nicht-parametrischer Test nur wenig Voraussetzungen, die vorab erfüllt werden müssen. Grundsätzlich geht auch die Chi-Quadratverteilung von Zufallsvariablen aus, daher sollte es sich um eine Zufallsstichprobe handeln. Beim Chi-Quadrat Unabhängigkeitstest sollten die Messungen voneinander unabhängig sein. Dies bedeutet, dass der Test nicht geeignet ist für Messwiederholungsdesigns bzw. Within-subjects Designs, bei denen z.B. dieselben Personen mehrmals befragt werden.

Es handelt sich bei den Chi-Quadrat-Tests um sogenannte asymptotische Tests, d.h. die Kennwerteverteilung approximiert nur eine χ²-Verteilung, folgt dieser aber nie exakt. Daher gilt: je größer die Stichprobe ist, desto besser kann die Testverteilung mit einer χ²-Verteilung approximiert werden. Die Stichprobe sollte daher nicht zu klein sein. Eine übliche Faustregel besagt, dass die erwarteten Häufigkeiten in jeder Kategorie zumindest 5 betragen (sonst büßt der Test Teststärke ein). Lösung bei kleinen Stichproben: Exakter Test nach Fisher (1922), dieser ist in SPSS verfügbar.

12.7 Chi-Quadrat Anpassungstest in SPSS berechnen

Auch wenn es relativ leicht möglich ist den Chi-Quadrat Anpassungstest von Hand zu berechnen, so können wir natürlich hierfür auch SPSS zur Hilfe nehmen. Die Voraussetzung hierfür ist jedoch, dass die Rohdaten zur Verfügung stehen. Es reicht also nicht wenn Sie z.B. wissen, dass es 550 Männer und 450 Frauen in einer Stichprobe vorhanden sind, sondern Sie benötigen den kompletten Datensatz mit 1.000 Einträgen um den Test in SPSS berechnen zu können (Tipp: In R können Sie den Test auch nur mit den Häufigkeiten berechnen). Das Menü zur Berechnung des Test ist gut versteckt. Sie müssen zunächst auf „Nicht parametrische Test“ klicken, denn der Chi-Quadrat Test verwendet nominale (also nicht metrisch-skalierte) Daten. Im nächsten Schritt werden Ihnen verschiedene Assistenten angeboten. Da Sie jedoch schon wissen welchen Test Sie durchführen wollen können Sie mit einem Klick auf „Klassische Dialogfelder“ direkt zur Auswahl des „Chi-Quadrat-Tests“ wechseln. Hier der ganze Pfad:

Analysieren > Nicht parametrische Tests > Klassische Dialogfelder > Chi-Quadrat-Test.

Die Vorgehensweise und Interpretation des Chi-Quadrat Anpassungstests wird im folgenden Video erläutert.

Video 12.10 Chi-Quadrat Anpassungstest in SPSS berechnen

12.8 Chi-Quadrat Unabhängigkeitstest in SPSS berechnen

Auch der Chi-Quadrat Unabhängigkeitstest lässt sich sehr einfach in SPSS berechnen. Der Test ist über das Menü zu „Kreuztabellen“ erreichbar welches wir schon besprochen haben:

Analysieren > Deskriptive Statistiken > Kreuztabellen

Zusätzlich zur Erstellung der Kreuztabelle können Sie den Chi-Quadrat-Test über den Button „Statistiken„ auswählen. Dies wird im nächsten Video im Detail an einem Beispiel besprochen.

Video 12.11 Chi-Quadrat Unabhängigkeitstest in SPSS berechnen

12.9 Übungsfragen

Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!

In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!

12.10 Übungsaufgaben

Übungsaufgabe Chi-Quadrat-Anpassungstest

Wir wollen herausfinden ob sich die Burger-Kunden unserer Five-Profs Filialen hinsichtlich ihrer Bildung von der Population unterschieden. Hierzu betrachten wir das Merkmal Akademiker / Nicht-Akademiker. Wir haben durch eine kurze Recherche herausgefunden das in Deutschland 35% der Personen zwischen 25 und 65 Jahren einen akademischen Abschluss haben. Wir haben daraufhin eine Befragung von N=465 Burgerkunden zwischen 25 und 65 Jahren durchgeführt, bei der insgesamt 186 Personen angaben, einen akademischen Abschluss zu haben.Zu welchem Ergebnis kommen Sie?

Eine Lösung finden Sie Schritt für Schritt erklärt im folgendem Video:

Übungsaufgabe Chi-Quadrat-Unabhängigkeitstest

Leider bekommen wir vermehrt Beschwerden über auf der Straße entsorgten Müll von Anwohnern rund um die FIVE PROFs Burger-Filialen. Wir vermuten, dass dies vor allem dann auftritt wenn die Filiale einen Drive-In hat und die Kunden unserer Burger direkt im Auto essen. Um diese zu prüfen führen wir einen Chi-Quadrat-Unabhängigkeitstest durch mit den Variablen Drive-In (JA/Nein) und Beschwerde über Müll eingegangen (Ja/Nein). Wir haben hierzu 40 Filialen ausgewählt, wovon 20 einen Drive-In haben und 20 nicht. Unten sehen Sie die resultierende Tabelle:

Filialen	Keine Beschwerde über Müll aufgetreten	Beschwerde über Müll aufgetreten	Gesamt
Mit Drive-In	13	7	20
Ohne Drive-In	15	5	20
Gesamt	28	12	40

Gibt es einen statistisch signifikanten Zusammenhang zwischen Drive-In und den Beschwerden über Müll?