Inferenzstatistik
9 Konfidenzintervalle
9.0 Einführung
Wie im letzten Kapital bereits erwähnt, gibt es in der Inferenzstatistik zwei Verfahren, mit deren Hilfe wir aus einer gezogenen Stichprobe die entsprechenden Populationsparameter schätzen können. Diese sind:
- Die Punktschätzung
- Die Intervallschätzung.
Die Punktschätzung schätzt anhand eines erwartungstreuen Stichprobenkennwerts einen einzelnen, möglichst genauen Näherungswert für den gesuchten Populationsparameter. Diese punktgenaue Schätzung trifft jedoch nur sehr selten den tatsächlichen Populationsparameter. In diesem Kapitel widmen wir uns nun dem zweiten und in der Wissenschaft auch beliebteren Verfahren, der Intervallschätzung. Diese gibt einen Bereich vor, in dem der gesuchte Populationsparameter wahrscheinlich liegt.
Beispiel Punkt- und Intervallschätzung
Wir wollen herausfinden, wie alt die Kunden unserer Burger-Kette sind. Hierfür nutzen wir zwei unterschiedliche Verfahren der Parameterschätzung und erhalten entsprechend unterschiedliche Ergebnisse.
- Mögliches Ergebnis der Punktschätzung: Unsere Kunden haben ein Durchschnittsalter von 26,5 Jahren, der Standardfehler des Schätzers liegt bei 0,75
- Mögliches Ergebnis der Intervallschätzung: Wir sind uns sehr sicher (üblicherweise zu 95%), dass das Durchschnittsalter der Kunden zwischen 25,03 und 27,97 Jahren liegt.
Die Punktschätzung ist dabei vergleichbar mit dem Versuch, mit einem Dartpfeil eine Fliege zu treffen. Das wird nie klappen, aber das Ziel ist es möglichst nahe dran zu sein (wie nahe, das sagt uns der Schätzfehler). Die Intervallschätzung entspricht der üblicheren Methode der Fliegenklatsche, welche eine deutlich höhere Trefferquote hat. Wir müssen hierfür nämlich nicht wissen, wo genau die Fliege ist, es reicht zu wissen, in welchem Bereich sie sich wahrscheinlich aufhält.
9.1 Intervallschätzung
Die Intervallschätzung schätzt auf Basis einer Zufallsstichprobe einen Bereich (ein Intervall), in dem der gesuchte Populationsparameter mit einer festgelegten Wahrscheinlichkeit liegt. Dieser Bereich wird auch Konfidenzintervall oder Vertrauensintervall genannt.
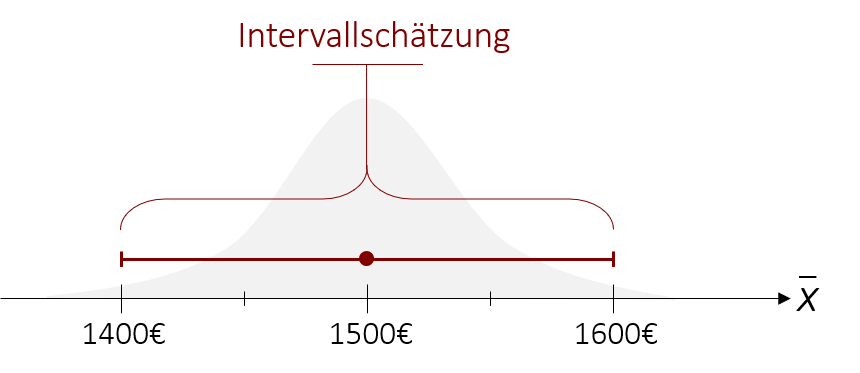
Im Gegensatz zur Punktschätzung ist das Ziel des Verfahrens also, keinen bestimmten Punkt anzugeben, sondern einen Bereich zu bestimmen, in dem der Parameter mit einer Wahrscheinlichkeit von z.B. 95% liegt. Wenn wir beispielsweise das durchschnittliche Einkommen schätzen möchten, so würden wir bei der Punktschätzung den Mittelwert der Stichprobe von = 1500€ als Schätzung für den Populationsmittelwert nennen. Bei der Intervallschätzung hingegen geben wir einen Bereich an und können somit die Aussage tätigen, dass der Populationsmittelwert mit einer Wahrscheinlichkeit von 95% zwischen 1400€ und 1600€ liegt.
Um solch ein Konfidenzintervall zu konstruieren, benötigen wir zunächst eine erwartungstreue Punktschätzung, wie beispielsweise den Stichprobenmittelwert, der uns als Ausgangspunkt für unsere Schätzung dient.
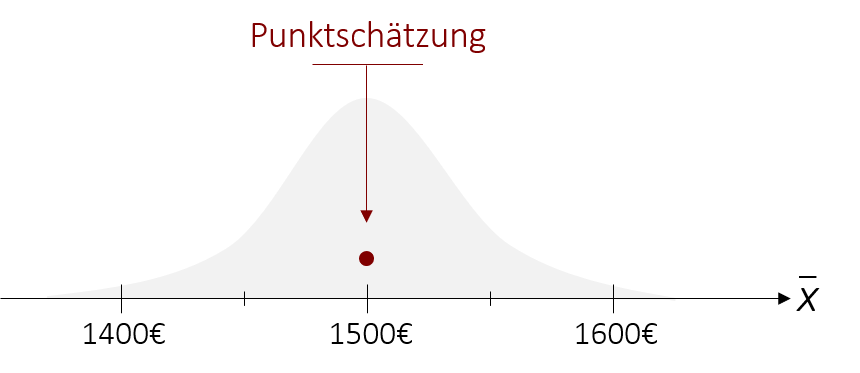
Im nächsten Schritt wird um diesen Punkt herum ein (symmetrisches) Intervall bestimmt. Wie groß dieses Intervall ist, hängt dabei von der Wahrscheinlichkeit ab, die wir selbst im Vorhinein definieren. Wenn wir uns beispielsweise sehr sicher sein wollen, dass unser gesuchter Parameter wirklich in dem Intervall liegt, könnten wir auch das 99%-Konfidenzintervall konstruieren. Dies bedeutet, dass der wahre Wert mit einer Wahrscheinlichkeit von 99% in diesem Bereich liegt, hätte aber auch zur Folge, dass das Intervall dadurch größer wird (dazu später mehr).
Das folgende Video von Five Profs zeigt Ihnen das Konzept der Konfidenzintervalle an einem Beispiel.
9.1 Konfidenzintervall | Einführung
Um nun zu definieren wie groß unser Konfidenzintervall ist beziehungsweise wo seine „Grenzen“ liegen, müssen wir jedoch nicht nur die Wahrscheinlichkeit im Vorhinein bestimmen, sondern auch wissen, wie wir aus dieser Wahrscheinlichkeit einen Wertebereich bestimmen können. Machen wir hierzu zunächst einen kleinen Exkurs in die Welt der Wahrscheinlichkeitsverteilungen.
9.2 Exkurs Wahrscheinlichkeitsverteilungen
Wahrscheinlichkeitsverteilungen bilden die Auftrittswahrscheinlichkeit (auf der y-Achse) für unterschiedliche Merkmalsausprägungen (auf der x-Achse) ab. Die einzelnen Wahrscheinlichkeiten werden dabei als Zahlen zwischen 0 und 1 angegeben. So wird eine 50% Wahrscheinlichkeit für das Ereignis A als P(A)= 0,5 beschrieben. Wenn man alle Wahrscheinlichkeiten zusammenrechnet, ergeben diese zusammen 1 (=100%).
Man unterscheidet hierbei grundsätzlich zwischen diskreten und stetigen Wahrscheinlichkeitsverteilungen.
Diskrete Wahrscheinlichkeitsverteilungen
Diskrete Wahrscheinlichkeitsverteilungen ordnen diskreten Zufallsvariablen Auftrittswahrscheinlichkeiten zu. Diese Variablen können nur eine endliche oder abzählbare Menge an Ausprägungen annehmen.
Beispiele für diskrete Wahrscheinlichkeitsverteilungen:
- Ergebnisse beim Münzwurf oder Würfeln
- Geschlecht oder Haarfarbe eines Kindes
- Bestehen / Nicht-Bestehen der Statistik-Klausur
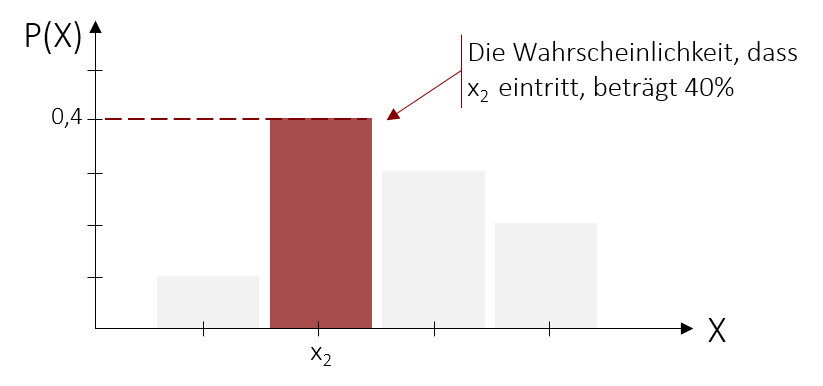
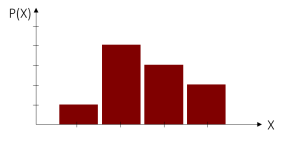
Um nun die Auftrittswahrscheinlichkeit einer einzelnen Merkmalsausprägung (wie z.B. x2) zu bestimmen, müssen wir lediglich den Wert an der entsprechenden Stelle der y-Achse in der Wahrscheinlichkeitsfunktion ablesen. So kann für jede Ausprägung eine Auftrittswahrscheinlichkeit bestimmt werden. Die Wahrscheinlichkeit aller Ausprägungen zusammen beträgt immer 100% oder 1. Grafisch betrachtet haben alle Balken zusammen eine Höhe von 1.
Stetige Wahrscheinlichkeitsverteilungen
Stetige Wahrscheinlichkeitsverteilungen hingegen bilden die Auftrittswahrscheinlichkeit von stetigen Zufallsvariablen ab, welche unendlich viele Merkmalsausprägungen besitzen.
Beispiele für stetige Wahrscheinlichkeitsverteilungen:
- Weite beim Kugelstoßen oder Zeit beim Marathon
- Gewicht von Kühen oder Größe von Bäumen
- Zeit die Studierende auf YouTube verbringen
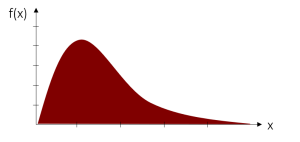
Solch eine Wahrscheinlichkeitsverteilung kann beispielsweise in einer Dichtefunktion abgebildet werden. Sie ist das Äquivalent zur Wahrscheinlichkeitsfunktion bei diskreten Merkmalen und zeigt mittels einer Kurve an, wo sich die Werte der Zufallsvariable am „dichtesten“ scharen.
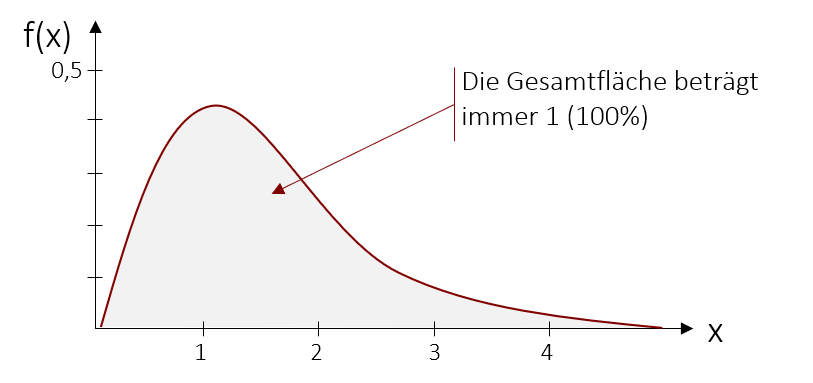
Anders als bei diskreten Merkmalen lässt sich bei stetigen Wahrscheinlichkeitsverteilungen die Auftrittswahrscheinlichkeit einer bestimmten Merkmalsausprägung nicht bestimmen. Die Wahrscheinlichkeit für eine einzelne Ausprägung läuft statistisch gesehen gegen Null, da es unendlich viele andere mögliche Merkmalsausprägungen gibt und alle Möglichkeiten zusammen 1 bzw. 100% ergeben müssen. Man kann jedoch die Auftrittswahrscheinlichkeiten für einen Bereich von Ausprägungen bestimmen. Hierzu berechnen wir ein Integral (=Fläche unter der Dichtefunktion) zwischen zwei Punkten und erhalten somit die Wahrscheinlichkeit für diesen Wertebereich. Die Berechnung von Integralen selbst wird hier in Statistik Grundlagen nicht behandelt und ist auch für die weiteren Verfahren nicht notwendig, da wir uns in der Statistik üblicherweise mit Tabellen behelfen, dazu aber später mehr.
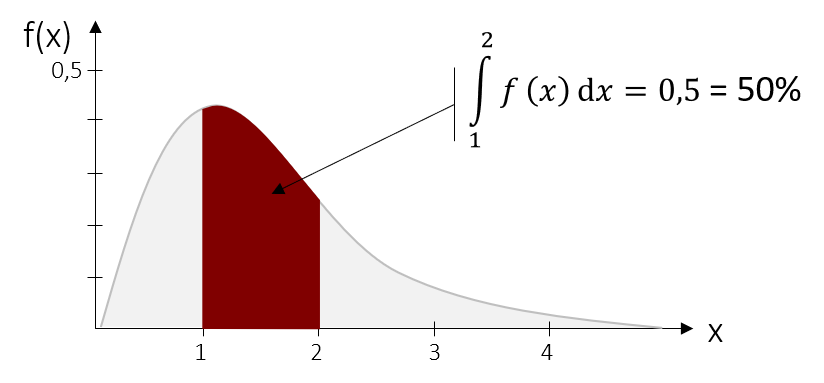
Beispiel Dichtefunktion und Netflix
Die folgende Dichteverteilung zeigt den Netflix Konsum von Studierenden pro Tag (X-Achse). Aus dieser Grafik lässt sich nun die Wahrscheinlichkeit für bestimmte Bereiche ablesen. Beispielsweise beträgt die Fläche zwischen 1 und 2 in der unteren Grafik =0,5 (Wie dieses Fläche berechnet wird, spielt an dieser Stelle zunächst noch keine Rolle). Wir können somit sagen, dass mit einer Wahrscheinlichkeit von 50% ein Wert im Bereich zwischen 1 und 2 auftritt. Anders ausgedrückt, bedeutet dies, dass ein zufällig ausgewählter Studierender mit einer Wahrscheinlichkeit von 50% zwischen einer und zwei Stunden Netflix am Tag schaut. Dies ist natürlich nur ein rein fiktives Beispiel…
Die folgende Tabelle zeigt Ihnen eine Übersicht über die zwei verschiedenen Wahrscheinlichkeitsverteilung und worin sie sich unterscheiden:
| Diskrete Wahrscheinlichkeits-Verteilung | Stetige Wahrscheinlichkeits-Verteilung |
| Endliche Anzahl an Merkmalsausprägungen | Unendliche Anzahl an Merkmalsausprägungen |
 |
 |
| Für jede Ausprägung kann eine Auftritts-Wahrscheinlichkeit exakt bestimmt werden. | Wahrscheinlichkeit einzelner Ausprägungen lässt sich nicht exakt bestimmen. |
| Wahrscheinlichkeit für einen Wertebereich lässt sich durch Addition der einzelnen Auftritts-Wahrscheinlichkeiten bestimmen. | Wahrscheinlichkeit für Bereiche von Ausprägungen lässt sich durch Integrale (=Fläche unter der Dichtefunktion) bestimmen. |
Im Folgenden werden wir uns mit stetigen Wahrscheinlichkeitsverteilungen beschäftigen. Eine der wichtigsten stetigen Verteilungsfunktionen ist die Normalverteilung. Sie kommt in der Natur besonders häufig vor und ist Grundlage für die Inferenzstatistik, weshalb eine kurze Wiederholung an dieser Stelle nicht schadet. Die Einleitung zur Normalverteilung findet sich im Kapitel 2.
Die Normalverteilung
Die Normalverteilung besitzt eine zentrale Bedeutung für die nachfolgenden Schätz- und Testverfahren in der Inferenzstatistik. Oft wird sie auch als Gauß-Kurve oder Gaußsche Glockenkurve bezeichnet. Ihre glockenförmige Form muss dabei keineswegs immer gleich aussehen. Der Verlauf wird durch die beiden Parameter µ (Mittelwert) und σ (Standardabweichung) eindeutig bestimmt. Dadurch variiert die Normalverteilung in ihrer Form abhängig von diesen beiden Werten. Was jedoch gleich bleibt, ist ihre Symmetrie, sodass der Mittelwert, Modus und Median immer auf denselben Wert zusammenfallen.
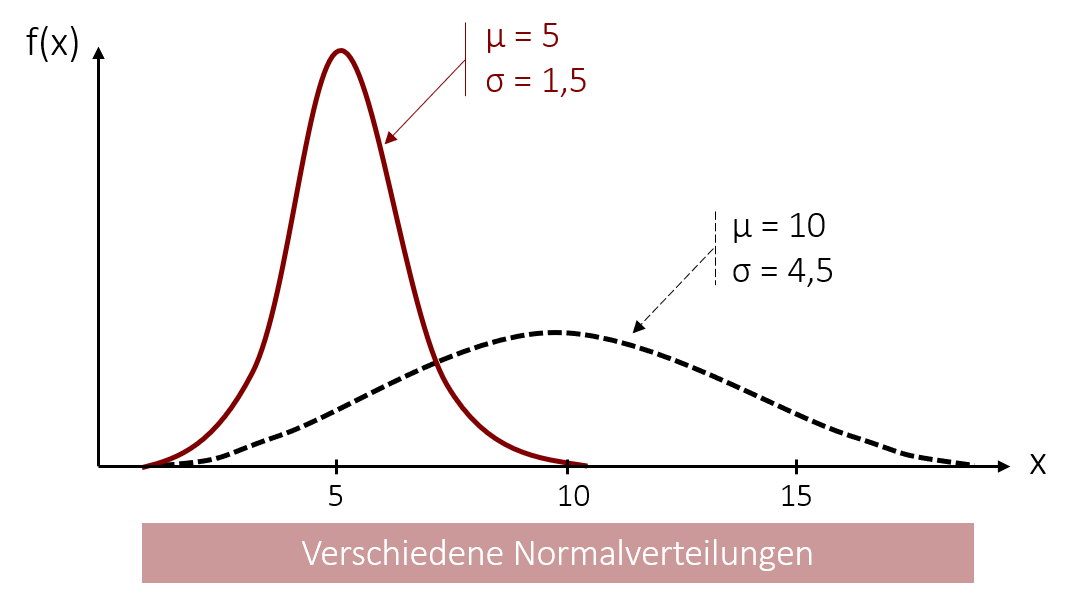
Die Normalverteilung kann nicht nur graphisch veranschaulicht werden, sondern auch in einer Dichtefunktion ausgedrückt werden. Diese Funktion beschreibt eine Schar von Verteilungen, die sich hinsichtlich µ und σ unterscheiden. Wie bei allen stetigen Verteilungen kann man bei der Normalverteilung die Auftrittswahrscheinlichkeit für einen Wertebereich bestimmen. Um zu ermitteln, mit welcher Wahrscheinlichkeit die Werte innerhalb eines bestimmten Bereichs eintreten, berechnet man normalerweise Integrale (=die Fläche unter der Dichtefunktion). Die Dichtefunktion für die Normalverteilung lautet:
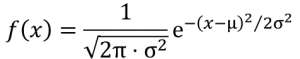
Doch keine Sorge, diese Formel werden Sie nicht brauchen um Inferenzstatistik zu betreiben. Denn bei der Normalverteilung sind, im Gegensatz zu anderen unbestimmten stetigen Verteilungen, die Wahrscheinlichkeiten, mit denen die Werte in bestimmten Intervallen auftreten, immer gleich. Dies vereinfacht die Berechnung von Wahrscheinlichkeiten für Intervalle erheblich. Beispielsweise liegen zwischen den zwei Wendepunkten der Normalverteilung (also μ ± σ) immer ca. 68,27% der Werte.
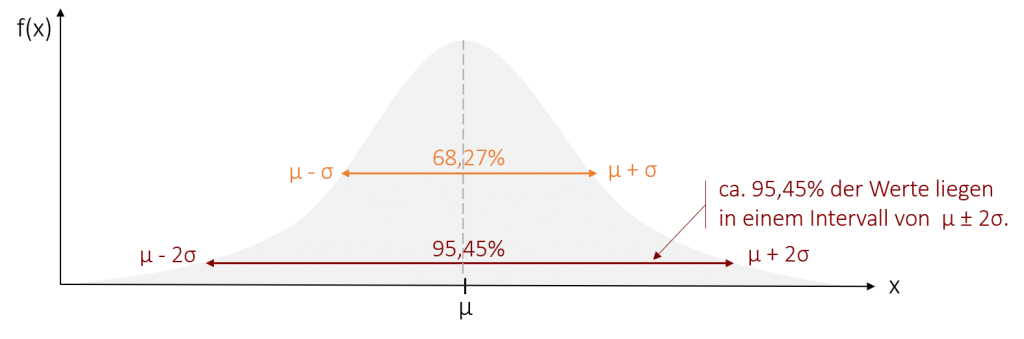
Um die Wahrscheinlichkeitsberechnung noch einfacher zu machen, können wir die Normalverteilung durch eine z-Standardisierung in eine Standardnormalverteilung transformieren. Dies kann man mit jeder Normalverteilung (aber auch nur einer solchen!) durchführen. Dadurch erhalten wir eine immer gleiche Verteilung mit dem Mittelwert µ = 0 und der Standardabweichung σ = 1. Ebenso wie bei der Normalverteilung ist es bei der Standardnormalverteilung festgelegt, wie viel Prozent der Werte in einem bestimmten Bereich auftreten. Nun hängt dieser Bereich jedoch nicht mehr von µ und σ ab, sondern ist standardisiert.
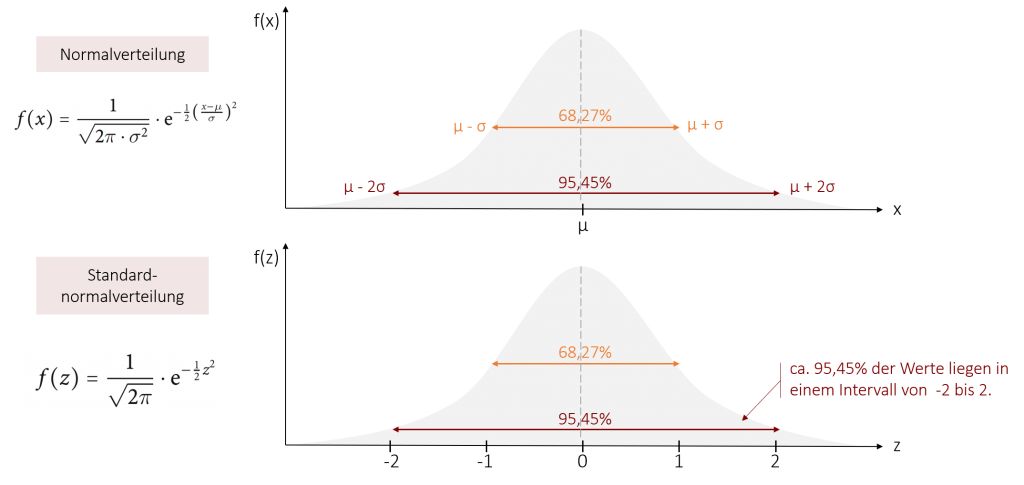
So liegen im Wertebereich zwischen z = -1 und z = +1 immer ca. 68,27% der Werte. Oder anders ausgedrückt: Mit einer Wahrscheinlichkeit von 68,27% liegt der Wert in dem Bereich zwischen -1 und +1.
Doch nun genug von der Theorie. Wie sieht das Ganze in der Praxis aus? Wie können wir solche Intervalle aus Tabellen ablesen? Schauen wir uns dies an einem Beispiel an:
Nehmen wir an, wir haben eine Maschine gekauft die Burger-Patties in großen Mengen herstellen kann. Die Maschine ist jedoch nicht sehr akkurat und so schwankt die Dicke der Fleischscheiben mit einer Standardabweichung von 10mm um den Mittelwert von 40mm herum (Es handelt sich um unsere großen XXL-Burger). Wir nehmen bei der Verteilung der Dicke eine Normalverteilung an. Damit haben wir eine Normalverteilung mit µ=40mm und σ=10mm gegeben. Nun möchten wir herausfinden, wie wahrscheinlich es ist, dass ein Burger-Patty mit einer Dicke von 35 – 42 mm produziert wird (oder mathematisch ausgedrückt: P(35 ≤ X ≤ 42) ). Graphisch könnten wir die Aufgabe wie folgt abbilden:
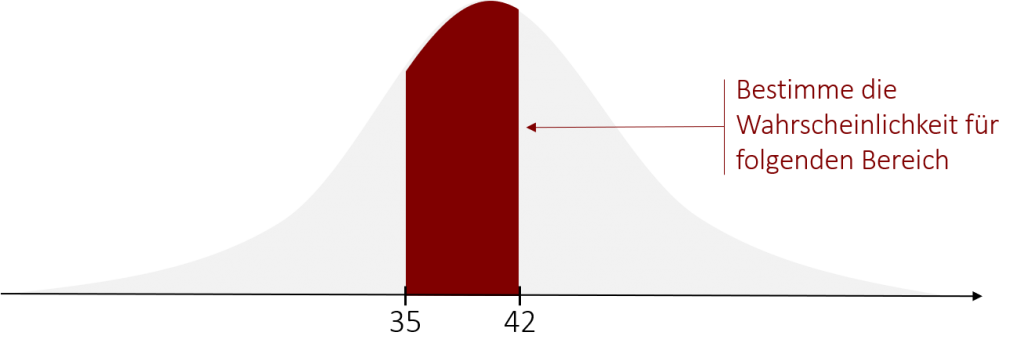
Der erste Schritt wäre diese Normalverteilung in eine Standardnormalverteilung zu überführen, um dadurch die Wahrscheinlichkeit für den Wertebereich in einer Tabelle auslesen zu können. Durch die z-Standardisierung werden so unsere Bereichsgrenzen (35 und 42mm) in z-Werte umgewandelt:

Graphisch betrachtet würde sich unser gesuchter Bereich nun wie folgt ändern:
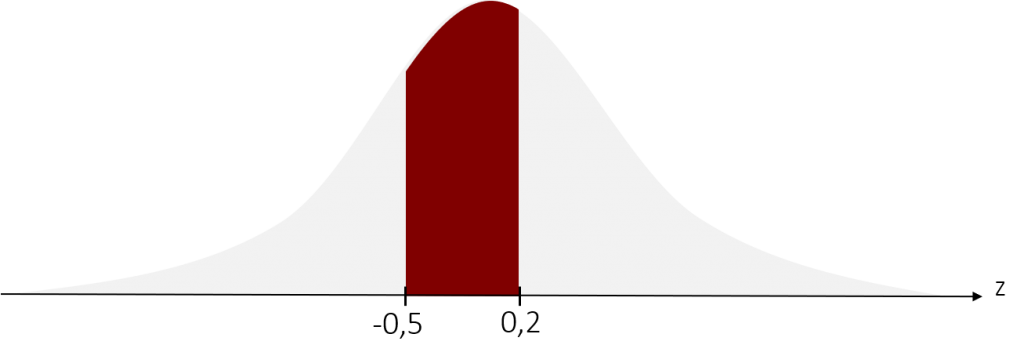
Wir berechnen also die Wahrscheinlichkeit für den Bereich von z = -0,5 bis z = 0,2. Dazu benutzen wir die schon erwähnten Tabellen, die Dichteeigenschaften der Standardnormalverteilung beinhalten. In diesem Tabellen haben fleißige Statistiker bereits alle üblichen Integrale unter der Standardnormalverteilung für Sie berechnet und die entsprechenden Wahrscheinlichkeiten angegeben. Sie finden diese im Anhang zu diesem Buch oder jedem anderen Statistik-Lehrbuch oder im Internet. Schauen wir uns zunächst ihren Aufbau an. In der obersten Zeile und Spalte sehen wir die z-Werte. In den übrigen Zellen ist die Wahrscheinlichkeit abgebildet, dass ein solcher oder kleiner z-Wert auftritt. Was einer Fläche von – bis z entspricht. Für diese Wahrscheinlichkeiten bei der Standardnormalverteilung wird in der Literatur oft der griechische Buchstaben Φ (phi) angegeben, welchen wir im Folgenden hier auch verwenden werden. Die Wahrscheinlichkeit, dass z = 0,2 oder ein kleinerer Wert auftritt, ist beispielsweise Φ(0,2) = 0,5793 (=57,93%).

Wie Ihnen bestimmt aufgefallen ist, werden nicht alle z-Werte in der Tabelle aufgeführt, sondern nur die Positiven. Wenn wir die Wahrscheinlichkeit eines negativen z-Wertes erfahren möchten, müssen wir deshalb einen Zwischenschritt machen. Es gilt:
Φ(-z) = 1 – Φ(z)
In unserem Beispiel möchten wir die Wahrscheinlichkeit für unsere untere Intervallgrenze mit z=-0,5 ausrechnen. Deshalb rechnen wir: Φ(-0,5) = 1 – Φ(0,5) = 1 – 0,6915 = 0,3085 (=30,85%)
Kommen wir nun zur Berechnung der Wahrscheinlichkeit unseres Bereichs. Dazu müssen wir von der Wahrscheinlichkeit, dass z = 0,2 oder ein kleiner Wert auftritt (roter Bereich unter der Kurve) die Wahrscheinlichkeit, dass z = -0,5 oder ein kleinerer Wert auftritt (schwarz schraffierter Bereich unter der Kurve) subtrahieren.
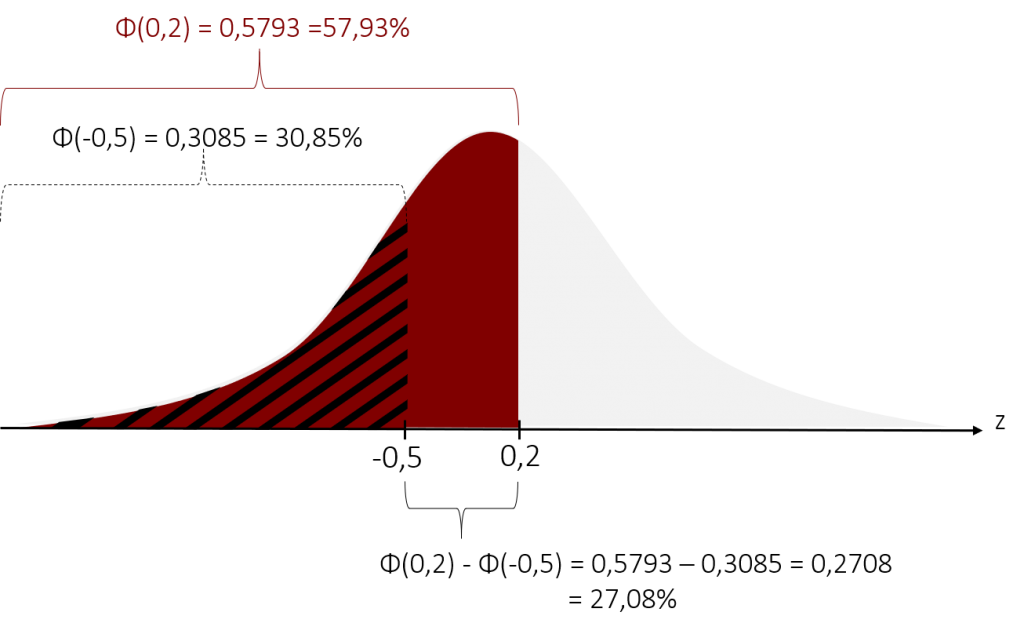
Wenn wir zurück auf unsere Aufgabenstellung schauen, so können wir nun sagen, dass mit einer Wahrscheinlichkeit von 27,08% ein Burger-Patty mit einer Dicke zwischen 35mm und 42mm von unserer Maschine produziert wird.
Mithilfe solcher Tabellen können wir nicht nur Wahrscheinlichkeiten für Intervalle bestimmen, sondern alle möglichen Aufgabenstellungen berechnen. Im Folgenden finden Sie eine kleine Übersicht über solche Aufgabenstellungen und ihre mathematische Herangehensweise:
| P(z1 ≤ X ≤ z2) | = Φ(z2) – Φ(z1) |
| P(X ≤ z) | = Φ(z) |
| P(X ≥ z) | = 1 – Φ(z) |
Rechenbeispiele für Intervalle
Nehmen wir als Beispiel nochmal unsere bereits erwähnte Burger-Maschine. Diese produziert Burger-Patties mit einem Erwartungswert von μ = 40mm und σ = 10mm. Wir setzen eine Normalverteilung voraus.
1. Wie wahrscheinlich ist es, dass unser Burger-Patty kleiner als 30mm ist?
Zunächst machen wir eine z-Standardisierung:
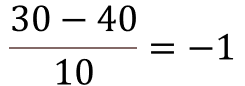
Nun rechnen wir die Wahrscheinlichkeit aus: P(X < -1) = Φ(-1) = 1 – Φ(1) = 1 – 0,8413 = 0,1587
Die Wahrscheinlichkeit, dass unser Burger-Patty kleiner als 30mm ist, beträgt 15,87%.
2. Wie wahrscheinlich ist es, dass unser Burger-Patty größer als 45mm ausfällt?
Zunächst machen wir eine z-Standardisierung:
![]()
Nun rechnen wir die Wahrscheinlichkeit aus: P(X > 0,5) = 1 – Φ(0,5) = 1 – 0,6915 = 0,3085
Unser Brett fällt mit einer Wahrscheinlichkeit von 30,85% größer als 45mm aus.
Fazit des Exkurses
Ziel des Exkurses war es Ihnen aufzuzeigen, welche Verteilungsformen in der Wahrscheinlichkeitsrechnung existieren und wie man mit ihrer Hilfe Wahrscheinlichkeitsaussagen treffen kann. So können Sie nun die Wahrscheinlichkeit für ein bestimmtes Intervall angeben oder ein Intervall bestimmen, welches eine bestimmte Wahrscheinlichkeit besitzt.
Kommen wir jedoch zurück zu unserem ursprünglichen Thema: der Intervallschätzung. Ihr Ziel ist es einen Bereich zu schätzen, in dem ein gesuchter Populationsparameter mit einer vordefinierten Wahrscheinlichkeit liegt. Hierzu müssen wir, wie wir soeben gesehen haben, die Verteilung der Daten kennen. In der Praxis stellt jedoch genau das ein Problem dar. Oftmals ist die Verteilung der Daten in der Grundgesamtheit unbekannt, wodurch Wahrscheinlichkeitsaussagen theoretisch nicht möglich wären. Um dennoch eine Intervallschätzung vornehmen zu können, hilft uns das zentrale Grenzwerttheorem.
9.3 Zentrales Grenzwerttheorem
Das zentrale Grenzwerttheorem besagt, dass unabhängig von der Verteilung der Daten in der Grundgesamtheit die Stichprobenkennwerteverteilung der Mittelwerte mit wachsendem Stichprobenumfang in eine Normalverteilung übergeht.
Was bedeutet dies genau? Stellen sie sich folgende Populationsverteilung vor:
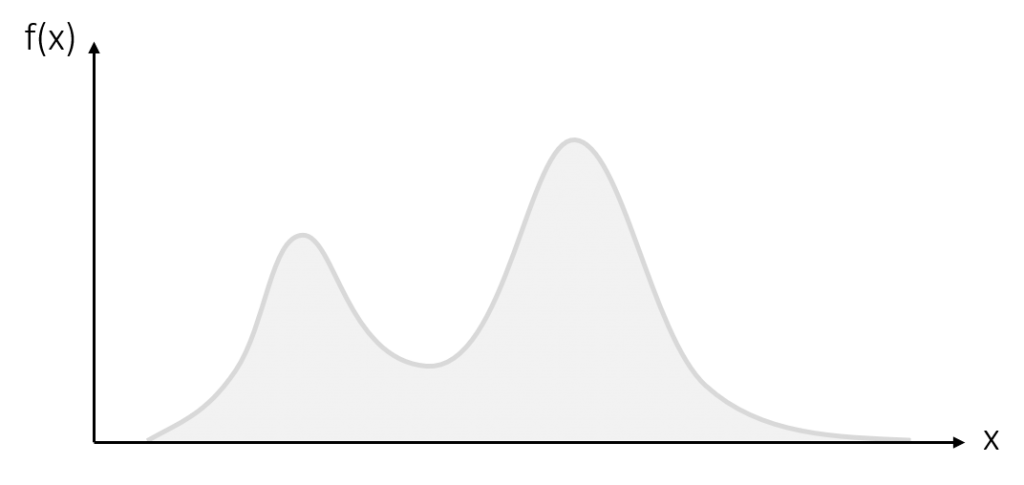
Nun ziehen wir aus dieser Population (hypothetisch) unendlich viele Stichproben und berechnen für jede Stichprobe den Mittelwert. Wenn wir diese Mittelwerte daraufhin in einer Verteilung abbilden, erhalten wir eine Stichprobenkennwerteverteilung der Mittelwerte, die wie folgt aussieht:
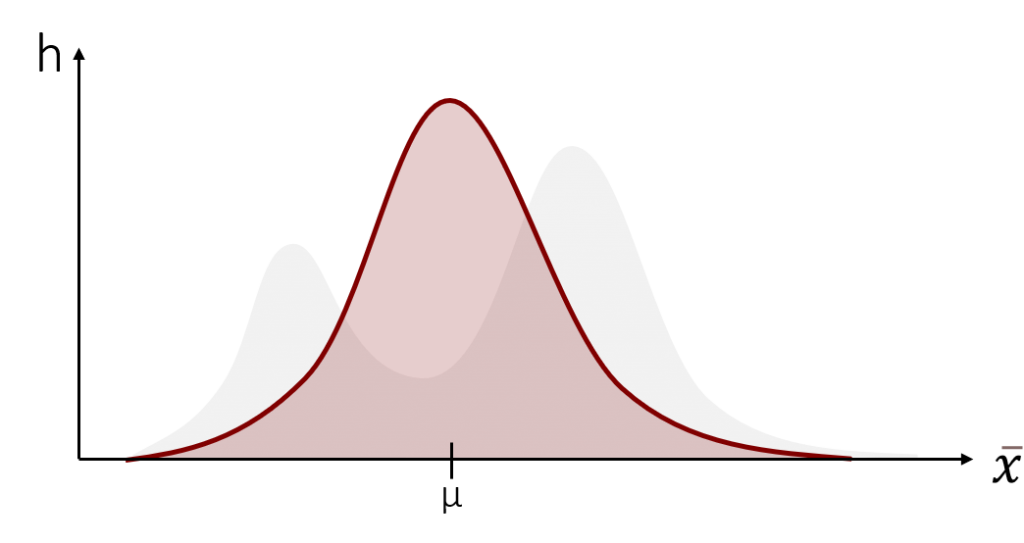
Heureka! Wir sehen, dass die Stichprobenkennwerteverteilung einer Normalverteilung entspricht und nicht wie die ursprüngliche Datenverteilung aussieht. Dies passiert, da der Mittelwert als erwartungstreuer Schätzer zufällig um den wahren Populationsmittelwert μ schwankt und dadurch bei genügend vielen oder genügend großen Stichproben automatisch eine Normalverteilung abbildet. Aus diesem Grund können wir bei einer genügend großen Stichprobe eine Normalverteilung für die Stichprobenkennwerteverteilung unterstellen, obwohl wir die eigentliche Verteilung der Daten nicht kennen. Genügend große Stichprobe bedeutet dabei üblicherweise mindestens n > 30. Diese Zahl ist jedoch eine Konvention in der Wissenschaft (also ein Wert, auf den man sich in der gelebten Praxis geeinigt hat) und kein Bestandteil des Grenzwerttheorems selbst.
Wichtig zu beachten ist hierbei, dass das zentrale Grenzwerttheorem nur für die Kennwerteverteilung der Mittelwerte gilt. Bei anderen Kennwerten wie z.B. dem Median, der Standardabweichung oder des Prozentwerts hängt die Verteilungsform auch bei größeren Stichproben von der Verteilung des Merkmals in der Grundgesamtheit ab.
Um für Sie das zentrale Grenzwerttheorem noch einmal zu veranschaulichen, zeigen Ihnen die folgenden Videos die Thematik anhand praktischer Beispiele:
9.2 Konfidenzintervall | Zentrales Grenzwerttheorem
Da wir nun dank des zentralen Grenzwerttheorems von einer Normalverteilung bei der Kennwerteverteilung der Mittelwerte ausgehen können, haben wir die Frage um die Verteilungsform geklärt und können somit zum nächsten Schritt übergehen: Der Konstruktion eines (symmetrischen) Konfidenzintervalls, um sagen zu können, mit welcher Wahrscheinlichkeit ein Parameter (z.B. μ ) zu erwarten ist, wenn man einen bestimmten Mittelwert in einer Stichprobe findet.
9.4 Konfidenzintervalle berechnen
Das Konfidenzintervall ist ein Intervall, in dem der gesuchte Populationsparameter mit einer bestimmten (und im Vorhinein festgelegten) Wahrscheinlichkeit liegt. Die festgelegte Wahrscheinlichkeit wird auch als Konfidenzkoeffizient bezeichnet und beträgt beispielsweise 95%. Gegenstück zum Konfidenzkoeffizienten ist die Gegenwahrscheinlichkeit α. Sie ist der Fehler, den wir bereit sind einzugehen und beträgt bei einem 95%-Konfidenzkoeffizienten = 5%. Es gilt somit: Konfidenzkoeffizient = 1 – α.
Um die Logik des Konfidenzintervalls besser zu verstehen, nähern wir uns seiner Konstruktion mit Hilfe eines Beispiels. Nehmen wir an, wir möchten die durchschnittliche YouTube-Nutzungsdauer pro Tag mit einer 95%-Wahrscheinlichkeit bestimmen. Dafür nehmen wir eine repräsentative Stichprobe von 100 Personen und können aufgrund der ausreichend großen Stichprobe (n>30) eine Normalverteilung unterstellen.
Ausgangspunkt unseres 95%-Konfidenzintervalls ist eine erwartungstreue Punktschätzung, die durch unseren Stichprobenmittelwert ( = 40 Minuten pro Tag) gegeben ist.
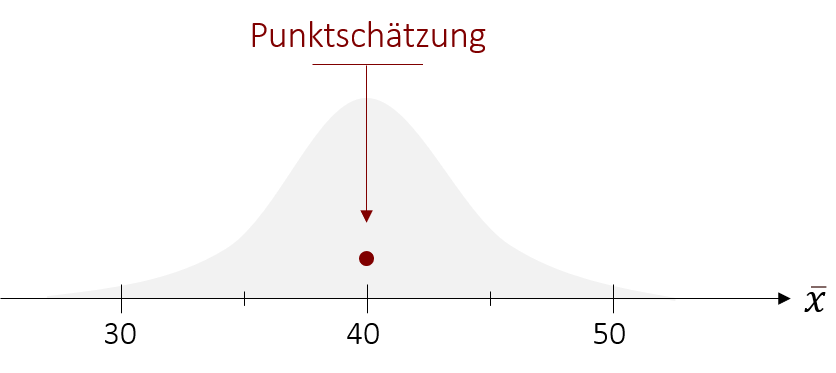
Jetzt fehlt nur noch das symmetrische Intervall um diese Punktschätzung herum. Hierfür ziehen wir unsere Erkenntnisse aus unserem Exkurs zu Rate. Dort haben wir gelernt, dass in einer Normalverteilung festgelegt ist, wie viel Prozent der Werte in einem bestimmten Bereich auftreten. Genau dasselbe gilt auch für unsere Verteilung der Mittelwerte, die aufgrund des zentralen Grenzwerttheorems ebenfalls eine Normalverteilung widerspiegelt. Unsere Aufgabe ist es nun den Bereich in der Normalverteilung zu bestimmen, in dem 95% der Werte liegen. Wichtig dabei ist, dass der Bereich symmetrisch sein soll und demensprechend unsere Punktschätzung im Mittelpunkt liegen muss.
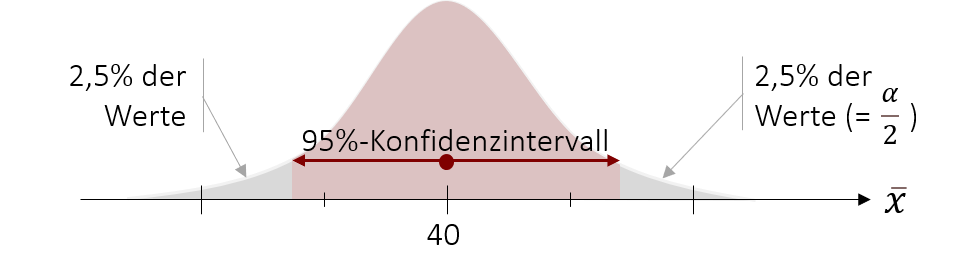
Wie wir in der Grafik sehen, teilt sich aufgrund der Symmetrie des Intervalls die Gegenwahrscheinlichkeit α in zwei Hälfen auf. In unserem Beispiel liegt somit die 5%-Gegenwahrscheinlichkeit nicht auf einer Seite, sondern teilt sich in jeweils 2,5% auf beiden Seiten auf. Wenn wir also die Grenzen unseres 95%-Konfidenzintervalls definieren möchten, müssen wir wissen bis zu welchem Punkt 2,5% unserer Werte liegen und bis zu welchem Punkt 97,5% unserer Werte liegen.
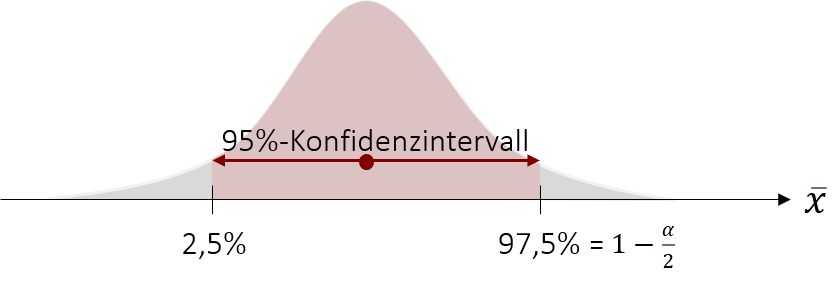
Ebenso wie im Exkurs ziehen wir hierzu die Tabellen heran, in denen die Wahrscheinlichkeit abgebildet ist, dass ein bestimmter oder kleinerer z-Wert auftritt. Dort suchen wir nun den z-Wert, der die Wahrscheinlichkeit von 97,5% (=0,975) aufweist.

Wir sehen, dass ein z-Wert von z=1,96 die gegebene Wahrscheinlichkeit besitzt. Doch wie finden wir den z-Wert heraus, bis zu dem 2,5% der Werte liegen? Durch die Symmetrie der Normalverteilung müssen wir lediglich das Vorzeichen ändern, um die entsprechenden z-Wert zu bestimmen.
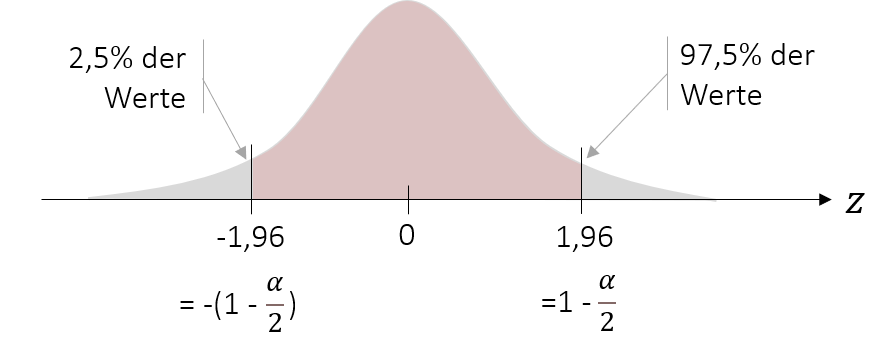
Wenn wir eine Standardnormalverteilung hätten, wären wir an diesem Schritt fertig. Unser 95%-Konfidenzintervall würde einen Bereich von [-1,96 ; +1,96] abdecken. Um jedoch die eigentliche Aufgabenstellung zu beantworten, hilft uns dieses Wissen nur wenig. Damit wir unseren Mittelwert der YouTube-Nutzungsdauer eingrenzen können, müssen wir die Grenzen der Standardnormalverteilung auf unsere Stichprobenmittelwertverteilung übertragen. Da sie jedoch nicht standardisiert ist und damit von μ (bzw. in unserer Schätzung von ) und σ abhängt, müssen wir unser bisheriges Intervall um diese Variablen ergänzen. Dadurch wird aus unserem [-1,96 ; +1,96] Intervall ein Bereich, welcher folgende Grenzen enthält:
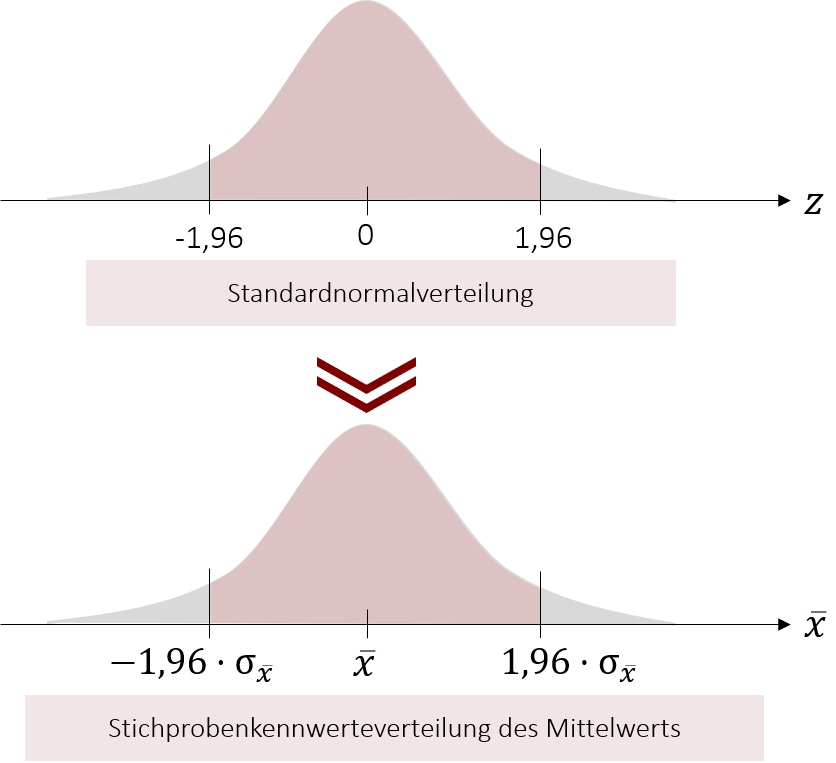
Jetzt müssen wir nur noch und σx eintragen und schon haben wir die Grenzen unseres Konfidenzintervalls definiert. ist mit 40 Minuten pro Tag bereits bekannt, die Standardabweichung der Stichprobenkennwerteverteilung müssen wir hingegen noch ausrechnen. Wer sich an das letzte Kapitel erinnert, weiß, dass die Formel hierfür wie folgt lautet:
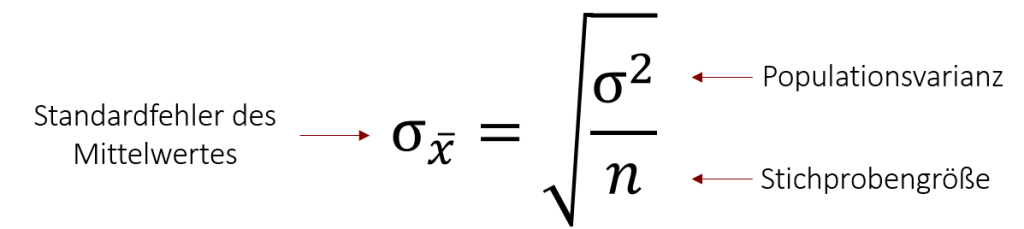
Nehmen wir an, dass die Populationsvarianz mit σ2 = 400 bekannt ist, sodass wir alle nötigen Variablen einsetzen können. So erhalten wir folgenden Standardfehler:
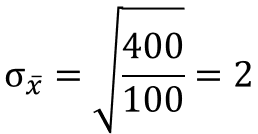
Nun können wir die Grenzen unseres Konfidenzintervalls berechnen:
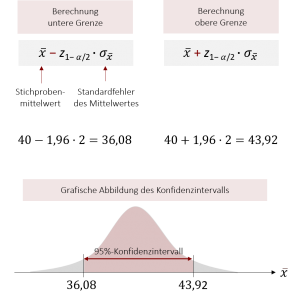
Abschließend können wir aussagen, dass mit einer Wahrscheinlichkeit von 95% die durchschnittliche YouTube-Nutzungsdauer in der Grundgesamtheit zwischen 36,08 Minuten und 43,92 Minuten liegt.
Allgemein formuliert lautet die Formel für ein beidseitiges Konfidenzintervall für den Parameter μ mit der Wahrscheinlichkeit 1- α (wenn die Populationsvarianz bekannt ist und eine Normalverteilung unterstellt werden kann) wie folgt:
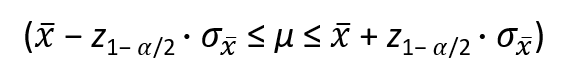
Rechenbeispiel Konfidenzintervall
An einer repräsentativen Stichprobe von 100 Personen wird ein Test zur Ermittlung der Koordinationsfähigkeit durchgeführt. Die Testleistungen haben einen Mittelwert von = 80 und die Populationsvarianz wird auf σ2 = 400 geschätzt.
Nun möchten wir herausfinden, in welchem Bereich μ mit einer Wahrscheinlichkeit von 95% liegt.
Zunächst bestimmen wir den z-Wert an unserer oberen Intervallgrenze: Da wir ein 95%-Konfidenzintervall berechnen möchten, interessiert uns der z-Wert mit einer Wahrscheinlichkeit von 97,5% (1-α/2). Wenn wir in die Tabelle schauen, sehen wir, dass 1,96 der gesuchte z-Wert ist.
Als Nächstes rechnen wir den Standardfehler des Mittelwertes aus: 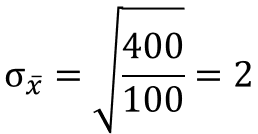
Nun setzen wir die berechneten Variablen in die Formel für die Intervallgrenzen ein:
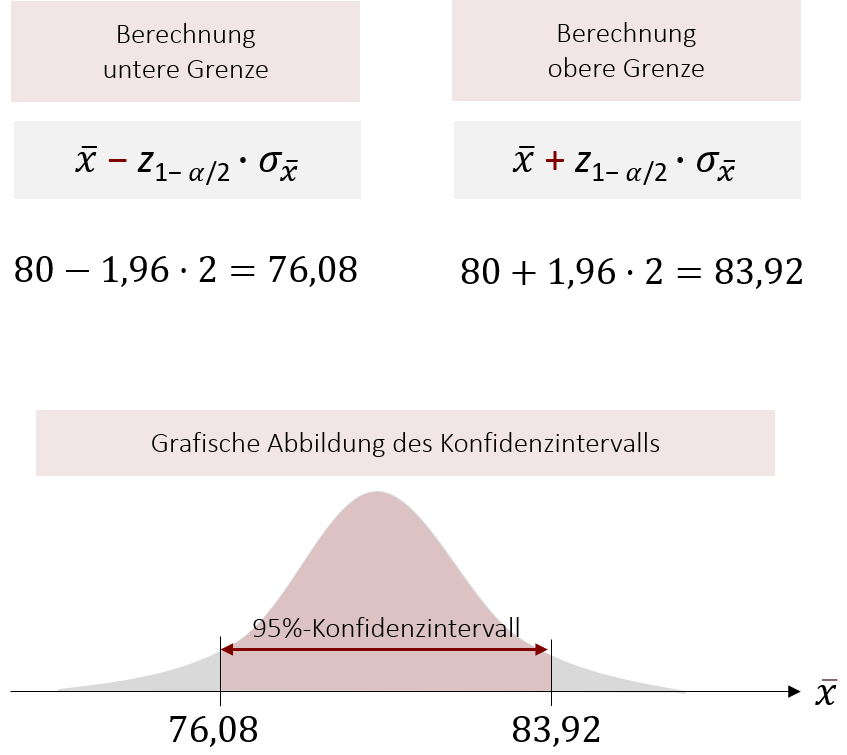
Mit einer Wahrscheinlichkeit von 95% liegt μ zwischen 76,08 und 83,92.
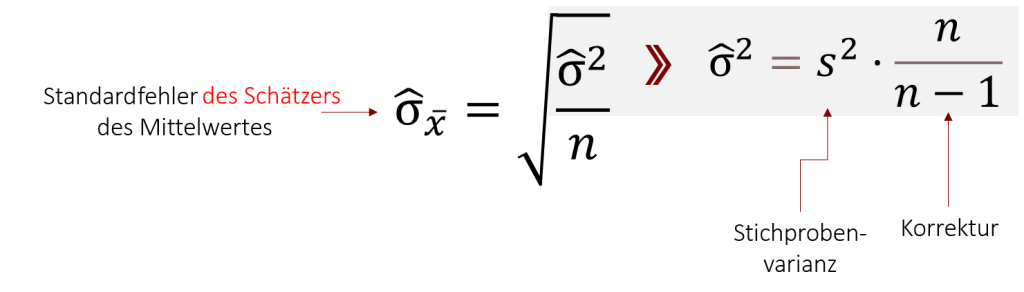
Wir haben jedoch nicht immer den Luxus die Populationsvarianz zu kennen. In manchen Fällen müssen wir aus diesem Grund den Standardfehler des Schätzers des Mittelwerts auf Basis der Stichprobenvarianz mittels folgender Formel schätzen:
Expertenwissen Konfidenzintervalle mit T-Verteilung
Ist die Populationsvarianz nicht bekannt, entspricht die Stichprobenkennwerteverteilung des Mittelwerts zudem nicht mehr einer Normalverteilung, sondern eher einer t-Verteilung. Aus diesem Grund muss man statt der z-Werte, die wir bei der Normalverteilung ablesen, die Werte für die t-Verteilung benutzen. Beim Ablesen sollte jedoch beachtet werden, dass es für jede Stichprobengröße eine eigene t-Verteilung gibt. Das beidseitige Konfidenzintervall lautet nun:
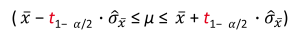
Um das Thema Konfidenzintervalle im Gesamten anhand eines anschaulichen Beispiels besser nachvollziehen zu können, stehen Ihnen die folgenden Videos zur Verfügung. Sie bauen aufeinander auf, weshalb es sich lohnt, sie in der vorgegebenen Reihenfolge anzuschauen.
9.4 Konfidenzintervall | Konstruktion des Konfidenzintervalls
9.5 Konfidenzinterval | Bestimmung des Konfidenzkoeffizienten
9.6 Konfidenzintervall | Berechnung des Konfidenzintervalls
9.7 Konfidenzintervall | Rechen-Beispiel
In diesem Buchkapitel haben Sie gelernt, auf welcher Logik die Intervallschätzung basiert und wie Sie Konfidenzintervalle für den Mittelwert ausrechnen können. Man kann jedoch auch andere Parameter mittels Konfidenzintervalle schätzen, wie z.B. die Varianz, Standardabweichung, Häufigkeiten und noch einige mehr. Die Formeln weichen hierfür zum Teil erheblich von der ab, die Sie für den Mittelwert gelernt haben. In der Praxis wird bei der Berechnung von Konfidenzintervallen für solche Kennwerte jedoch meist gar kein mathematisches Verfahren genutzt, sondern das sogenannte Bootstrapping durchgeführt. Das Bootstrapping-Verfahren werden wir zum Abschluss dieses Kapitels noch genauer besprechen, zunächst wollen wir uns jedoch der Berechnung des Konfidenzintervalls in SPSS widmen.
9.5 Konfidenzintervalle in SPSS berechnen und (grafisch) ausgeben
Konfidenzintervalle für den Mittelwert sowie der Standardfehler lassen sich in SPSS recht einfach ausgeben. Hierfür gehen Sie in folgendes Menü:
Analysieren > Deskriptive Statistiken > Explorative Datenanalyse.
Sie ziehen die interessierende Variable einfach in das Feld Abhängige Variable und können bei Bedarf noch im Feld Faktorenliste eine Gruppierungsvariable auswählen um z.B. die Konfidenzintervalle getrennt für Männer und Frauen berechnen zu lassen. Standardmäßig wird Ihnen hierbei der Standardfehler des Schätzers des Mittelwerts sowie das 95%-Konfidenzintervall ausgegeben. Weitere Konfidenzintervalltypen können Sie mit einem Klick auf Statistiken einstellen. Das folgende Video zeigt dies an einem Beispiel.
Video 9.10 Konfidenzintervalle und Standardfehler in SPSS berechnen
Konfidenzintervalle lassen sich in SPSS auch sehr schön graphisch visualisieren. Hierzu dient der übliche Diagramm-Assistent, der in folgendem Menü zu finden ist:
Grafik > Diagrammerstellung.
Hierbei sollte der Diagrammtyp Einfache Fehlerbalken ausgewählt werden, welcher als Standardeinstellung bereits das 95%-Konfidenzintervall anzeigt. Das folgende Video zeigt dies wieder an einem Beispiel:
Video 9.11 Konfidenzintervalle grafisch in SPSS darstellen und berechnen
9.6 Konfidenzintervalle mit dem Bootstrapping Verfahren
Bootstrapping ist eine Möglichkeit, mithilfe schierer Rechenleistung, dafür fast ganz ohne Mathematik, Konfidenzintervalle zu generieren. Hierbei werden aus einer bestehenden Stichprobe sehr viele (meist über 1000) neue Stichproben generiert und daraus eine „echte“ Kennwerteverteilung generiert, aus der man das Intervall direkt ablesen kann. Dies hat den Vorteil, dass das Verfahren nicht auf der Annahme der Normalverteilung der Stichproben-Kennwerteverteilung basiert und daher auch für kleine Stichproben nutzbar ist. Doch wie erzeugt ein PC Programm (wie SPSS) aus nur einer Stichprobe mehrere tausend neue Stichproben? Das Geheimnis dabei ist, dass diese neuen Stichproben mit zurücklegen gezogen werden. Nehmen wir an, die Ursprungsstichprobe beinhaltet 10 Personen. SPSS generiert nun daraus neue Stichproben bei der jedes Mal eine Person gezogen wird und jede der 10 Personen immer die gleiche Chance hat gezogen zu werden (nämlich1/10). Dadurch kann eine Person mehrmals in einer Stichprobe landen oder im Extremfall eine Stichprobe aus nur einer einzigen Person bestehen, die zufällig zehn Mal hintereinander gezogen wurde. Das folgende Video veranschaulicht dieses Verfahren:
Video 9.8 Konfidenzintervalle mit dem Bootstrapping Verfahren
9.7 Konfidenzintervalle mit dem Bootstrapping Verfahren in SPSS berechnen
Die Berechnung von Bootstrapping Konfidenzintervallen lässt sich in SPSS sehr komfortabel für fast alle Kennwerte aktivieren. Hierfür muss nur im jeweiligen Menü der Button Bootstrap gedrückt werden und auf Bootstrapping durchführen geklickt werden. In der Praxis bietet sich das sog. BCa (Bias-Corrected and Accelerated) Verfahren an, da dieses schneller läuft und auch eine robustere Abschätzung für das Konfidenzintervall liefert. Das folgende Video zeigt die Durchführung in SPSS.
Video 9.9 Konfidenzintervalle mit Bootstrapping in SPSS
9.8 Übungsfragen
Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!
In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!
9.9 Übungsaufgaben
Übungsaufgabe 1
Wir haben eine Stichprobe von n=40 Burgerkunden nach Ihrem Alter gefragt und wollen hieraus eine Intervallschätzung für das Alter in der Population berechnen. Wir haben in der Stichprobe einen Mittelwert von 23,5 Jahren und einen Standardfehler von 0,55.
Wie ist das 90- und 95-Prozent Konfidenzintervall für das Alter unserer Burgerkunden?
Die Lösung finden Sie Schritt-für-Schritt im folgendem Video:
Übungsaufgabe 2
Bitte interpretieren Sie folgenden Output:




