Statistik mit R & RStudio
27 Mixed-ANOVA mit R
Mixed-ANOVA
Einführung
Bei einer gemischten Varianzanalyse haben wir mindestens einen Faktor, der messwiederholt vorliegt und einen Faktor, der unabhängig ist. Bei einer Mixed-ANOVA spricht man zum einen vom Within-Subjects-Faktor, also dem Faktor, bei dem dieselben Versuchspersonen unter verschiedenen Bedingungen, wie z. B. Zeit oder verschiedene Niveaus einer unabhängigen Variable, getestet werden. Zum anderen gibt es den Between-Subject-Faktor, bei dem verschiedene Probanden unter verschiedenen Bedingungen getestet werden, z. B. verschiedene Gruppen oder Behandlungen.
Zum Beispiel könnte das bedeuten, dass wir Unterschiede zwischen zwei Gruppen (z. B. Männer und Frauen) betrachten und Unterschiede zwischen den Messzeitpunkten (morgens und abends). Das Geschlecht wäre der Between-, die Zeit der Within-Faktor..
Mit der Mixed-ANOVA können wir auf Haupteffekte der Faktoren innerhalb der Versuchspersonen und zwischen den Versuchspersonen sowie auf deren Wechselwirkungen testen.
Die Mixed-ANOVA kombiniert die Voraussetzungen der einfaktoriellen ANOVA (Homogenität der Varianzen zwischen den Gruppen) mit den Voraussetzungen der Messwiederholungs-ANOVA (Sphärizität zwischen den Messzeitpunkten).
Beispiel
Wir haben drei verschiedene Fleischpatties für Burger (regional, bio, demeter), die wir verkosten lassen und auf einer subjektiven Geschmacksskala von 1 (schmeckt gar nicht) bis 5 (schmeckt super) bewerten lassen. Hierzu isst jeder Proband nacheinander alle 3 Burger und gibt seine Bewertung ab (Reihenfolge variiert). Zusätzlich interessiert uns, ob Männer und Frauen die Burger anders bewerten. Wir haben also sowohl einen Between-Faktor (Geschlecht) als auch einen Within-Faktor (Fleischart).
Daten laden
burger <- read.csv2(file="Burger.csv")Auch hier werden die Variablen Geschlecht und Fleischart nicht korrekt eingelesen. Wir wandeln diese in Faktoren um.
burger$Geschlecht <- as.factor(burger$Geschlecht)
burger$Fleischart <- as.factor(burger$Fleischart)Voraussetzungen
Bei einer gemischten Varianzanalyse müssen die Voraussetzungen von beiden ANOVA-Arten getestet werden. Dies bedeutet, wir müssen die Sphärizität für die Messzeitpunkte testen (Mauchly-Test), als auch die Varianzhomogenität zwischen den Gruppen (Levene-Test).
Da der Mauchly-Test beim afex Paket automatisch mitgetestet wird, müssen wir also nur den Levene-Test durchführen.
library(car)
leveneTest(Bewertung ~ Geschlecht, data=burger)
## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 1 0.7608 0.3867
## 58Der Test wird nicht signifikant, daher können wir von Varianzhomogenität ausgehen.
ANOVA durchführen
Nun führen wir die ANOVA mit der Funktion aov_car aus dem Paket afex aus. Die Funktion benötigt die folgenden Argumente:
Die gemischte Varianzanalyse führen wir wieder mit der aov_car-Funktion aus dem
afex-Paket durch, die wir auch für die Varianzanalyse mit Messwiederholung verwendet haben. Die messwiederholte Variable (Within-Faktor) kommt vor die Tilde, die nicht-messwiederholte Variable (Between-
Faktor) kommt direkt hinter der Tilde. Die Zuordnung der ID (hier Person) kommt im Error-Term vor dem Querstrich, die Zuordnung der Messzeitpunkte (hier Fleischart) folgt hinter dem Querstrich.
ANOVA4 <- aov_car(Bewertung ~ Geschlecht + Error(Person/Fleischart), data=burger)
## Contrasts set to contr.sum for the following variables: Geschlecht
summary(ANOVA4)
##
## Univariate Type III Repeated-Measures ANOVA Assuming Sphericity
##
## Sum Sq num Df Error SS den Df F value
## (Intercept) 629.79 1 6.2854 18 1803.5937
## Geschlecht 7.77 1 6.2854 18 22.2483
## Fleischart 9.24 2 15.6612 36 10.6162
## Geschlecht:Fleischart 4.39 2 15.6612 36 5.0475
## Pr(>F)
## (Intercept) < 0.00000000000000022 ***
## Geschlecht 0.0001720 ***
## Fleischart 0.0002376 ***
## Geschlecht:Fleischart 0.0116859 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Mauchly Tests for Sphericity
##
## Test statistic p-value
## Fleischart 0.95516 0.6771
## Geschlecht:Fleischart 0.95516 0.6771
##
##
## Greenhouse-Geisser and Huynh-Feldt Corrections
## for Departure from Sphericity
##
## GG eps Pr(>F[GG])
## Fleischart 0.95709 0.0003043 ***
## Geschlecht:Fleischart 0.95709 0.0129054 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## HF eps Pr(>F[HF])
## Fleischart 1.068308 0.0002376261
## Geschlecht:Fleischart 1.068308 0.0116859190Wir sehen, dass alle drei Effekte signifikant werden. Es gibt also sowohl einen signifikanten Unterschied zwischen den drei Fleischarten als auch zwischen den Geschlechtern. Da jedoch auch der Interaktionseffekt signifikant ist, sollten wir uns diesen genauer ansehen.
PostHoc
Auch bei der Mixed-ANOVA kann das Paket emmeans für Post-hoc-Analysen verwendet werden. Wir nutzen für die Paarvergleiche wieder die Funktion pairs. Wenn wir die Paarvergleiche gruppiert nach Geschlecht ansehen wollen verwenden wir Fleischart|Geschlecht wenn wir umgekehrt die Paarvergleiche gruppiert nach Burgerart ansehen wollen können wir Geschlecht|Fleischart verwenden. Mit einem „*“ zwischen den Variablen erhalten wir alle Kombinationsmöglichkeiten (Dies ist jedoch sehr unübersichtlich).
ph_mix <- emmeans(ANOVA4, ~ Fleischart|Geschlecht)
pairs(ph_mix)
## Geschlecht = Frau:
## contrast estimate SE df t.ratio p.value
## X1.regional - X2.bio -0.909 0.277 18 -3.285 0.0109
## X1.regional - X3.demeter -1.595 0.281 18 -5.671 0.0001
## X2.bio - X3.demeter -0.686 0.325 18 -2.113 0.1152
##
## Geschlecht = Mann:
## contrast estimate SE df t.ratio p.value
## X1.regional - X2.bio -0.395 0.277 18 -1.428 0.3483
## X1.regional - X3.demeter -0.280 0.281 18 -0.996 0.5890
## X2.bio - X3.demeter 0.115 0.325 18 0.354 0.9334
##
## P value adjustment: tukey method for comparing a family of 3 estimatesDie Ergebnisse der Paarvergleiche zeigen zwei signifikante Unterschiede: Einmal bei Frauen zwischen regional und bio und bei Frauen zwischen regional und demeter. Anders ausgedrückt bedeutet das, dass die verschiedenen Fleischarten bei Männern keinen Unterschied in der Zahlungsbereitschaft auslösen. Bei Frauen erhöht sich jedoch die Zahlungsbereitschaft bei bio und bei demeter Fleisch signifikant. Um dies nochmal übersichtlich darzustellen, hilft ein Interaktionsdiagramm.
Grafische Analyse (Interaktionsplot)
Auch hier können wir wieder einen Interaktionsplot dem Paket afex erstellen. Die Notation entspricht dem Beispiel zuvor.
- x: Messwiederholte Variable (Within-Faktor)
- trace: Nicht-messwiederholte Variablen (Between-
Faktor) - error: Art der Konfidenzintervalle. Für Between-Vergleiche geben wir “between” ein, für Within-Vergleiche “within”.
afex_plot(ANOVA4, x="Fleischart", trace="Geschlecht", error="between")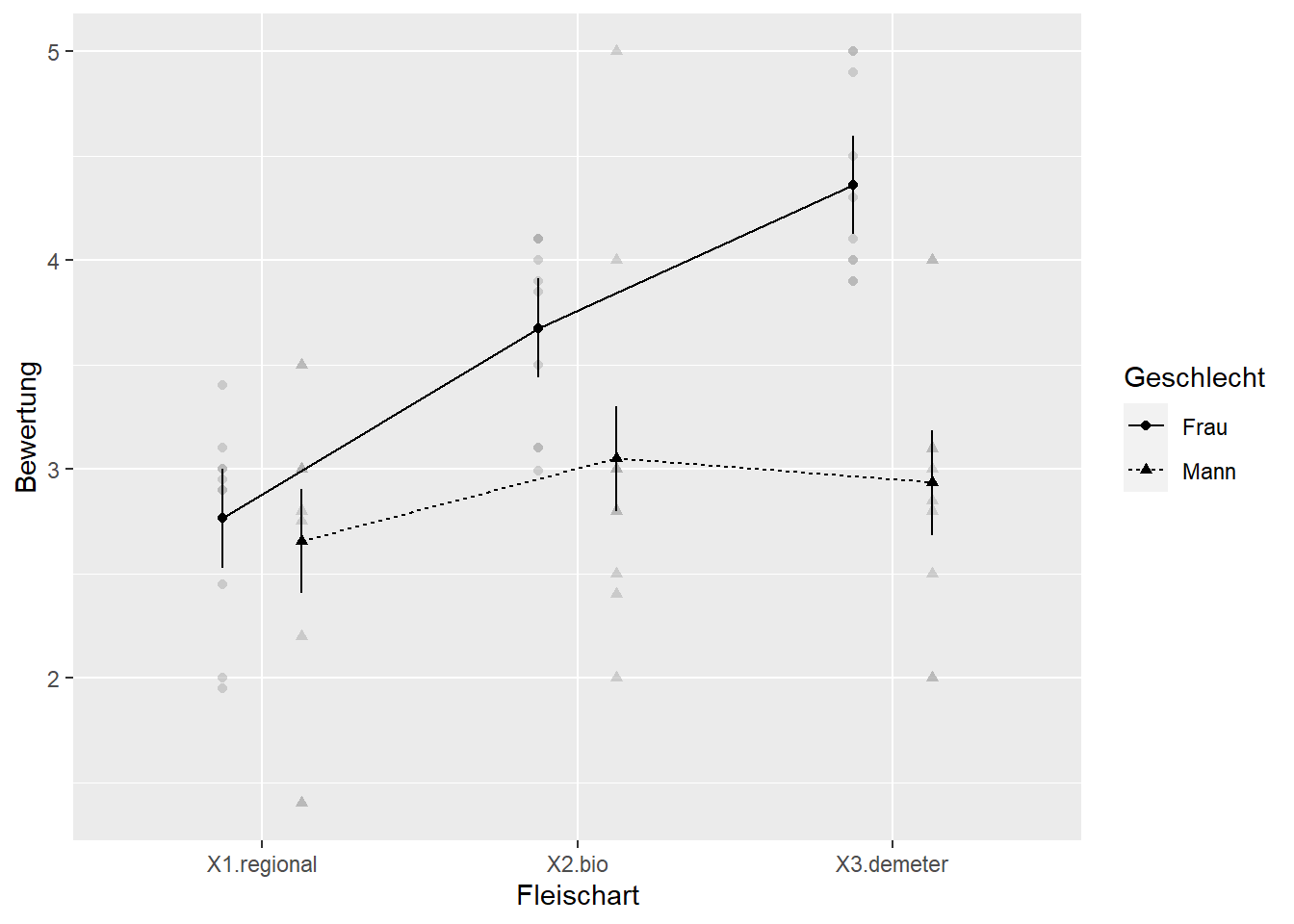
Auch hier sehen wir, dass sich die Bewertung der Fleischarten zwischen Männern und Frauen erheblich unterscheiden. Bei Männern fallen die Bewertungen ähnlich aus, während Frauen bio besser und demeter nochmals besser bewerten.
In diesem Video zeige ich, wie das in R funktioniert:
Übung
Die Daten “Anxiety” zeigen die Angstwerte, die zu drei Zeitpunkten von drei Gruppen von Personen gemessen wurden, die körperliche Übungen auf verschiedenen Niveaus praktizierten (Gruppe 1: normal, Gruppe 2: moderat und Gruppe 3: hoch).
Mit einer gemischten zweifaktoriellen ANOVA soll untersucht werden, ob es bei der Erklärung des Angstwertes eine Wechselwirkung zwischen Gruppe und Zeit gibt.
anxiety <- read.csv("anxiety.csv")
anxiety$time <- as.factor(anxiety$time )
anxiety$group <- as.factor(anxiety$group )
Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.


