Hypothesentests
11 Z-Test/Gaußtest
11.0 Einführung Z-Test/Gaußtest
Zu Beginn von Testverfahren stehen die Hypothesen. Wie solche Hypothesen aussehen können und was für Hypothesen es in der Forschung gibt, haben Sie bereits im letzten Kapitel gelernt. Nun geht es darum, diese anhand von Stichproben zu testen und dadurch zu bestätigen oder zu verwerfen. Da unterschiedliche Hypothesen diverse Sachverhalte postulieren können, gibt es jedoch nicht den einen statistischen Test, der für alle Hypothesen anwendbar ist. Stattdessen finden sich in der Inferenzstatistik zahlreiche Testverfahren, die jeweils für bestimmte Hypothesen geeignet sind. So auch der Z-Test oder Gaußtest, welchen Sie in diesem Kapitel kennenlernen werden.
Der Z-Test gehört hierbei zu den Tests, die auf Basis einer Stichprobe Unterschiedshypothesen bezüglich des Erwartungswerts untersuchen. Er überprüft dabei, ob das arithmetische Mittel eines Merkmals aus einer Stichprobe zu einer Population gehören kann, für die der entsprechende Mittelwert (μ0) bekannt bzw. gegeben ist. Das klingt zunächst kompliziert, jedoch lassen sich hierfür auch viele, sehr praktische, Anwendungsfälle finden, wie die nachfolgenden Beispiele zeigen.
Beispiele Z-Test
Der Betreiber einer Burger-Filiale möchte herausfinden, ob eine neue Cola-Sorte beim Kunden besser ankommt als sein aktuelle Cola-Marke. Der aktuelle Geschmack liegt laut Meinungsumfragen bei μ = 3,6 von 5 Geschmackspunkten (Die Populationsvarianz ist hierbei bekannt). Bei einer Zufalls-Stichprobe von 50 Probanden hat die neuen Cola-Sorte einen Mittelwert von = 4,5 Geschmackspunkten ergeben. Doch reicht dieses Ergebnis aus um nun sagen zu können, dass die neue Cola-Sorte auch wirklich signifikant besser schmeckt als die bisherige? Mit anderen Worten: ist dieser Unterschied auch in der Population so zu erwarten?
Hierbei lauten die Hypothesen:
H0: Die neue Cola-Sorte schmeckt im Durchschnitt gleich oder schlechter als die aktuellen Cola-Sorte.
H1: Die neuen Cola-Sorte schmeckt im Durchschnitt besser als die aktuellen Cola-Sorte.
Sind Abonnenten des FiveProfs YouTube Kanals schlauer als die Durchschnittsbevölkerung? Hierfür wurde eine Zufalls-Stichprobe mit 45 Kanal-Abonnenten durchgeführt, die einen Mittelwert von 105 IQ-Punkten aufwies. Der Durchschnitt in der Bevölkerung ist mit einem Durchschnittswert von 100 IQ-Punkten und einer Standardabweichung von 15 IQ-Punkten bekannt.
In diesem Fall lauten die Hypothesen:
H0: Die Abonnenten des FiveProfs YouTube Kanals haben den gleichen oder einen geringeren IQ als die Durchschnittsbevölkerung.
H1: Die Abonnenten des FiveProfs YouTube Kanals haben einen höheren IQ als die Durchschnittsbevölkerung.
Wie auch schon bei den Konfidenzintervallen ist das Ziel des Hypothesentests, eine Wahrscheinlichkeitsaussage zu treffen. Wie schon zuvor arbeiten wir mit einer vorab definierten Irrtumswahrscheinlichkeit, dem Signifikanzniveau α, welches definiert, ab welcher Wahrscheinlichkeit wir die Hypothesen ablehnen.
Das folgende Video bietet Ihnen die Möglichkeit, nochmal einen Überblick über das Thema zu erhalten und den Z-Test mit weiteren Beispielen veranschaulicht zu bekommen.
11.1 Z-Test Gaußtest | Einführung
Doch wie geht man an die Testung solcher Hypothesen in der Praxis heran? Schauen wir uns die Testdurchführung schrittweise an.
11.1 Hypothesen aufstellen
Bevor wir mit dem Hypothesentest beginnen, bilden wir zunächst eine Forschungshypothese und übersetzen diese anschließend in die dazugehörigen statistischen Hypothesen.
Schauen wir uns das an einem Beispiel an. Nehmen wir an, ein Hersteller hat die Eiscreme-Sorte „Ewiges Eis“ entwickelt, die bei hohen Temperaturen langsamer schmilzt. Nun möchten Sie das Produkt auf den Markt bringen und führen vorab einen Geschmackstest durch. Sie vermuten jedoch, dass Ihre Eiscreme-Sorte durch die neue Mischung deutlich besser schmeckt und führen zur Bestätigung Ihrer These eine Studie mit 36 zufällig gewählten Probanden durch, die Ihre Eiscreme mit durchschnittlich 7,5 von 10 Geschmackspunkten bewerten. In diesem Beispiel nehmen wir an, dass es ausreichend Marktforschung zum Eis-Geschmack gibt, so dass wir aus vorherigen Analysen wissen, dass die bisher erhältliche Eiscreme mit 7,2 von 10 Geschmackspunkten bewertet wird, bei einer Populationsvarianz von σ2 = 0,36. Ihre operationale Alternativhypothese lautet dementsprechend:
H1: Die Eiscreme-Sorte „Ewiges Eis“ erzielt eine höhere Geschmackspunktzahl, als bisher verfügbare Eiscreme.
Daraufhin bilden Sie das logische Gegenteil, die Null-Hypothese:
H0: Die Eiscreme-Sorte „Ewiges Eis“ erzielt die gleiche oder eine schlechtere Geschmackspunktzahl, als bisher verfügbare Eiscreme.
Anschließend leiten Sie daraus die statistischen Thesen ab, die wir anschließend testen werden:
H0: μ ≤ 7,2
H1: μ > 7,2
Nun wählen wir anhand der Hypothesen einen geeigneten Test aus. In unserem Fall eignet sich der z-Test am besten, da er überprüft, ob eine Stichprobe aus einer bestimmten Population mit dem Mittelwert μ0 stammt oder nicht. Im Allgemeinen könnte man die Hypothesen des z-Tests folgendermaßen formulieren:
H0: Die Stichprobe stammt aus einer Population, die den Mittelwert μ0 aufweist.
H1: Die Stichprobe stammt nicht aus einer Population, die den Mittelwert μ0 aufweist.
Auch in unserem Beispiel könnte man die Forschungsthesen so formulieren. Die H0 würde in diesem Fall bedeuten, dass der Geschmack unsere Eissorte „Ewiges Eis“ der Population, also allen anderen Eissorten, entspricht und die Abweichung vom Populationsmittelwert von 0,3 Geschmackspunkten daher nur zufällig entstanden ist (H0). Alternativ, könnte man die Abweichung vom Populationsmittelwert von 0,3 Geschmackspunkten dadurch erklären, dass unser Eis wirklich besser Schmeckt, also nicht aus dieser Population stammt bzw. sich signifikant von dieser Population unterschiedet (H1). Das folgende Schaubild zeigt die Situation grafisch.
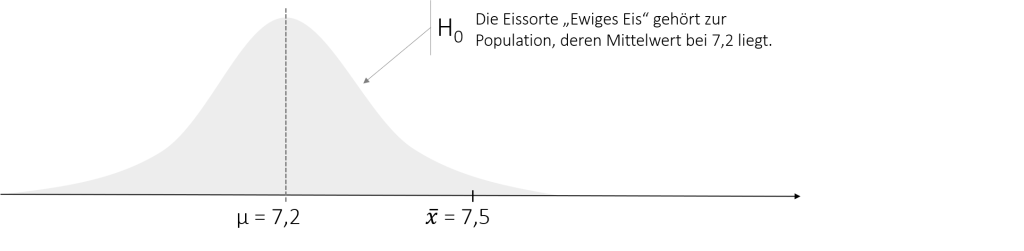
Der grau schattierte Bereich zeigt die Wahrscheinlichkeit der H0 (Später auch P-Wert genannt). Je weiter der gefundene Stichprobenmittelwert vom Populationsmittelwert μ entfernt ist, desto unwahrscheinlicher ist die H0. Die Regel, ab wann diese dann abzulehnen ist, werden wir im folgenden kennen lernen (Die Festlegung dieser Grenze ist der eigentliche Z-Test). Zuvor wollen wir uns abschließend nochmal den möglichen Hypothesen widmen. Grundsätzlich kann der Z-Test ungerichtet, oder links-/rechtsseitig gerichtet durchgeführt werden. Die folgende Tabelle zeigt die daraus resultierenden Hypothesenpaare für unser Beispiel.
| Die Alternativ- hypothese ist… |
H0 | H1 | Beispiel der Alternativ- hypothese |
| ungerichtet | μ = μ0 | μ ≠ μ0 | Unsere Eiscreme-Sorte schmeckt nicht wie die der Konkurrenz und erzielt dementsprechend eine andere Geschmackspunktzahl. |
| gerichtet (rechtsseitig) | μ ≤ μ0 | μ > μ0 | Unsere Eiscreme-Sorte schmeckt besser als das Konkurrenzprodukt und erzielt damit mehr Geschmackspunkte. |
| gerichtet (linksseitig) | μ ≥ μ0 | μ < μ0 | Unsere Eiscreme-Sorte schmeckt schlechter als das Konkurrenzprodukt und erzielt damit weniger Geschmackspunkte. |
μ steht hierbei für den Erwartungswert der Population, aus der wir unsere Stichprobe gezogen haben (in unserem Fall also der Erwartungswert unserer Eiscreme-Sorte „Ewiges Eis“). μ0 hingegen steht für den Populationsparameter, gegen den wir testen (im Beispiel wäre das die 7,2 Geschmackspunkte des Konkurrenten). Dieser wird in den statistischen Hypothesen als fester Wert dargestellt.
11.2 Voraussetzungen prüfen
Zudem müssen wir, bevor wir mit dem Test beginnen, überprüfen, ob unsere Daten die Voraussetzungen des Tests erfüllen. Beispielsweise unterscheiden sich Signifikanztests darin, welches Skalenniveau sie benötigen oder welche Verteilungsfunktion in den Daten vorliegen muss.
Der z-Test besitzt folgende Voraussetzungen:
- Die abhängige Variable muss mindestens intervallskaliert sein.
- Die Daten sollten normalverteilt sein. Jedoch kann ab n > 30, gemäß dem zentralen Grenzwerttheorem, von dieser Voraussetzung abgesehen werden.
- Die Standardabweichung der Population σ (bzw. die Populationsvarianz σ2) muss bekannt sein.
In unserem Beispiel sind alle Voraussetzungen erfüllt, da wir bei den Geschmackspunkten von einer Intervallskala ausgehen, unsere Stichprobe ein n > 30 aufweist und die Populationsvarianz mit σ2 = 0,36 bekannt ist. Nun können wir mit der Testung unserer Hypothesen beginnen.
11.3 Berechnung der Prüfgröße z
Um die Abweichung der Stichprobe von der angenommenen Grundgesamtheit messen zu können, berechnen wir zunächst die Prüfgröße (auch Teststatistik genannt), die sich von Test zu Test unterscheidet. Im Falle des z-Tests berechnen wir die Prüfgröße z. Diese Prüfgröße sollte Ihnen aus dem Kapitel z-Standardisierung bekannt vorkommen. Diese Prüfgröße drückt die Mittelwertsdifferenz zwischen dem gefundenen Mittelwert ![]() und dem Populationsmittelwert μ in Standardfehlern aus. Dadurch überführen wir die Stichprobenkennwerteverteilung aus unserer Aufgabenstellung (in unserem Beispiel eine Normalverteilung mit μ0= 7,2 und σ2 = 0,36) in eine Standardnormalverteilung mit μ= 0 und σ =1. Dieses Vorgehen hat den Vorteil, dass wir nun anhand des berechneten z-Wertes die Auftretenswahrscheinlichkeit für unseren gefundenen Mittelwert aus der Stichprobe mittels Tabellen bestimmen können (aber dazu später mehr).
und dem Populationsmittelwert μ in Standardfehlern aus. Dadurch überführen wir die Stichprobenkennwerteverteilung aus unserer Aufgabenstellung (in unserem Beispiel eine Normalverteilung mit μ0= 7,2 und σ2 = 0,36) in eine Standardnormalverteilung mit μ= 0 und σ =1. Dieses Vorgehen hat den Vorteil, dass wir nun anhand des berechneten z-Wertes die Auftretenswahrscheinlichkeit für unseren gefundenen Mittelwert aus der Stichprobe mittels Tabellen bestimmen können (aber dazu später mehr).
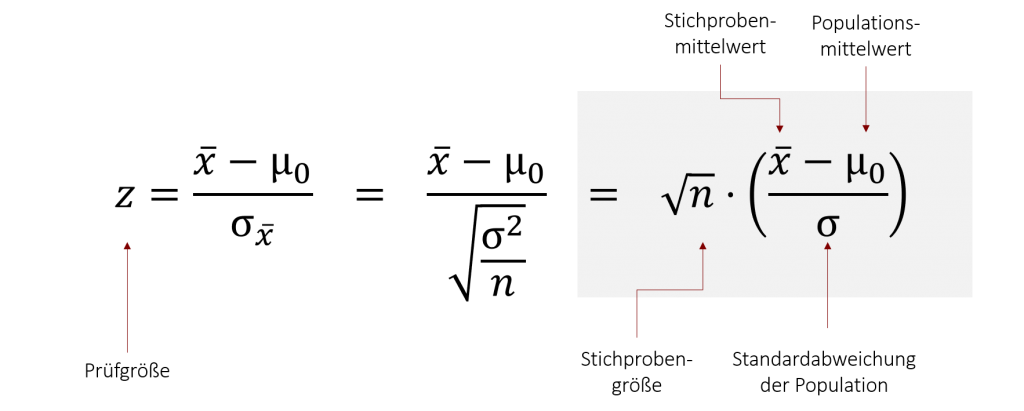
Rechnen wir zunächst die Prüfgröße z für unser Beispiel der Eissorten aus:
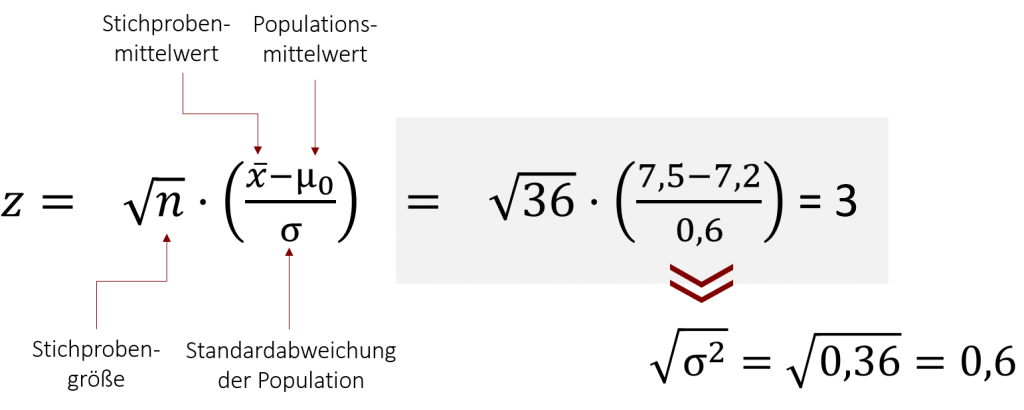
Die Prüfstatistik für unseren Stichprobenmittelwert ist zemp = 3.
An dieser Beispielrechnung wird ein weiterer wichtiger Grundsatz der Hypothesentestung deutlich. Wir berechnen den z-Wert des Stichprobenmittelwerts unter Annahme, dass er zu der Normalverteilung mit μ0= 7,2 und σ = 0,6 gehört. Wenn Sie sich an den vorherigen Absatz der Hypothesenaufstellung erinnern, so war genau dies die Annahme der H0. Dementsprechend prüfen wir, wie wahrscheinlich es ist, dass unsere Daten aus der Stichprobe (hier: 7,5 Geschmackspunkte) auftreten, wenn die H0 gilt.
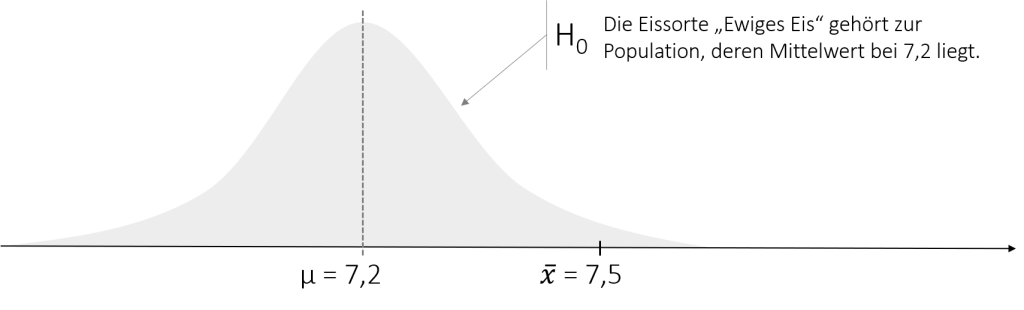
Noch Fragen offen geblieben? Das folgende Video erklärt die Berechnung der Prüfgröße z anhand der Discobeleuchtung in der Five Profs Kette.
11.2 Z-Test Gaußtest | Berechnung der Prüfgröße Z
11.4 Konstruktion des Ablehnungsbereichs und Entscheidung
Im nächsten Schritt des Testens gilt es zu klären, wie wahrscheinlich unser gefundener z-Wert unter Annahme der Nullhypothese ist. Ist sein Auftreten „unwahrscheinlich genug“, können wir die H0 ablehnen. Doch wie definieren wir, welcher z-Wert für uns „unwahrscheinlich genug“ ist? Hierfür konstruieren wir einen Ablehnungsbereich, dessen Grenzen als kritische z-Werte oder kurz zkrit bezeichnet werden. Liegt unser empirisch gefundener z-Wert zemp in diesem Ablehnungsbereich, so wird die H0 abgelehnt und die Alternativhypothese angenommen.
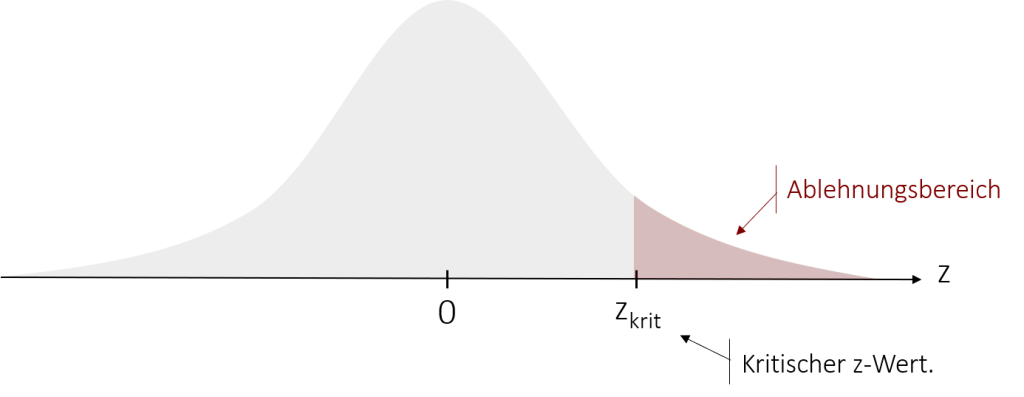
Wo genau unsere kritischen z-Werte liegen, hängt dabei vom Signifikanzniveau α ab, welches wir im Vorhinein definieren. Mit dem Signifikanzniveau legen wir fest, welche Irrtumswahrscheinlichkeit α wir akzeptieren möchten. Zur Wiederholung zeigt Ihnen die folgende Tabelle die üblichen Signifikanzniveaus in der Forschung. Welches Signifikanzniveau Sie dabei festlegen, ist ganz allein Ihnen überlassen, jedoch sollte die Entscheidung unter Berücksichtigung der jeweiligen Forschungshypothese erfolgen.
| α | % | Beschreibung |
| α = 0,1 (.10) | 10%-Signifikanzniveau | marginal signifikant |
| α = 0,05 (.05) | 5%-Signifikanzniveau | signifikant |
| α = 0,01 (.01) | 1%-Signifikanzniveau | hoch signifikant |
| α = 0,001 (.001) | 0,1%-Signifikanzniveau | höchst signifikant |
In unserem Eis-Beispiel wollen wir auf Nummer sicher gehen und legen unser Signifikanzniveau auf 1% fest. Anders gesagt legen wir fest, dass wir uns gegen unsere Nullhypothese („Unser Eis schmeckt gleich oder schlechter als das der Konkurrenz“) entscheiden, wenn die Wahrscheinlichkeit für das Auftreten unseres empirischen z-Werts unter 1% liegt. Graphisch sieht der Ablehnungsbereich für unser Beispiel wie folgt aus:
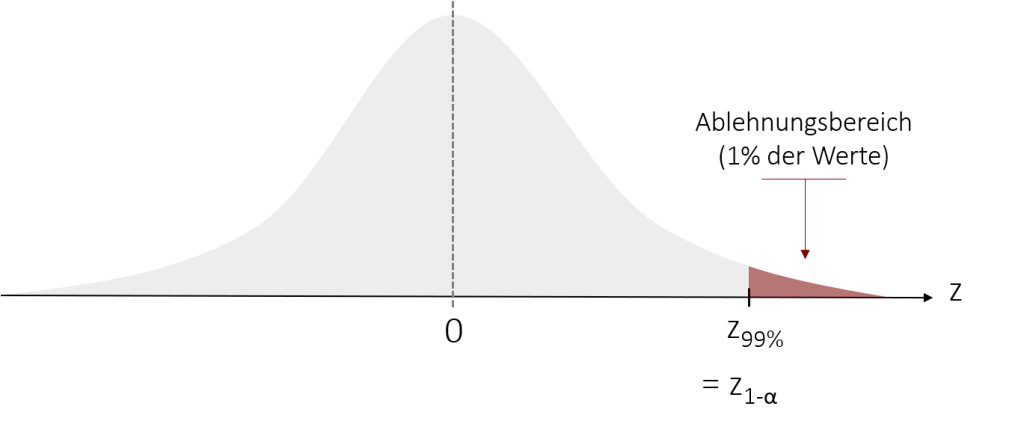
Im definierten Ablehnungsbereich liegen genau 1% der Werte unter der Standardnormalverteilung. Anders gesagt bedeutet dies, dass unter Annahme der H0 bei einer Zufallsziehung nur 1% der Stichproben ein solches Ergebnis liefern würden. Wir bestimmen nun den zugehörigen z-Wert wieder aus einer Tabelle für die Standardnormalverteilung. Da diese Tabellen meist nur die Werte von – unendlich bis zum entsprechenden z-Wert angeben, müssen wir noch den Kehrwert berechnen (1- α) , also 1 – 0,01 = 0,99. Dies definiert die Grenze des Ablehnbereichs zkrit (= z1-α).

Unser kritischer z-Wert hat laut der Tabelle einen Wert von 2,33. Da die Tabellen immer nur grob die Werte angeben, hätten wir alternativ auch den kritischen z-Wert von 2,32 wählen können. Da wir jedoch unsere H0 nicht zu schnell ablehnen möchten, bietet es sich grundsätzlich an, den konservativeren Wert zu wählen. Der Wert 2,33 stellt somit unsere kritische Grenze dar, ab der wir die H0 ablehnen. Diese vergleichen wir nun mit unserer Prüfgröße z. Wenn unsere Prüfgröße größer als der kritische z-Wert ist, liegt sie im Ablehnungsbereich, in der wir die Nullhypothese verwerfen. Da unsere Prüfgröße einen Wert von zemp=3 aufweist und damit größer ist als der kritische z-Wert, lehnen wir die Nullhypothese im vorliegenden Fall ab.
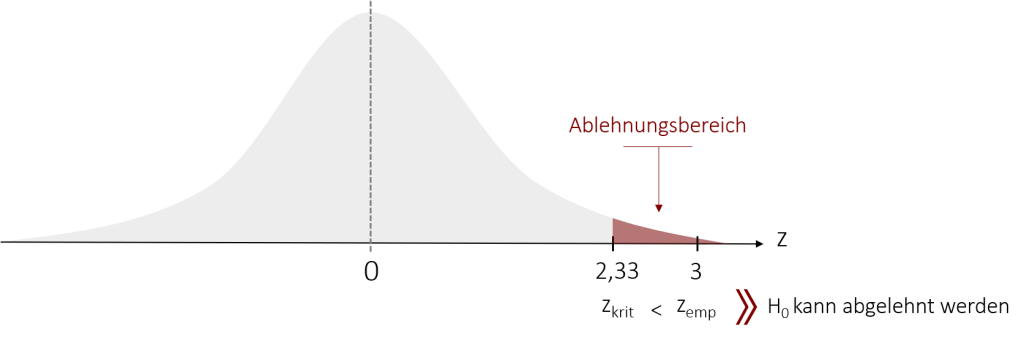
Wir können sagen, dass die Wahrscheinlichkeit, dass unser erhobener Stichprobenmittelwert zur selben Population, wie die Eiscreme-Sorte der Konkurrenz gehört, bei unter 1% liegt. Dadurch wird unser selbstgewähltes Signifikanzniveau unterschritten und man kann von einem signifikanten Unterschied sprechen (bzw. genauer: einem hoch signifikantem Unterschied, da das Signifikanzniveau bei α = 1% lag).
Wenn wir zurück an unsere Aufgabenstellung denken, wollten wir herausfinden, ob unsere Eissorte „Ewiges Eis“, besser beim Geschmackstest abschneidet als die Konkurrenzsorten. Dadurch, dass wir die H0 abgelehnt haben, können wir diese Frage nun beantworten und sagen, dass unsere Eissorte signifikant besser schmeckt, als die Eissorten der Konkurrenz (mit einer Irrtumswahrscheinlichkeit von 1%). Mit dieser Entscheidung ist unser Testverfahren abgeschlossen.

In unserem Beispiel haben wir einen einseitigen z-Test durchgeführt mit einer gerichteten rechtsseitigen Hypothese. Der z-Test kann jedoch auch andere Hypothesenpaare testen, wie z.B. eine gerichtete linksseitige oder eine ungerichtete Hypothese. Um zu verdeutlichen, wie wir den Ablehnungsbereich in diesen Fällen konstruieren, drehen wir unser Beispiel um und prüfen die folgenden Behauptungen:
H0: Die Eiscreme-Sorte „Ewiges Eis“ erzielt die gleiche oder eine höhere Geschmackspunktzahl als das Konkurrenzprodukt. μ ≥ 7,2
H1: Die Eiscreme-Sorte „Ewiges Eis“ erzielt eine niedrigere Geschmackspunktzahl als das Konkurrenzprodukt. μ < 7,2
Bei einem Signifikanzniveau von 1% sieht unser Ablehnungsbereich wie folgt aus:
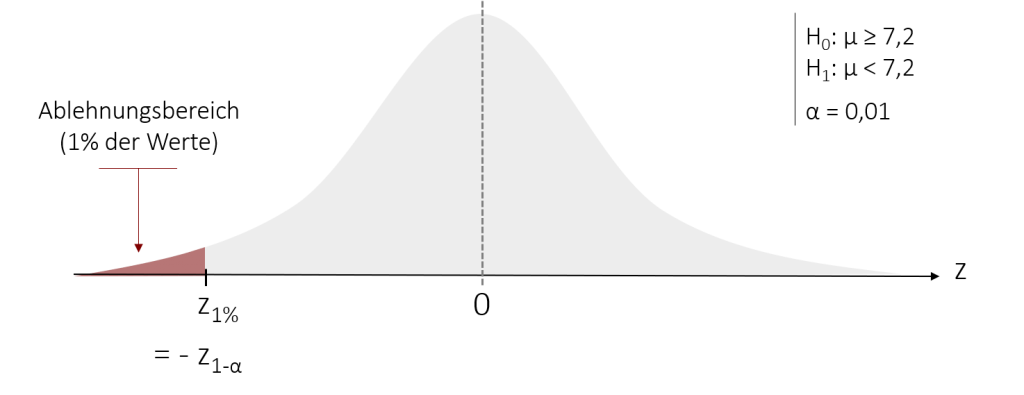
Wir sehen, dass unser Ablehnungsbereich nun auf der anderen Seite der Verteilung liegt. Dies liegt daran, weil wir aufgrund unserer linksseitigen Hypothese vermuten, dass unsere Prüfgröße kleiner als der Erwartungswert der Verteilung ausfällt. Dementsprechend lehnen wir die Nullhypothese ab, wenn unsere Prüfgröße zemp kleiner als der entsprechende kritische z-Wert zkrit ist. Um zu berechnen, wo unser kritischer z-Wert liegt, nutzen wir wieder eine Tabelle für die Standardnormalverteilung, basierend auf unserem festgelegten Signifikanzniveau. Da dieses auf α=1% festgelegt wurde, ist die Grenze unseres Ablehnungsbereichs bei dem z-Wert, bis zu welchem 1% aller Daten liegen. Es gilt:
zkrit = – z(1-α)
Für unseren kritischen Wert von z1% würden wir demnach Folgendes berechnen:
zkrit = – z(1-0,01) = – z0,99 = – 2,33
Wenn unsere Prüfgröße einen kleineren Wert als -2,33 aufweist, so befindet zemp sich im Ablehnungsbereich und wir können die H0 ablehnen. Ist der Teststatistik größer als der kritische z-Wert, wird die H0 beibehalten.
In einem letzten Beispiel schauen wir uns unser Eiscreme-Szenario für eine ungerichtete Hypothese bei einem Signifikanzniveau von 1% an. Unsere Hypothesen lauten hierbei:
H0: Die Eiscreme-Sorte „Ewiges Eis“ schmeckt gleich gut wie die Konkurrenz und erzielt die gleiche Geschmackspunktzahl wie die Konkurrenzprodukte (μ = 7,2).
H1: Unsere Eiscreme-Sorte schmeckt nicht wie die der Konkurrenz und erzielt dementsprechend eine andere Geschmackspunktzahl (μ ≠ 7,2).
In diesem Fall führen wir einen zweiseitigen z-Test durch. Hierfür bilden wir auf beiden Seiten der Verteilung einen Ablehnungsbereich, da wir keine Vermutung darüber aufstellen, auf welcher Seite der Verteilung sich unsere empirisch erhobene Prüfgröße z befindet. Als Konsequenz halbiert sich die Fläche unserer Ablehnungsbereiche auf beiden Seiten, sodass wir nun statt einem Ablehnungsbereich mit 1%, zwei Ablehnungsbereiche mit jeweils 0,5% haben.
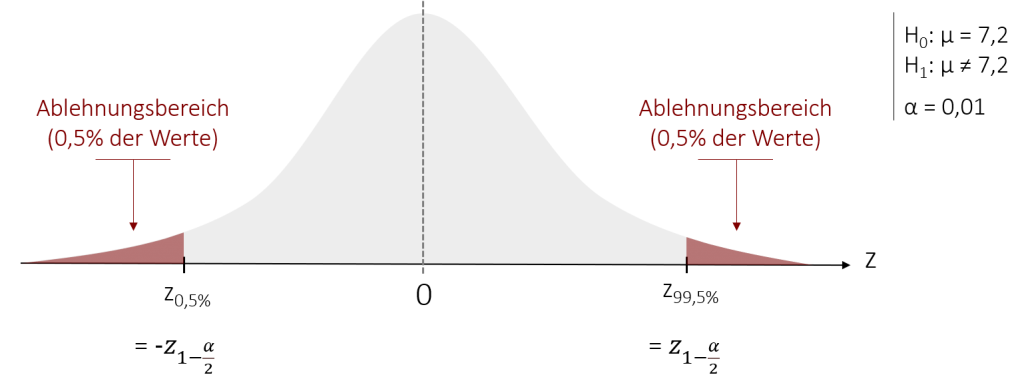
Dementsprechend ändern sich auch unsere kritischen z-Werte, die die Grenzen, der Ablehnungsbereiche bilden. Statt bei z1-α zu liegen, befinden sie sich nun bei +/- z1-α/2. Für unser Beispiel mit einem Signifikanzniveau von 1% liegen sie damit bei:
Untergrenze: zkrit = -z1-α/2 = -z1-0,01/2 = -z0,995 = – 2,58
Obergrenze: zkrit = z1-α/2 = z1-0,01/2 = z0,995 = 2,58
Ist unsere empirische Prüfgröße kleiner als zkrit von -2,58 beziehungsweise größer als unser oberer kritischer z-Wert von +2,58, können wir die Nullhypothese ablehnen und damit bestätigen, dass sich unsere Eiscreme-Sorte „Ewiges Eis“ in der Geschmacksbewertung signifikant von der Konkurrenz unterscheidet (mit einer Fehlerwahrscheinlichkeit von 1%).
Um die Konstruktion des Ablehnungsbereichs und die Entscheidung besser nachvollziehen zu können, zeigt Ihnen das folgende Video von Five Profs eine Beispielrechnung an einem Praxisfall.
11.3 Z-Test Gaußtest | Konstruktion des Ablehnbereichs und Entscheidung
Zudem zeigt Ihnen die folgende Tabelle eine Übersicht, über alle Hypothesenpaare des z-Tests und wie die entsprechenden Zwischenschritte zu berechnen sind.
Voraussetzungen : Intervalldaten; für n < 30 Normalverteilung in den Daten, ab n ≥ 30 beliebige Verteilung; σ bekannt
| Hypothesen | H0: μ = μ0
H1: μ ≠ μ0 |
H0: μ ≤ μ0
H1: μ > μ0 |
H0: μ ≥ μ0
H1: μ < μ0 |
| Bestimmung der Prüfgröße (zemp) | |||
| Bestimmung kritischer z-Wert (zkrit) | zkrit = -z1-α/2 ; + z1-α/2 | zkrit = z1-α | zkrit = – z1-α |
| H0 ablehnen, wenn: | |zemp| > z1-α/2 | zemp > zkrit | zemp < zkrit |
Rechenbeispiel Z-Test
Wir haben die Vermutung, dass die Einführung des neuen interaktiven Skripts die Lernleistung in Statistik, gemessen über das Abschneiden in der Klausur, verbessert. Um diese Hypothese zu überprüfen, ziehen wir eine Zufalls-Stichprobe von n=45 Studierenden, die das neue interaktive Skript erhalten. Diese haben einen Durchschnitt von = 82 Punkten in der Klausur (von 100 möglichen Punkten). Bei Studierenden, die kein interaktives Skript hatten, lag der langjährige Populationsmittelwert in der Klausur bei μ0 = 80 mit σ2=64 (bzw. σ=8). Unser festgelegtes Signifikanzniveau beträgt 5%.
Hypothesen aufstellen:
H0: μ ≤ 80
(Studierende mit interaktivem Skript erzielen in der Klausur die gleiche oder eine geringere Punktzahl, als Studierende ohne ein interaktives Skript)
H1: μ > 80
(Studierende mit interaktivem Skript erzielen in der Klausur eine höhere Punktzahl, als Studierende ohne ein interaktives Skript mit einem μ0 = 80)
Voraussetzungen prüfen: Intervalldaten (✓); n > 30, sodass Verteilung beliebig ist (✓); σ gegeben (✓)
Prüfgröße berechnen:![]()
kritischen z-Wert berechnen: zkrit = z1-α = z0,95 = 1,65
Entscheidung treffen: zemp > zkrit –> H0 ablehnen
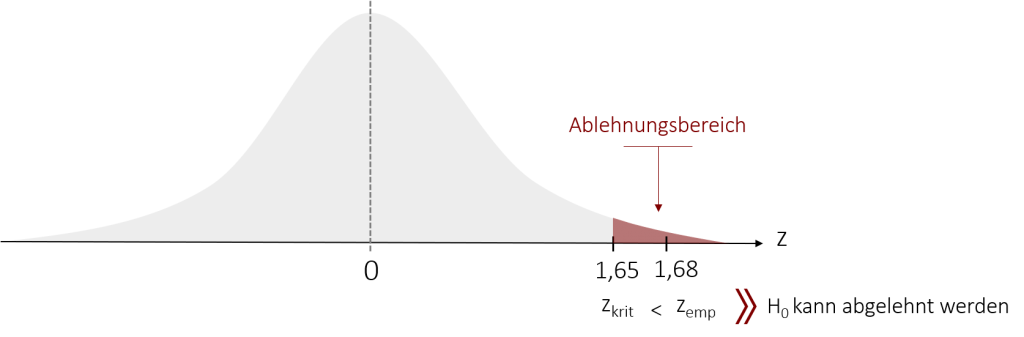
- Antwort:
Aufgrund der Untersuchung kann angenommen werden, dass das interaktive Skript die Lernleistung der Studierenden verbessert hat (mit einer Fehlerwahrscheinlichkeit von 5%).
11.5 p-Wert als Entscheidungskriterium
Um zu entscheiden, ob wir die H0 ablehnen oder beibehalten, haben wir im vorausgegangenen Absatz die Prüfgröße zemp mit dem kritischen z-Wert zkrit verglichen. Als Alternative kann man stattdessen auch den p-Wert als Entscheidungskriterium verwenden, welcher in der Praxis deutlich häufiger angegeben wird.
Hierfür berechnen wir aus unserer Prüfgröße z einen p-Wert, welcher die Wahrscheinlichkeit für die H0 ausdrückt. Oder anders ausgedrückt: Die Wahrscheinlichkeit, dass wir solch einen Stichprobenmittelwert und damit empirischen z-Wert erhalten, unter der Annahme der H0. Beispielsweise würde ein p-Wert von 1,75% aussagen, dass das Auftreten unseres empirischen z-Werts unter Annahme der Nullhypothese eine Wahrscheinlichkeit von 1,75% besitzt. Um anschließend zu entscheiden, ob wir die H0 ablehnen oder beibehalten, vergleichen wir diesen p-Wert mit unserem im Vorhinein bestimmten Signifikanzniveau α. Wenn der p-Wert kleiner als unser definiertes Signifikanzniveau α ist, dann können wir die H0 verwerfen. In unserem Beispiel wählen wir ein 5%-Signifikanzniveau. Da unser p=1,75% kleiner als α=5% ist, entscheiden wir uns in diesem Fall für eine Ablehnung der Nullhypothese. Unsere Begründung hierbei ist, dass unser z-Wert lediglich mit einer Wahrscheinlichkeit von 1,75% unter Annahme der Nullhypothese auftritt, sodass das Ergebnis besser mit der Alternativhypothese zu vereinbaren wäre.
Doch schauen wir uns dieses Vorgehen einmal Schritt für Schritt an unserem Eiscreme-Beispiel an. Die Hypothesenaufstellung, Prüfung der Voraussetzungen des Tests, sowie die Berechnung der Prüfstatistik z bleiben gleich. Erst nach diesen Schritten berechnen wir den p-Wert. Zur Erinnerung, unsere Hypothesen lauten hierbei:
H0: Die Eiscreme-Sorte „Ewiges Eis“ erzielt die gleiche oder eine schlechtere Geschmackspunktzahl als die Konkurrenzprodukte.
H1: Die Eiscreme-Sorte „Ewiges Eis“ erzielt eine höhere Geschmackspunktzahl als die Konkurrenzprodukte.
Für unseren Stichprobenmittelwert von =7,5 Geschmackspunkten haben wir daraufhin eine Prüfgröße von zemp= 3 berechnet. Für diese Prüfgröße gilt es nun, einen p-Wert zu berechnen.
1. Schritt: Berechnung des p-Werts
Um den p-Wert zu ermitteln, berechnen wir die Fläche, die der empirische z-Wert (in unserem Beispiel: zemp= 3) an den (interessierenden) Enden der Prüfverteilung abschneidet. Graphisch sieht diese Fläche wie folgt aus:
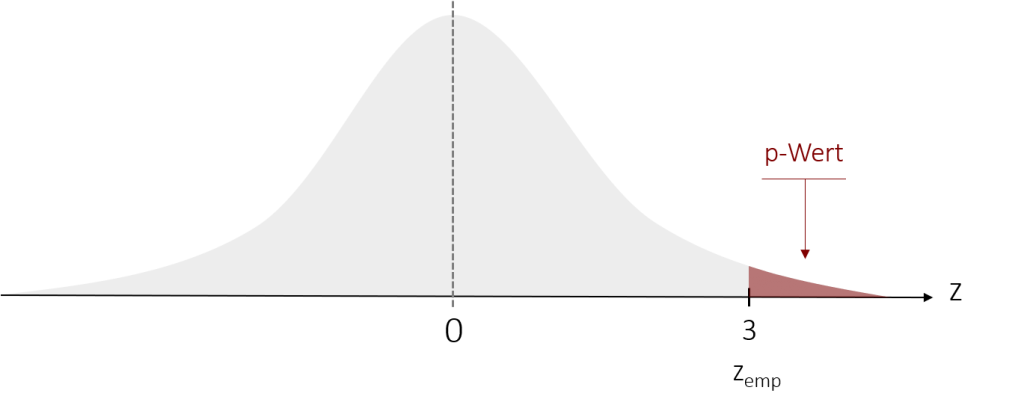
Zur Berechnung dieses p-Werts benutzen wir wieder unsere Tabellen. In ihnen sehen wir, wie wahrscheinlich es ist, dass ein bestimmter oder kleinerer z-Wert auftritt. Für unseren empirischen z-Wert von 3 ermitteln wir so eine Wahrscheinlichkeit von Φ(3) = 99,865%. Das ist jedoch die Wahrscheinlichkeit für die Fläche von – bis zu unserem z-Wert. Der p-Wert hingegen beschreibt die Fläche am Ende unserer Prüfverteilung. Aus diesem Grund berechnet sich unser p-Wert aus dem Kehrwert dessen:
p = 1 – Φ(3) = 1 – 0,99865 = 0,00135 ≡ 0,135%
Die Wahrscheinlichkeit für die H0 beträgt somit 0,135%.
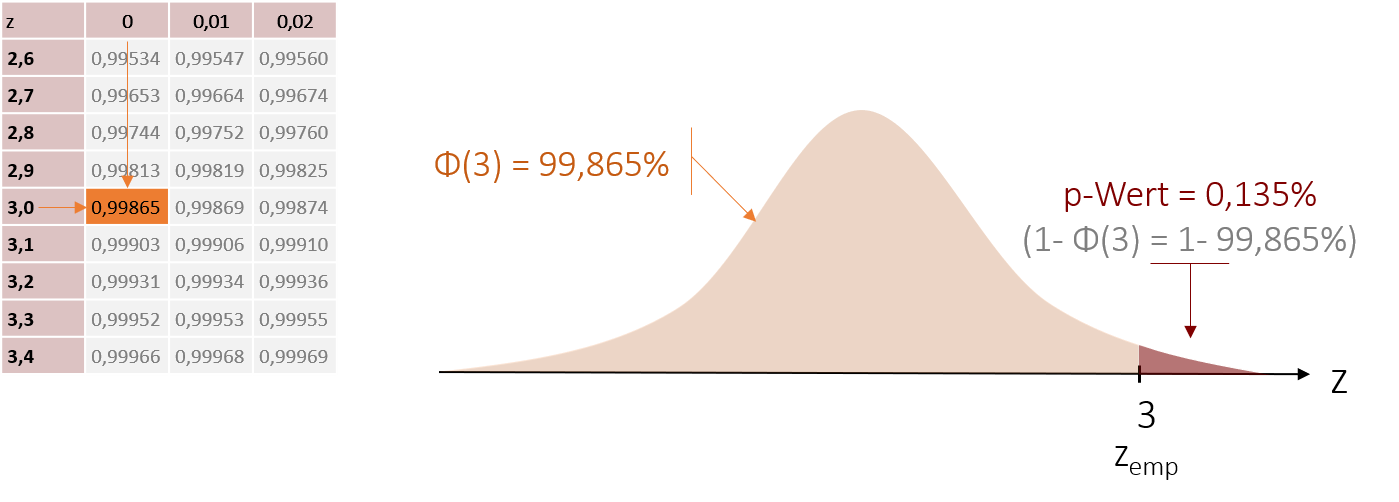
Unser Beispiel beschreibt die Berechnung des p-Werts an einer rechtsseitig gerichteten Hypothese. Für die beiden anderen möglichen Hypothesenpaare des z-Tests wird der p-Wert folgendermaßen berechnet:
| Alternativ- hypothese ist: |
Hypothesenpaar | Berechnung des p-Werts | |
| gerichtet (rechtsseitig) unser Beispiel |
H0: μ ≤ μ0
H1: μ > μ0 |
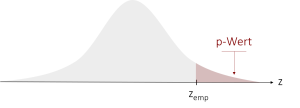 |
p = 1 – Φ(zemp) |
| gerichtet (linksseitig) | H0: μ ≥ μ0
H1: μ < μ0 |
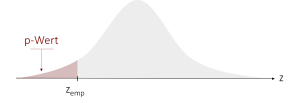 |
p = Φ(zemp) |
| ungerichtet | H0: μ = μ0
H1: μ ≠ μ0 |
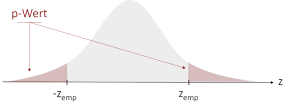 |
p = Φ(zemp) * 2 |
Wir sehen, dass sich bei einer ungerichteten Hypothese der p-Wert verdoppelt. Dies passiert, da er an beiden Enden der Prüfverteilung auftritt.
2. Schritt: Entscheidung
Für die Entscheidung, ob wir die H0 auf Basis unserer Daten ablehnen, vergleichen wir, wie schon erwähnt, nicht den zemp mit dem zkrit, sondern diesmal den p-Wert (der zu unserem zemp gehört) mit dem vordefinierten Signifikanzniveau α. Die alternative Entscheidungsregeln lautet hierbei:
| p < α | Ablehnung der H0 |
| p > α | H0 kann nicht abgelehnt werden, (keine Aussage möglich) |
Zur Gegenüberstellung der beiden Herangehensweisen bei der Entscheidung soll Ihnen die folgende Grafik dienen. Man sieht, dass bei der Entscheidung mit dem p-Wert die beiden Flächen verglichen werden und nicht die z-Werte.
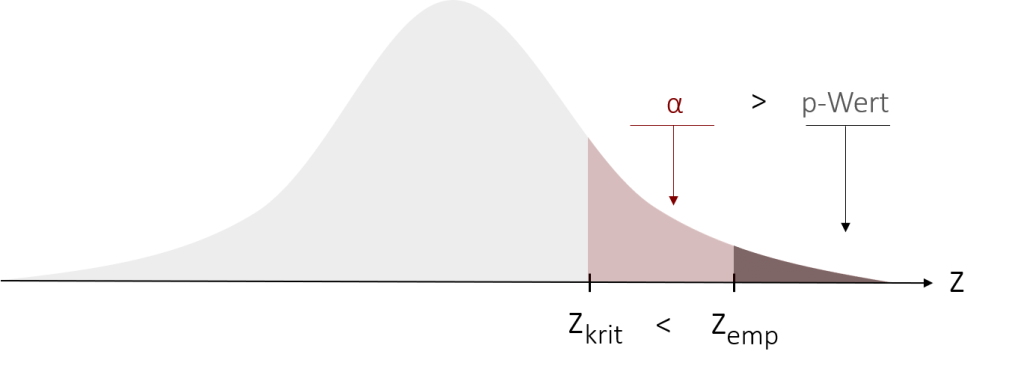
Grundsätzlich sind beide Wege gleichberechtigt und eigentlich auch zwei Seiten der gleichen Medaille. Da die Prüfgröße bei jedem Test unterschiedlich ist (nach dem z-Test werden Sie noch den T-Test, den F-Test und viele mehr kennen lernen), ist in der Praxis meist der P-Wert für die Interpretation beliebter. Dieser ist bei jedem Test gleichermaßen und auch ohne Tabelle interpretierbar. Es gilt bei jedem Test grundsätzlich: Ist der P-Wert kleiner als das Signifikanzniveau, kann die H0 verworfen werden.
Beispiel Interpretation über P-Wert
Wir möchten die Hypothese testen, dass die FiveProfs-YouTube Abonnenten schlauer sind als die Durchschnittsbevölkerung. Aus diesem Grund führen wir ein Intelligenztest bei n = 45 Abonnenten durch, in dem eine Mittelwert von 105 IQ Punkten herauskommt. Durch die Normierung der IQ- Punkte ist bekannt, dass der Durchschnitt einen IQ von μ=100 und dabei eine Standardabweichung von σ=15 IQ-Punkten besitzt. Sind unsere Abonnenten nun signifikant schlauer (α = 5%)?
Hypothesen aufstellen:
H0: μ ≤ 100
H1: μ > 100
Voraussetzungen prüfen: Intervalldaten (✓); n > 30, sodass Verteilung beliebig ist (✓); σ gegeben (✓)
Prüfgröße berechnen:![]()
p-Wert berechnen: p = 1- Φ(2,24) = 1 – 0,9875 = 0,0125
Entscheidung treffen: p=0,0125 < α=0,05 –> H0 ablehnen
Antwort: Die FiveProfs-Abonnenten sind signifikant schlauer als die Durchschnittsbevölkerung bei einer Fehlerwahrscheinlichkeit von 5%.
Das folgende Video von Five Profs veranschaulicht und erklärt Ihnen das Thema nochmals an einem Beispiel
11.4 Z-Test Gaußtest | P-Wert und Interpretation
Doch was bedeutet ein signifikanter Unterschied eigentlich?
11.6 Aussagekraft des Signifikanztests
Um zu ergründen, was für eine Aussagekraft ein signifikantes Ergebnis besitzt, müssen wir uns die Logik von Signifikanztests nochmal vor Augen führen. Ein Signifikanztest ermittelt die Wahrscheinlichkeit eines Ergebnisses bei Gültigkeit der Nullhypothese: P(Ergebnis | H0). Wir machen also nur Aussagen über die Wahrscheinlichkeit der Daten unter der Annahme der Nullhypothese. Wenn wir dementsprechend ein signifikantes Ergebnis erhalten, muss die Nullhypothese (die wir ablehnen) nicht zwangsweise falsch sein. Die gefundenen Daten sind nur recht unwahrscheinlich unter Annahme der Nullhypothese. Zum Vergleich: wenn wir bei einem nicht signifikanten Ergebnis die H0 beibehalten, muss auch diese nicht zwangsweise richtig sein. Unsere gefundenen Daten sind nur nicht unwahrscheinlich genug, als dass wie die Nullhypothese ablehnen können.
Lassen Sie uns das eben Gesagte nochmal an einem Beispiel verdeutlichen. Nehmen wir an, wir haben durch eine Stichprobe herausgefunden, dass die FiveProfs-Abonnenten einen signifikant höheren IQ von 105 IQ-Punkten aufweisen als die Durchschnittsbevölkerung mit 100 IQ-Punkten (α = 5%). Als wir den z-Test durchgeführt haben, konnten wir aus diesem Grund die Nullhypothese ablehnen. Die Bedeutung dieses Ergebnisses lässt sich wie folgt zusammenfassen:
„Die Wahrscheinlichkeit für unser Messergebnis von durchschnittlich 105 IQ-Punkten bei 45 Abonnenten unter der Annahme, dass sie zu einer Population gehören, deren Mittelwert bei 100 IQ-Punkten liegt, beträgt weniger als 5% und ist damit relativ unwahrscheinlich.“
Was wir hingegen nicht durch unser signifikantes Ergebnis schlussfolgern können, ist, welche Wahrscheinlichkeit die Null- oder Alternativhypothese besitzen. Wir können also nichts über P(H0 | Ergebnis) oder P(H1 | Ergebnis) aussagen. Die folgende Behauptung wäre damit falsch:
„Die Wahrscheinlichkeit, dass unsere Abonnenten schlauer sind als die Durchschnittsbevölkerung beträgt 95%.“
11.7 Statistische vs. praktische Signifikanz (Bedeutsamkeit)
Wenn ein Effekt statistisch signifikant ist, wird ihm meist auch eine praktische Bedeutsamkeit zugesprochen. Dies ist aber nicht unbedingt gegeben, da ein Signifikanztest nicht nur eher „ausschlägt“, je größer ein Effekt und je größer das Signifikanzniveau α ist, sondern auch je sensitiver der gewählte Test und je größer die Stichprobengröße ist. Das bedeutet, dass selbst kleinste Effekte (wie z.B. geringe Mittelwertsunterschiede) bei sensitiven Tests mit einer großen Stichprobengröße signifikant werden können. Denn je größer die Stichprobe ist, desto genauer ist auch die Messung und umso eher können wir uns sicher sein, dass ein Unterschied nicht zufällig ist (bzw. unter Annahme der Nullhypothese zustande gekommen ist). Dadurch ist es möglich, signifikante Unterschiede zu erhalten, die in die Praxis keine Bedeutung haben, wie Ihnen das folgende Beispiel zeigt.
In einer Studie wurde ein neues Fiebermittel getestet und ergab, dass es das Fieber signifikant herabsenken konnte – und zwar um 0,25°C. Die statistische Signifikanz ist in diesem Beispiel zwar gegeben, aber praktisch betrachtet hilft Patienten eine Senkung des Fiebers um 0,25°C leider nur wenig.
Die Ursache der Diskrepanz zwischen statistischer und praktischer Signifikanz liegt darin, dass Signifikanztests nichts über die Größe unserer gefundenen Effekte aussagen. Hierfür benötigen wir ein zusätzliches Maß: die Effektgröße.
11.8 Effektgröße
Die Effektgröße (auch Effektstärke genannt) ist ein standardisiertes Maß, welche die Größe eines gefundenen Effekts (z.B. Mittelwertsunterschied zwischen Testgruppen, Zusammenhang zwischen zwei Variablen) in standardisierter Form angibt. Durch diese Standardisierung sind Effektgrößen zwischen unterschiedlichen Studien oder Maßen vergleichbar. Zudem können wir durch sie unsere erhaltenen Testergebnisse im Hinblick auf ihren Nutzen interpretieren, da die Signifikanz allein nichts über den praktischen Wert unserer Ergebnisse aussagt. Durch die große Bandbreite von Hypothesen existieren in der Statistik unterschiedliche Effektgrößen, die je nach Studiendesign variieren. Beispielsweise gibt es andere Effektgrößen für Zusammenhangs- und für Unterschiedshypothesen, welche wir z.B. beim z-Test prüfen. Auch die gewählten Tests spielen bei der Wahl der passenden Effektgröße eine Rolle. Parametrische Tests, basierend auf metrischen Variablen, besitzen andere Effektgrößen als nicht-parametrische Tests, welche auf nominalen oder ordinalen Variablen basieren. Bei der Berechnung der unterschiedlichen Effektgrößen können an dieser Stelle Statistik-Programme wie G-Power behilflich sein.
Effektgrößen für parametrische Tests (z.B. Z-Test)
Cohen’s d (δ)
Bei Signifikanztests zu Mittelwertsunterschieden, wie beispielsweise beim z-Test, bildet Cohen’s d das gängigste Maß zur Angabe der Effektstärke. Seine Berechnung entspricht der einer z-Standardisierung und baut sich wie folgt auf:

Expertenwissen: Effektgrößen für T-Test
In der allgemeinen Formel wird angenommen, dass die Standardabweichungen von nur einer Population betrachtet werden. Für Tests, bei denen unterschiedliche Populationen berücksichtigt werden (z.B. T-Test), verwendet man die gepoolte Standardabweichung, die die Wurzel aus dem Mittelwert beider Varianzen darstellt.

Als Ergebnis erhalten wir eine Zahl für Cohen’s d, die sich von – bis + erstrecken kann. Diese stellt den Mittelwertsunterschied bezogen auf die (gepoolte) Standardabweichung dar. Eine Effektstärke von .50 bedeutet demzufolge, dass die Differenz zwischen beiden Gruppen gleich einer halben Standardabweichung entspricht. Je größer dabei der Betrag von Cohen’s d, desto größer ist der Effekt. Die Faustregel zur Interpretation der berechneten Effektstärken definiert Cohen (1988) wie folgt:
| |d| = 0,2 | kleiner Effekt |
| |d| = 0,5 | mittlerer Effekt |
| |d| = 0,8 | großer Effekt |
Wie die Berechnung und Interpretation von Cohen’s d im Falle eines z-Tests aussieht, veranschaulicht Ihnen das folgende Video von Five Profs noch einmal genauer.
Video 11.5 Z-Test Gaußtest | Die Effektgröße
Expertenwissen: Weitere Effektgrößen
Weitere Effektgrößen für parametrische Tests
- Pearsons r (ρ)
Den Pearson Korrelationskoeffizienten r haben Sie bereits in Verbindung mit Zusammenhangshypothesen kennengelernt. Er ist ein Maß für den linearen Zusammenhang zweier Variablen und gibt dabei sowohl die Richtung als auch die Stärke des Zusammenhangs an. Sein Wertebereich ist im Gegensatz zu Cohen’s d auf den Bereich zwischen -1 und +1 beschränkt. - Eta Quadrat (η²)
Diese Effektgröße wird bei ANOVAs (Analyse of Variance) verwendet und drückt den gesamten Anteil der durch alle Effekte erklärten Varianz an der Gesamtvarianz aus. Jedoch hat Eta Quadrat einen positiven Bias, sodass die aufgeklärte Varianz immer überschätzt wird. - Omega Quadrat (ω2)
Diese Effektgröße wird ebenfalls bei ANOVAs verwendet und schätzt die aufgeklärte Varianz einer bestimmten Variablen, nachdem die Einflüsse aller anderen Faktoren in der Gesamtvariabilität kontrolliert wurden. Hierbei bezieht es die Anzahl der Gruppen bei der Berechnung der Varianzaufklärung mit ein, sodass es einen geringeren Bias als für die ANOVA hauptsächlich verwendete Effektstärke „partielles Eta Quadrat“ besitzt.
Effektgrößen für nicht-parametrische Tests
- Cohen’s w / Cramers Phi / Cramers V
Alle drei Kennzahlen stellen Effektgrößen in Bezug auf (relative) Häufigkeiten dar und können uns Auskunft über den statistischen Zusammenhang zwischen zwei oder mehreren nominalskalierten Variablen geben. Ihre Berechnung basiert auf einer χ2-Verteilung und damit auf den Abweichungen der beobachteten Häufigkeiten von den erwarteten Häufigkeiten. - Quotenverhältnis (odds-ratio)
Diese Effektgröße ist ebenso wie Cohen’s w / Cramers Phi / Cramers V für Kreuztabellen geeignet, jedoch basiert sie nicht auf (relativen) Häufigkeiten, sondern wie der Name schon sagt, auf Quoten. Das Quotenverhältnis beschreibt dabei ebenfalls den Zusammenhang von zwei Merkmalen und wird durch den Vergleich zweier Quoten berechnet.
11.9 Kritik am Signifikanztest
Der Signifikanztest ist sehr beliebt, weil er ein formales (und scheinbar objektives) Entscheidungskriterium liefert. Der Hypothesentest ist jedoch immer wieder auch in der Kritik, da dieser oft ohne spezifische H1 und mit oftmals unplausibler H0 durchgeführt wird[1]. Ein weiterer Kritikpunkt ist das, meist willkürlich gewählte, Signifikanzniveau.
„Und warum lehren Universitäten und Hochschulen weiterhin den Schwellenwert des P-Wertes von fünf Prozent? Ronald Wasserstein und Nicole Lazar von der American Statistical Association geben die Antwort: Weil dieser Schwellenwert nach wie vor von den meisten Forschern benutzt wird. Und warum benutzen Forscher weiterhin den Schwellenwert? Weil das an den Universitäten gelehrt wird.“ [2]
Aus diesen Gründen sollten bei der Testanwendung oder der Lektüre von Testergebnissen folgende Punkte berücksichtigt und diskutiert werden:
- Ist die H0 plausibel oder a priori falsch?
- Lässt sich die Alternativhypothese präzisieren?
- Welches Signifikanzniveau ist im vorliegenden Fall angemessen?
- Wie groß sollte der Effekt sein (Signifikanz ≠ Bedeutsamkeit)?
11.10 Übungsfragen
Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!
In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!
11.11 Übungsaufgaben
Übungsaufgabe Z-Test
Die Mitarbeiter der Burgerkette Five Profs müssen täglich mehrere tausend Burger zubereiten. Es wird eine Zufallsstichprobe (n = 72) aus der Belegschaft (N = 5.000) gezogen. Die 72 Mitarbeiterinnen und Mitarbeiter bekommen ein exklusives Training vom Burger-Profi Patty, um schneller Burger zu braten. Nach dem Training schaffen die 72 Teilnehmer im Durchschnitt 49 Burger pro Person. Es ist bekannt, dass unsere Mitarbeiter (=Population) im Mittel 47 Burger schaffen, bei einer Varianz von 9.
Können wir nun sagen, dass das Training bei Burger-Profi Patty zu einer signifikanten Veränderung der Mitarbeiterleistung geführt hat? Berechnen Sie hierzu den Z-Wert und interpretieren Sie diesen Anhand der Z-Werte-Tabelle im Anhang.
Die Lösung finden Sie im folgenden Video:
Übungsaufgabe Effektgröße
Berechnen Sie für das Beispiel oben die Effektstärke Cohens‘ d.
Die Lösung finden Sie im folgenden Video:
- Vgl. Woolston, Chris: Psychology journal bans p-values, in: Nature News & Comment, 26.02.2015, [online] https://www.nature.com/news/psychology-journal-bans-p-values-1.17001 [12.12.2020]. ↵
- Vgl. Amrhein, Amrhein: Das magische P, in: Süddeutsche.de, 23.09.2017, [online] https://www.sueddeutsche.de/wissen/wissenschaft-das-magische-p-1.3676252 [12.12.2020]. ↵

 = 4,5 Geschmackspunkten ergeben. Doch reicht dieses Ergebnis aus um nun sagen zu können, dass die neue Cola-Sorte auch wirklich signifikant besser schmeckt als die bisherige? Mit anderen Worten: ist dieser Unterschied auch in der Population so zu erwarten?
= 4,5 Geschmackspunkten ergeben. Doch reicht dieses Ergebnis aus um nun sagen zu können, dass die neue Cola-Sorte auch wirklich signifikant besser schmeckt als die bisherige? Mit anderen Worten: ist dieser Unterschied auch in der Population so zu erwarten? bis zu unserem z-Wert. Der p-Wert hingegen beschreibt die Fläche am Ende unserer Prüfverteilung. Aus diesem Grund berechnet sich unser p-Wert aus dem Kehrwert dessen:
bis zu unserem z-Wert. Der p-Wert hingegen beschreibt die Fläche am Ende unserer Prüfverteilung. Aus diesem Grund berechnet sich unser p-Wert aus dem Kehrwert dessen:
