Hypothesentests
15 T-Tests
15.0 Einleitung t-Tests
Der t-Test widmet sich, wie auch schon der Rangsummen-Test, den Sie im letzten Kapitel kennengelernt haben, der Testung von Unterschiedshypothesen. Er überprüft hierbei, ob ein Unterschied zwischen zwei Gruppen hinsichtlich einer intervallskalierten Variable besteht. Damit lassen sich Fragestellungen beantworten, wie: „Erziele ich mit rötlichem Licht in meiner Burgerfilialer mehr Umsatz als mit Natürlichem?“ oder „Sind Kunden nach dem Verzehr eines FiveProf-Burgers bereit mehr Geld für ein Softdrink auszugeben als vor dem Verzehr?“. Der entscheidende Unterschied gegenüber dem Rangsummen-Test ist die Voraussetzung, dass die abhängige Variable metrisch skaliert sein muss. So untersuchen die eben genannten Fragestellungen, ob ein Unterschied im Umsatz oder in der Zahlungsbereitschaft [in €] vorliegt, anstatt einen Unterschied im Glücksempfinden zu erfassen, der mit Hilfe einer 3er-Skala abgefragt wurde (also ordinal skaliert ist). Die (ungerichteten) Hypothesen, die mittels des t-Tests überprüft werden, lauten somit:
H0: Es gibt keinen Unterschied zwischen den beiden Testgruppen
H1: Es gibt einen Unterschied zwischen den beiden Testgruppen.
Um zu veranschaulichen, wie wir mittels des t-Tests diese Hypothesen überprüfen können, bedienen wir uns eines Beispiels aus der FiveProfs-Burgerkette. Stellen Sie sich vor, wir möchten unsere Kunden zum Verweilen in unseren Filialen bewegen und kaufen aus diesem Grund Sofas der Klasse „Comfort-Luxe“. Nun möchten wir herausfinden, ob unsere Maßnahme Wirkung zeigt und vergleichen die durchschnittliche Besuchszeit unserer Comfort-Filiale mit einer Kontroll-Filiale ohne „Comfort-Luxe“ Sofas. Als Erstes berechnen wir die mittlere Besuchszeit einer zufälligen Stichprobe aus jeder Filiale. In der Filiale mit den Comfort-Sofas beträgt die Besuchszeit durchschnittlich 1= 20 min und in der Kontroll-Filiale 2= 14 min. Wir sehen nun also deskriptiv, dass die Verweilzeit in der Filiale mit den neuen Sofas länger ist. Um jedoch sicher zu sein, dass dieser Effekt auch in der Population so zu erwarten ist (also bei all unseren Filialen und nicht nur bei der kleinen Stichprobe), rechnen wir den t-Test. Dieser sagt uns wie wahrscheinlich es ist, einen solchen Unterschied von 6 Minuten in der Verweildauer zu finden unter der Annahme, dass es in der Population gar keinen Unterschied gibt. Wir ermitteln also die Wahrscheinlichkeit für das Auftreten einer solchen (oder größeren) Mittelwertsdifferenz, unter der Annahme der Nullhypothese. Um hierbei die Wahrscheinlichkeit der Differenz einzuschätzen, wird der Standardfehler als Maßstab verwendet. Ist die Wahrscheinlichkeit für das Auftreten der Differenz (in unserem Fall der 6 minütige Unterschied) gering genug, können wir unsere Nullhypothese verwerfen und einen signifikanten Unterschied zwischen beiden Filialen unterstellen. Anders gesagt können wir also sagen, dass es sehr unwahrscheinlich ist, dass das gefundene Ergebnis nur zufällig entstanden ist und sprechen daher von einem signifikanten (also statistisch bedeutsamen) Ergebnis.
Noch Fragen offen geblieben? Das folgende Video verdeutlicht Ihnen das Vorgehen des t-Tests an einem weiteren Beispiel aus der FiveProfs-Kette.
15.1 Die t-Verteilung
Wie die Kapitelüberschrift schon andeutet, gibt es nicht nur einen t-Test, sondern eine ganze Reihe von t-Tests, die Unterschiedshypothesen überprüfen. Allen gemein ist die Tatsache, dass Sie auf der sogenannten t-Verteilung beruhen ( auch Studentsche t-Verteilung genannt[1]). Doch was genau ist die t-Verteilung und wie unterscheidet sie sich von den anderen kennengelernten Verteilungen?
Anders als bei der bereits kennengelernten z-Verteilung gibt es nicht die eine t-Verteilung. Vielmehr beschreibt die t-Verteilung eine Schar von Verteilungen, die abhängig von den Freiheitsgraden in ihrer Form variiert.
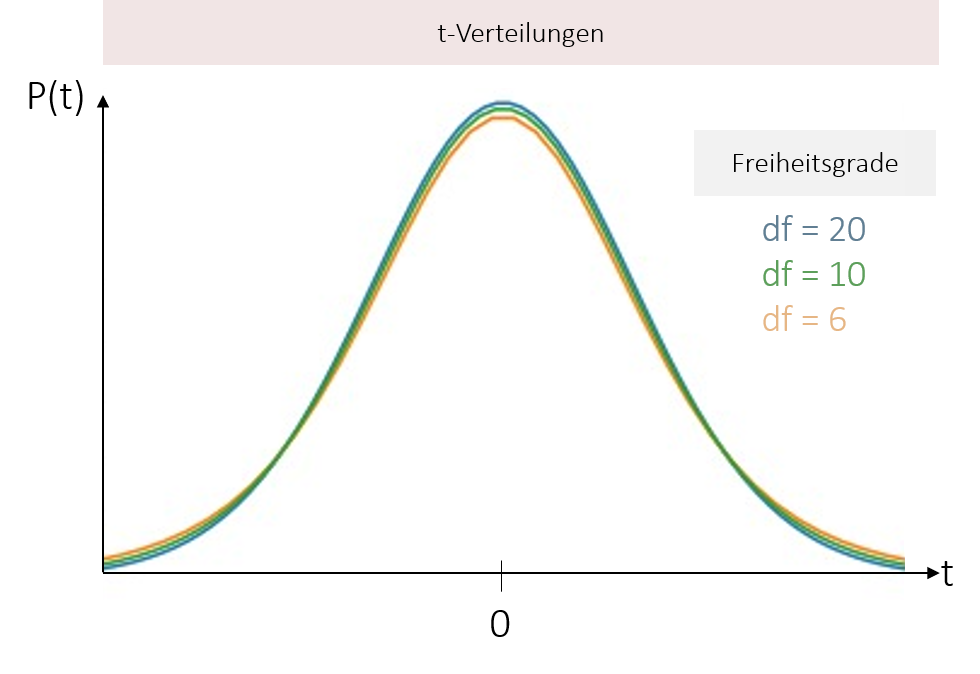
Je größer hierbei die Anzahl der Freiheitsgrade, desto stärker nähert sich die t-Verteilung an die Standardnormalverteilung an. Ab einem n ≥ 30 kann man sie aus diesem Grund konventionsgemäß in eine Standardnormalverteilung approximieren (= überführen). Für balancierte Designs, spricht wenn beide Stichproben gleich groß sind, berechnen sich die Freiheitsgrade (hierbei df) relativ einfach durch die nachfolge Formel. Prüft man hingegen einen Unterschied zwischen unterschiedlichen Gruppengrößen, wird die Formel der Freiheitsgrade deutlich komplizierter. Jedoch rechnen die geläufigen Statistikprogramme wie SPSS die Freiheitsgrade automatisch aus, sodass wir den zweiten Fall hier nicht weiter vertiefen.

15.2 Arten von t-Tests
Grundsätzlich gibt es drei Mögliche Anwendungsfälle von Tests für Mittelwertsunterschiede für die jeweils eine andere Variante des t-Tests verwendet wird. Diese unterscheiden sich jeweils hinsichtlich ihrer Voraussetzungen, Hypothesen, sowie der Berechnung der Prüfstatistik. Welchen der drei verschiedene Varianten Sie benötigen, hängt von den Daten ab, die Sie vorliegen haben.
t-Test für unabhängige Stichproben
Der in der Praxis am häufigsten angewendete t-Test ist der t-Test für unabhängige Stichproben. In diesem Fall testen wir, ob sich die Mittelwerte zwischen zwei unabhängigen Gruppen signifikant voneinander unterscheiden (Bei mehr als zwei Stichproben kommen andere testverfahren, z.B. die Varianzanalyse zum Einsatz). Die unabhängige Variable ist dementsprechend dichotom (meist Gruppe 1 und Gruppe 2 oder „Männliche Kunden“ und „weibliche Kundinnen“). Mögliche Fragestellungen wären hierbei: „Kaufen Männer mehr Burger als Frauen?“ oder „Schmeckt der vegane Burger FiveProfs-Kunden besser als der Vegetarische?“ (Geschmackmessung mittels einer Likert-Skalierung).
t-Test für abhängige Stichproben
Die zweite Art der t-Testung ist der t-Test für abhängige Stichproben. Auch in diesem Fall möchten wir herausfinden, ob sich zwei Gruppen signifikant voneinander unterscheiden. Jedoch sind die beiden Gruppen in diesem Fall abhängig voneinander oder es handelt sich um verbundene Stichproben. Üblicherweise ist dies dann der Fall, wenn wir eine Messwiederholung haben. Also die selben Personen zu zwei Zeitpunkten befragt werden. Beispielsweise möchten wir testen, ob man nach dem Essen eines Burgers mehr Endorphine im Körper hat als zuvor. Hierbei wird ein und dieselbe Person zu zwei verschiedenen Messzeitpunkten hinsichtlich der Endorphine im Blut untersucht. Da das Endorphinlevel des zweiten Messzeitpunkts unter anderem davon abhängt, wie viele Endorphine vor dem Essen der Burgers im Blut waren, bedingen sich die beiden Werte gegenseitig.
Einstichproben-t-Test
Der letzte Fall, in dem ein t-Test zum Einsatz kommt, ist, wenn wir erfassen möchten, ob sich der Mittelwert eine Stichprobe signifikant von einem bekannten Wert der Population unterscheidet. In solch einem Fall rechnen wir einen Einstichproben-t-Test. Dadurch können wir Fragestellungen beantworten, wie: „Haben Five-Prof Kunden einen höhren IQ als der Durchschnittsbürger (der einen IQ von 100 hat)?“. Im Grunde beantwortet der t-Test für eine Stichprobe die selbe Fragestellung wie der Z-Test, den Sie bereits in Kapitel 11 kennengelernt haben. Der einziger Unterschied zwischen den beiden Tests ist, dass Sie für den Z-Test die Populationsvarianz σ2 kennen müssen. Im Falle des Einstichproben-t-Tests kennen wir diese nicht und schätzen sie deshalb auf Basis der Stichprobenvarianz.
Weitere Beispiele und eine Übersicht, wann Sie welchen Test benutzen sollten, gibt es im folgenden Video.
14.3 T-Test | Einstichproben-, Abhängiger- und Unabhängiger T-Test
15.3 t-Test für unabhängige Stichproben
Beginnen wir mit dem häufigsten t-Test in der Praxis: dem t-Test für zwei unabhängige Stichproben. Dieser Test überprüft, ob sich zwei unabhängige Stichproben hinsichtlich ihres Mittelwerts unterscheiden. Zur Veranschaulichung des Vorgehens bedienen wir uns des Beispiels aus der Einleitung. Stellen Sie sich vor, wir möchten herausfinden, ob es einen Unterschied in der durchschnittlichen Besuchszeit unserer FiveProfs-Filiale gibt, wenn wir „Comfort-Luxe“ Sofas statt unsere normalen Sofas in der Filiale platzieren. Dafür statten wir unsere Filiale in Stuttgart mit den „Comfort-Luxe“-Sofas aus und vergleichen die durchschnittliche Besuchszeit mit unserer Filiale in Nürnberg, die die normalen Sofas besitzt (Hierbei haben wir sichergestellt, das beide Filialen im Hinblick auf die sonstige Ausstattung, die Lage etc. sehr ähnlich sind).
weitere Beispiele für mögliche Fragestellungen:
- Ist eine Therapie erfolgreicher als keine Therapie?
- Ist eine neue Behandlungsmethode besser als die bisherige?
- Verkauft sich ein Produkt besser mit dem Zusatz „NEU“?
- Sind Mitarbeiter in Einzelbüros produktiver als in Großraumbüros?
Hypothesen
Zunächst bilden wir die Hypothesen. Bei ungerichteten Fragestellungen (wie in unserem Beispiel) lauten die allgemeinen Hypothesen des t-Tests für unabhängige Stichproben wie folgt:
H0: Es gibt keinen Unterschied in den Mittelwerten zwischen beiden Testgruppen (μ1 = μ2 bzw. μ1 – μ2 = 0)
H1: Es gibt einen Unterschied in den Mittelwerten zwischen beiden Testgruppen (μ1 ≠ μ2 bzw. μ1 – μ2 ≠ 0)
Haben wir hingegen bereits eine Hypothese über die Richtung des Unterschieds, testen wir gerichtete Hypothesen mit folgendem Hypothesenpaar:
H0: Testgruppe 1 ist schlechter (besser) als oder gleich Testgruppe 2 (μ1 ≤ μ2 bzw. μ1 ≥ μ2)
H1: Testgruppe 1 ist besser (schlechter) als Testgruppe 2 (μ1 > μ2 bzw. μ1 < μ2)
In unserem Beispiel möchten herausfinden ob es einen Unterschied in der durchschnittlichen Besuchszeit unserer FiveProfs-Filiale gibt, wenn wir „Comfort-Luxe“ Sofas statt unsere normalen Sofas in der Filiale platzieren. Wir prüfen damit eine ungerichtete Fragestellung. Unser Hypothesenpaar lautet in diesem Fall:
H0: Es gibt keinen Unterschied in den mittleren Besuchszeiten zwischen beiden Filialen (μComfort = μNormal )
H1: Es gibt einen Unterschied in den mittleren Besuchszeiten zwischen beiden Filialen (μComfort ≠ μNormal )
Noch Fragen offen geblieben? Das folgende Video veranschaulicht Ihnen die möglichen Hypothesen der t-Tests anhand eines DJ-Beispiels in der FiveProfs-Kette.
Voraussetzungen
Nach der Aufstellung der Hypothesen, gilt es die Voraussetzungen zu überprüfen. Der T-Test hat als parametrischer Tests ist „höchsten“ Voraussetzungen, wenn es darum geht Unterschiede zwischen zwei Gruppen zu testen. Dafür besitzt er aber auch die größte Power (=Wahrscheinlichkeit, dass ein Effekt entdeckt wird, wenn ein Effekt auch tatsächlich existiert). Die Voraussetzungen sind:
- Die Messwerte von verschiedenen Personen sind unabhängig voneinander.
Unabhängige Beobachtungen bedeuten, dass die Messwerte eines Probanden nicht von den Messwerten eines anderen Probanden abhängen. Um dies zu gewährleisten, können wir in beiden Stichproben verschiedene Personen befragen, die zufällig ausgewählt werden oder wie in unserem Beispiel verschiedene Personen an zwei unterschiedlichen Orten befragen.
Darüber hinaus gibt es eine Reihe von Voraussetzungen, die in Bezug auf die abhängige Variable (in unserem Beispiel ist das die Besuchszeit), gelten. Die Messwerte der abhängigen Variable müssen:
- mindestens intervallskaliert sein
- möglichst kleine Ausreiser haben
- in beiden Grundgesamtheiten normalverteilt sein
Diese Voraussetzung müssen wir testen, wenn eine oder beide Stichprobengrößen kleiner als 30 sind. In diesen Fällen müssen wir vor dem eigentlichen T-Test einen Test auf die Normalverteilung durchführen. Mögliche Tests wären z.B. der Shapiro-Wilk-Test, Kolmogorow-Smirnow-Test oder Lilliefors-Test. Sie testen inwieweit die vorliegenden Messwerte von der Normalverteilung abweichen. Um die Voraussetzung von normalverteilten Daten zu erfüllen sollten sie deshalb nicht signifikant werden.
Ab einer Größe von n ≥ 30 können wir basierend auf dem zentralen Grenzwerttheorem konventionsgemäß von einer Normalverteilung in der Stichprobenkennwerteverteilung ausgehen (Näheres zum zentralen Grenzwerttheorem finden sie im Kapitel Konfidenzintervalle) und können diese Voraussetzung somit als erfüllt erachten. - in beiden Grundgesamtheiten Homoskedastizität aufweisen.
Homoskedastizität ist gegeben, wenn die Varianzen in beiden Grundgesamtheiten gleich sind. Praktisch bedeutet dies für uns, dass sich die Varianzen der beiden gezogenen Stichproben nicht signifikant unterscheiden dürfen. Man spricht auch von Varianzhomogenität. Um dies zu überprüfen, muss vor jedem T-Test ein Test auf Varianzhomogenität durchgeführt werden. Das gängigste Verfahren ist hierzu der Levene-Test, der im Falle der Varianzhomogenität nicht signifikant wird.
Doch was passiert, wenn eine der Voraussetzungen nicht erfüllt ist? Der T-Test reagiert meist robust auf solche Verletzungen. Ausnahmen sind unterschiedlich große Stichproben und Varianzen. Dann müssen wir auf andere Testverfahren, wie z.B. nicht-parametrische Tests, ausweichen, die geringere Voraussetzungen haben. Die folgende Tabelle zeigt Ihnen welche Tests sich in den jeweiligen Fällen eignen.
| nicht erfüllte Voraussetzung | Alternativtest |
| Intervallskalierung | Man-Whitney-U-Test (ordinal) Wilcoxon-Rangsummen-Test (ordinal) Chi-Quadrat-Test (nominal) |
| Normalverteilung | Man-Whitney-U-Test Wilcoxon-Rangsummen-Test |
| Homoskedastizität | Welch-Test (intervall) Man-Whitney-U-Test (ordinal) Wilcoxon-Rangsummen-Test (ordinal) |
| unabhängige Stichproben | t-Test für abhängige Stichproben |
Falls noch Fragen bezüglich den einzelnen Voraussetzungen offen sind oder sie nochmal genau wissen wollen, was es mit der Homoskedastizität auf sich hat, bietet das folgende Video nochmal eine Wiederholung.
Berechnung der Prüfgröße
Nun kommen wir zur eigentlichen Testung unsrer Hypothese. Hierzu berechnen wir im ersten Schritt die Mittelwerte in beiden Stichproben, die wir im Weiteren auf einen signifikanten Unterschied hin testen. Nehmen wir zur Veranschaulichung noch einmal unser Beispiel mit den Comfort-Sofas: In der Filiale mit den Comfort-Sofas berechnen wir eine durchschnittliche Besuchszeit von 1= 20 min (n=35) und in der Kontroll-Filiale ohne Comfort-Sofas eine Verbleibungsdauer von 2= 14 min (n=35). Nun können wir über die Prüfgröße T die Wahrscheinlichkeit für die gefundene Differenz von 6 Minuten bestimmen unter Annahme, dass beide Stichproben aus der selben Population stammen. Ihre Formel lautet wie folgt:

Um herauszufinden, ob der Unterschied groß genug ist, sodass wir nicht mehr von einem Zufallsprodukt ausgehen können, setzt der T-Wert die Differenz der Mittelwerte in Relation zur Streuung. Konkret wird hierbei der Standardfehler des Schätzers der Differenz der Mittelwerte als Maßstab verwendet, um die Größe der Differenzen einzuschätzen.
Doch wie berechnen wir den Standardfehler des Schätzers der Differenz der Mittelwerte? Wir können ihn aus der Populationsvarianz bzw. durch dir korrigierte Stichprobenvarianz (wenn wir die Populationsvarianz nicht kennen sollten) schätzen.

Hierbei sollte beachtet werden, dass die Formeln lediglich für balancierte Designs gelten – sprich wenn beide Stichproben gleich groß sind. Wenn verschiedene Stichprobengrößen vorhanden sind, wird eine korrigierte Formel zur Berechnung des Standardfehlers verwendet.
Schätzung der Populationsvarianz durch die Stichprobe
Falls wir den Schätzer der Populationsvarianz nicht kennen sollten (was in der Forschung normalerweise der Fall ist), können wir ihn aus der Stichprobe selbst schätzen. Die Formel lautet wie folgt:
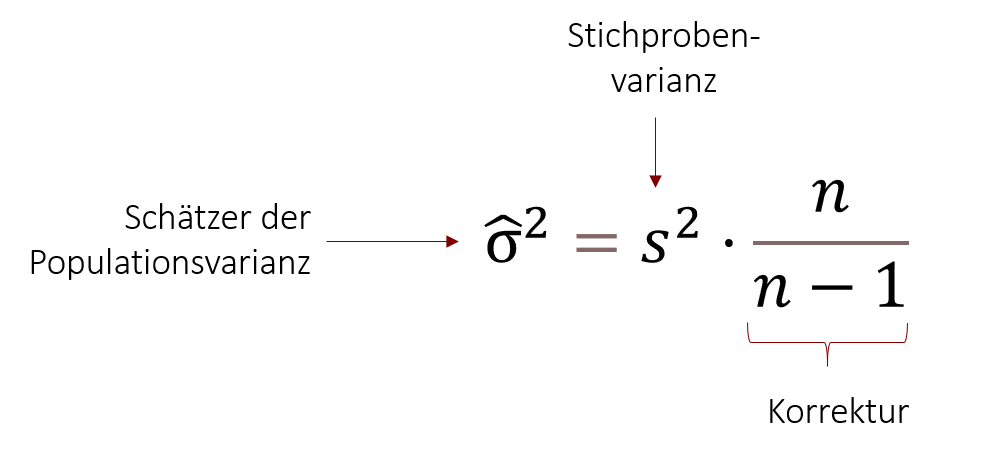
In diese Formel können wir nun unsere erhobenen Kennwerte aus den Stichproben einsetzen und so den empirischen T-Wert ermitteln, den wir anschließend gegen den kritischen T-Wert testen und so unsere Hypothese entweder bestätigen oder ablehnen.
Beispiel: Comfort-Luxe Sofas in den FiveProfs Filialen
Wir möchten die Hypothese überprüfen, ob es einen Unterschied in der Besuchsdauer gibt, wenn wir Comfort-Luxe Sofas in unseren Five-Profs Filialen platzieren. Dazu haben wir in zwei Filialen unabhängige Stichproben von jeweils n=35 Kunden gezogen. Die durchschnittliche Besuchszeit in der Filiale mit den Comfort-Sofas war 1= 20 Minuten (Standardabweichung = 6,5 Minuten) und in der Kontroll-Filiale ohne Comfort-Sofas 2= 14 Minuten (Standardabweichung = 6 Minuten). Berechnen Sie die Prüfgröße T:
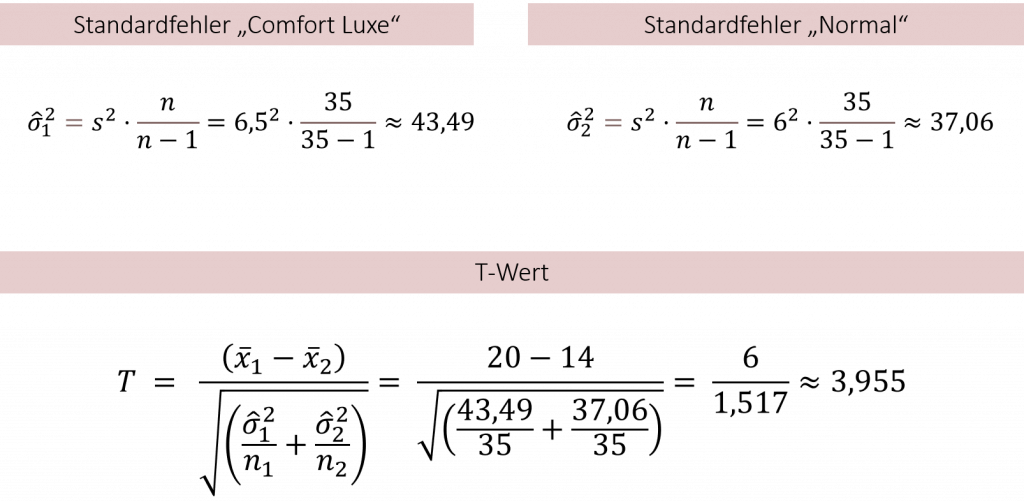
Als weiteres Beispiel zeigt Ihnen das folgende Video ein weiteres Rechenbeispiel zum T-Test.
14.5 T-Test | Rechenbeispiel Unabhängiger T-Test
Interpretation des t-Werts
Im nächsten Schritt ermitteln wir, wie wahrscheinlich das Auftreten unseres empirisch errechneten t-Werts unter der Annahme der Nullhypothese (H0: Es gibt keinen Unterschied zwischen den beiden Gruppen) ist. Ist das Auftreten „unwahrscheinlich genug“ können wir die Nullhypothese ablehnen und unsere Alternativhypothese bestätigen. Was hierbei als „unwahrscheinlich genug“ gilt, legen wir im Vorhinein mit unserem Signifikanzniveau fest. Die nachfolgende Tabelle zeigt Ihnen nochmal die gängigen Signifikanzniveaus.
Schritt 1: kritischen t-Wert ermitteln
Abhängig von diesem Signifikanzniveau und je nach Art der Hypothese (einseitig oder zweiseitig) können wir nun einen kritischen t-Wert (tkrit) definieren. Dieser bildet den Grenzwert, bei dessen Überschreitung (bzw. Unterschreitung) wir unsere Nullhypothese ablehnen können. Die nachfolgende Tabelle zeigt Ihnen, welcher kritischer t-Wert bei welcher Hypothese eingesetzt wird. α steht hierbei für das verwendete Signifikanzniveau und df für den Freiheitsgrad. Bei balancierten Designs (=Stichproben sind gleich groß) lautet die Formel für die Berechnung des Freiheitsgrads wie folgt: df = n1 + n2 – 2
|
ungerichtet |
gerichtet |
gerichtet |
|
| Hypothese |
H0: μ1 = μ2 H1: μ1 ≠ μ2 |
H0: μ1 ≤ μ2 H1: μ1 > μ2 |
H0: μ1 ≥ μ2 H1: μ1 < μ2 |
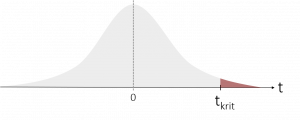
| kritischer T-Wert | tkrit = ± t1-α/2, (df) | tkrit = t1-α, (df) | tkrit = tα, (df) |
 |
 |
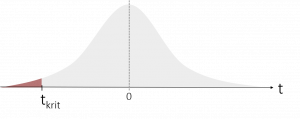 |
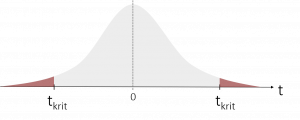
Über die Tabellen der t-Verteilung können wir daraufhin den entsprechenden kritischen t-Wert heraussuchen. Hierzu suchen wir zunächst in der ersten Spalte den entsprechenden Freiheitsgrad, den wir zuvor berechnet haben, heraus. Abhängig vom gewählten Signifikanzniveau suchen wir uns anschließend den t-Wert aus, der die entsprechende Fläche abbildet. Als Beispiel: Bei einem gewählten Signifikanzniveau von α = 5% und einer ungerichteten (beidseitigen) Hypothese, nehmen wir den t-Wert für die Fläche von 0,975 (da sich die 5% auf beide Seiten aufteilen). Bei einem Freiheitsgrad von df = 10 (nur als Beispiel) erhalten wir so einen kritischen t-Wert von tkrit = ± t1-0,05/2, (10) = ±2,228.
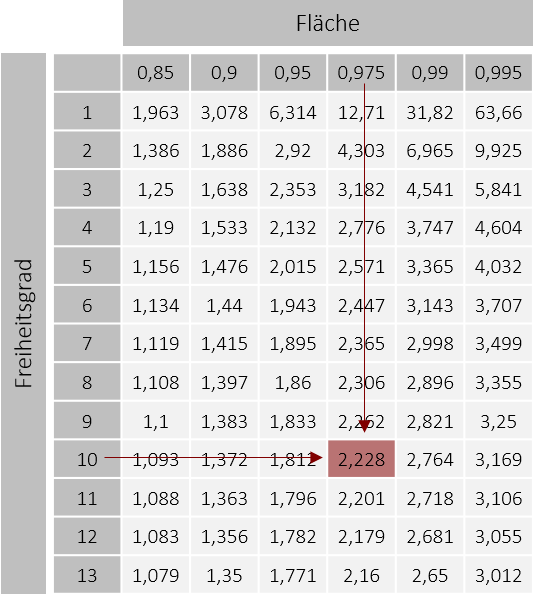
Wenn der Freiheitsgrad größer als 30 ist, nähert sich die t-Verteilung so stark an die Standardnormalverteilung an, sodass wir in diesen Fällen einen z-Wert als Näherungswert für den t-Wert benutzen können. In diesen Fällen suchen wir in der Tabelle der z-Verteilung den z-Wert, der die selbe Fläche abdeckt, wie unser gesuchter t-Wert. Das nachfolgende Beispiel zeigt Ihnen eine mögliche Situation:
Beispiel
In unserem Beispiel prüfen wir, ob es einen Unterschied in der Besuchszeit zwischen FiveProfs Filialen mit Comfort-Luxe Sofas und ohne gibt. Dafür haben wir zu Beginn folgende Hypothesen aufgestellt:
H0: Es gibt keinen Unterschied in der mittleren Besuchszeit zwischen beiden Filialen (μComfort = μNormal )
H1: Es gibt einen Unterschied in den mittleren Besuchszeiten zwischen beiden Filialen (μComfort ≠ μNormal )
Unsere ermittelte Prüfgröße T = 3,955 (temp). Nun möchten wir entscheiden, ob wir mit einer Irrtumswahrscheinlichkeit von 5% die H0 ablehnen können, oder nicht. Die Stichprobengrößen betragen jeweils 35 Personen. Die Hypothese ist ungerichtet.
- Freiheitsgrad berechnen
df = n1 + n2 – 2 = 35 + 35 – 2 = 68 - kritischen T-Wert berechnen
da df > 30 kann in die Standardnormalverteilung approximiert werden. Wir können dementsprechend einen z-Wert als Näherungswert annehmen.
tkrit = ± t1-0,05/2, (68) ≈ ± z1-0,05/2 = ± z0,975 = ± 1,96
Schritt 2: Entscheidung
Wurde der kritische und empirische T-Wert ermittelt, kann daraufhin die Entscheidung getroffen werden, ob wir die Nullhypothese verwerfen oder beibehalten. Abhängig von der Hypothese (einseitig oder zweiseitig) lehnen wir die Nullhypothese ab, wenn der kritische t-Wert durch unsere Prüfgröße über- bzw. unterschritten wird und somit temp im Ablehnungsbereich liegt.
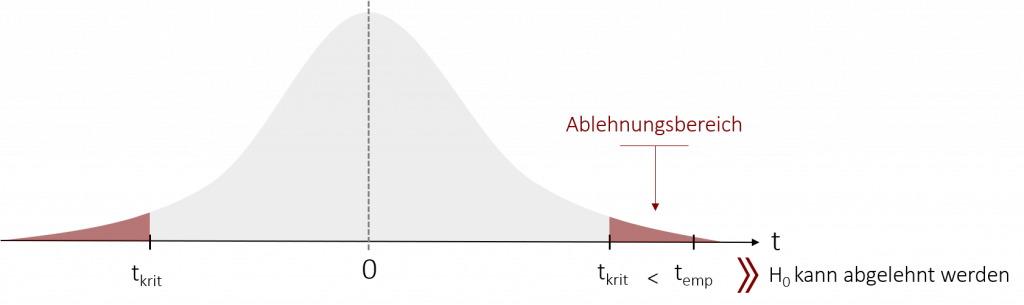
Um dies herauszufinden, stellen wir die Prüfgröße (temp) und den kritischen t-Wert (tkrit) gegenüber und vergleichen die beiden. Die folgende Tabelle zeigt Ihnen auf, in welchen Fällen wir die Nullhypothese ablehnen können.
| Hypothese | H0: μ1 = μ2
H1: μ1 ≠ μ2 |
H0: μ1 ≤ μ2
H1: μ1 > μ2 |
H0: μ1 ≥ μ2
H1: μ1 < μ2 |
| empirischer T-Wert (temp) | 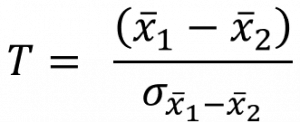 |
||
| kritischer T-Wert (tkrit) | tkrit = ± t1-α/2, (df) | tkrit = t1-α, (df) | tkrit = tα, (df) = -t1-α, (df) |
| H0 ablehnen, wenn | |temp | > tkrit | temp > tkrit | temp < tkrit |
Beispiel: Comfort-Luxe Sofas in den FiveProfs Filialen
In unserem Beispiel prüfen wir, ob es einen Unterschied in der Besuchszeit zwischen FiveProfs Filialen mit Comfort-Luxe Sofas und ohne gibt. Dafür haben wir zu Beginn folgende Hypothesen aufgestellt:
H0: Es gibt keinen Unterschied in der mittleren Besuchszeit zwischen beiden Filialen (μComfort = μNormal )
H1: Es gibt einen Unterschied in den mittleren Besuchszeiten zwischen beiden Filialen (μComfort ≠ μNormal )
Unsere ermittelte Prüfgröße ist T = 3,955 (temp). Unser kritischer t-Wert lautet tkrit= ± 1,96. Nun möchten wir entscheiden, ob wir mit einer Irrtumswahrscheinlichkeit von 5% die H0 ablehnen können, oder nicht. Die Stichprobengrößen betragen jeweils 35 Personen.
Entscheidung
|temp | > tkrit
|3,995| > ±1,96 -> H0 ablehnen.
Antwort: Es gibt einen hoch signifikanten Unterschied in der Besuchszeit zwischen FiveProfs Filialen mit Comfort-Luxe Sofas und ohne (Irrtumswahrscheinlichkeit 5%).
Falls noch Fragen offen geblieben sind oder Sie näher verstehen möchten, was es mit den Flächen in den Tabellen auf sich hat, gibt Ihnen das folgende Video einen guten Überblick. Zudem wird die Konstruktion des Ablehnungsbereichs im Kapitel z-Tests ausführlicher erklärt.
15.4 t-Test für abhängige Stichproben
Der t-Test für abhängige Stichproben prüft (ebenso wie der t-Test für unabhängige Stichproben), ob es einen signifikanten Unterschied zwischen zwei Mittelwerten gibt. Er beantwortet dabei Fragestellungen wie: „Sind FiveProfs Kunden nach dem Verzehr unserer Burger glücklicher?“ oder „Ist man am Ende einer Warteschlange frustrierter als in der Mitte der Warteschlange?“. Diese Fragen könnte man ebenso gut mit einem t-Test für unabhängige Stichproben beantworten. Das entscheidende Kriterium, weshalb wir uns dennoch für einen t-Test für abhängige Stichproben entscheiden, liegt im Versuchsdesign. In Fall des t-Tests für abhängige Stichproben gehen wir davon aus, dass sich die beiden Mittelwerte gegenseitig beeinflussen. Beispielsweise dadurch, dass wir ein und dieselbe Person zwei Mal befragen – sprich: wenn wir ein Messwiederholungsdesign haben. Solch ein Design lohnt sich, da die Fehlervarianz wegfällt, die wir normalerweise hätten, wenn wir unterschiedliche Personen befragen würden.
weitere Beispiel-Fragestellungen
- Wird ein Produkt nach Betrachten einer Werbung besser bewertet als vorher?
- Steigt die Arbeitszufriedenheit nach Durchführung von Trainings?
- Werden zwei Produktvarianten unterschiedlich von einer Stichprobe bewertet?
Hypothesen
Bevor wir uns den Hypothesen widmen, sollten wir uns zunächst die „Testlogik“ vergegenwärtigen. Denn der t-Test für abhängige Stichproben stellt nicht wie der t-Test für unabhängige Stichproben beide Mittelwerte gegenüber, um zu überprüfen, ob sie sich unterscheiden, sondern bedient sich eines Zwischenschritts. Er bildet zunächst die Differenz aus den beiden Mittelwerten (μd= μ1 – μ2) und überprüft daraufhin, ob sich diese Differenz signifikant von Null unterscheidet. Statt also zu überprüfen, ob beide Mittelwerte gleich sind, prüft er, ob die Differenz der beiden Mittelwerte gleich Null ist. Dementsprechend unterscheiden sich auch die Hypothesen und lauten um ungerichteten Fall:
H0: Der Mittelwert der Differenzen ist gleich Null. (μd = 0) (=Es gibt keinen Unterschied zwischen den Mittelwerten beider Stichproben)
H1: Der Mittelwert der Differenzen ist ungleich Null. (μd ≠ 0) (=Es gibt einen Unterschied zwischen den Mittelwerten beider Stichproben)
Ebenso ändern sich auch die Hypothesen für gerichtete Fragestellungen:
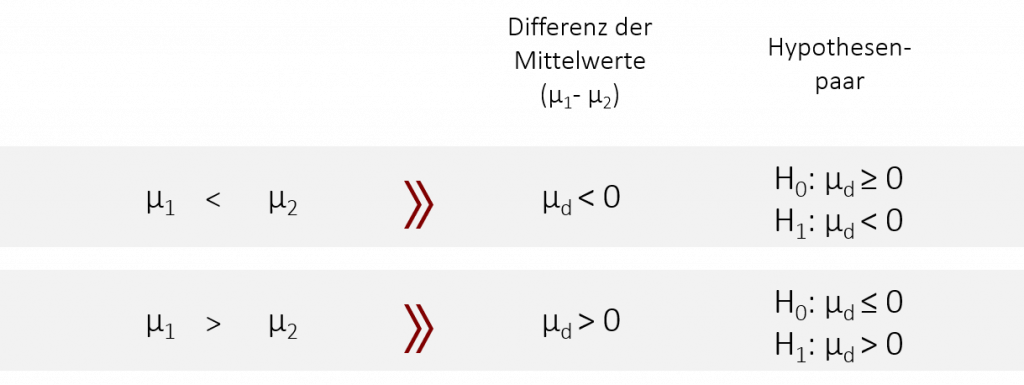
Beispiel
Wir möchten herausfinden, ob FiveProfs Kunden nach dem Verzehr eines Burgers glücklicher sind als zuvor. Dafür überprüfen wir einmal vor und einmal nach dem Verzehr den Serotonin-Spiegel der Kunden. Wenn unsere Hypothese stimmt, sollten die Kunden nach dem Verzehr (μnachher) einen höheren Serotonin-Wert aufweisen als zuvor (μvorher).
μvorher < μnachher
dementsprechend ist: μd < 0
Unsere Hypothesen lauten somit:
H0: Der Serotonin-Wert nach dem Burger ist kleiner oder gleich dem Serotonin-Wert vor dem Verzehr des Burgers (=Die Differenz der Mittelwerte ist größer oder gleich Null)
H1: Der Serotonin-Wert ist nach dem Verzehr des Burgers größer als vorher. (=Die Differenz der Mittelwerte ist kleiner als Null)
oder statistisch ausgedrückt:
H0: μd ≥ 0
H1: μd < 0
Voraussetzungen
Bevor wir mit der Testung der Hypothese beginnen, müssen wir zuvor die Voraussetzungen überprüfen. Die erste ist, wie der Name schon vermuten lässt:
- die Stichproben müssen abhängig voneinander sein.
Dies kommt entweder durch eine Messwiederholung (=zwei Messungen an derselben Person) oder zwei parallelisierten Gruppen zustande.
Die restlichen Voraussetzungen beziehen sich auf die abhängige Variable (in unserem Beispiel der Serotonin-Spiegel). Wichtig hierbei ist, dass die Voraussetzungen sich nicht auf die gemessenen Serotonin-Werte aus den einzelnen Stichproben beziehen, sondern auf die Differenzen der Messpaare. Stellen sie sich vor, sie erstellen eine neue Variable in Ihrem Datensatz, die μ1 – μ2 subtrahiert. Sie erhalten eine neue Spalte, die die Differenzen zwischen den beiden Messzeitpunkten abbildet. Eben diese Messwerte müssen:
- intervallskaliert sein
Wird die Voraussetzung nicht erfüllt, müssen wir auf ein verteilungsfreies Testverfahren zurückgreifen. Der Vorzeichentest bietet solch eine Alternative. - normalverteilt sein
Diese Voraussetzung müssen wir bei n < 30 testen. In diesen Fällen führen wir vor dem eigentlichen t-Test einen Test auf die Normalverteilung durchführen. Mögliche Tests wären z.B. der Shapiro-Wilk-Test, Kolmogorow-Smirnow-Test oder Lilliefors-Test. - Die Messwerte der beiden Zeitpunkte sollten positiv miteinander korrelieren, da ansonsten der Test einiges an Teststärke (Power) einbüßt
Der t-Test reagiert relativ robust auf Verletzungen der Voraussetzungen. Dennoch sollten Sie auf alternative nicht-parametrische Verfahren umsteigen, wenn einige Voraussetzungen verletzt werden. Die folgende Tabelle zeigt Ihnen, welche Verfahren sich bei welcher Verletzung eignen:
| nicht erfüllte Voraussetzung | Alternativtest |
| abhängige Gruppen | t-Test für unabhängige Stichproben |
| Intervallskalierung | Vorzeichentest (ordinal) Bowker Test (nominal) McNemar Test (dichotom) |
| Normalverteilung | Vorzeichenrangtest (Wilcoxon) |
| positive Korrelation zwischen Messwerten | Vorzeichenrangtest (Wilcoxon) |
Falls noch Fragen offen sind, bietet das folgende Video einen weiteren Überblick.
Berechnung der Prüfgröße
Um die Wahrscheinlichkeit für die gefundene Differenz zu berechnen, ermitteln wir wieder die Prüfgröße t. Sie berechnet sich in diesem Fall jedoch über den Mittelwert der Differenzen der Messpaare, weshalb die Formel leicht von der der t-Tests für unabhängige Stichproben abweicht.

Da die Berechnung bei größeren Gruppen sehr aufwändig ist, lohnt es sich die Prüfgröße t durch SPSS oder andere Statistikprogramme ermitteln zu lassen. Wenn Sie kleine Stichproben haben, hilft bei der Berechnung der Prüfgröße eine Hilfstabelle, wie das folgende Beispiel zeigt:
Händische Berechnung der Prüfgröße t
Wir möchten die These überprüfen, ob FiveProfs Kunden nach unseren Burgern glücklicher sind als zuvor und messen hierzu den Serotonin-Spiegel vor und nach dem Verzehr eines Burgers. Die Werte stehen in der unterstehenden Tabelle:
| Serotonin vorher (ng /ml) | Serotonin nachher (ng/ml) |
| 120 | 126 |
| 168 | 182 |
| 150 | 152 |
| 197 | 208 |
| 123 | 130 |
Zunächst machen wir eine Hilfstabelle, die die Differenzen abbildet:
| Serotonin vorher (ng /ml) | Serotonin nachher (ng/ml) | Differenz des Serotonin-Spiegels (ng/ml) |
| 120 | 126 | -6 |
| 168 | 182 | -14 |
| 150 | 152 | -2 |
| 197 | 208 | -11 |
| 123 | 130 | -7 |
Diese Differenzen der Mittelwerte können wir nun in die Formel einsetzen, um die empirische Prüfgröße zu berechnen:
- Mittelwert der Differenzen der Messwertpaare berechnen
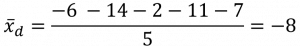
- Standardfehler der Messwertunterschiede berechnen
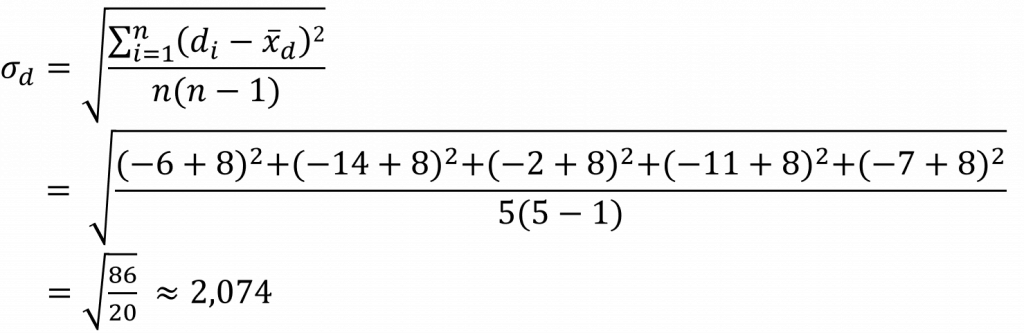
- Prüfgröße t berechnen
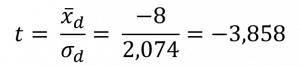
Interpretation des t-Werts
Um unsere im Vorhinein aufgestellte Hypothese entweder anzunehmen oder verwerfen zu können, stellen wir die Prüfgröße dem kritischen t-Wert gegenüber. Näheres hierzu finden Sie beim t-Test für unabhängig Stichproben, der diese Schritte einzeln darstellt.
Die folgende Tabelle zeigt Ihnen eine Übersicht, in welchen Fällen wir die Nullhypothese ablehnen können. (df =n-1)
| Hypothese | H0: μd = 0
H1: μd ≠ 0 |
H0: μd ≥ 0
H1: μd < 0 |
H0: μd ≤ 0
H1: μd > 0 |
| empirischer T-Wert (temp) | 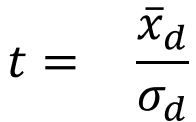 |
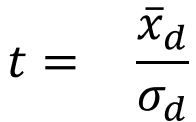 |
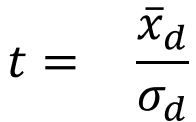 |
| kritischer T-Wert (tkrit) | tkrit = ± t1-α/2, (df ) | tkrit = tα, (df) = -t1-α, (df) | tkrit = t1-α, (df) |
| H0 ablehnen, wenn | |temp | > tkrit | temp < tkrit | temp > tkrit |
Beispiel
Unsere zu überprüfende Fragestellung war, ob FiveProfs Kunden nach dem Konsum eines Burgers glücklicher sind als zuvor (Signifikanzniveau α = 0,05). Daraus ergibt sich folgendes gerichtetes Hypothesenpaar:
H0: Der Serotonin-Wert nach dem Burger ist kleiner oder gleich dem Serotonin-Wert vor dem Verzehr des Burgers (=Die Differenz der Mittelwerte ist größer oder gleich Null)
H1: Der Serotonin-Wert ist nach dem Verzehr des Burgers größer als vorher. (=Die Differenz der Mittelwerte ist kleiner als Null)
H0: μd ≥ 0
H1: μd < 0
- Kritischen t-Wert berechnen
tkrit = tα, (df) = -t1-α, (df) = -t0,95, (4) = -2,1318 - Entscheidung
temp = -3,858 < tkrit = -2,132 –> H0 ablehnen
FiveProfs-Kunden haben nach dem Verzehr eines Burgers einen signifikant höheren Serotoninspiegel und sind dementsprechend glücklicher als vorher (5% Irrtumswahrscheinlichkeit).
15.5 Übungsfragen
Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!
In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!
- Student: The Probable Error of a Mean. In: Biometrika. 6, Nr. 1, 1908, S. 1–25. JSTOR 2331554. doi:10.1093/biomet/6.1.1. ↵

 1= 20 min und in der Kontroll-Filiale
1= 20 min und in der Kontroll-Filiale 
