Varianz- und Regressionsanalyse
18 Multiple Regression
18.0 Einführung Multiple Regression
In Kapitel 5 haben Sie bereits die bivariate Regression kennengelernt. Diese basiert auf einem linearen Zusammenhang zwischen einem Prädiktor (unabhängige Variable) und einer abhängigen Variable. Beispielsweise können wir durch eine bivariate Regression die Produktbewertung für einen Burger durch die Geschmacksbewertung (Prädiktor) vorhersagen. Wie gut unser aufgestelltes Modell ist, sagt uns der Determinationskoeffizient R2, welcher beschreibt, wie viel Varianz der abhängigen Variable durch den Prädiktor aufgeklärt werden kann.
Nun ist es in in der Praxis so, dass nicht nur ein Faktor, sondern mehrere unabhängige Faktoren eine abhängige Variable beeinflussen können und somit auch für ihre Vorhersage in Betracht kommen. So kann die Produktbewertung unseres Burgers nicht nur durch Geschmacks beeinflusst werden, sondern auch durch den Preis oder das äußere Erscheinungsbild. Um diesen vermuteten Zusammenhang zu testen, berechnen wir eine multiple Regression. Diese modelliert einen linearen Zusammenhang (=eine Regressionsgerade) zwischen einer Kriteriumsvariablen und mehreren Prädiktoren. Dadurch können wir die abhängige Variable nicht nur auf Basis eines Prädiktors, sondern mehrerer Prädiktoren vorhersagen.
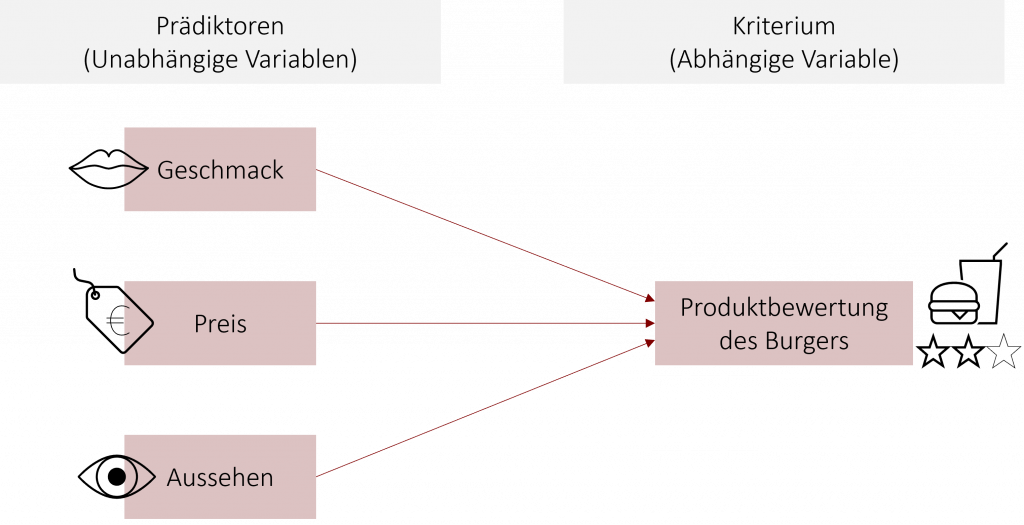
Ziel der multiplen Regression ist es durch die Aufstellung einer Regressionsgeraden möglichst viel Varianz der abhängigen Variable durch die Prädiktoren aufklären zu können. Stellt man sich das bildlich vor, so dient jeder Prädiktor (z.B. Preis, Geschmack) dazu ein Stückchen mehr der Varianz in der Produktbewertung des Burgers aufzuklären (dunkelroter Bereich).
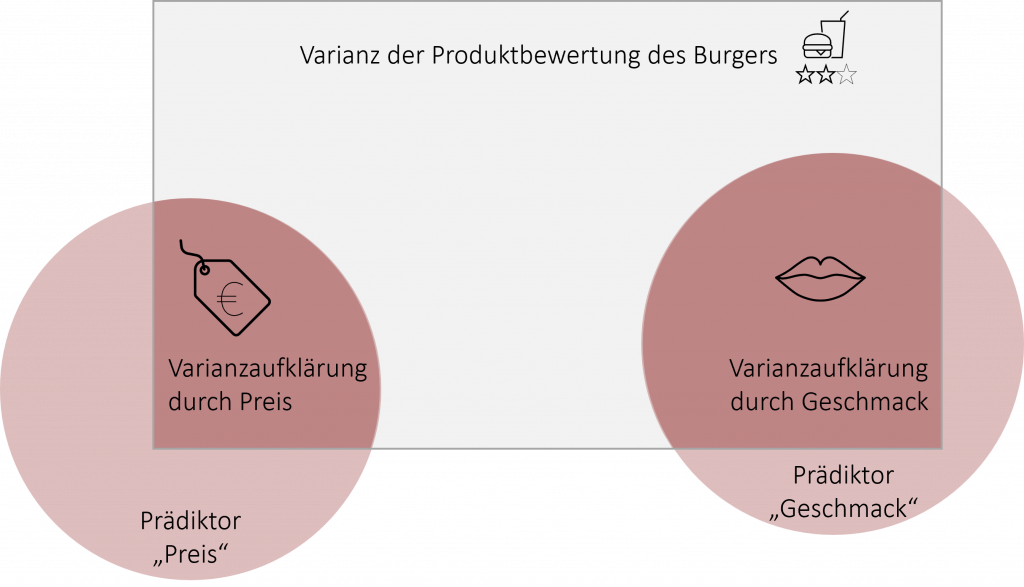
Oft ist es so, dass die Prädiktoren nicht vollständig unabhängig voneinander sind, sondern sich gegenseitig beeinflussen. So auch in unserem Beispiel: Das Auge ist bekanntlich mit und so korrelieren auch unsere beiden Prädiktoren „Aussehen“ und „Geschmack“ miteinander. Dies ist nicht weiter schlimm, solange sich die Korrelationen zwischen den Prädiktoren in Grenzen halten. Jedoch bedeutet dies auch, dass beide Prädiktoren eine gemeinsame Varianzaufklärung besitzen, die sich nicht mehr klar einem Prädiktor zuordnen lässt. Bildlich gesehen überlappen sich die dunkelroten Flächen der beiden korrelierenden Prädiktoren.
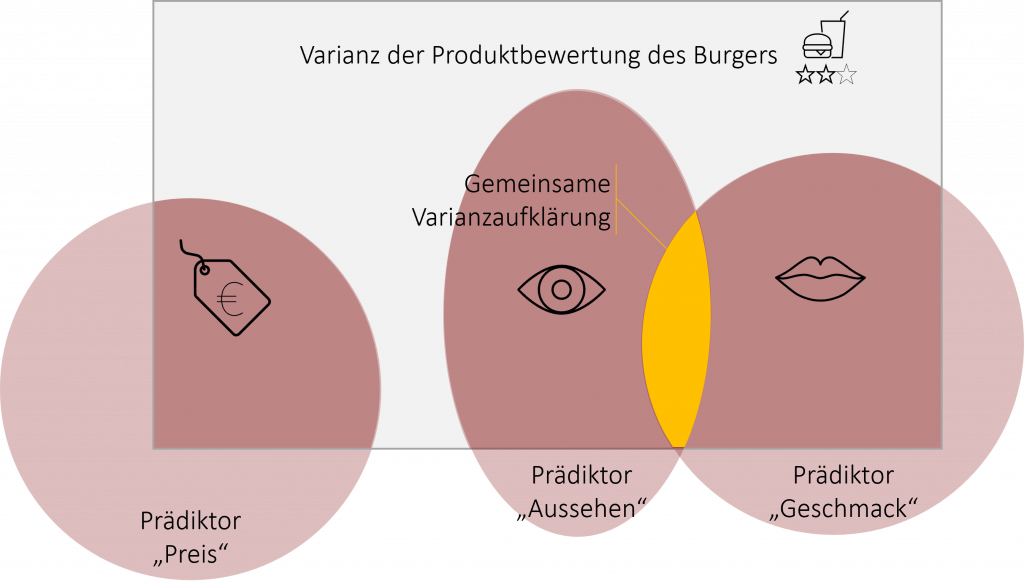
Das besondere bei der multiplen Regression ist nun, das wenn Prädiktoren untereinander korrelieren, nur die neu hinzukommende aufgeklärte Varianz durch den Prädiktor berücksichtigt wird. So wird lediglich die Varianzaufklärung des dunkelroten Bereichs beim Prädiktor „Aussehen“ berücksichtigt.
17.1 Multiple Regression | Einführung
18.1 Regressionsgleichung
Durch die multiple Regression können wir eine Regressionsgleichung aufstellen, die auf Basis der unabhängigen Prädiktoren die abhängige Variable schätzt. Diese Gleichung basiert auf der selben Struktur wie die bivariate Regression (Kapitel 5).
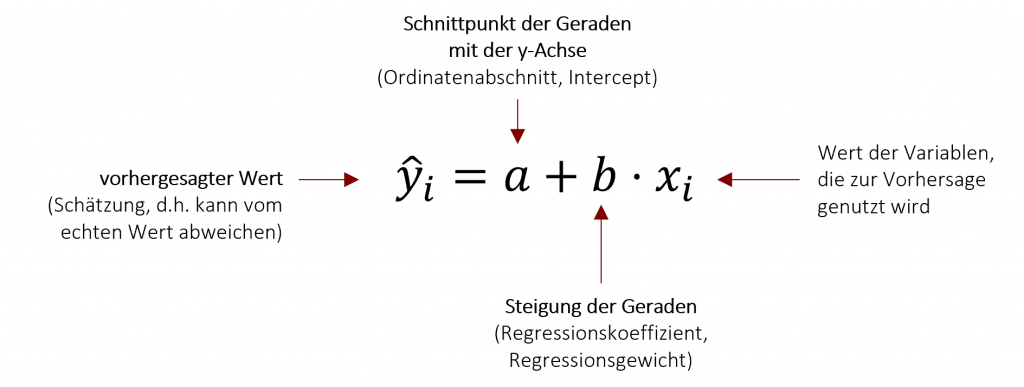
Da bei der multiplen Regression mehr als nur ein Prädiktor betrachtet wird, muss die obenstehende Formel um die weiter hinzukommenden Prädiktoren ergänzt werden. Diese werden in der Regressionsgleichung hintereinander aufaddiert und bilden so die gemeinsame Schätzung für die abhängige Variable.
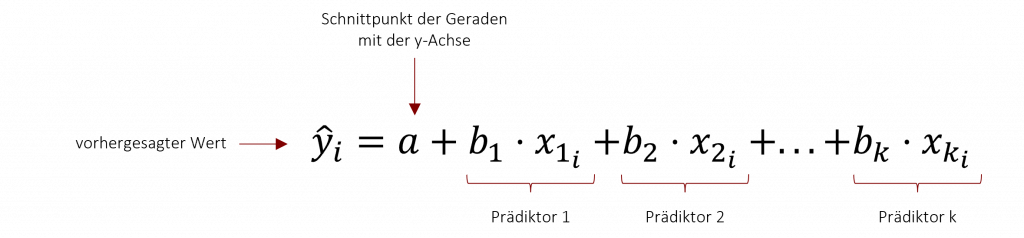
Für unser oben gennanntes Beispiel ergibt sich somit folgende Regressionsgleichung:
![]()
Im Unterschied zur bivariaten Regressionsgleichung gibt es bei der multiplen Regression für jeden einzelnen Prädiktor zwei mögliche Regressionsgewichte – das unstandardisierte Regressionsgewicht b und das standardisierte Regressionsgewicht β (beta). Das unstandardisierte Regressionsgewicht b kennen Sie bereits aus Kapitel 5. Es beschreibt die Steigung der Geraden und ist inhaltlich interpretierbar. Beispielsweise hat unser Prädiktor „Preis“ ein b=-1,5. In diesem Fall sinkt die Produktbewertung unseres Burgers (AV) um 1,5 Bewertungspunkte mit jedem Euro, welcher beim Preis des Burgers hinzukommt. Das unstandardisierte Regressionsgewicht b hat jedoch einen zentralen Nachteil: Wenn die Prädiktoren auf unterschiedlichen Skalen erfasst werden (bspw. ein Prädiktor in € und ein anderer Prädiktor auf einer Likert-Skala), können wir die Regressionsgewichte mehr nicht miteinander vergleichen. Wir wissen nicht, welcher der Prädiktoren nun den größten Einfluss auf die abhängige Variable hat. Um dieses Problem zu lösen, müssen wir unsere Regressionsgewichte an der Standardabweichung standardisieren. So sind sie zwar inhaltlich nicht mehr interpretierbar, jedoch besitzen sie nun ein fest definierten Wertebereich, welcher sich von -1 bis +1 erstreckt. Dadurch lassen sich die β-Gewichte über alle Prädiktoren hinweg vergleichen und wir können zum Beispiel sehr einfach ablesen, welcher Prädiktor den größten Einfluss hat.
| Wertebereich | Eigenschaften | |
| unstandardisiertes Regressionsgewicht b | abhängig von gewählter Skala |
|
| standardisiertes Regressionsgewicht β | [-1, +1] |
|
Noch nicht ganz verstanden? Das nachfolgende Video erklärt Ihnen die Regressionsgleichung der multiplen Regression anhand eines weiteren Beispiels aus der FiveProfs Kette.
17.2 Multiple Regression | Regressionsgleichung
18.2 Voraussetzungen
Vor der Durchführung einer multiplen Regression müssen zunächst die Voraussetzungen geprüft werden. Diese entsprechen zunächst den Voraussetzungen der bivariaten Regression in Kapitel 5:
- metrisch skalierte abhängige und unabhängige Variablen
Bei den Prädiktoren können zudem nominal Skalierte Variablen mithilfe einer Dummy-Codierung in das Regressionsmodell mit aufgenommen werden. - linearer Zusammenhang zwischen den Prädiktoren und der abhängigen Variable
Diese Voraussetzung lässt sich beispielsweise anhand eines Streudiagramms graphisch überprüfen. Sind exponentielle oder logistische Verläufe in den Daten erkennbar, so lohnt es sich auf andere multiple Regressionen, wie beispielsweise die polynomiale oder logistische Regression zurückzugreifen. - Normalverteilung der Residuen
Bei einer ausreichend großen Stichprobengröße kann die Überprüfung dieser Voraussetzung vernachlässigt werden. Laut dem zentralen Grenzwerttheorem kann hierbei eine Normalverteilung unterstellt werden. Bei kleinen Stichproben hingegen sollte zur Bestimmung der Normalverteilung ein entsprechender Test (z.B. Kolmogorov-Smirnov-Test, Lilliefors-Test) oder eine graphische Überprüfung am QQ-Plot durchgeführt werden. - Homoskedastizität (=Varianzhomogenität)
Diese kann über den Levene Test oder graphisch überprüft werden. Für die graphische Überprüfung eignet sich im Statistikprogramm R das Scale-Location-Diagramm. Um Homoskedastizität unterstellen zu können, sollten die Datenpunkte im Diagramm gleichmäßig streuen und die darin enthaltene Linie sollte ungefähr parallel zur x-Achse verlaufen. - Ausreiser oder einflussreiche Punkte
Diese können mit Hilfe einer Leverage-Analyse erkannt und bei Bedarf eliminiert werden. Bei der Leverage-Analyse wird der Hebel ( engl. Leverage) bzw. der Einfluss eines Wertes auf die Regressionsgerade bestimmt. Ein großer Hebel bei einem Datenpunkt ist soweit unbedenklich, wenn sich der Wert „konform“ zur Regressionsgeraden verhält. Trotz hoher Hebelwirkung ändert er in diesem Fall den Verlauf der Regressionsgleichung kaum. Kritisch wird es, wenn ein Wert einen hohen Einfluss auf die Regressionsgerade hat und gleichzeitig eine hohe Abweichung von der Vorhersage aufweist. Dann beeinflusst er den Verlauf der gesamten Regressionsgleichung in hohem Maße und kann zu Verzerrungen in der Vorhersage führen. Das Maß für solch einen einflussreichen Punkt ist die Cook’s Distance. Ist diese größer als 0,5, wird der Wert als Ausreiser bewertet. Diese Cook’s Distance kann beispielsweise im Residuals vs. Leverage Diagramm im Statistikprogramm R graphisch bestimmt werden. Liegen die Werte hinter der gestichelten Linie, handelt es sich um einen Ausreiser
Zu diesen Voraussetzungen, die Sie bereits aus der bivariaten Regression kennen, kommen noch zwei weitere hinzu:
- Unabhängigkeit der Residuen (=Keine Autokorrelation der Residuen)
Diese Voraussetzung ist verletzt, wenn die Ausprägung eines Residuums zu einem bestimmten Messzeitpunkt von einem zeitlich früherem Residuum beeinflusst wird. Residuen können untereinander korrelieren, wenn z.B. die Fragen in einer Umfrage nicht unabhängig voneinander sind und somit auch ihre Antworten miteinander zusammenhängen. Zur Überprüfung dieser Voraussetzung kann der Durbin-Watson-Test durchgeführt werden. Dieser sollte nicht signifikant werden, um eine Unabhängigkeit in den Residuen unterstellen zu können. - Multikollinearität
Wie schon in der Einleitung beschrieben, können die Prädiktoren untereinander korrelieren. Dies ist nicht weiter problematisch, solange die Korrelationen zwischen den Prädiktoren einen Schwellenwert von r = 0.8 nicht überschreiten. Hierzu können bivariate Korrelationen berechnet werden, oder ersatzweise auch der Variance Inflation Factor (VIF) berechnet werden. Dieser sollte einen Wert kleiner als 10 aufweisen.
Das folgende Video erklärt Ihnen die Voraussetzungen und ihre Überprüfung anhand eines Beispiels aus der FiveProfs Kette.
17.3 Multiple Regression | Voraussetzungen
18.3 Ergebnisse der multiplen Regression
Sind die Voraussetzungen erfüllt, können wir mithilfe von Statistikprogrammen wie SPSS oder R eine multiple Regression berechnen und herausfinden, welche Faktoren einen signifikanten Einfluss auf die Produktbewertung unseres Burgers haben. Als Ergebnis der Berechnung erhalten wir solche (oder ähnliche) Tabelle:
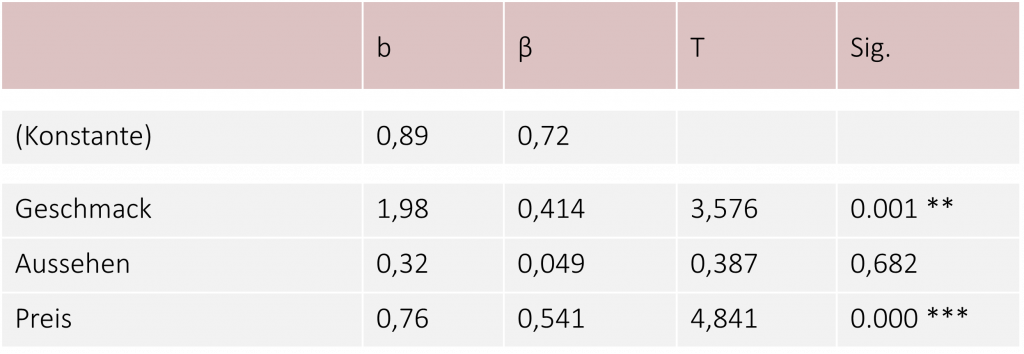
In der ersten Spalte sehen wir die unstandardisierten Regressionsgewichte. Mit ihrer Hilfe können wir unsere Regressionsgleichung aufstellen. Die Konstante (erste Zeile) spiegelt dabei den Ordinatenabschnitt wider. Für unser Beispiel ergibt sich somit folgende Regressionsgleichung:
![]()
In der zweiten Spalte sehen Sie nun die standardisierten Regressionsgewichte β. Diese geben uns Aufschluss über den Einfluss des jeweiligen Prädiktors auf die abhängige Variable. Wir können Sie ähnlich wie Korrelationen interpretieren und so die Einflüsse der einzelnen Prädiktoren auf die abhängige Variable miteinander vergleichen. In unserem Beispiel hat also der Preis den größten Einfluss auf die Bewertung mit einem Regressionsgewicht von β = 0,541. Der Geschmack hat nur den zweitgrößten Einfluss mit einem Regressionsgewicht von β = 0,414.
Die letzten beiden Spalten geben Aufschluss, ob der jeweilige Prädiktor einen signifikanten Einfluss auf die abhängige Variable hat oder, ob wir doch eher von einem Zufall ausgehen sollten. Wird der entsprechende p-Wert signifikant (p<.05), können wir sagen, dass der Prädiktor die Produktbewertung unseres Burgers signifikant beeinflusst. Der Wert basiert auf einem t-Test für 1 Stichprobe, welcher die Hypothese testet, ob β in der Population gleich 0 ist (H0) oder nicht. Ist β gleich 0, dann hat sie keinen Einfluss auf die abhängige Variable. In unserem Beispiel besitzt z.B. der Prädiktor Aussehen keinen signifikanten Einfluss auf die Produktbewertung des Burgers.
Das folgende Video zeigt Ihnen die multiple Regression an einem weiteren Beispiel aus der FiveProfs Kette.
17.4 Multiple Regression | Erklärung des Modells an einem Beispiel
18.4 Modellgüte
Im letzten Abschnitt haben wir ein multiples Regressionsmodell aufgestellt. Was wir jedoch noch nicht wissen, ist, wie gut das Modell nun eigentlich ist. Diese Frage beantworten wir, indem wir die Gütekriterien betrachten. Diese geben uns Auskunft darüber, wie gut unsere Regressionsgleichung die abhängige Variable vorhersagen kann. Die Gütekriterien entsprechen dabei denen der bivariaten Regression aus Kapitel 5.
Determinationskoeffizient R2
Der Determinationskoeffizient R2 beschreibt, wie viel Varianz der abhängigen Variable durch die Prädiktoren im multiplen Regressionsmodell aufgeklärt werden kann. Die Werte reichen von 0 bis 1 und können in Prozentangaben ausgedrückt werden. Ein R2= .457 sagt aus, dass sich durch die Prädiktoren 45,7% der Varianz der abhängigen Variable aufklären lassen. Der Determinationskoeffizient ergibt sich, wenn wir die Modellvarianz durch die Gesamtvarianz teilen. Die restliche nicht aufgeklärte Varianz deutet auf Fehlervarianz hin, die beispielsweise durch nicht einbezogene Prädiktoren (z.B. persönliche Gemütslage) oder andere unsystematische Einflüsse entstehen kann.

F-Wert
Alternativ kann auch der F-Wert in Betracht gezogen werden. Dieser ergibt sich, wenn wir die Modellvarianz durch die Fehlervarianz teilen. Wir vergleichen somit wie gut das Modell ist, im Vergleich zu den Fehlern, die es macht. Hierbei sollte der F-Wert immer >1 sein.
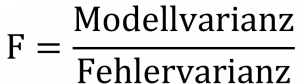
Um die Anwendung der Gütekriterien an einem Beispiel nochmal nachzuvollziehen, können Sie sich abschließend folgendes Video anschauen.
17.5 Multiple Regression | Modellgüte am Beispiel
13.7 Übungsfragen
Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!
In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!



