Multiple lineare Regression mit R

Patrick Planing

Statistik mit R & RStudio

30 Multiple lineare Regression mit R

Multiple lineare Regression

Eine multiple lineare Regression ist ein statistisches Verfahren, das zur Vorhersage des Wertes einer abhängigen Variablen (auch Kriterium genannt) auf der Grundlage der Werte einer oder mehrerer unabhängiger Variablen (auch Prädiktorvariablen genannt) verwendet wird. Die allgemeine Form der Gleichung für eine multiple lineare Regression ist

Y = b0 + b1X1 + b2X2 + … + bnXn,

wobei Y die abhängige Variable ist, X1, X2, … Xn die unabhängigen Variablen sind, und b0, b1, b2, … bn die Koeffizienten der Gleichung sind. Diese Koeffizienten werden mit der Methode der “gewöhnlichen kleinsten Quadrate” (OLS) geschätzt, die die Summe der quadrierten Residuen zwischen den vorhergesagten und tatsächlichen Werten der abhängigen Variable minimiert.

Beispiel

Wir wollen der Frage nachgehen, ob wir die Lebenszufriedenheit aus der Zufriedenheit mit dem Studium und der Zufriedenheit mit der Partnerschaft vorhersagen können und nutzen dazu wieder den WPStudis Datensatz.

Daten vorbereiten

Datensatz einlesen (Sie muessen natuerlich noch Ihren Pfad aendern)

load("WPStudis.RData")

Wir erstellen ein Subset mit den relevanten Variablen und schließen NAs aus:

data_multi <- WPStudis[c("F1_Nummer","F19_Partnerschaft","F21_01_Zufriedenheit_Leben","F21_02_Zufriedenheit_Studium","F21_03_Zufriedenheit_Partnerschaft")]

Wir schließen wieder fehlende Werte aus, da diese auch bei der multiplen Regression zu Problemen führen.

data_multi <- na.omit(data_multi)

Modell erstellen

In R können Sie mit der Funktion lm() eine multiple lineare Regression durchführen. Die grundlegende Syntax lautet:

model <- lm(Y ~ X1 + X2 + … + Xn, data = your_data)

Hier ist Y die abhängige Variable (Kriterium), und X1, X2, … Xn sind die unabhängigen Variablen (Prädiktoren). In unserem Fall sieht das Modell also wie folgt aus:

lm4<- lm(F21_01_Zufriedenheit_Leben ~ F21_02_Zufriedenheit_Studium + F21_03_Zufriedenheit_Partnerschaft , data=data_multi)
summary(lm4)
## 
## Call:
## lm(formula = F21_01_Zufriedenheit_Leben ~ F21_02_Zufriedenheit_Studium + 
##     F21_03_Zufriedenheit_Partnerschaft, data = data_multi)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.4732 -0.2084  0.0564  0.3647  1.3212 
## 
## Coefficients:
##                                    Estimate Std. Error t value
## (Intercept)                         2.19408    0.43483   5.046
## F21_02_Zufriedenheit_Studium        0.26479    0.09763   2.712
## F21_03_Zufriedenheit_Partnerschaft  0.19104    0.07884   2.423
##                                      Pr(>|t|)    
## (Intercept)                        0.00000253 ***
## F21_02_Zufriedenheit_Studium          0.00809 ** 
## F21_03_Zufriedenheit_Partnerschaft    0.01751 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.712 on 85 degrees of freedom
## Multiple R-squared:  0.1595, Adjusted R-squared:  0.1397 
## F-statistic: 8.063 on 2 and 85 DF,  p-value: 0.0006216

Das Ergebnis zeigt, dass sowohl die Zufriedenheit mit dem Studium, als auch die Zufriedenheit mit der Partnerschaft signifikante Prädiktoren für die Lebenszufriedenheit sind. Beide Prädiktoren haben einen P-Wert von < 0.05 (Spalte Pr(>|t|)).

Das Modell hat eine aufgeklärte Varianz von 0.14 (R2-Wert). Wir können mit den beiden Variablen zusammen, also rund 14 % der Varianz der Lebenszufriedenheit erklären. Der Rest wird wohl durch andere Faktoren bestimmt.

Voraussetzungen prüfen

Wir müssen natürlich noch die Voraussetzungen für die multiple Regression prüfen. Diese sind:

Korrekte Spezifikation des Modells
Normalverteilung der Residuen
Homoskedastizität
Ausreißer und einflussreiche Datenpunkte
Multikollinearität
Unabhängigkeit der Residuen

Auch bei multiplen Regressionen funktioniert die Diagnostik für die Voraussetzungen 1-4 über die plot() Funktion. Da dies dem Vorgehen im vorigen Kapitel entspricht, werden wir hierauf nicht mehr vertieft eingehen.

par(mfrow=c(2,2))    #4 Graphen pro Seite
plot(lm4)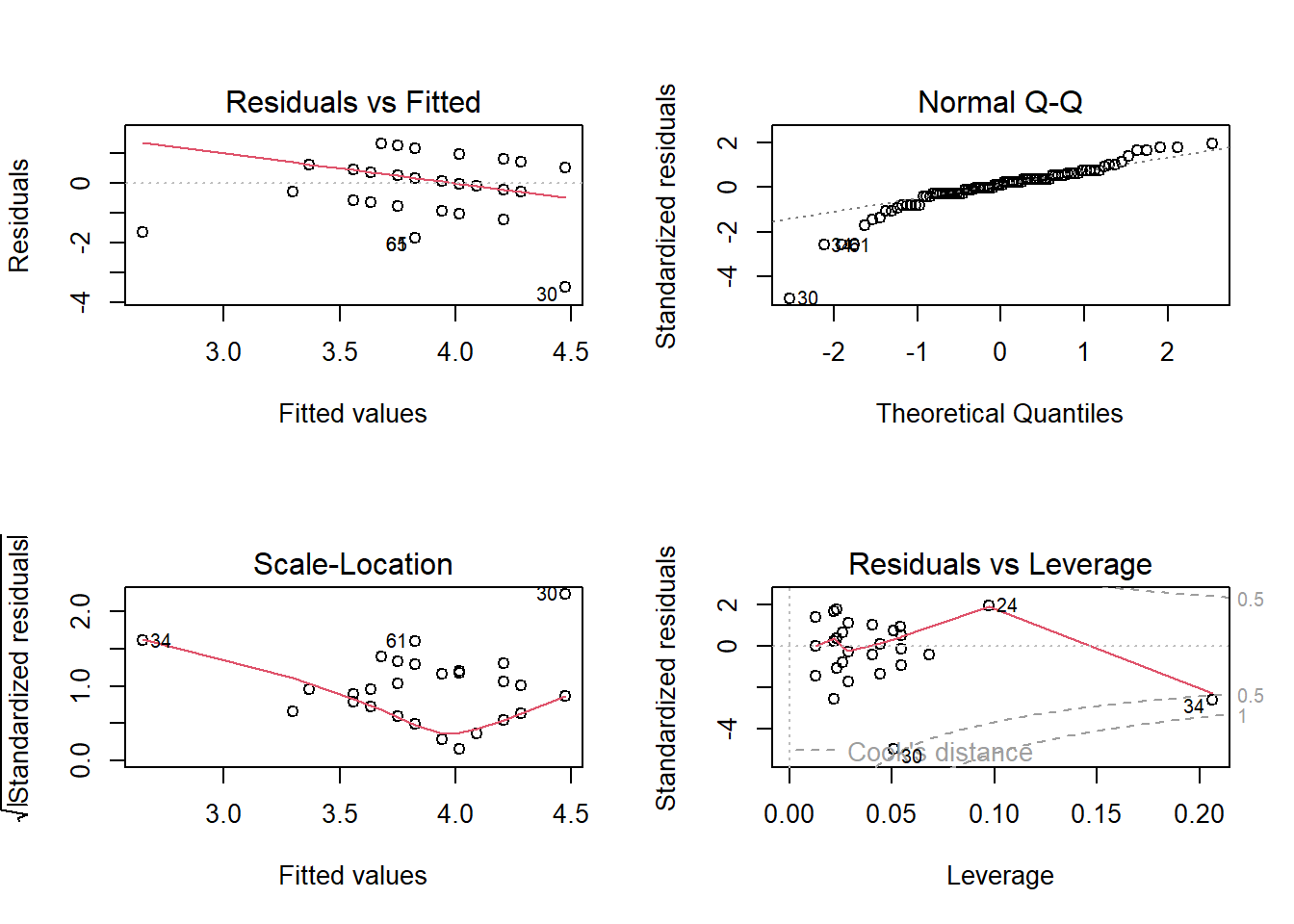

dev.off() #setzt das Layout zurueck
## null device 
##           1

Voraussetzung 5&6:

Test auf Multikollinearitaet

In R können Sie die Funktion vif() des Pakets car verwenden, um auf Multikollinearität in einem multiplen linearen Regressionsmodell zu testen.

Sobald Sie Ihr Modell haben, können Sie die Funktion vif() verwenden, um den Varianzinflationsfaktor (VIF) für jede unabhängige Variable zu berechnen. Der VIF ist ein Maß dafür, wie stark die Varianz des geschätzten Koeffizienten einer bestimmten unabhängigen Variablen aufgrund von Multikollinearität erhöht ist. Ein VIF von 1 bedeutet, dass keine Multikollinearität vorliegt, während ein VIF größer als 1 bedeutet, dass Multikollinearität vorliegt.

Wenn einer der VIF-Werte größer als 5 (je nach Literatur 10) ist, deutet dies darauf hin, dass diese Variable mit anderen unabhängigen Variablen korreliert ist und es besser ist, diese Variable aus dem Modell zu entfernen. Wenn alle VIF-Werte kleiner als 5 sind, bedeutet dies, dass keine Multikollinearität im Modell vorliegt.

library(car)
vif(lm4) 
##       F21_02_Zufriedenheit_Studium 
##                           1.033705 
## F21_03_Zufriedenheit_Partnerschaft 
##                           1.033705

In unserem Fall liegt also keine Multikollinearität vor. Um die Korrelation zwischen verschiedenen Variablen zu beurteilen, können wir alternativ zum VIF auch wieder auf die Streudiagramm-Matrix zurückgreifen

library(psych)
Zusammenhang <- data.frame(WPStudis$F21_02_Zufriedenheit_Studium,WPStudis$F21_03_Zufriedenheit_Partnerschaft)
pairs.panels(Zusammenhang)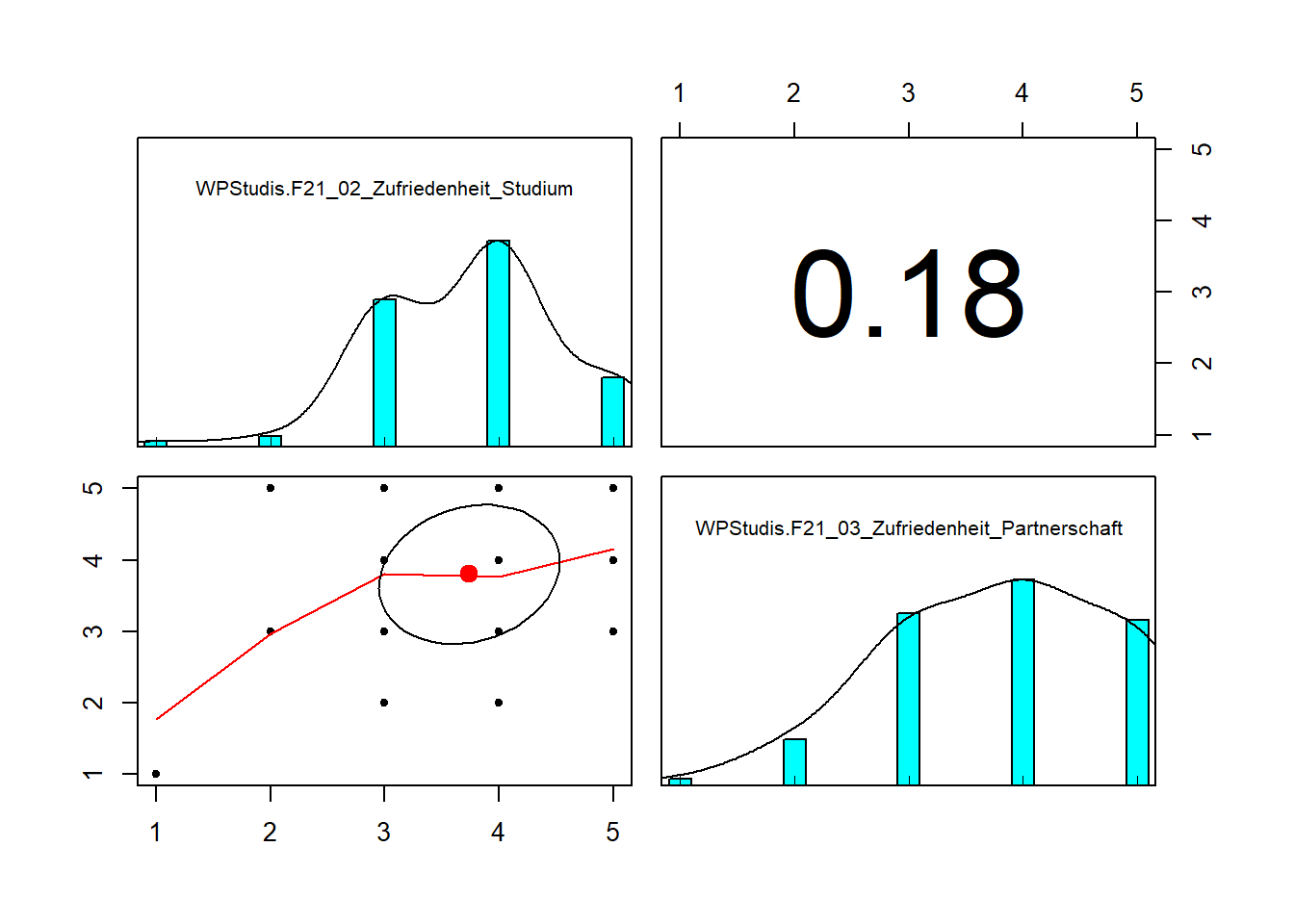

Auch hier sehen wir, dass die beiden Prädiktoren nur schwach korreliert sind.

Test auf Unabhängigkeit der Residuen

Eine weitere Voraussetzung ist die Unabhängigkeit der Residuen. Das bedeutet, dass die Residuen (Schätzfehler) nicht untereinander korrelieren sollten. Dies geschieht jedoch in der Praxis meist nur dann, wenn Zeitreihen vorliegen oder es sonst einen logischen Zusammenhang der Reihenfolge der Daten gibt.

Um dies zu prüfen, nutzen wir den Durbin-Watson-Test. Der Durbin-Watson-Test ist ein statistischer Test, der dazu dient, das Vorhandensein einer seriellen Korrelation (auch Autokorrelation genannt) in den Residuen eines linearen Regressionsmodells festzustellen. Eine serielle Korrelation liegt vor, wenn die Residuen eines Modells nicht unabhängig voneinander sind, was zu verzerrten und ineffizienten Schätzungen der Parameter des Modells führen kann.

Die Durbin-Watson-Teststatistik, die mit d bezeichnet wird, liegt zwischen 0 und 4. Ein Wert von 2 zeigt an, dass es keine serielle Korrelation in den Residuen gibt, während ein Wert von weniger als 2 auf eine positive serielle Korrelation hinweist (was bedeutet, dass auf Residuen mit größeren Größen tendenziell Residuen mit ähnlichen Größen folgen), und ein Wert von mehr als 2 auf eine negative serielle Korrelation hinweist (was bedeutet, dass auf Residuen mit größeren Größen tendenziell Residuen mit entgegengesetzten Vorzeichen folgen). Grundsätzlich sollte der Test also nicht signifikant werden und die Pruefstatistik sollte relativ nahe an 2 liegen.

In R können Sie den Durbin-Watson-Test mit der Funktion durbinWatsonTest() aus dem Paket car durchführen.

durbinWatsonTest(lm4)  
##  lag Autocorrelation D-W Statistic p-value
##    1      0.02084141      1.951871   0.796
##  Alternative hypothesis: rho != 0

In diesem Fall liegt also keine Autokorrelation vor und wir können mit der Interpretation fortfahren.

Modellvergleich

Grundsätzlich gilt beim multiplen Regressionsmodell das Gesetz der Sparsamkeit. Das bedeutet, dass nur weiter Prädiktoren in ein Modell aufgenommen werden sollten, wenn diese die Vorhersage des Modells auch signifikant verbessern. Um dies zu testen, kann man für die Aufnahme jedes Faktors einen Modellvergleich machen, um festzustellen, ob das Modell mit dem zusätzlichen Prädiktor eine signifikant bessere Vorhersage macht.

Dies können wir auch auf unser Beispiel von oben anwenden. Die Frage wäre hier zum Beispiel: Bringt das multiple Modell mit zwei Prädiktoren eine bessere Vorhersage, als wenn ich die Lebenszufriedenheit aus der Zufriedenheit mit der Partnerschafft alleine vorhersage?

Wer erstellen dazu ein “Konkurrenz-Modell” mit nur einem Prädiktor und nennen es “lm5”.

lm5<- lm(F21_01_Zufriedenheit_Leben ~ F21_03_Zufriedenheit_Partnerschaft, data=data_multi)
summary(lm5)
## 
## Call:
## lm(formula = F21_01_Zufriedenheit_Leben ~ F21_03_Zufriedenheit_Partnerschaft, 
##     data = data_multi)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.1857 -0.1857  0.0439  0.2736  1.2736 
## 
## Coefficients:
##                                    Estimate Std. Error t value
## (Intercept)                         3.03747    0.31498   9.643
## F21_03_Zufriedenheit_Partnerschaft  0.22965    0.08036   2.858
##                                               Pr(>|t|)    
## (Intercept)                        0.00000000000000241 ***
## F21_03_Zufriedenheit_Partnerschaft             0.00535 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.7379 on 86 degrees of freedom
## Multiple R-squared:  0.08673,    Adjusted R-squared:  0.07611 
## F-statistic: 8.167 on 1 and 86 DF,  p-value: 0.00535

Wir sehen, dass das Modell mit 2 Prädiktoren (oben) eine höhere aufgeklärte Varianz hat als dieses Modell (R2 0,14 vs 0,08). Da wir jedoch grundsätzlich sparsam sein sollten bei der Aufnahme weiterer Prädiktoren, prüfen wir nun, ob der Zugewinn an Varianz auch statistisch signifikant ist. Hierfür führen wir eine hierarchische Regression mit beiden Modellen durch. Dazu können wir die anova() Funktion nutzen, in die wir die zu vergleichenden Modelle eintragen. Der Syntax lautet dabei

anova(model1, model2)

Das Ergebnis F-Wert und den zugehörigen p-Wert für den Test der Nullhypothese, dass es keinen Unterschied in den Modellen gibt. Wenn der p-Wert kleiner ist als das von Ihnen gewählte Signifikanzniveau (z. B. 0,05), können Sie daraus schließen, dass ein signifikanter Unterschied zwischen den Modellen besteht.

Also in unserem Fall:

anova(lm5,lm4)
## Analysis of Variance Table
## 
## Model 1: F21_01_Zufriedenheit_Leben ~ F21_03_Zufriedenheit_Partnerschaft
## Model 2: F21_01_Zufriedenheit_Leben ~ F21_02_Zufriedenheit_Studium + F21_03_Zufriedenheit_Partnerschaft
##   Res.Df    RSS Df Sum of Sq     F   Pr(>F)   
## 1     86 46.826                               
## 2     85 43.096  1    3.7296 7.356 0.008088 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Die ANOVA wird signifikant und sagt uns damit, dass der Zugewinn an aufgeklärter Varianz statistisch signifikant ist. Wir sollten daher mit dem multiplen Modell mit zwei Prädiktoren weiter arbeiten.

In diesem Video zeige ich, wie das in R funktioniert:

Übung

Wir nutzen wieder den Prestige Datensatz. Wir wollen nun das Einkommen ´(“income”) wieder aus dem Bildungsgrad (“education”) vorhersagen, wollen aber als
weitere Prädiktoren das Prestige (“prestige”) des Jobs und den Frauenanteil (“women”) im Job dazunehmen. Erzeugen Sie das Regressionsmodell.

Wie hat sich der “Goodness of Fit” des Modells verändert?
Wie interpretieren Sie die Regressionsgewichte?

Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.