Statistik mit R & RStudio
22 Grafiken mit R
Grafiken mit der plot() Funktion
Vorbereitung
Datensatz ‘WPStudis.RData’ öffnen (Sie muessen ggf. noch Ihren Pfad aendern bzw. den Workspace neu definieren):
load("WPStudis.Rdata")Die plot() Funktion
Die Funktion plot() kann verwendet werden, um je nach Dateneingabe eine breite Palette von Diagrammen zu erstellen. Die folgende Tabelle gibt eine kleine Übersicht:
| Datenformat | Grafik |
|---|---|
| plot(vektor) | Index-Diagramm |
| plot(faktor) | Säulendiagramm |
| plot(vektor, vektor) | Streudiagramm |
| plot(faktor, vektor) | Boxplots |
| plot(faktor, faktor) | Mosaik-Diagramm |
| plot(dataframe) | Streu-Matrix |
Wenden wir die plot() Funktion zunächst auf einen Faktor an, dann erhalten wir ein Säulendiagramm.
plot(WPStudis$F3_Geschlecht)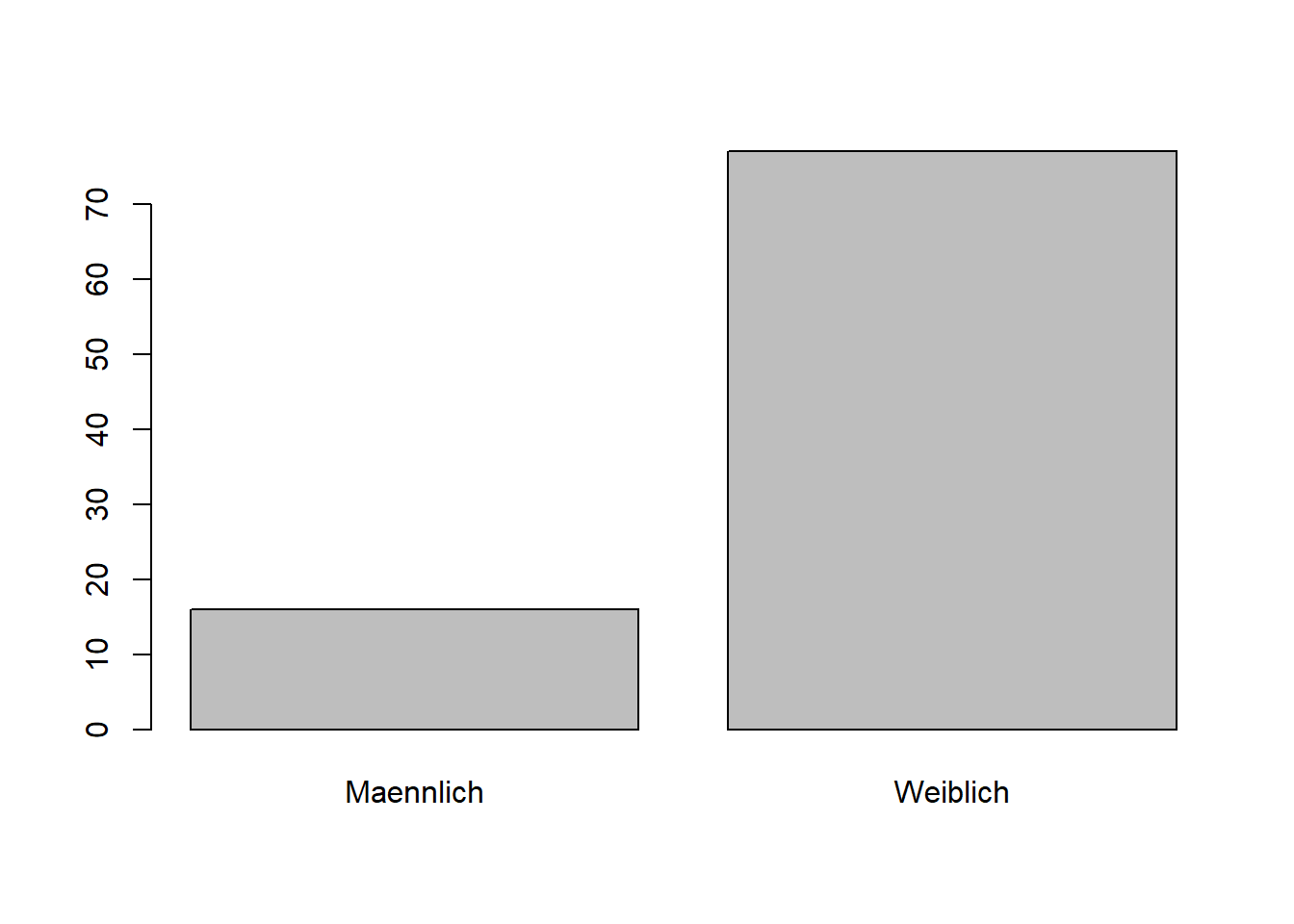
Die y-Achse könnte einen Tick höher sein. Dies lässt sich recht einfach mit dem ylim Argument ändern. Hier müssen zwei Werte mit der c() Funktion verbunden werden: Der Anfang und das Ende der y-Achse. Hier wollen wir eine Achse, die bei 0 anfängt und bis 100 geht.
plot(WPStudis$F3_Geschlecht, ylim=c(0,100))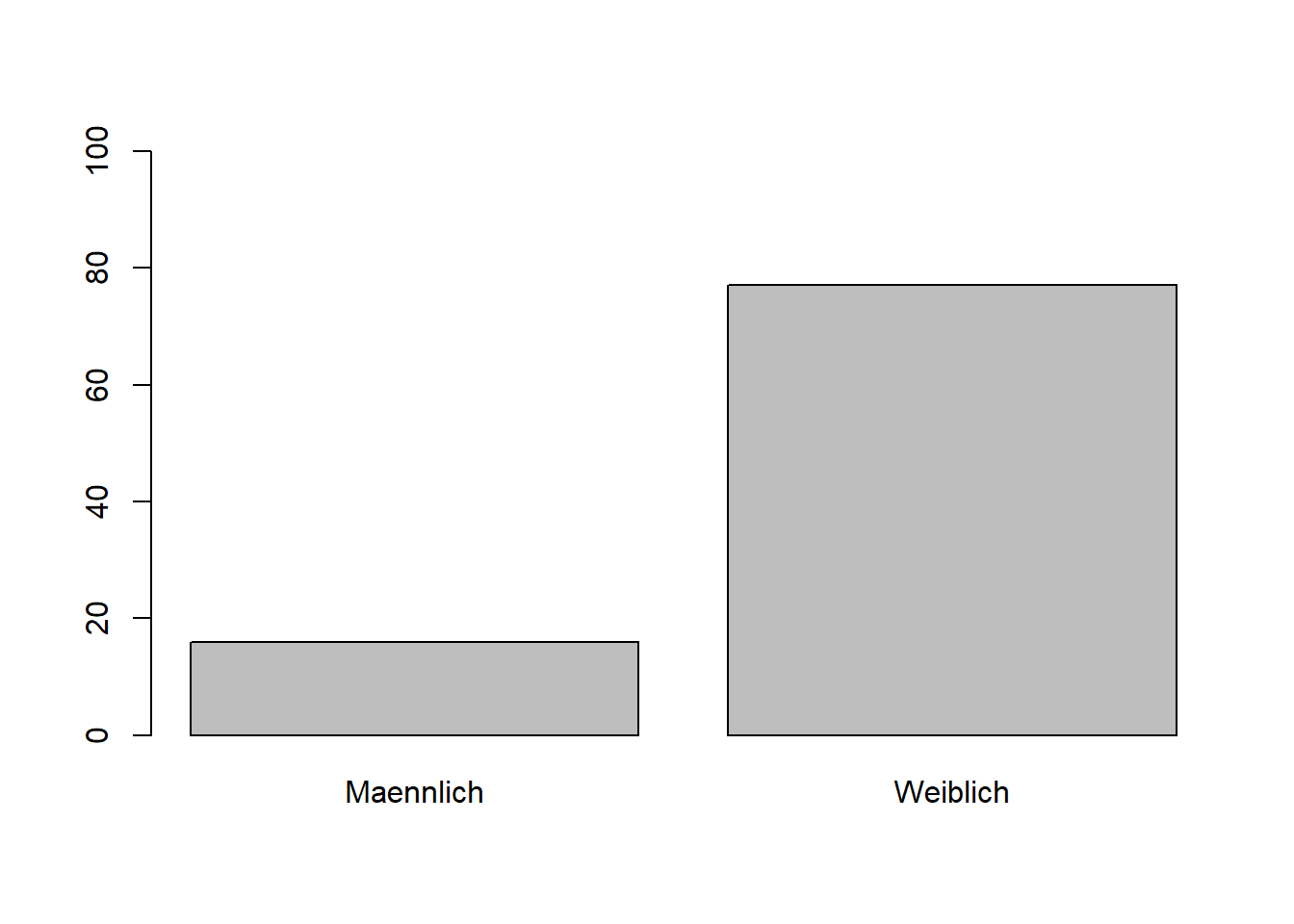
Mit dem Argument col lässt sich die Farbe der Säulen beispielsweise auf rot (“red”) ändern.
plot(WPStudis$F3_Geschlecht, ylim=c(0,100), col="red")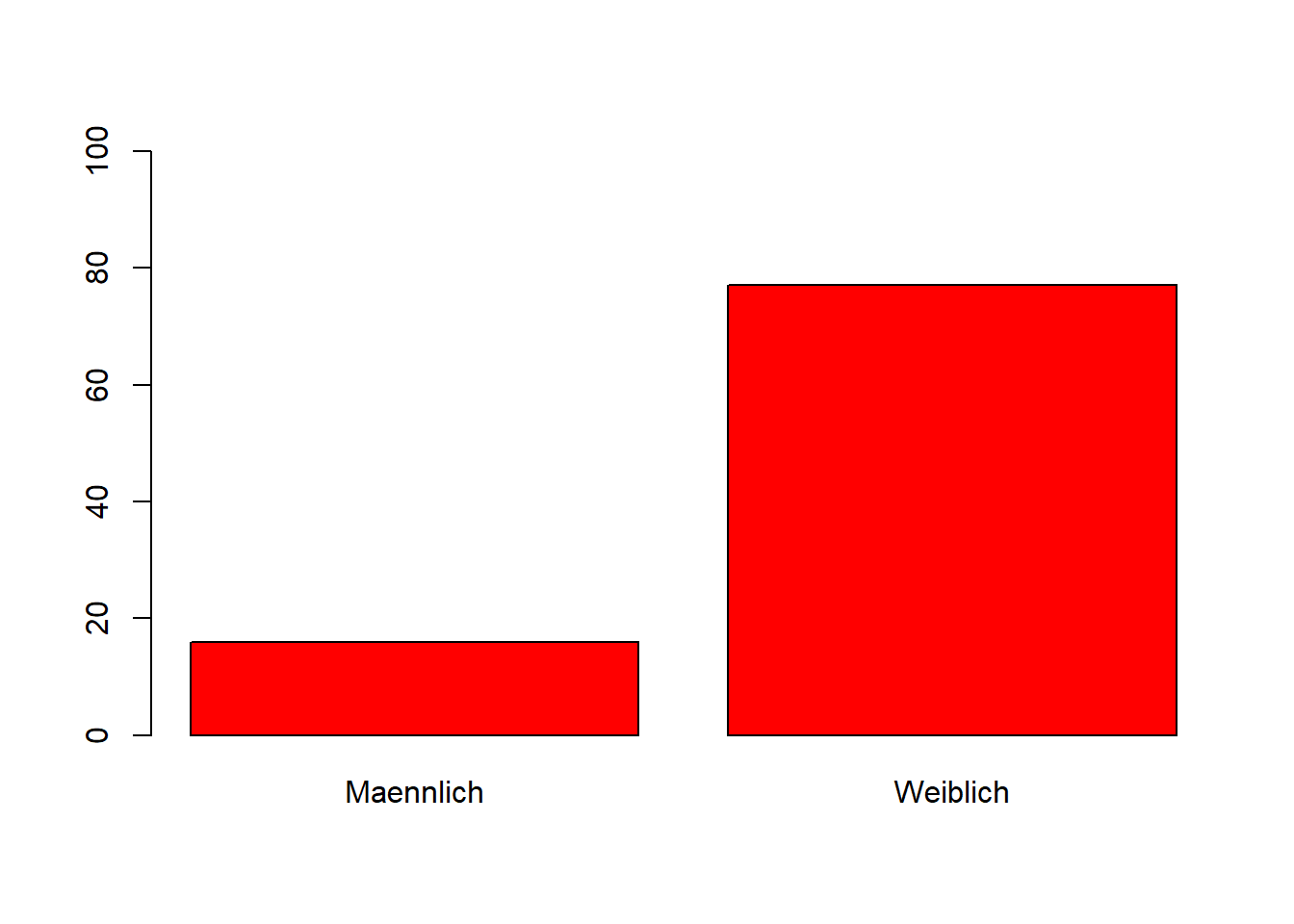
Es gibt auch andere Farben. Eine Übersicht über die in R mit Namen verfügbaren Farben erhält man mit dem Befehl colors(). Darüber hinaus gibt es jede mögliche RGB Farbe. Der Befehl hierfür ist col= gefolgt von einem Hashtag und dem 6-stelligen RGB Code der Farbe, also zum Beispiel col=“#009999”.
plot(WPStudis$F3_Geschlecht, ylim=c(0,120), col="#009999")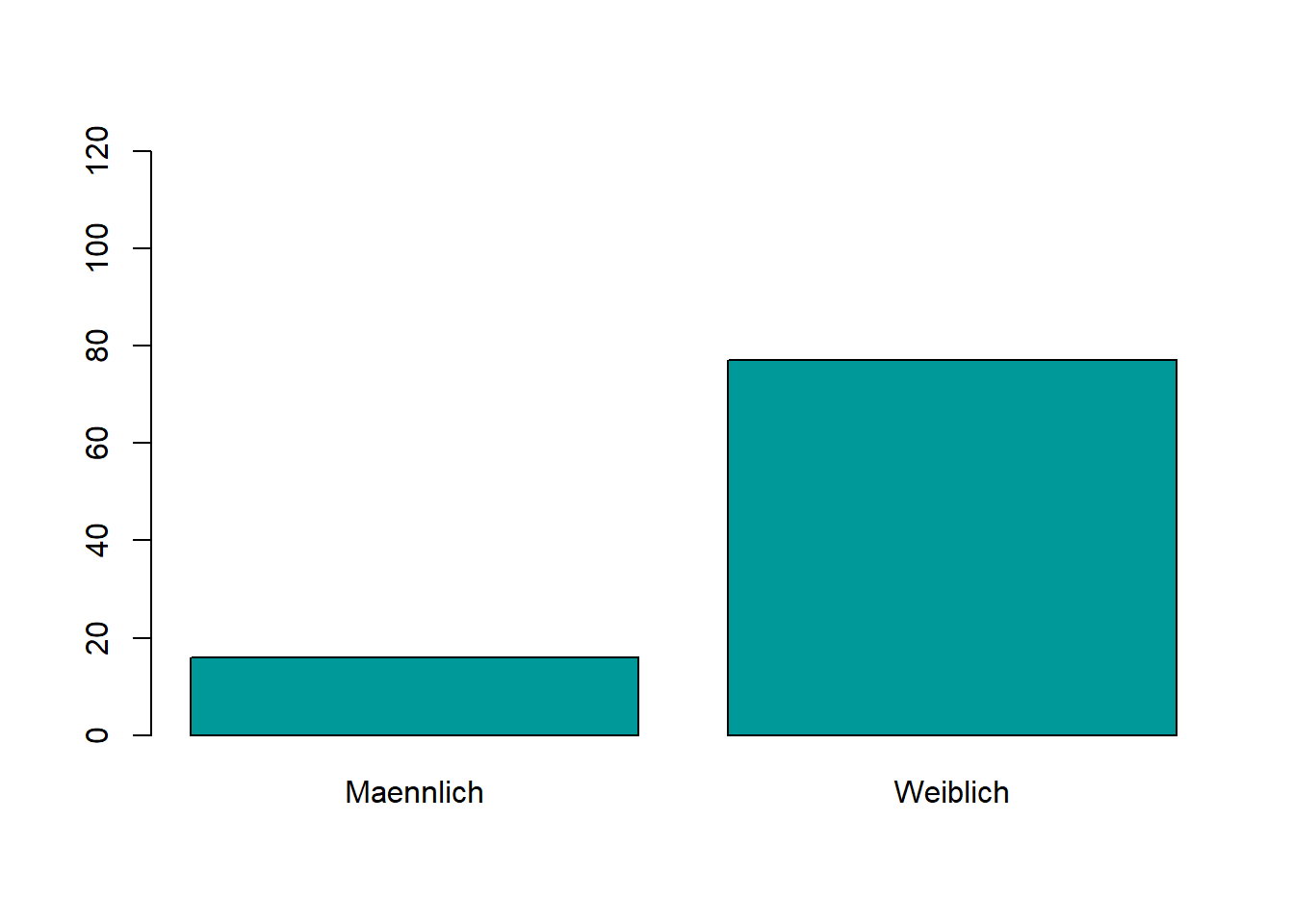
Wenn wir numerische Daten haben, dann gibt der Befehl ein Streudiagramm aus. Dies ist eine wenig sinnvolle Darstellungsform, wenn die Reihenfolge der Daten keine Rolle spielt (wie in unserem Datensatz). Die x-Achse entspricht dabei der Zeilennummer im Datensatz.
plot(WPStudis$F4_Koerpergroesse)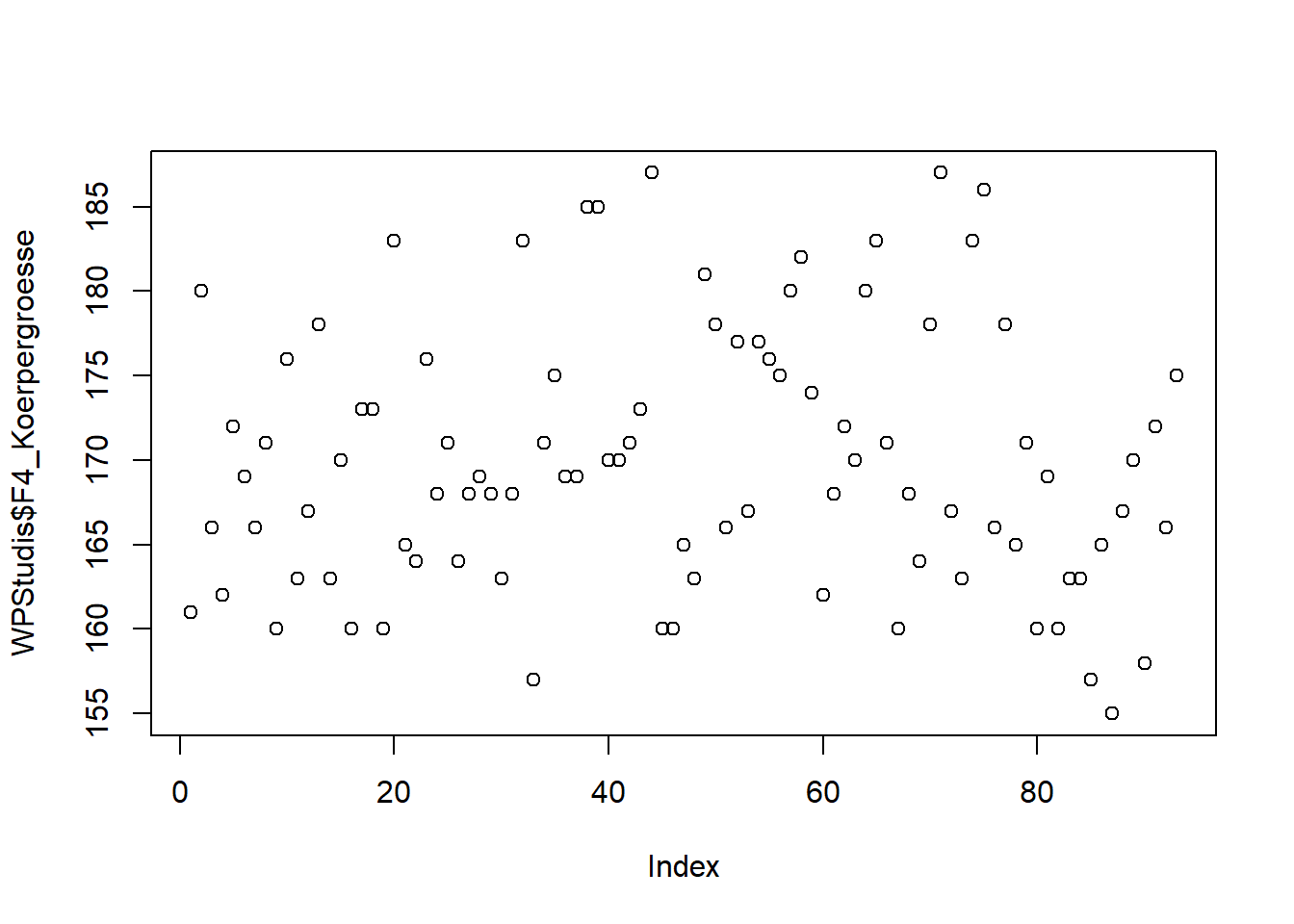
Bei zwei numerischen Variablen (Vektoren) macht eine solche Darstellung schon mehr Sinn. Bei zwei Variablen zeigt ein Streudiagramm den Zusammenhang der beiden Variablen in übersichtlicher Form. Hierfür benutzen wir die Tilde “~”. Es gilt y-Achse ~ x-Achse.
plot(WPStudis$F4_Koerpergroesse~WPStudis$F5_Schuhgroesse)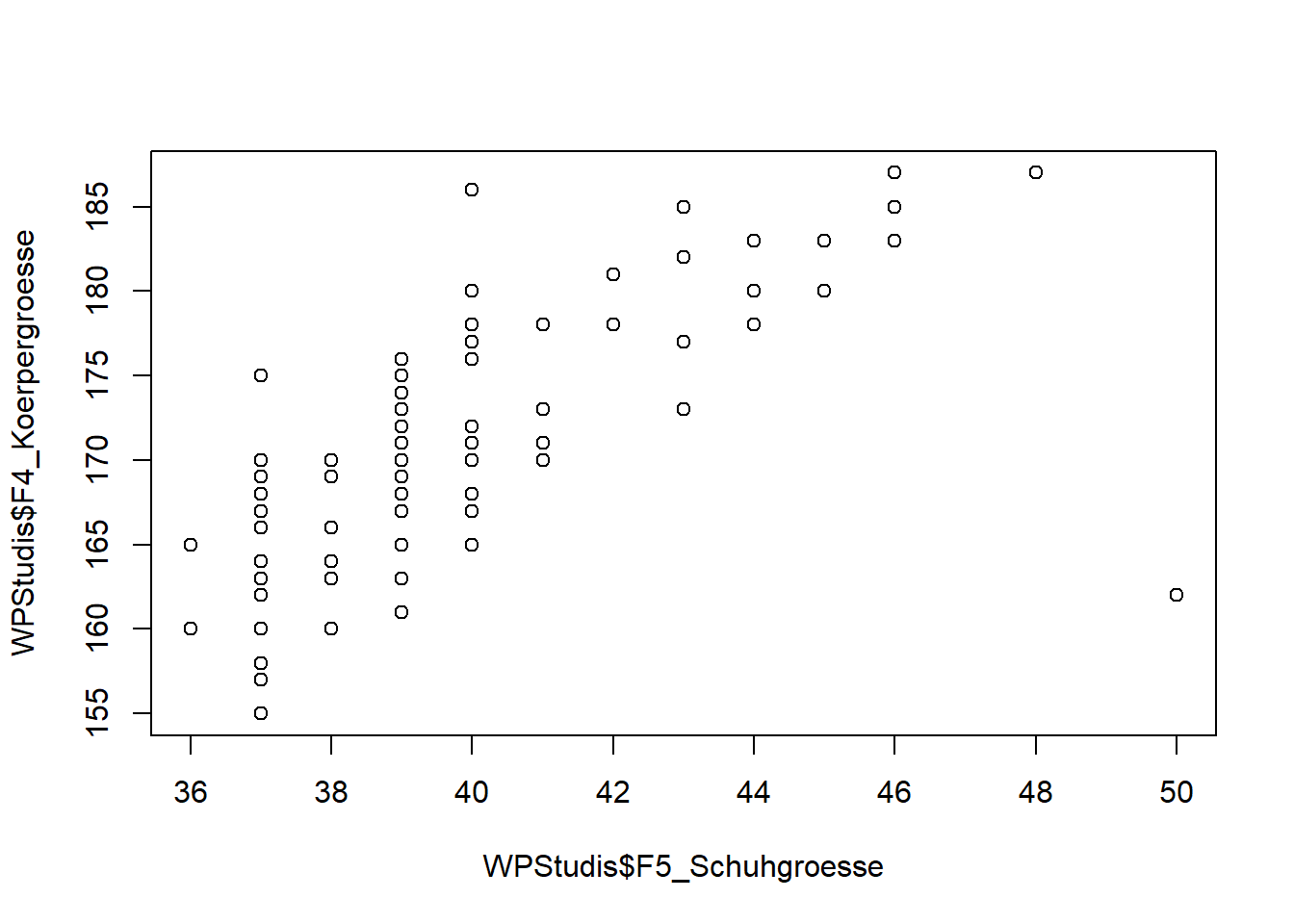
Falls eine Variable numerisch ist und die zweite Variable ein Faktor, bekommen wir mit demselben Befehl einen Boxplot. Hierzu nutzen wir nun die Variable Geschlecht, die als Faktor formatiert ist.
plot(WPStudis$F4_Koerpergroesse~WPStudis$F3_Geschlecht)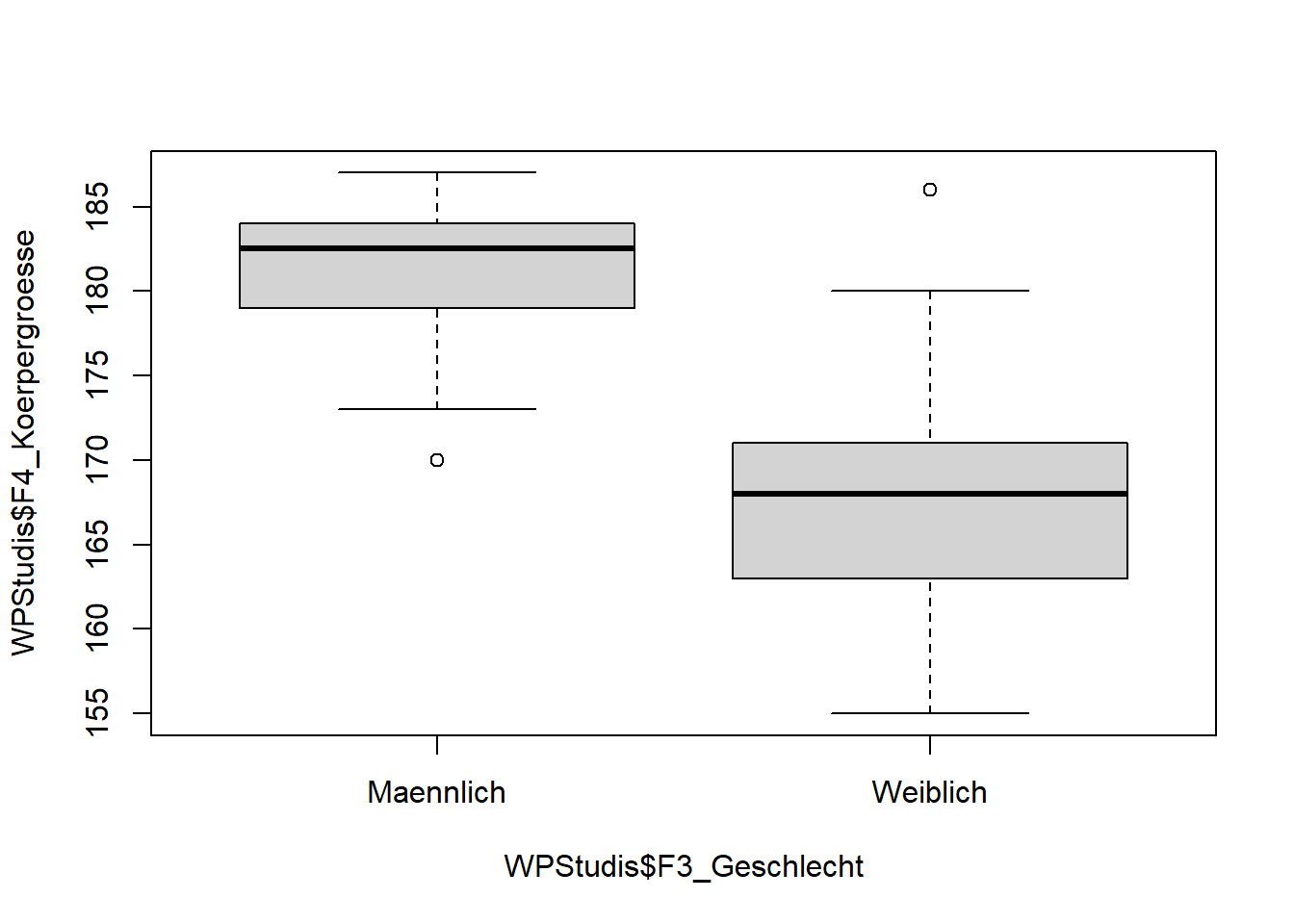
Falls beide Variablen Faktoren sind, bekommen wir mit demselben Befehl ein Mosaik-Diagramm. Dies entspricht einem gestapelten Balkendiagramm, wobei die Breite der Balken (x-Ausdehnung) dem jeweiligen relativen Anteil der Variable entspricht.
WPStudis$F21_01_Zufriedenheit_Leben<-as.factor(WPStudis$F21_01_Zufriedenheit_Leben)
plot(WPStudis$F21_01_Zufriedenheit_Leben ~ WPStudis$F3_Geschlecht)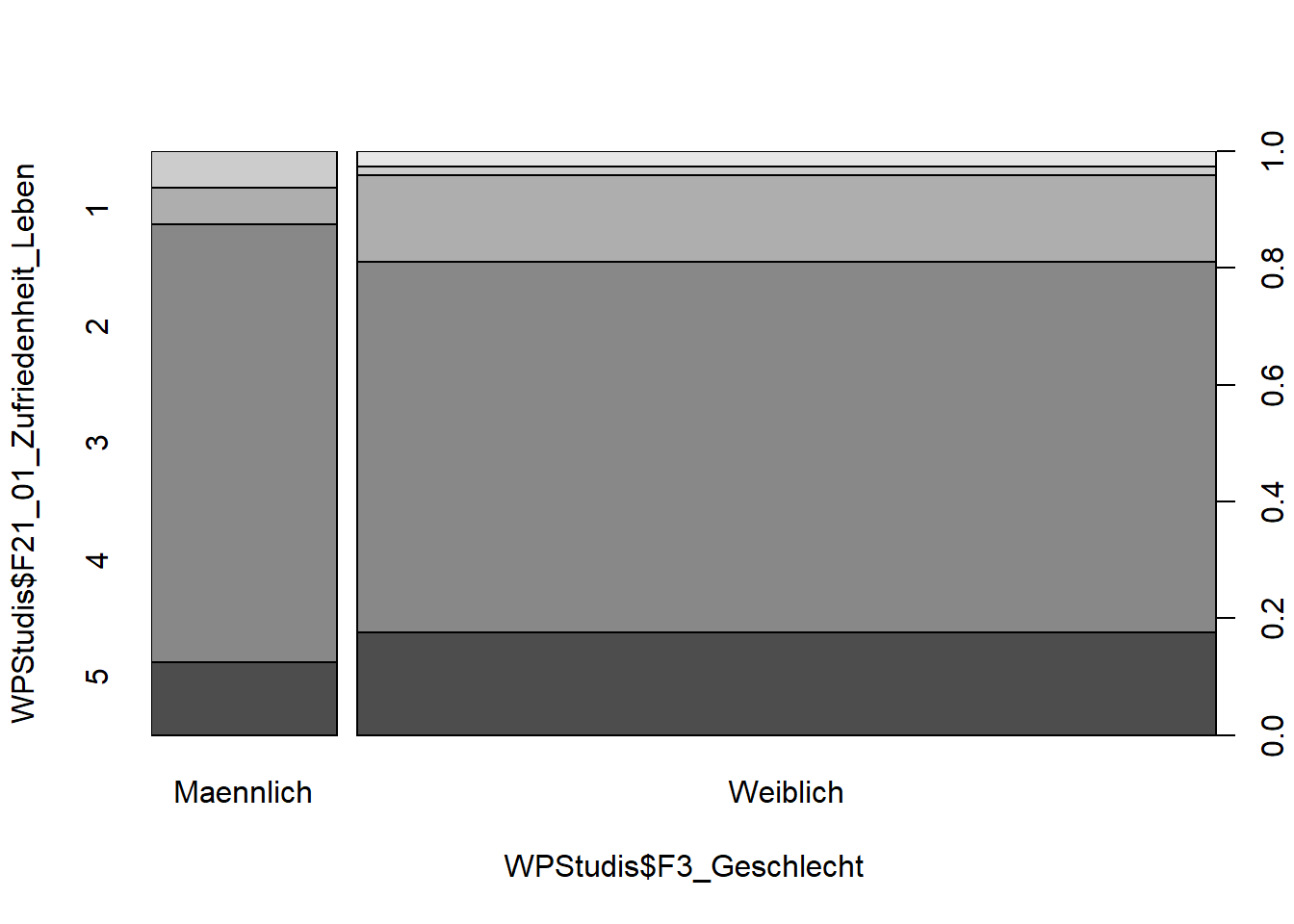
Weitere Möglichkeiten der Grafikgestaltung
Es gibt noch eine große Anzahl weiterer Argumente für die plot() Funktion, wie zum Beispiel:
-main: der Haupttitel des Diagramms.
-xlab: die Beschriftung für die x-Achse.
-ylab: die Beschriftung für die y-Achse.
Weitere Funktionen können Sie mit?plot() herausfinden.
Hier nochmal die gleiche Grafik, jedoch angereichert um die Beschriftungen der Achsen. xlab und ylab bezeichnen jeweils die Achsen-Beschriftungen (Label). main gibt den Diagramm-Titel an.
plot(WPStudis$F21_01_Zufriedenheit_Leben ~ WPStudis$F3_Geschlecht,
xlab = "Geschlecht",
ylab = "Zufriedenheit mit dem Leben",
main = "Zufriedenheit der Studierenden nach Geschlecht")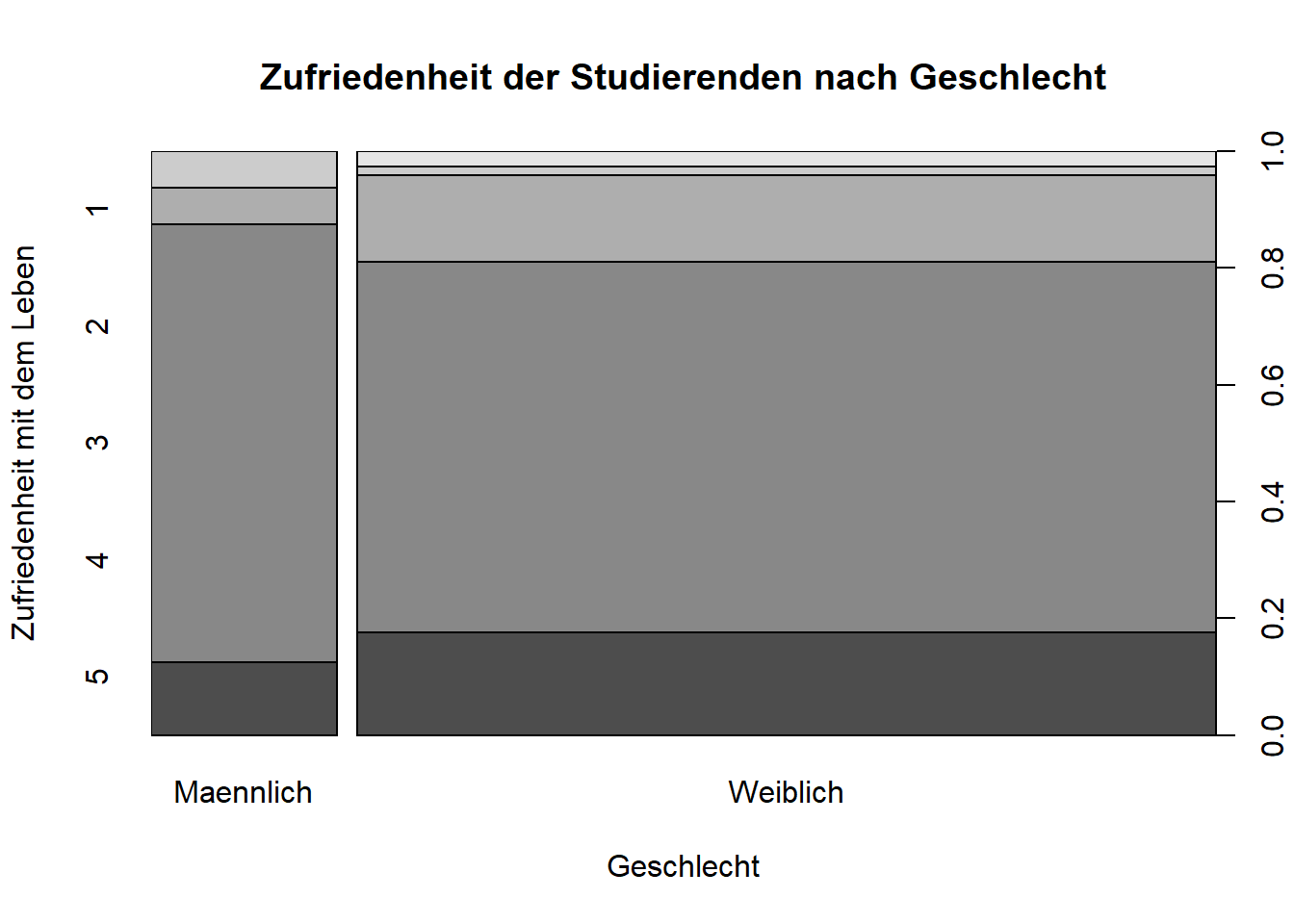
In diesem Video zeige ich, wie das in R funktioniert:
Weitere Grafiktypen mit R
Balkendiagramm
Um ein Balkendiagramm in R zu erstellen, können Sie die Funktion barplot() verwenden. Wichtig ist, dass wir diese Funktion auf Häufigkeiten anwenden, die wir mit der table() Funktion generieren. Nehmen wir an, wir wollen die Häufigkeiten der Antworten bei der Frage “Zufriedenheit mit dem Leben” darstellen.
barplot(table(WPStudis$F21_01_Zufriedenheit_Leben))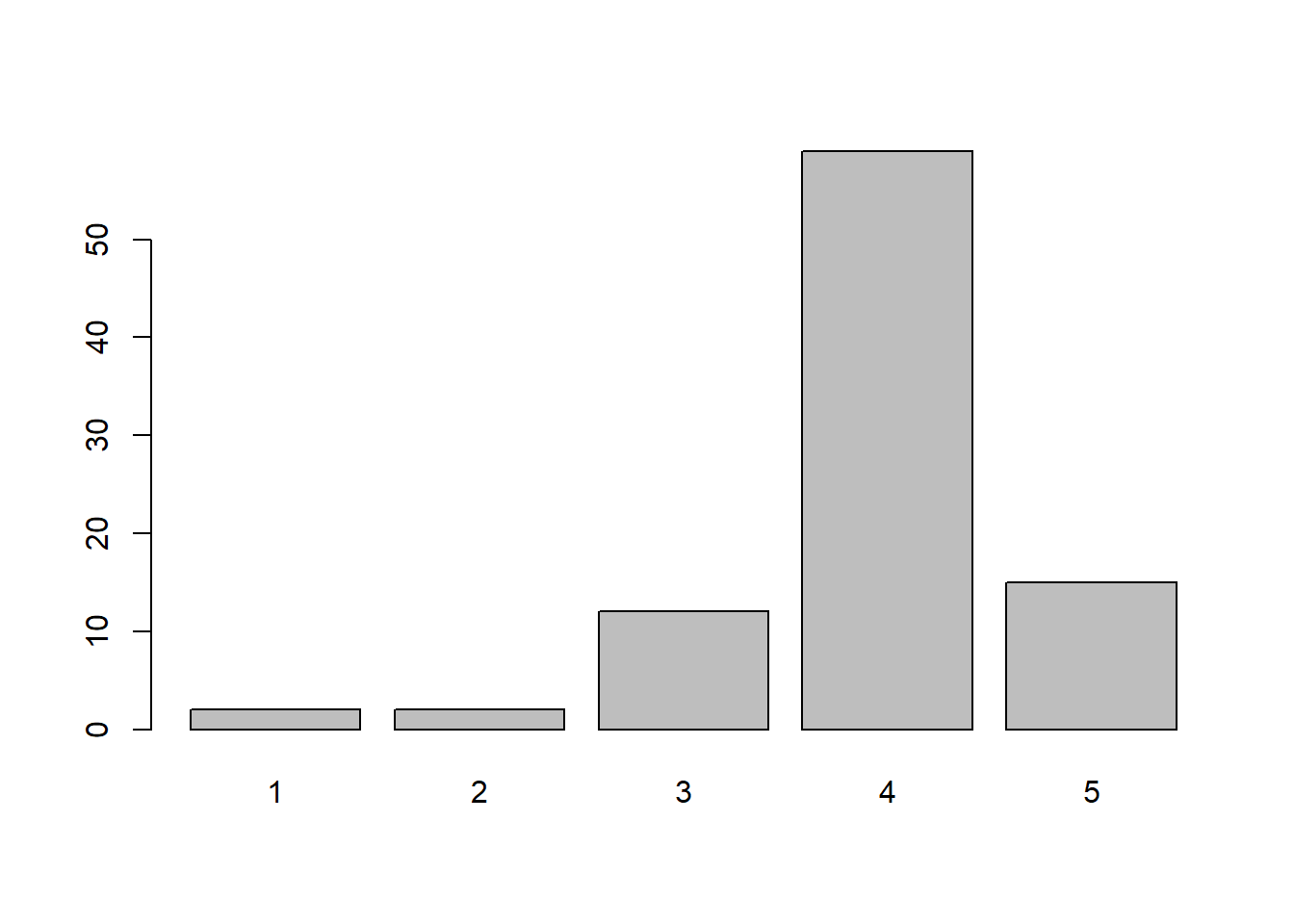
Nun wollen wir dies getrennt nach Geschlechtern dargestellt haben. Wir nutzen dazu die Kreuztabelle mit der prop.table() Funktion mit dem Parameter ,2 für die Spaltenprozente. In diesem Fall erhalten wir ein gestapeltes Balkendiagramm. Ein gestapeltes Balkendiagramm wird verwendet, um Vergleiche zwischen Datenkategorien zu zeigen, aber mit dem Zusatz, dass die Balken, die verschiedene Unterkategorien darstellen, übereinander gestapelt werden. Dies ermöglicht die Darstellung der Gesamtgröße jeder Kategorie sowie des Anteils jeder Unterkategorie an dieser Gesamtgröße.
barplot(prop.table(table(WPStudis$F21_01_Zufriedenheit_Leben,WPStudis$F3_Geschlecht),2))
Um die einzelnen Kategorien zuordnen zu können, benötigen wir noch eine Legende. Diese können wir uns mit Legend=True anzeigen lassen.
barplot(prop.table(table(WPStudis$F21_01_Zufriedenheit_Leben,WPStudis$F3_Geschlecht),2),legend=T)
Es ist wichtig zu beachten, dass gestapelte Balkendiagramme irreführend sein können, wenn man versucht, die Größe einzelner Unterkategorien über verschiedene Kategorien hinweg zu vergleichen, da die Stapel die zugrunde liegenden Werte verdecken können. In solchen Fällen kann es sinnvoller sein, ein gruppiertes Balkendiagramm zu verwenden, in dem die Balken für jede Unterkategorie nebeneinander angeordnet sind. Mit dem Argument beside=TRUE sorgt man dafür, dass statt gestapelten Balken, diese nebeneinander dargestellt werden und wir somit ein gruppiertes Balkendiagramm erhalten.
barplot(prop.table(table(WPStudis$F21_01_Zufriedenheit_Leben,WPStudis$F3_Geschlecht),2),beside=T,legend=T)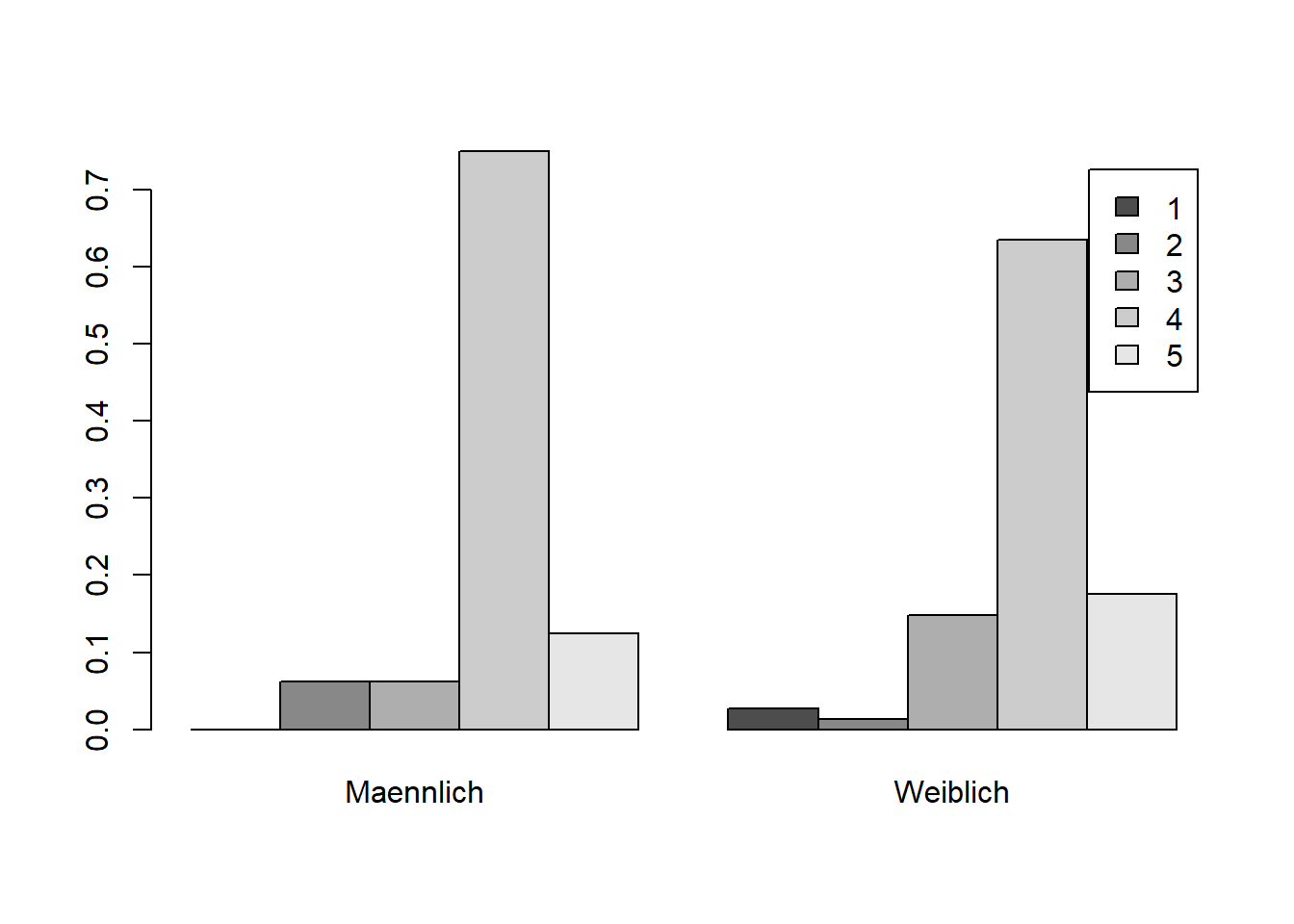
Hier ein Beispiel aus dem R Standarddatensatz VADeaths. Dieser enthält die Todesraten (pro 1000 Einwohner) im Bundesstaat Virginia, USA, in den Jahren 1907-1916.
Erzeugen wir zunächst ein einfaches Balkendiagramm.
barplot(VADeaths)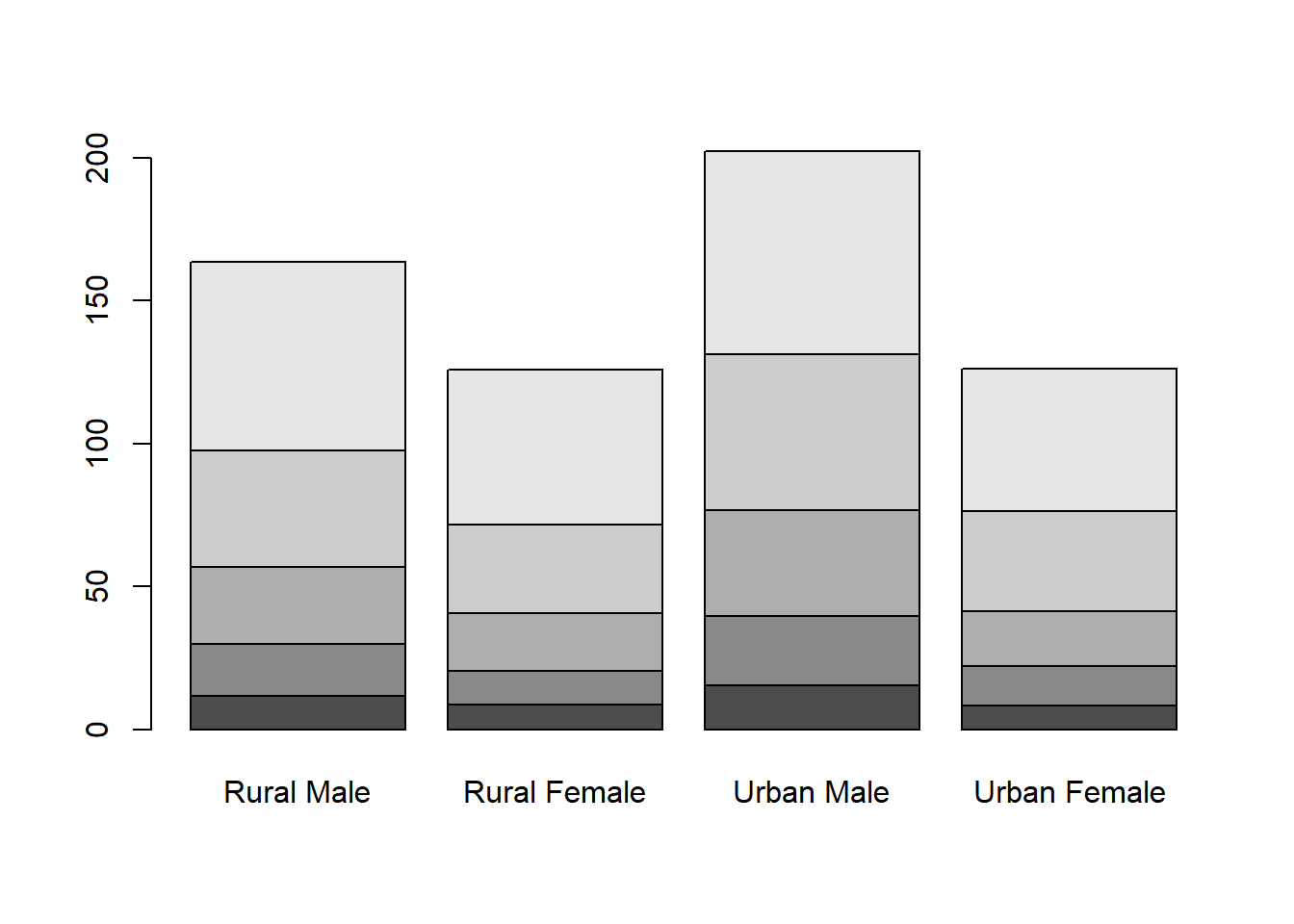
Die Lesbarkeit ist aufgrund der vielen Kategorien nicht optimal. Daher nun als gruppiertes Balkendiagramm mit dem Befehl beside=TRUE . Zusätzlich vergeben wir eine Überschrift und beschriften die y-Achse .
barplot(VADeaths, beside=TRUE, legend=TRUE, ylim=c(0,250),
ylab="Tote pro 1000",
main="Sterberaten in Virginia 1940")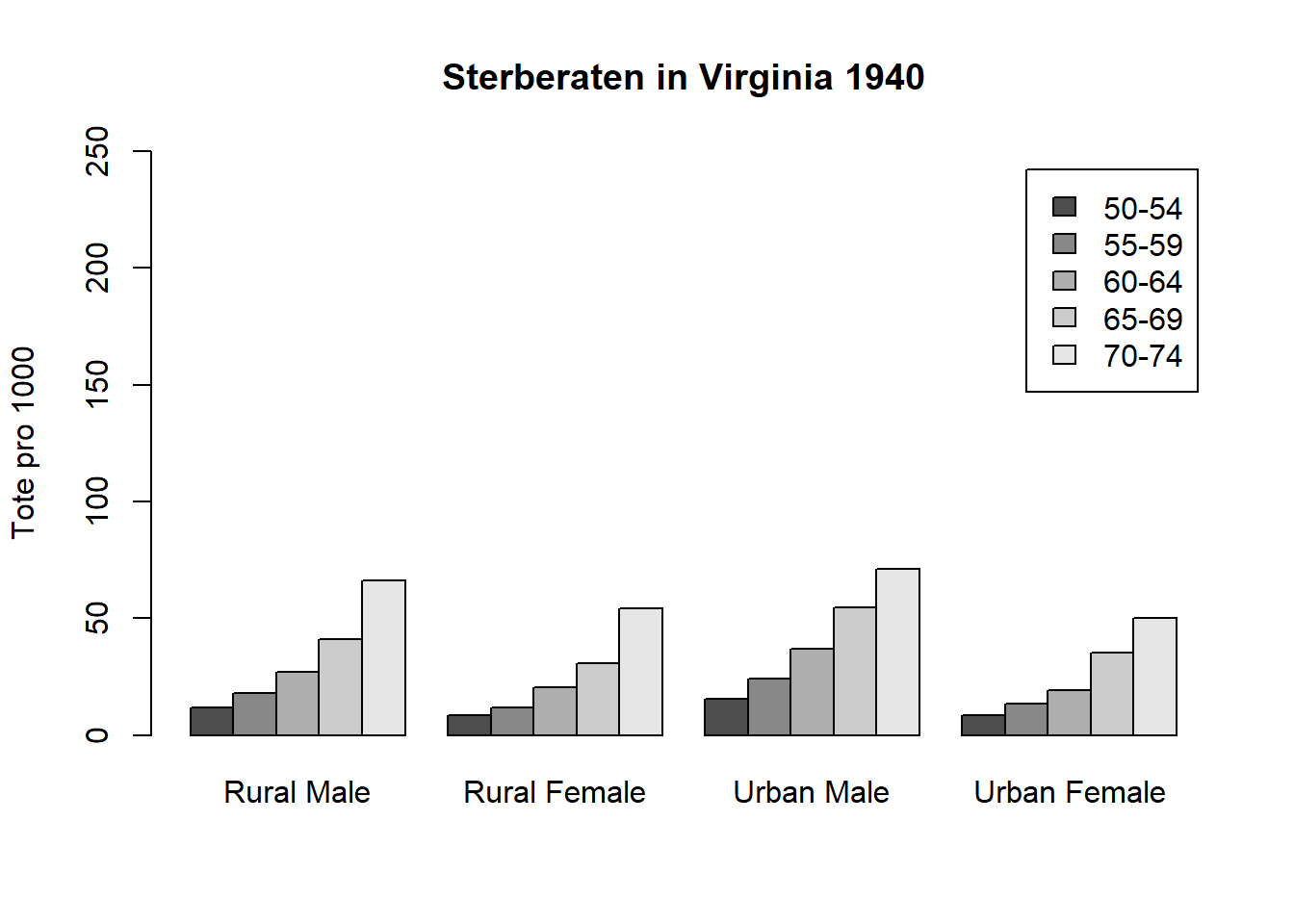
In diesem Video zeige ich, wie das in R funktioniert:
Übung
- Entwerfen Sie ein Balkendiagramm für die Schuhgroesse der WP Studierenden.
- Versuchen Sie die Balken rot und ohne Umrandung zu formatieren.
- Wenn Sie die Beschriftung der x-Achse betrachten, was fällt Ihnen auf? Welche alternative Darstellung könnte man für die Daten wählen?
Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.
Vergleich von Mittelwerten
Auch Mittelwerte lassen sich als Balkendiagramm darstellen. Hierfür wenden wir die barplot Funktion einfach auf den tapply Befehl aus dem vorangegangenen Kapitel an. Sie können mit dem Befehl col übrigens auch zwei Farbwerte angeben.
barplot(tapply(WPStudis$F4_Koerpergroesse,WPStudis$F3_Geschlecht, mean), ylim=c(0,200), col=c("#665588","#009999"))
Jedoch sind Balkendiagramme nicht der beste Weg, um zwei Mittelwerte grafisch zu vergleichen, da sie leicht zu einer Fehlinterpretation der Daten führen können. Beim Vergleich von zwei Mittelwerten kann der Höhenunterschied zwischen den Balken gering sein, was einen visuellen Vergleich der beiden Mittelwerte erschwert. Außerdem gibt die Höhe der Balken keinen Aufschluss über die Streuung der Daten oder die Variabilität innerhalb jeder Gruppe (Die Streuung liegt ja auch zu 50 % über den Balken, was allerdings optisch so nicht erkennbar ist).
Ein weiteres Problem bei Balkendiagrammen ist, dass sie keinen Hinweis auf die Unsicherheit um die Mittelwerte geben, wie z. B. die Standardabweichung oder das Konfidenzintervall. Dies bedeutet, dass es schwierig ist festzustellen, ob der Unterschied zwischen den beiden Mittelwerten statistisch signifikant ist.
Aus diesen Gründen werden Punktdiagramme oder sogenannte Fehlerbalkendiagramme als bessere Möglichkeiten für den grafischen Vergleich zweier Mittelwerte angesehen. Diese schauen wir uns im nächsten Kapitel an.
In diesem Video zeige ich, wie das in R funktioniert:
Fehlerbalkendiagramme
Mit dem psych Paket lassen sich sehr einfach Grafiken für Mittelwerte und Fehlerbalkendiagramme mit Konfidenzintervallen erstellen.
Hierzu nutzen wir die error.bars.by() Funktion des Pakets psych. Diese Funktion kann verwendet werden, um Fehlerbalken zu einem mit der Funktion barplot() erstellten Balkendiagramm hinzuzufügen, indem der Mittelwert und die Standardabweichung (oder der Standardfehler) für jede Gruppe angegeben werden.
Wollen wir zum Beispiel die Mittelwerte der Körpergröße von Frauen und Männern vergleichen, gehen wir wie folgt vor: error.bars.by(Variable1,Variable2). Hinweis: Standardmäßig zeigt die Funktion sogenannte Katzenaugen. Wenn Sie stattdessen die Fehlerbalken erhalten wollen, müssen Sie also eyes=FALSE angeben.
library(psych)
error.bars.by(WPStudis$F4_Koerpergroesse, WPStudis$F3_Geschlecht, eyes=FALSE)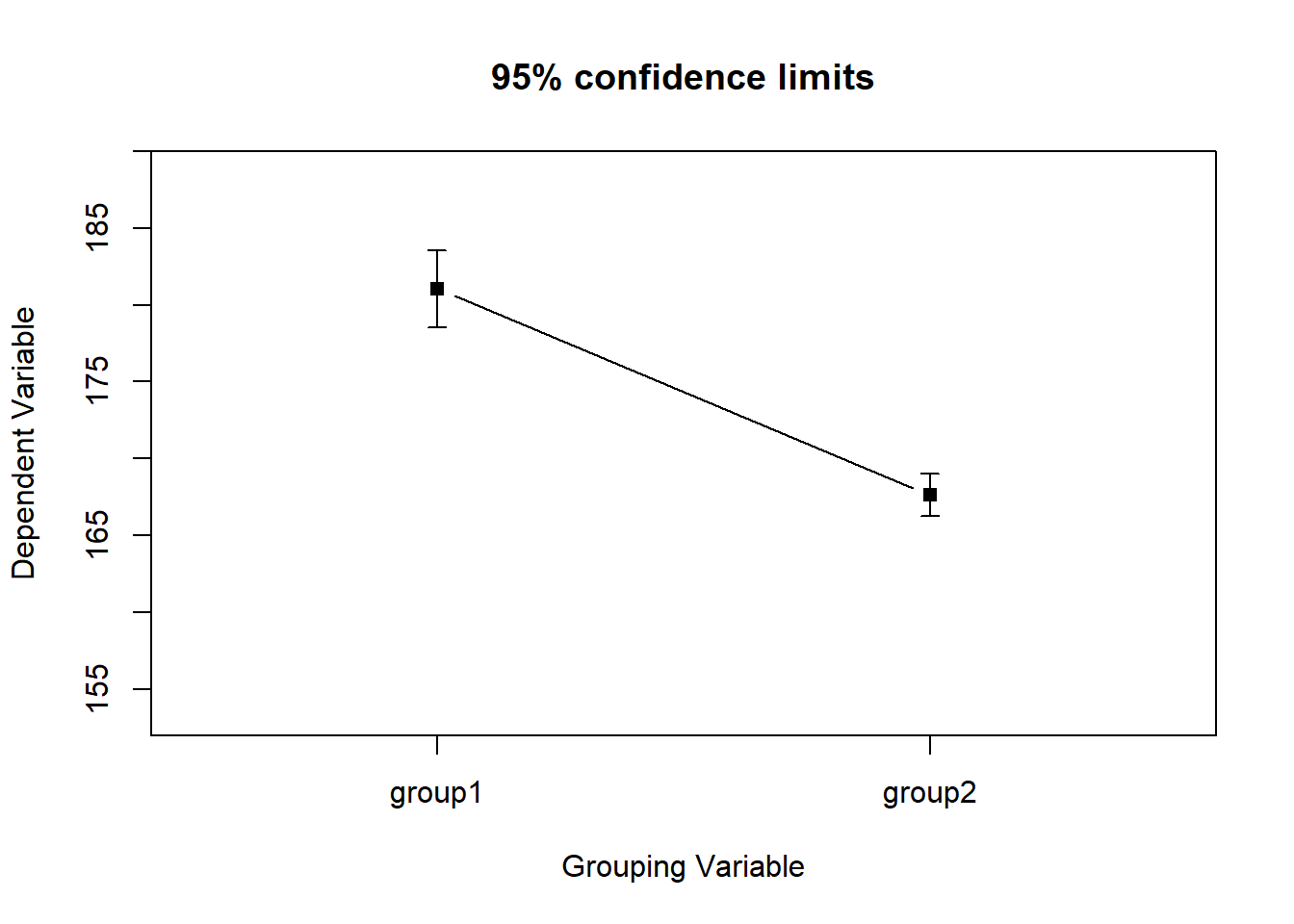
Leider benennt die Funktion die Gruppen immer mit “group1” etc., daher vergeben wir wieder die richtigen Labels mit der v.labels Funktion (für Variablen-Labels).
error.bars.by(WPStudis$F4_Koerpergroesse, WPStudis$F3_Geschlecht, eyes=FALSE, v.labels=cbind("Männlich","Weiblich"))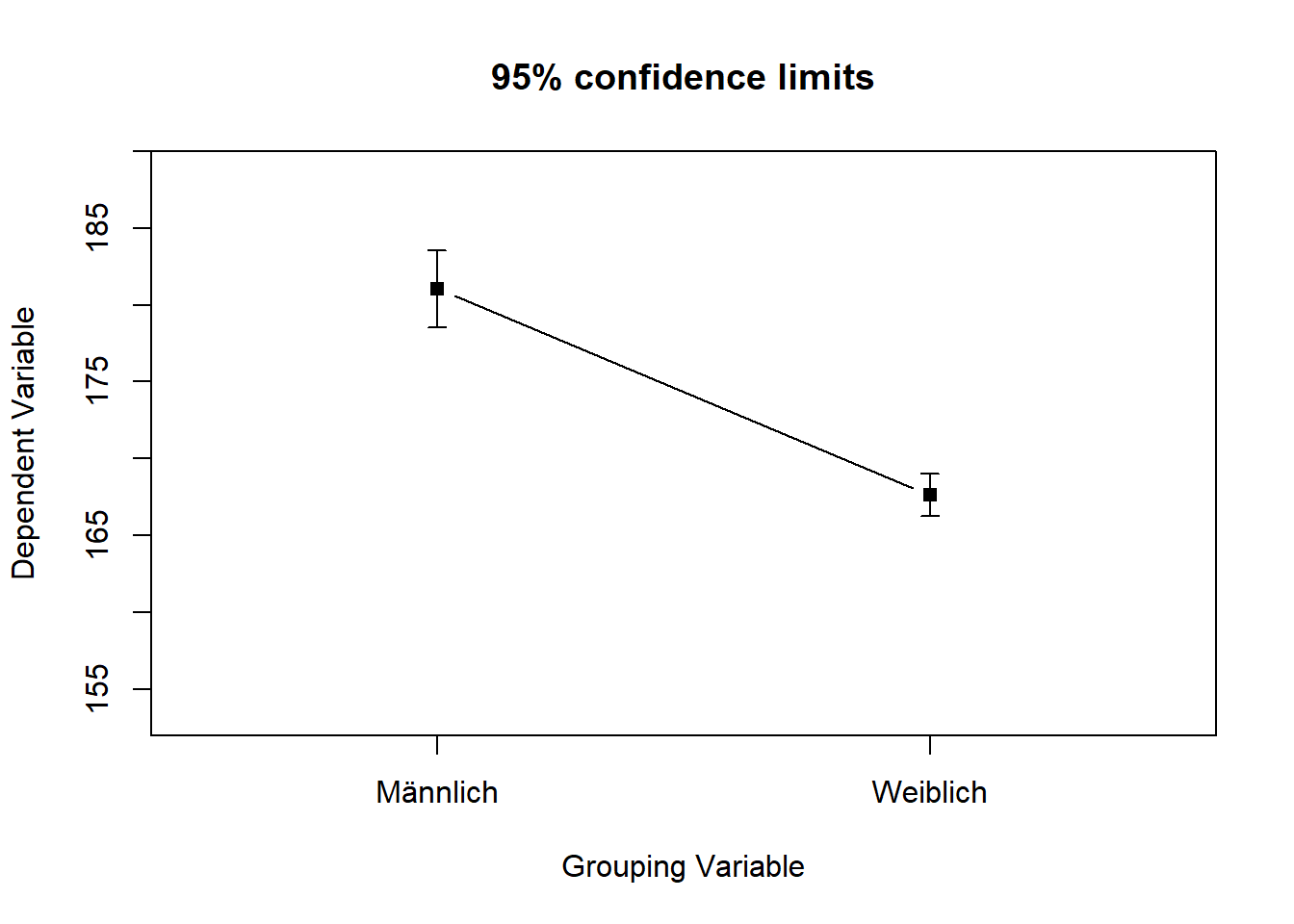
Wenn sich die Konfidenzintervalle für zwei Mittelwerte nicht überschneiden, wie in diesem Beispiel, bedeutet dies, dass der Unterschied zwischen den beiden Mittelwerten statistisch signifikant ist. Ein Konfidenzintervall stellt den Wertebereich dar, in dem der wahre Mittelwert auf der Grundlage eines bestimmten Konfidenzniveaus (in der Regel 95 %) wahrscheinlich liegen wird. Wenn sich die Konfidenzintervalle für zwei Mittelwerte nicht überschneiden, bedeutet dies, dass die wahren Mittelwerte für die beiden Gruppen wahrscheinlich unterschiedlich sind.
Machen wir ein weiteres Beispiel aus dem Datensatz WPStudis. Wer ist zufriedener in der Beziehung, Männer oder Frauen?
error.bars.by(WPStudis$F21_03_Zufriedenheit_Partnerschaft,WPStudis$F3_Geschlecht,eyes=FALSE, v.labels=cbind("Männlich","Weiblich"))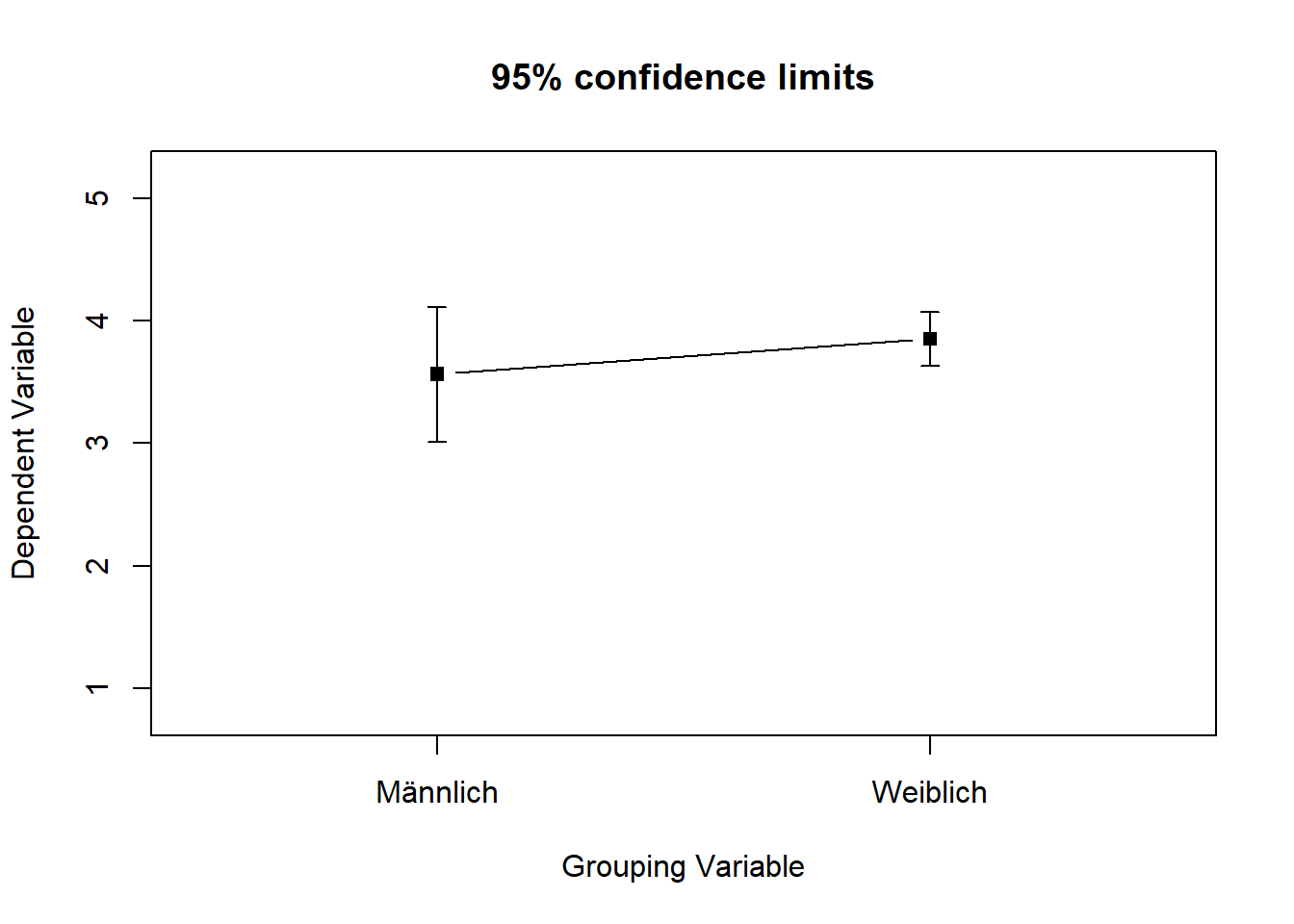
Deskriptiv ist der Wert der Frauen höher, aber wie man sieht überschneiden sich die Konfidenzintervalle nicht. Der Unterschied der Mittelwerte ist also nicht signifikant und wir können daher nicht sagen, dass Frauen auch in der Population zufriedener sind als Männer.
In diesem Video zeige ich, wie das in R funktioniert:
Histogramm
Ein Histogramm ist eine grafische Darstellung der Verteilung eines Datensatzes. Ein Histogramm sieht auf den ersten Blick aus wie ein Säulendiagramm, ist aber dennoch eine andere Darstellungsform. Ein Histogramm wird verwendet, um die Verteilung von kontinuierlichen Daten, wie Messwerten oder Zeitdaten, darzustellen. Die x-Achse eines Histogramms stellt die Werte im Datensatz dar, die y-Achse die Häufigkeit, d. h. die Anzahl, mit der dieser Wert im Datensatz erscheint. Die Balken in einem Histogramm liegen in der Regel ohne Zwischenraum nebeneinander und haben in der Regel die gleiche Breite.
Ein Balkendiagramm hingegen wird verwendet, um die Werte verschiedener Kategorien oder Gruppen zu vergleichen. Die x-Achse eines Balkendiagramms steht für die Kategorien oder Gruppen, die y-Achse für die Werte. Kategorien, die in den Daten nicht vorkommen, werden nicht angezeigt. In einem Histogramm hingegen, werden diese als “Lücken” sichtbar. Daher ist ein Histogramm besonders dazu geeignet, die Verteilungsform zu interpretieren.
Ein Histogramm kann direkt mit hist() erstellt werden. Hier ein Beispiel aus unserem Datensatz:
hist(WPStudis$F4_Koerpergroesse)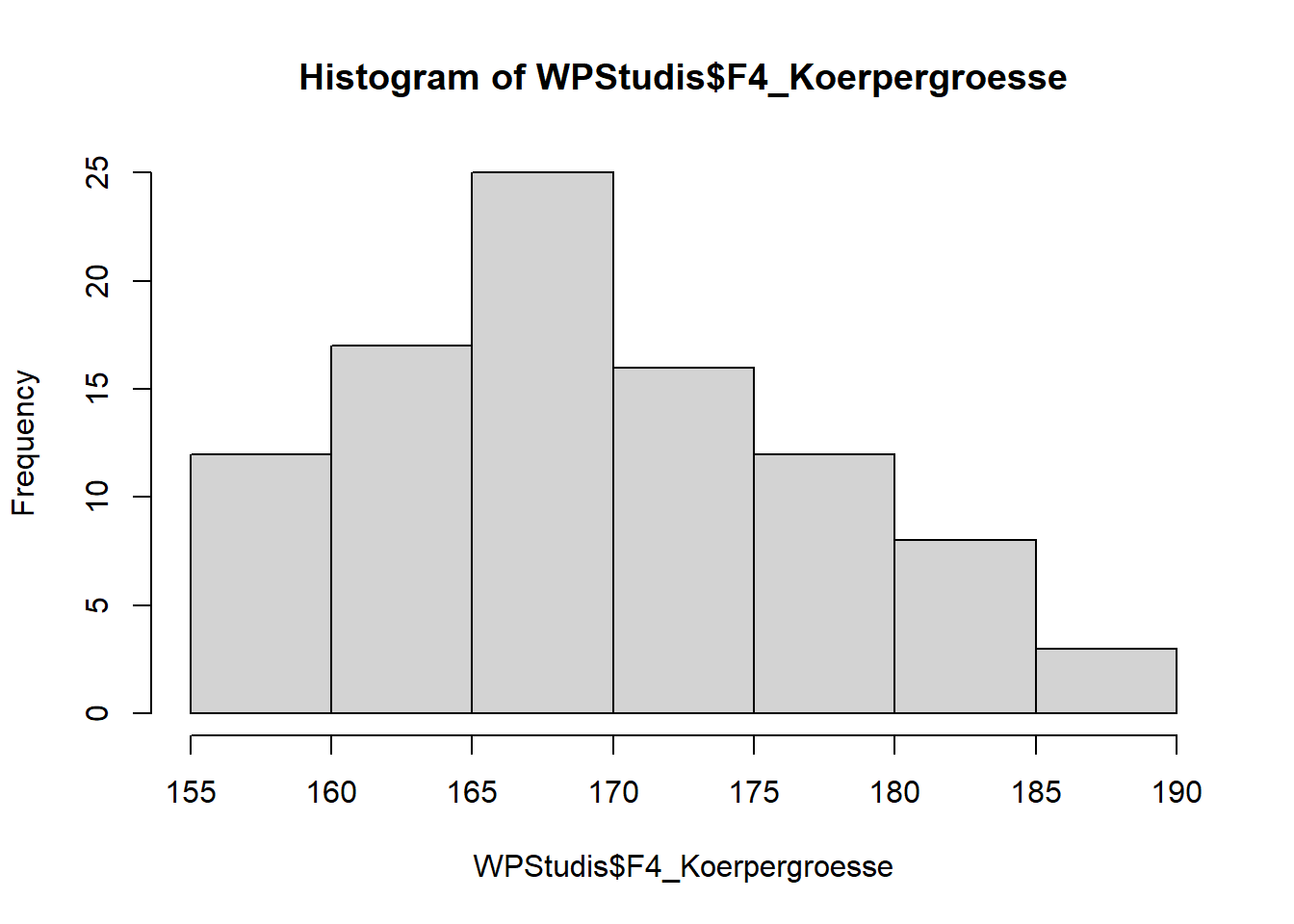
Versuchen wir mal schrittweise diese Grafik zu “verschönern”
In einem Histogramm können wir die Anzahl der Säulen selbst bestimmen. Hierzu nutzen wir das Argument breaks. Wenn wir die Balkenzahl in unserem Beispiel erhöhen wollen, könnten wir also wie folgt vorgehen. Spielen Sie doch mal mit diesem Wert und betrachten Sie, wie sich die Verteilungsform verändert.
hist(WPStudis$F4_Koerpergroesse, breaks=30)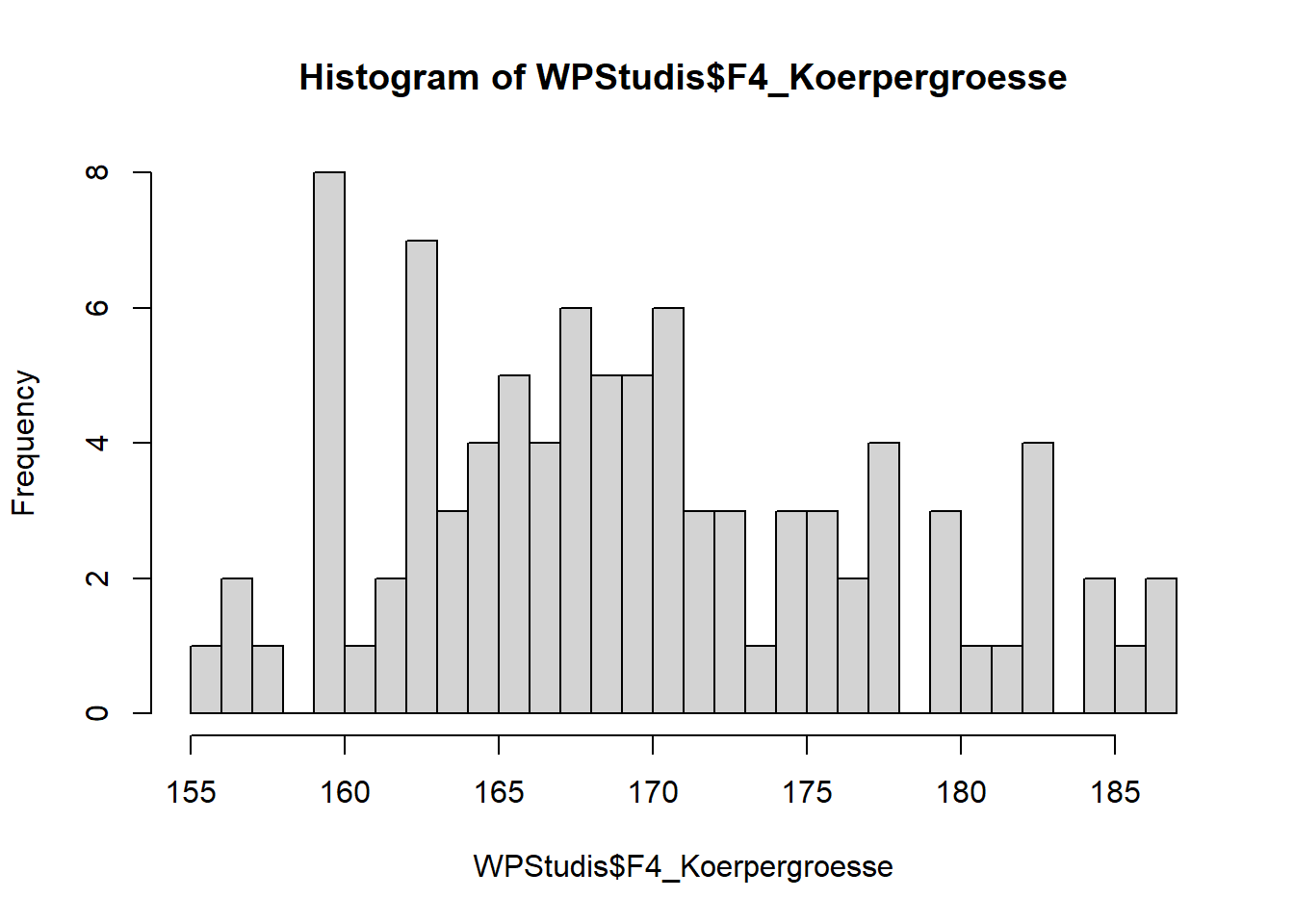
Wir können natürlich auch hier wieder einen Titel einfügen, die Achsen vergrößern und benennen, die Farben ändern etc. Hier ein weiteres Beispiel:
hist(WPStudis$F4_Koerpergroesse, breaks=15,
main="Histogramm Körpergroesse",
xlim=c(150,190), ylim=c(0,12),
xlab="groesse WP-Studierende",
ylab="Häufigkeit",
col="tomato",
border="white")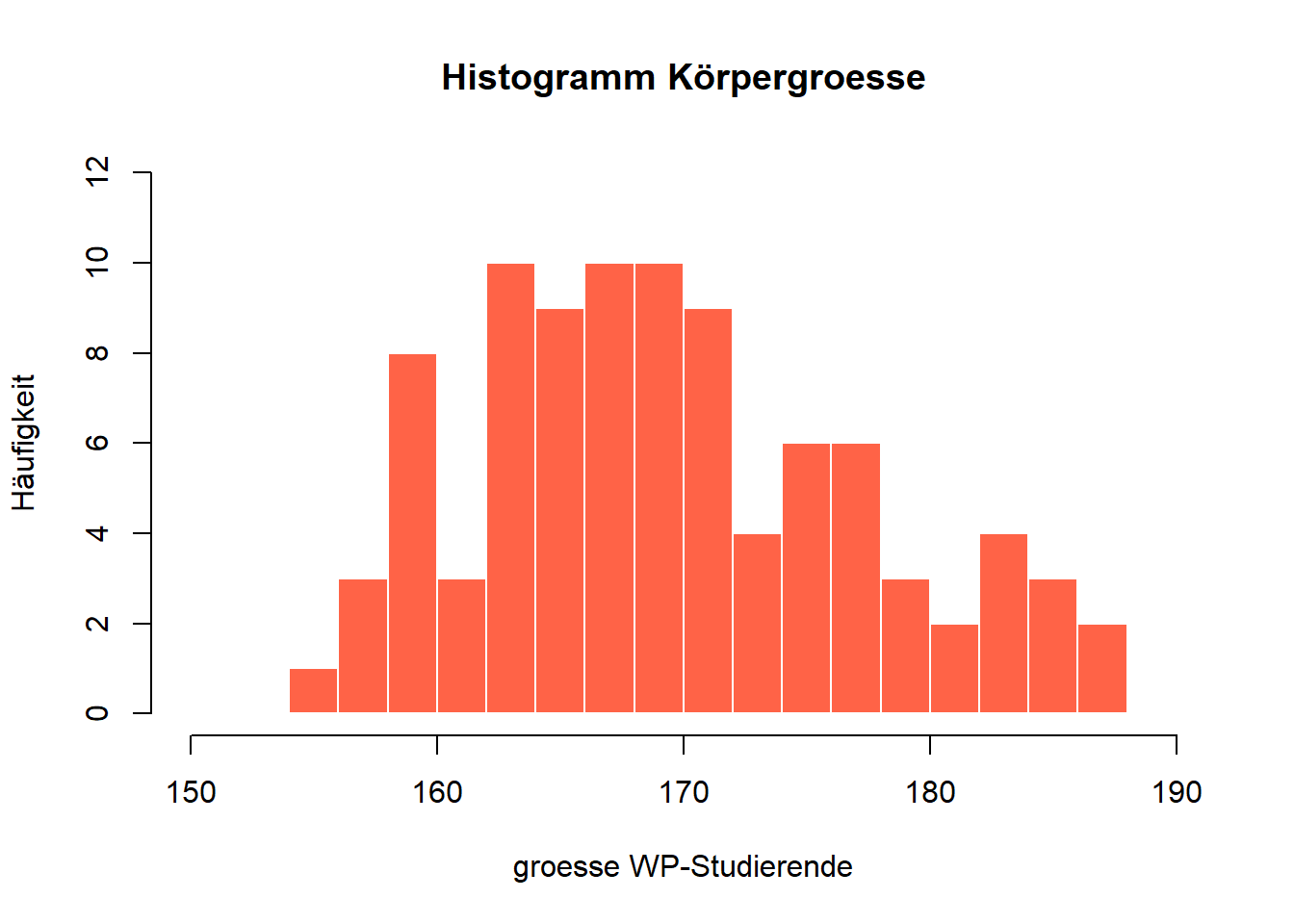
Statt die Anzahl der Balken zu definieren, kann man auch ein sog. Kerndichte-Diagramm erstellen. Hierbei werden die Häufigkeiten nicht als Balken, sondern als durchgezogene Linie dargestellt (Dies entspricht dem Gedankenexperiment von unendlich vielen Balken).
plot(density(WPStudis$F4_Koerpergroesse))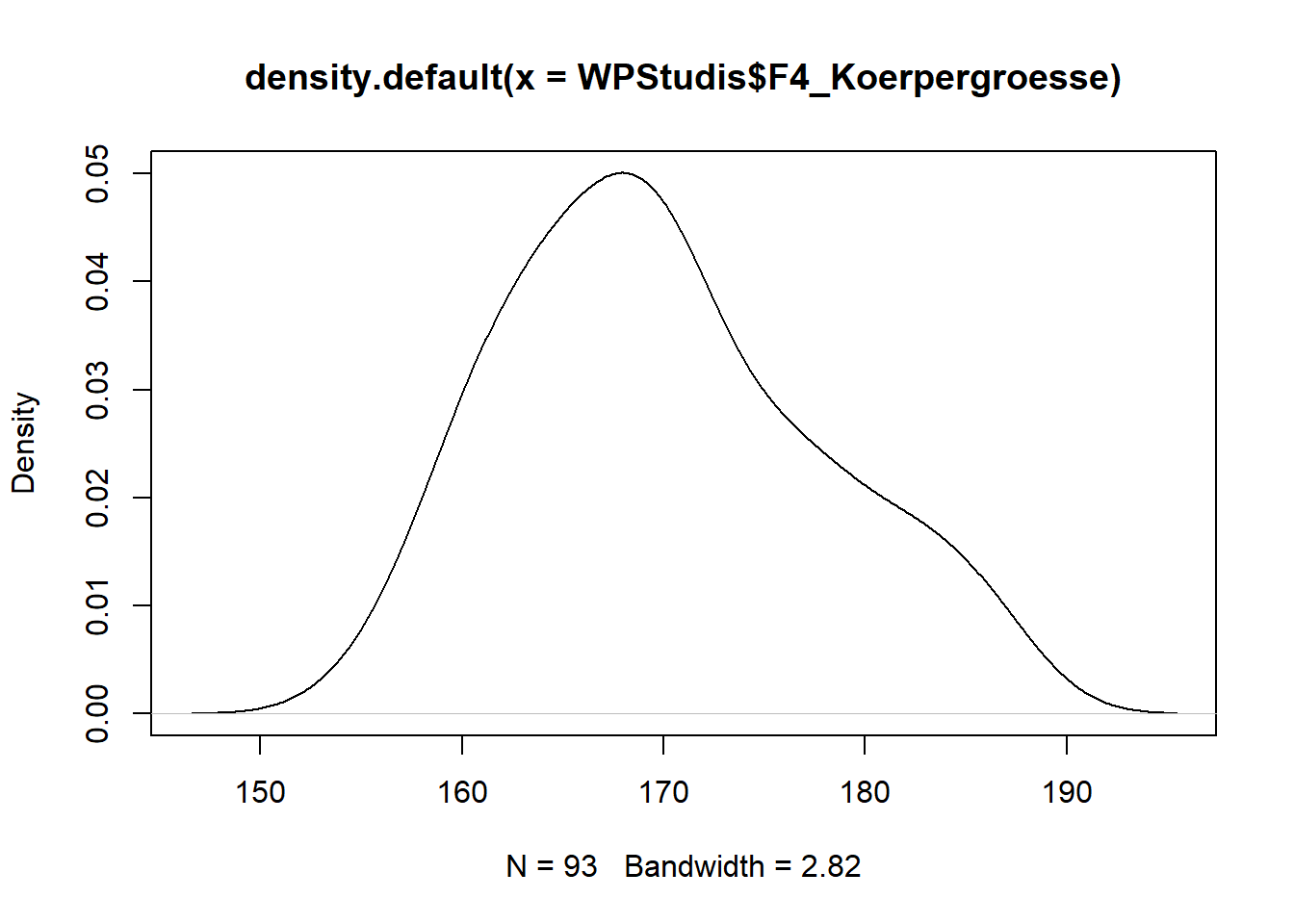
In diesem Video zeige ich, wie das in R funktioniert:
Übung
Entwerfen Sie ein Histogramm für die Anzahl der Freunde auf Facebook der WP Studierenden mit 10 Klassen (Balken).
Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.
Boxplot
Ein Boxplot, auch bekannt als Box-and-Whisker-Plot, ist eine grafische Darstellung der Verteilung eines Datensatzes. Er wird verwendet, um die Streuung eines Datensatzes sowie Ausreißer oder ungewöhnliche Werte darzustellen. Der Boxplot besteht aus einer Reihe von verschiedenen Komponenten:
- Die Box: Diese stellt den Interquartilsbereich (IQR) des Datensatzes dar, d. h. den Bereich der mittleren 50 % der Daten.
- Die Whisker: Diese erstrecken sich auf beiden Seiten der Box bis zu den Minimal- und Maximalwerten des Datensatzes, wobei Ausreißer ausgeschlossen werden.
- Die Linie innerhalb der Box: Dies ist der Median (Mittelwert) des Datensatzes.
- Die Punkte: Sie stellen die Ausreißer dar, d. h. die Werte, die außerhalb der Whiskers liegen. Diese erhalten in R eine Ziffer, die die Zeilennummer im Datensatz darstellt.
Boxplots sind besonders nützlich, um die Verteilung mehrerer Datensätze zu vergleichen (Histogramme können die Verteilungsform von nur einer Variablen darstellen).
Ein Boxplot kann direkt mit boxplot() erstellt werden. Aus unserem Datensatz:
boxplot(WPStudis$F2_Alter)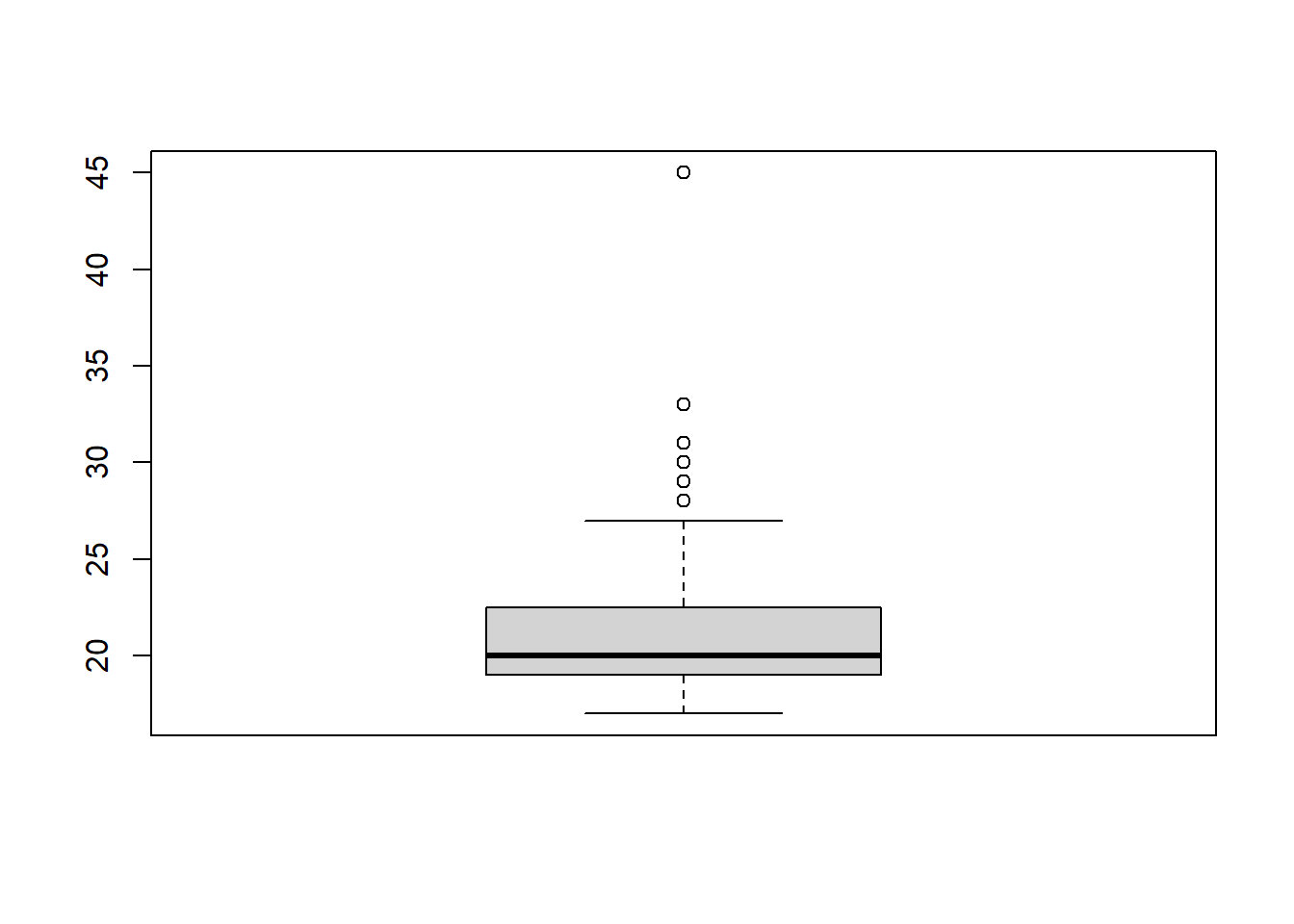
Auch Gruppierungen lassen sich leicht erzeugen. Hierzu nutzen wir wieder das Format: Variable1 ~ Variable2. Hier ein Beispiel:
boxplot(WPStudis$F4_Koerpergroesse~WPStudis$F3_Geschlecht)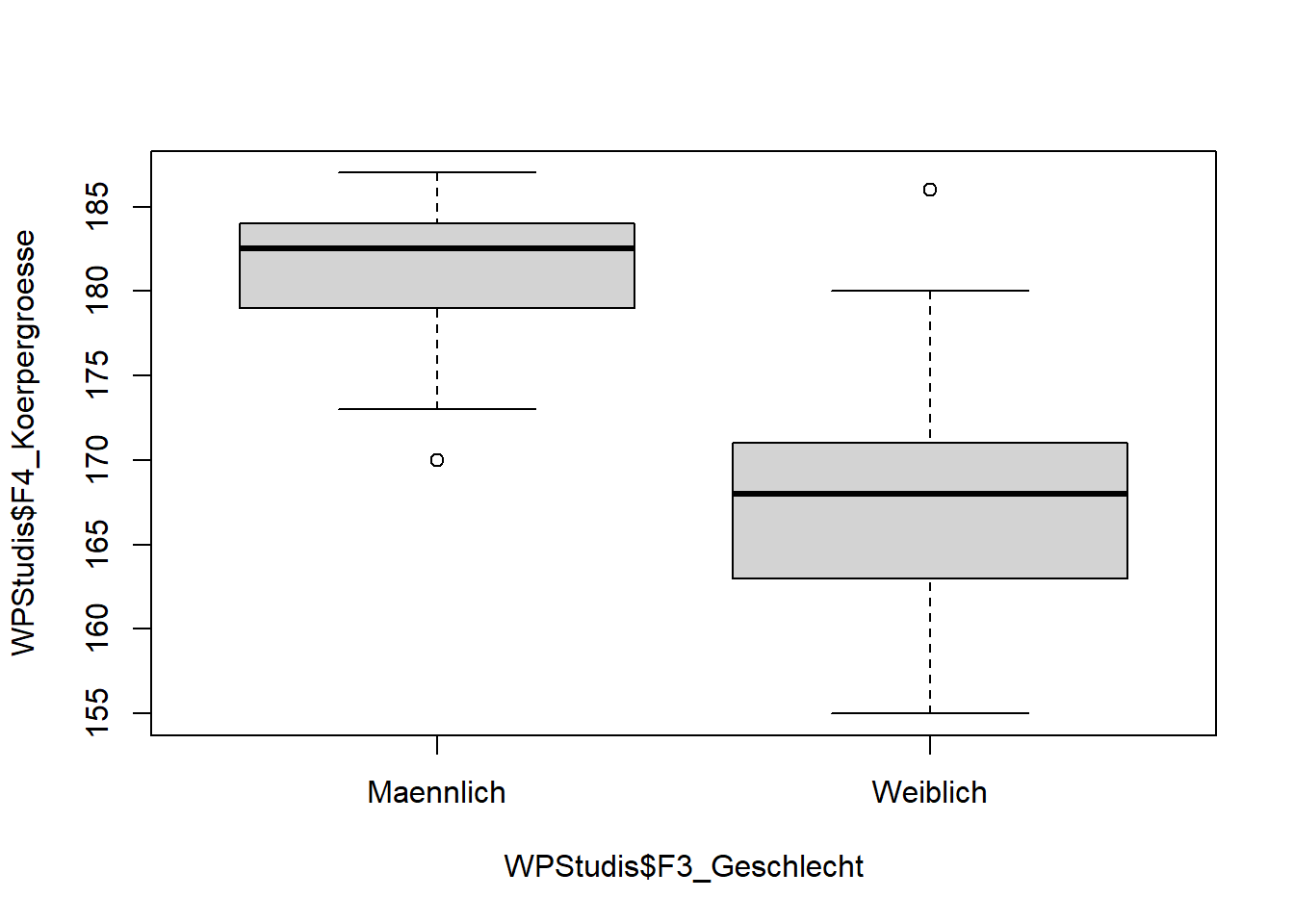
Wir können auch hier die Farben ändern und Beschriftungen vornehmen. Hierzu müssen wir hier jedoch das names Argument verwenden.
boxplot(WPStudis$F4_Koerpergroesse~WPStudis$F3_Geschlecht,
col=("darkgreen"),
names=c("Männlich","Weiblich"))
In diesem Video zeige ich, wie das in R funktioniert:
Übung
Entwerfen Sie zwei Boxplots nebeneinander für die Schuhgroesse der weiblichen bzw. männlichen Studierenden.
Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.
Kreisdiagramm
Ein Kreisdiagramm ist eine kreisförmige grafische Darstellung von Daten, wobei der gesamte Kreis den Gesamtwert der Daten darstellt und jedes Segment oder “Stück” des Kuchens eine andere Kategorie oder Gruppe repräsentiert. Die Größe jedes Segments ist proportional zu der Menge oder dem Prozentsatz der Daten, die es repräsentiert.
Tortendiagramme sind besonders nützlich, wenn die Daten eine geringe Anzahl verschiedener Kategorien aufweisen und wenn die relative Größe der Kategorien wichtiger ist als ihre genauen Werte. Es kann jedoch schwierig sein, die Größe kleiner Scheiben zu vergleichen, insbesondere wenn es viele davon gibt. Da Tortendiagramme zur Darstellung von Daten Winkel und nicht Längen verwenden, kann es außerdem schwierig sein, die Größe der Scheiben genau zu vergleichen.
Hier ein Beispiel aus unserem Datensatz:
pie(table(WPStudis$F7_Brille)) 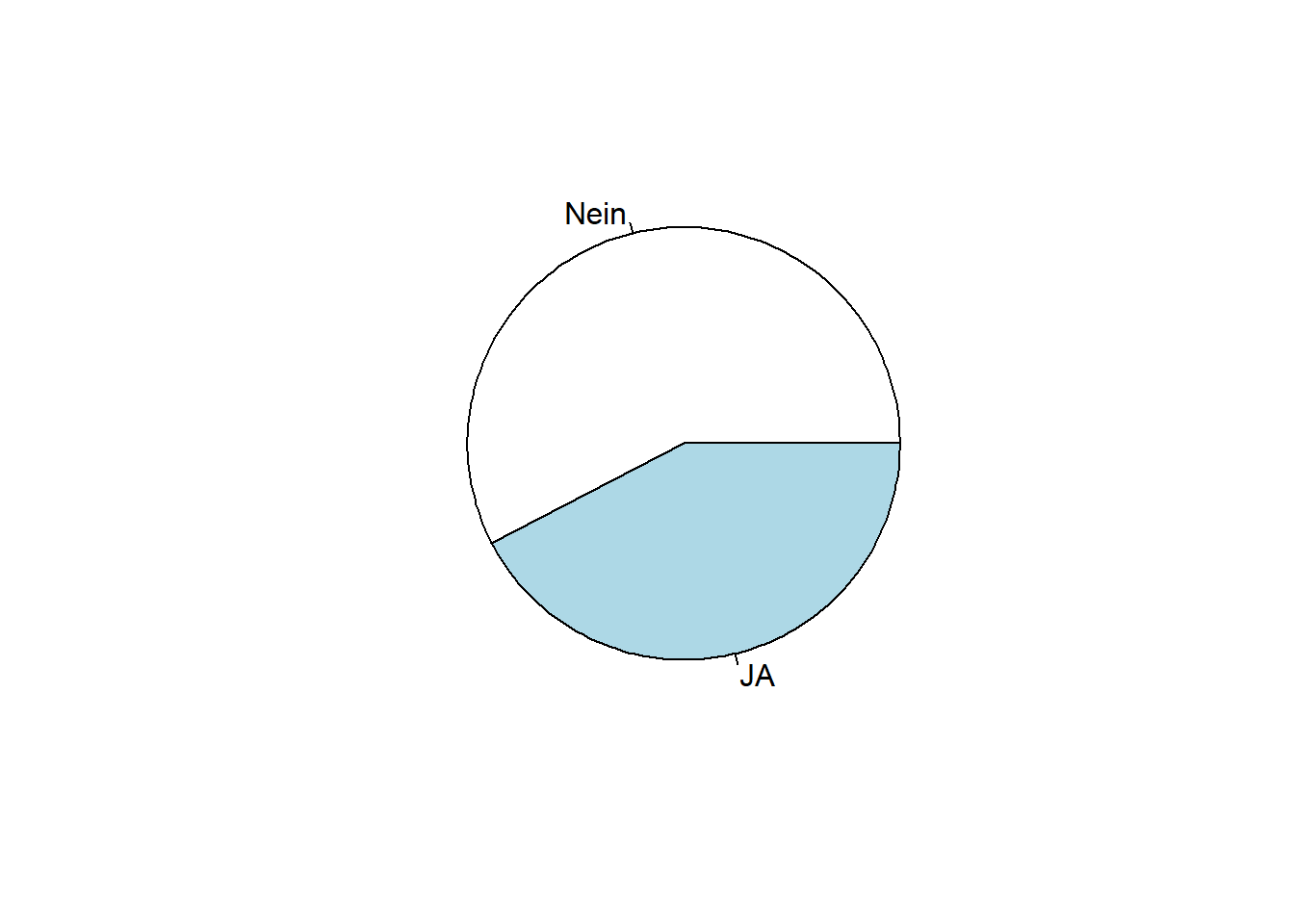
Um den Startpunkt auf “12 Uhr” zu stellen, kann zusätzlich das Argument clockwise=T verwendet werden
pie(table(WPStudis$F7_Brille), clockwise=T) 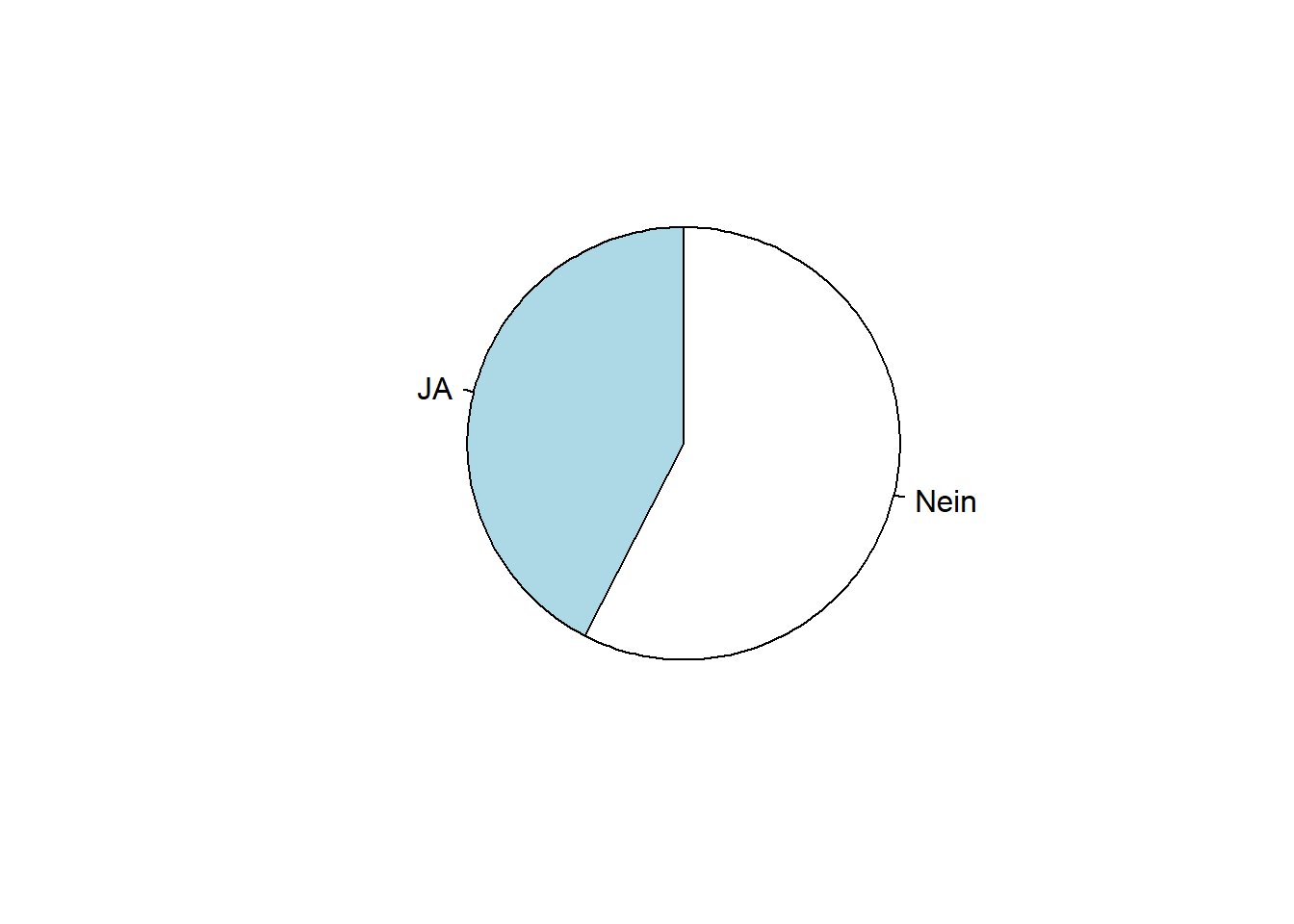
In diesem Video zeige ich, wie das in R funktioniert:
Übung
Erzeugen Sie ein Kreisdiagramm für das Geschlecht unserer Ersties (Datensatz WPStudis)
Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.
Streudiagramm
Ein Streudiagramm ist eine grafische Darstellung von zweidimensionalen Daten, bei der jeder Punkt im Diagramm ein Wertepaar aus einem Datensatz darstellt. Die x-Achse steht für eine Variable und die y-Achse für die andere Variable. Die Position jedes Punktes im Diagramm entspricht den Werten der beiden Variablen für diesen Punkt. Streudiagramme werden verwendet, um die Beziehung zwischen zwei Variablen zu visualisieren und um Muster oder Trends in den Daten zu erkennen.
Streudiagramme sind nützlich, um Muster und Trends in den Daten zu erkennen, z. B. lineare Beziehungen, nicht lineare Beziehungen, Cluster und Ausreißer. Auch die Verteilung der Daten und die Streuung der Werte lassen sich damit visualisieren. Streudiagramme sind besonders nützlich für große Datensätze, da sie eine große Anzahl von Datenpunkten in einem einzigen Diagramm darstellen können.
Das Generieren von Streudiagrammen in R haben wir schon kennengelernt, diese lassen sich mit der plot() Funktion sehr einfach generieren.
plot(WPStudis$F4_Koerpergroesse~WPStudis$F5_Schuhgroesse)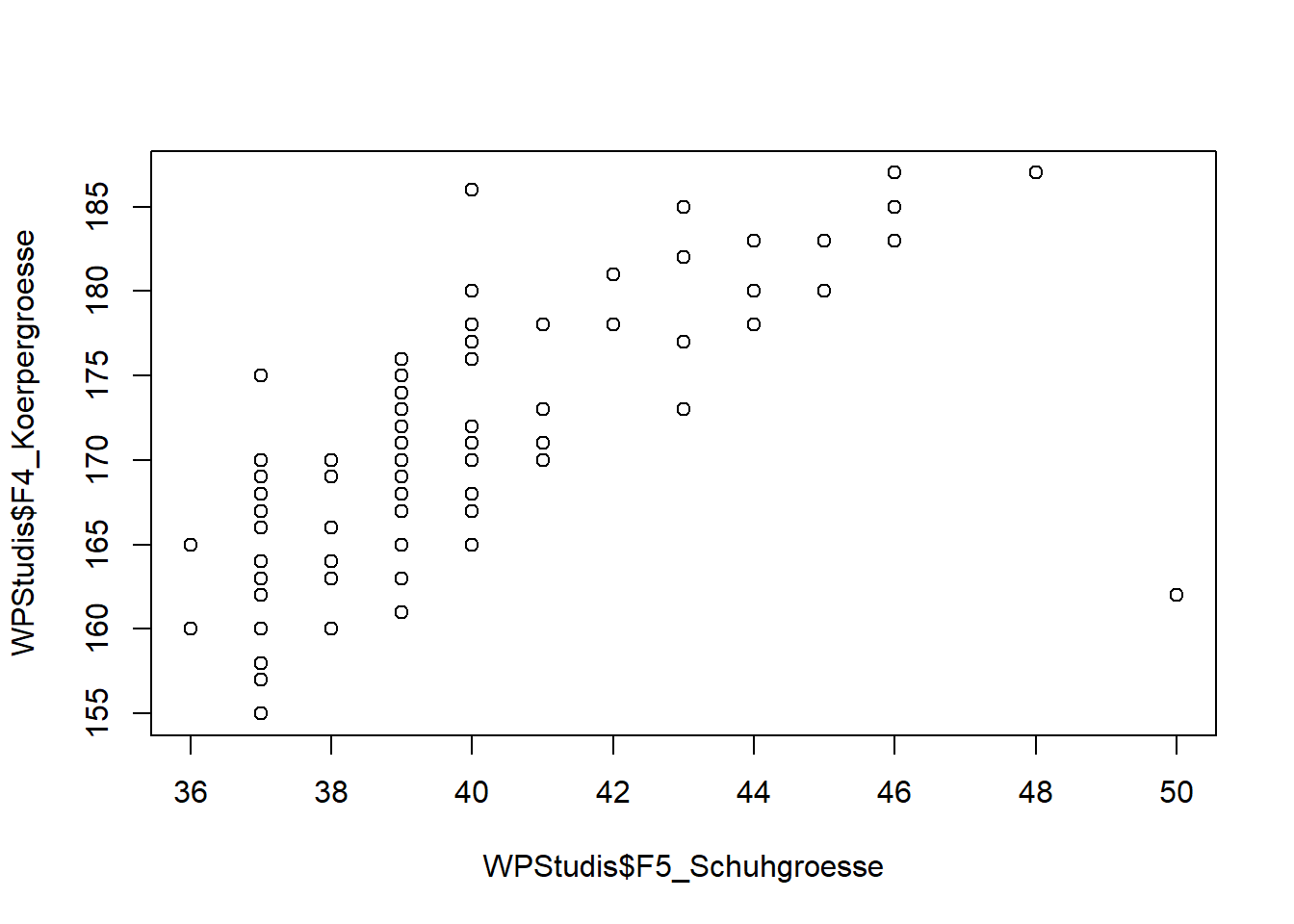
Eine Regressionsgerade können wir durch den Befehl abline sowie durch die Spezifikation des linearen Modells (lm) hinzufügen. Den Aufbau des linearen Modells und das Thema Regression besprechen wir noch in den folgenden Kapiteln. Grundsätzlich gilt, dass in der lm() Funktion zunächst die abhängige Variable, die auf der y-Achse abgetragen wird und dann die unabhängige Variable, die auf der x-Achse abgetragen wird, getrennt wird von einer Tilde (~).
plot(WPStudis$F4_Koerpergroesse~WPStudis$F5_Schuhgroesse)
abline(lm(WPStudis$F4_Koerpergroesse~WPStudis$F5_Schuhgroesse))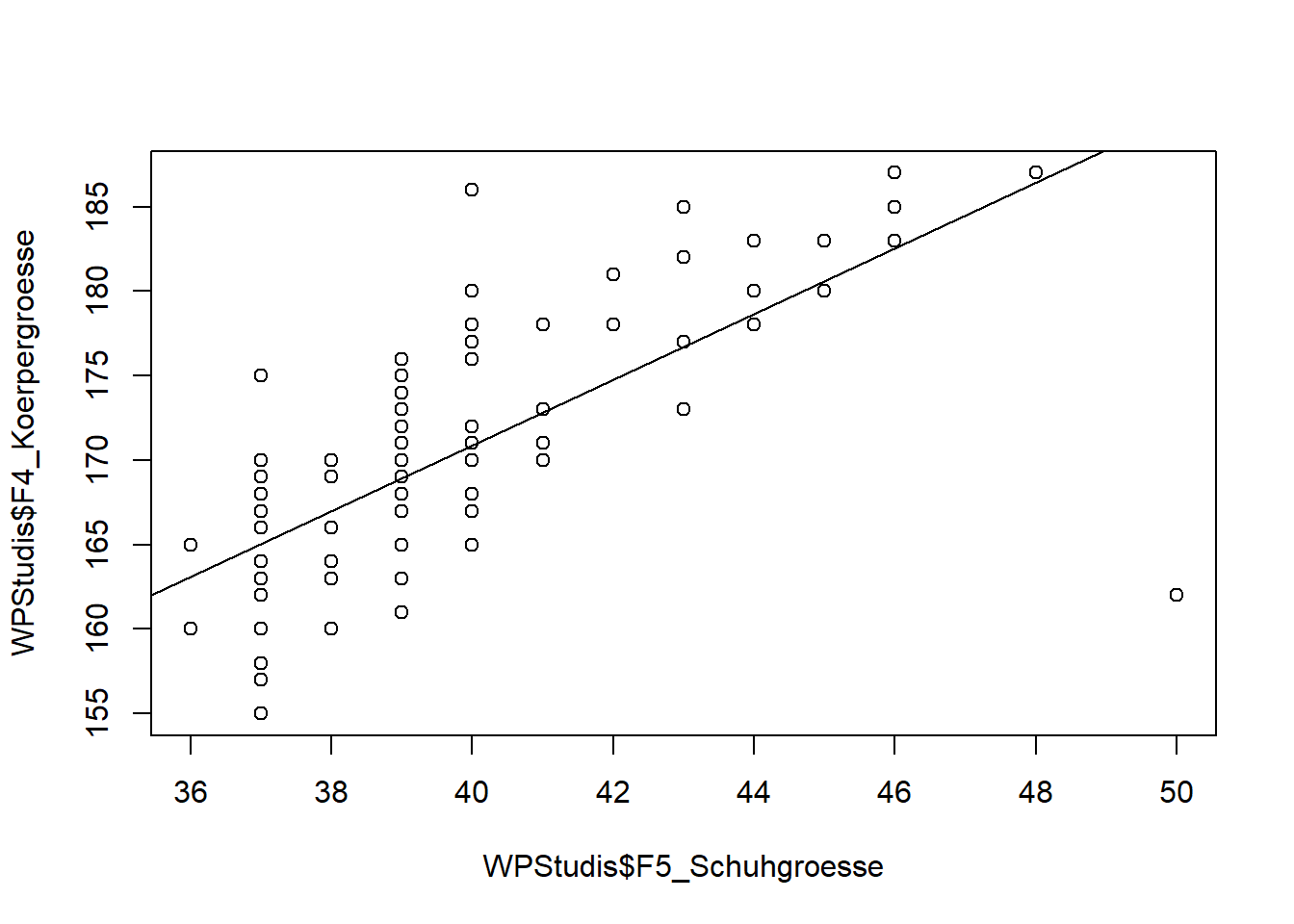
Streudiagramm-Matrizen
R kann auch sogenannte Streudiagramm-Matrizen erstellen, die übersichtlich den Zusammenhang von mehr als 2 Variablen darstellen. Hierfür benötigen wir die Funktion pairs.panels() aus dem psych Paket.
Die Funktion pairs.panels() erstellt eine Matrix von Streudiagrammen, in der jede Variable gegen jede andere Variable aufgetragen wird. Sie kann verwendet werden, um die Beziehungen zwischen mehreren Variablen zu visualisieren und um Muster oder Trends in den Daten zu erkennen. Die Funktion verfügt über mehrere Optionen, mit denen Sie das Aussehen des Diagramms anpassen können, z. B. die Größe der Punkte, die Farbe der Punkte und die Art der zu verwendenden Glättung.
Als Input benötigen wir hier jedoch einen Data-Frame. Diesen können wir vorab generieren oder direkt in die Funktion einbauen, mithilfe der data.frame Funktion.
Im folgenden Beispiel erstellen wir einen Data-Frame mit den gewünschten drei Variablen. Diese müssen alle als Vektoren formatiert sein.
Zusammenhang <- data.frame(WPStudis$F4_Koerpergroesse, WPStudis$F5_Schuhgroesse, WPStudis$F20_Einkommen_Glueck)Nun können wir die Funktion auf unseren neuen Datensatz anwenden.
pairs.panels(Zusammenhang)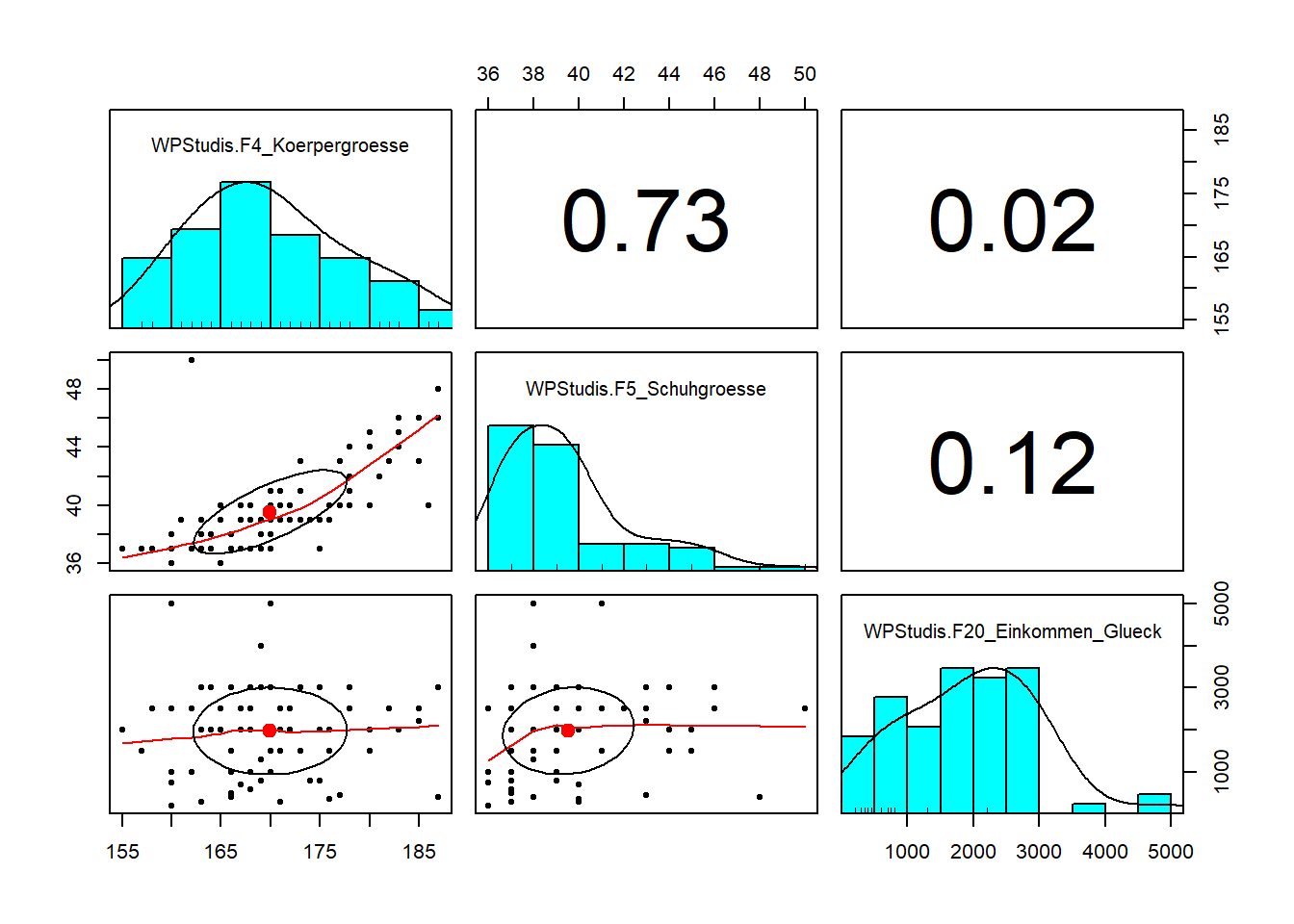
Wenn man die Funktion auf unseren ganzen Datensatz anwendet, wird es jedoch unübersichtlich.
pairs.panels(WPStudis)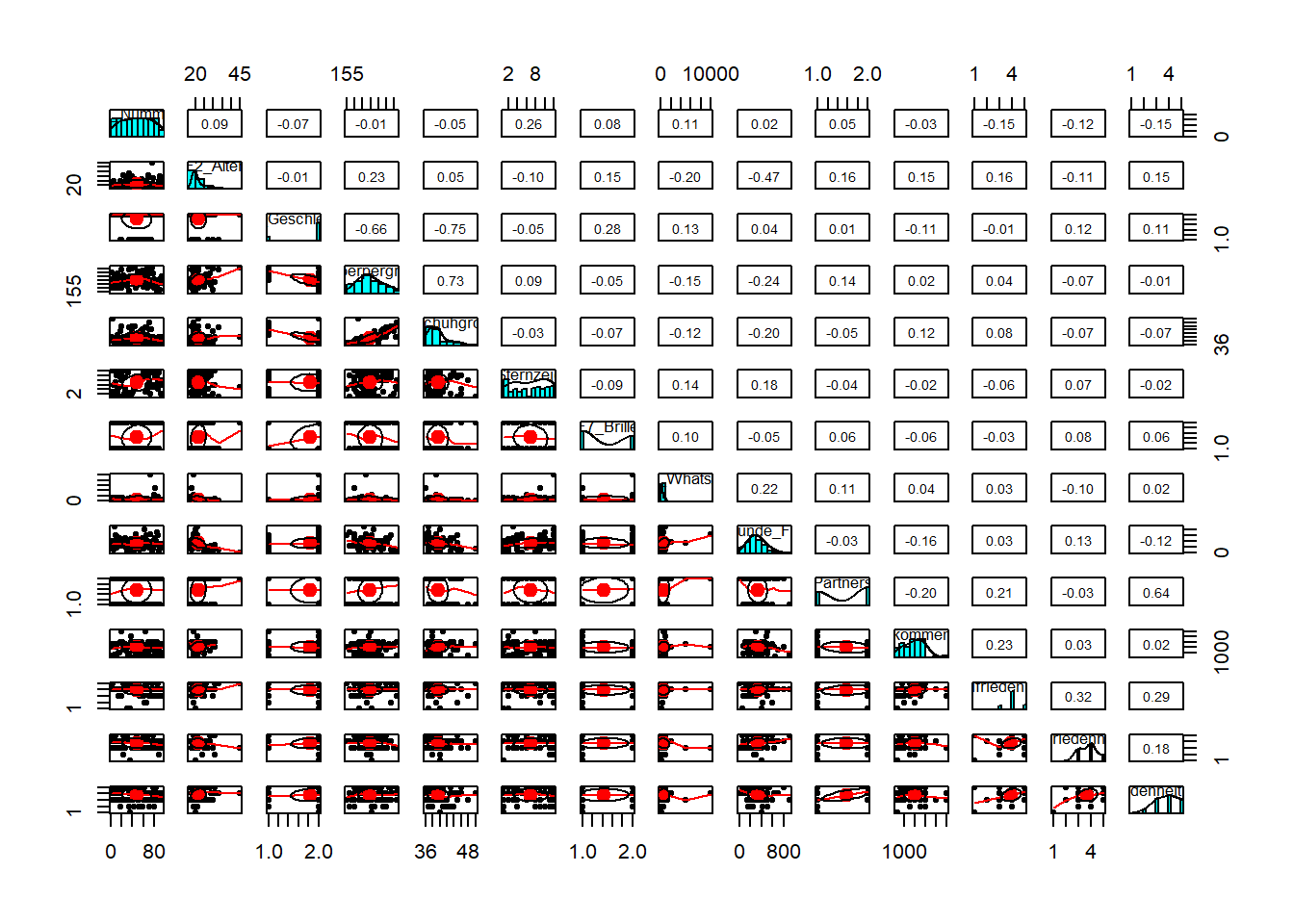
Alternativ gibt es weitere Pakete mit denen Streudiagramm-Matrizen erstellt werden könnnen. Insbesondere wenn viele Variablen betrachtet werden sollen, ist z. B. corrgram eine gute Alternative. Die Funktion erstellt eine Matrix von Zellen, wobei jede Zelle den Korrelationskoeffizienten zwischen zwei verschiedenen Variablen darstellt. Die Zellen sind farbkodiert, um die Stärke und Richtung der Korrelation anzuzeigen. Blaue Farben zeigen positive, rote Farben negative Korrelationen. Je stärker die Korrelation, desto dunkler die Farbe. Hier ein Beispiel:
Beispiel corrgramm
library("corrgram")
corrgram(WPStudis)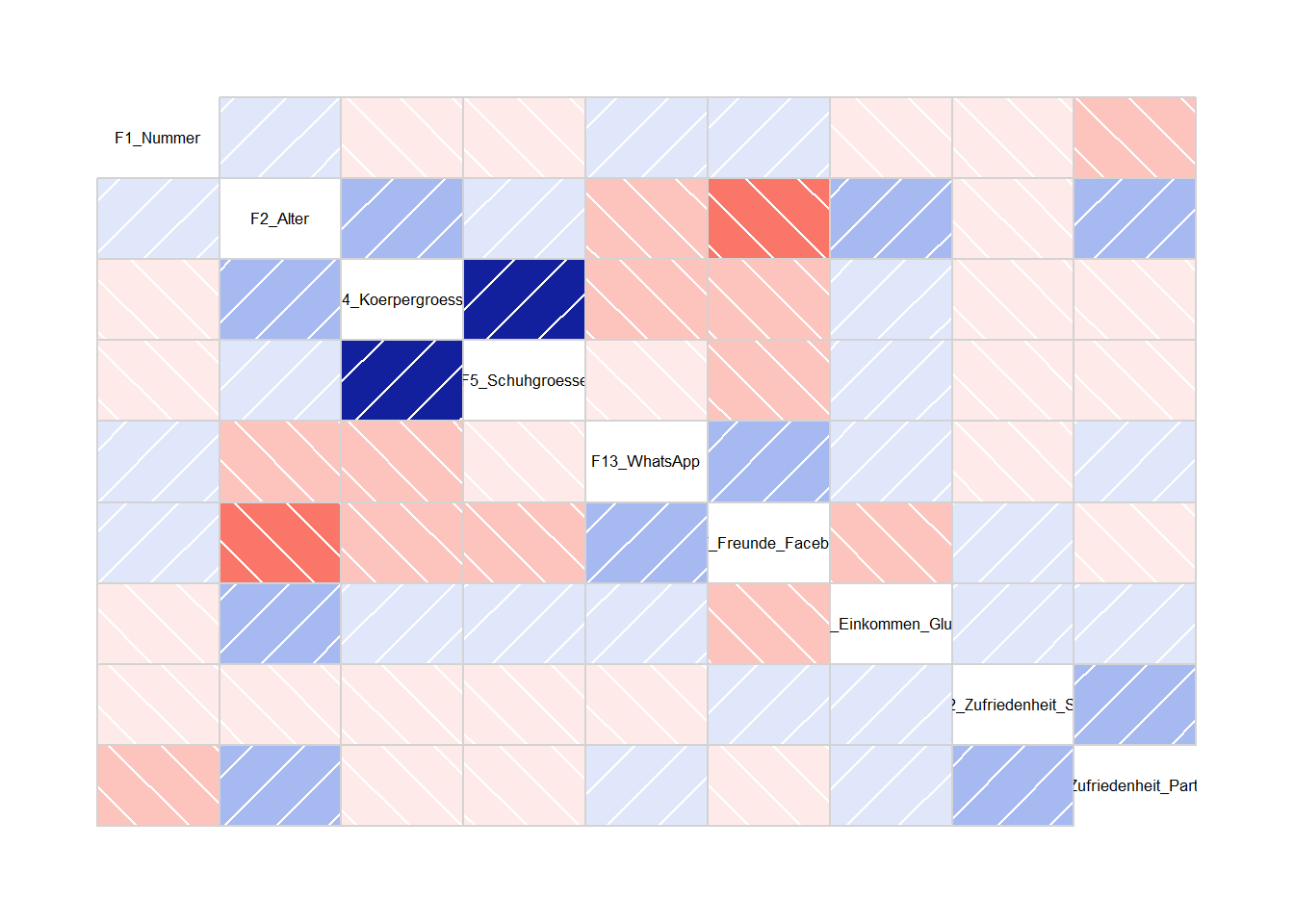
Alternativ kann mit der Funktion corrgram auch eine Hälfte der Kombinationon mit Piecharts dargestellt werden. Dadurch kann die Stärke der Korrelation noch exakter abgelesen werden.
corrgram(WPStudis, upper.panel=panel.pie)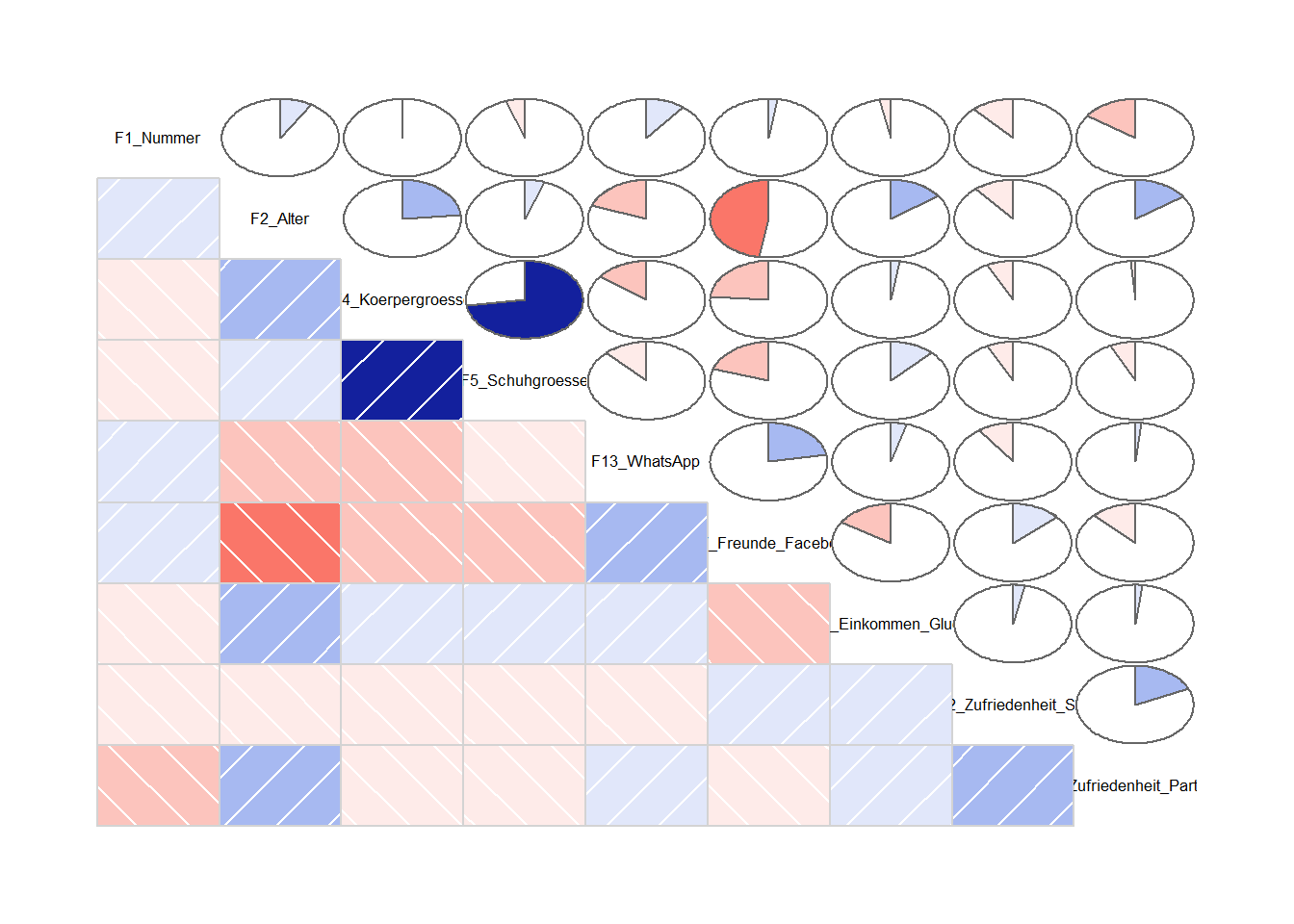
In diesem Video zeige ich, wie das in R funktioniert:
Übung
Wir haben echte Daten der Besucherfrequenz in der Fussgängerzone von Stuttgart.
Um die Daten aus Excel zu laden, nutzen wir das readxl Paket und die read_excel Funktion.
Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.
library(readxl)
Passanten <- read_excel("Passanten2019.xlsx")Wir müssen zunächst die Variable “Tag” in einen Faktor umwandeln. Damit die Tage dann noch in unserer gewohnten Reihenfolge erscheinen (Mo-So), können Sie einen ordered Factor erstellen. Dies geht wie folgt:
Passanten$Tag <- as.factor(Passanten$Tag)
Passanten$Tag <- ordered(Passanten$Tag,levels=c("Mo","Di","Mi","Do","Fr","Sa","So"))Versuchen Sie Boxplots zu erzeugen, die uns sagen, an welchem Wochentag wieviele Menschen auf der Königstrasse unterwegs sind.
Versuchen Sie zusätzlich Boxplots zu erzeugen, die die Standorte Königstrasse Mitte und Süd vergleichen.
Übung
Wir laden die Daten (Befragung von Paaren nach der Aufteilung der Hausarbeit, aufgeteilt in 13 klassische Hausarbeiten) aus dem Paket ade4.
library(ade4)
data(housetasks)Betrachten Sie die Daten. Erzeugen Sie eine Grafik, um die Daten möglichst gut zu visualisieren.
Tipp: Sie benötigen zunächst eine Tabelle mit den relativen Häufigkeiten. Um diese besser darstellen zu können, lohnt es sich zudem, die Tabelle zu transponieren (Die Spalten und Zeilen zu tauschen). Hierzu können Sie die t() Funktion in R nutzen.
data<-as.matrix(housetasks) #Erzeugt eine Daten-Matrix (Voraussetzung für viele Plots bzw. die Umwandlung in eine Tabelle)
data<-100*prop.table(data, margin = 1) #Erzeugt eine Kontinenztabelle mit Zeilenprozenten
data_trans <-t(data) #Die Funktion t() erzeugt eine transponierte Matrix (X und Y Achse getauscht)
Grafiken mit GGPlot2
Das Paket ggplot2 ist der Goldstandard für Grafiken in R, aber auch eine eigene Programmiersprache innerhalb von R, die man sich aneignen muss. Es ist das beliebteste Datenvisualisierungspaket in R, das einen leistungsstarken und flexiblen Rahmen für die Erstellung verschiedener Arten von Diagrammen bietet. Es gibt mehrere Gründe, warum Nutzer ggplot2 gegenüber anderen Visualisierungspaketen oder -methoden bevorzugen:
- Grammatik der Grafik: ggplot2 basiert auf der “Grammatik der Grafik”, die eine konsistente und flexible Methode zur Erstellung von Plots bietet. So können Sie Ihre Plots leicht anpassen und modifizieren und komplexe Plots durch die Kombination mehrerer Ebenen erstellen.
- Eingebaute Unterstützung für mehrere Skalen: ggplot2 hat eingebaute Unterstützung für verschiedene Skalen, wie z. B. kontinuierliche, kategoriale und Datumsskalen, was die Erstellung von Plots für verschiedene Datentypen erleichtert.
- Anpassbare Themen: ggplot2 bietet eine Reihe von eingebauten Themen, mit denen Sie das Aussehen Ihrer Diagramme schnell ändern können. Sie können auch Ihre eigenen Themen erstellen, um den Stil Ihrer Organisation oder Ihres Projekts anzupassen.
- Viele Geoms: ggplot2 unterstützt viele Arten von Geoms (geometrische Objekte bzw. Darstellungsarten), mit denen verschiedene Arten von Diagrammen erstellt werden können, wie z. B. Streudiagramme, Liniendiagramme, Balkendiagramme und viele mehr. Es unterstützt auch eine Vielzahl von statistischen Transformationen, die zur Visualisierung und Analyse von Daten verwendet werden können.
Vorbereitung
Datensatz ‘WPStudis.RData’ öffnen (Sie muessen ggf. noch Ihren Pfad ändern bzw. den Workspace neu definieren):
load("WPStudis.Rdata")Paket aktivieren
library(ggplot2)QPlot und GGPlot
Qplot ist so konzipiert, dass es einfacher und bequemer zu benutzen ist als ggplot(), um gängige Arten von Diagrammen zu erstellen, wie z. B. Streudiagramme, Balkendiagramme und Histogramme. Gleichzeitig hat es deutlich weniger Optionen und Argumente. Wenn es schnell gehen muss, kann qplot() dennoch eine Alternative sein. Hier ein Beispiel:
qplot(data=WPStudis,x=F6_Sternzeichen,y=F5_Schuhgroesse,color=F3_Geschlecht)
## Warning: `qplot()` was deprecated in ggplot2 3.4.0.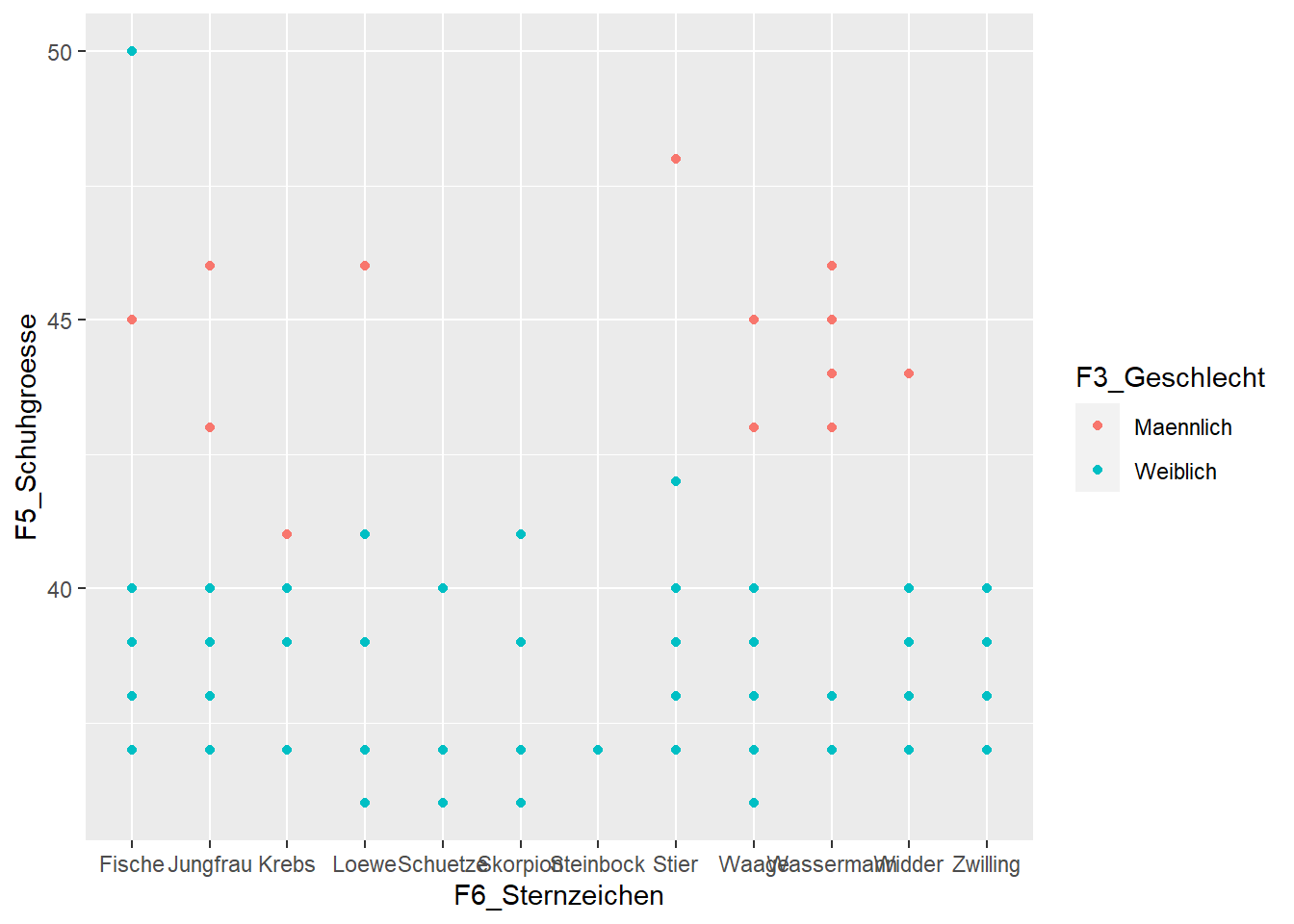
Die gleiche Grafik mit ggplot() braucht deutlich mehr Argumente, ist dafür aber auch beliebig erweiterbar. Wie das geht, schauen wir uns im nächsten Schritt an.
ggplot() + geom_point(data=WPStudis,aes(x=F6_Sternzeichen,y=F5_Schuhgroesse,colour=F3_Geschlecht))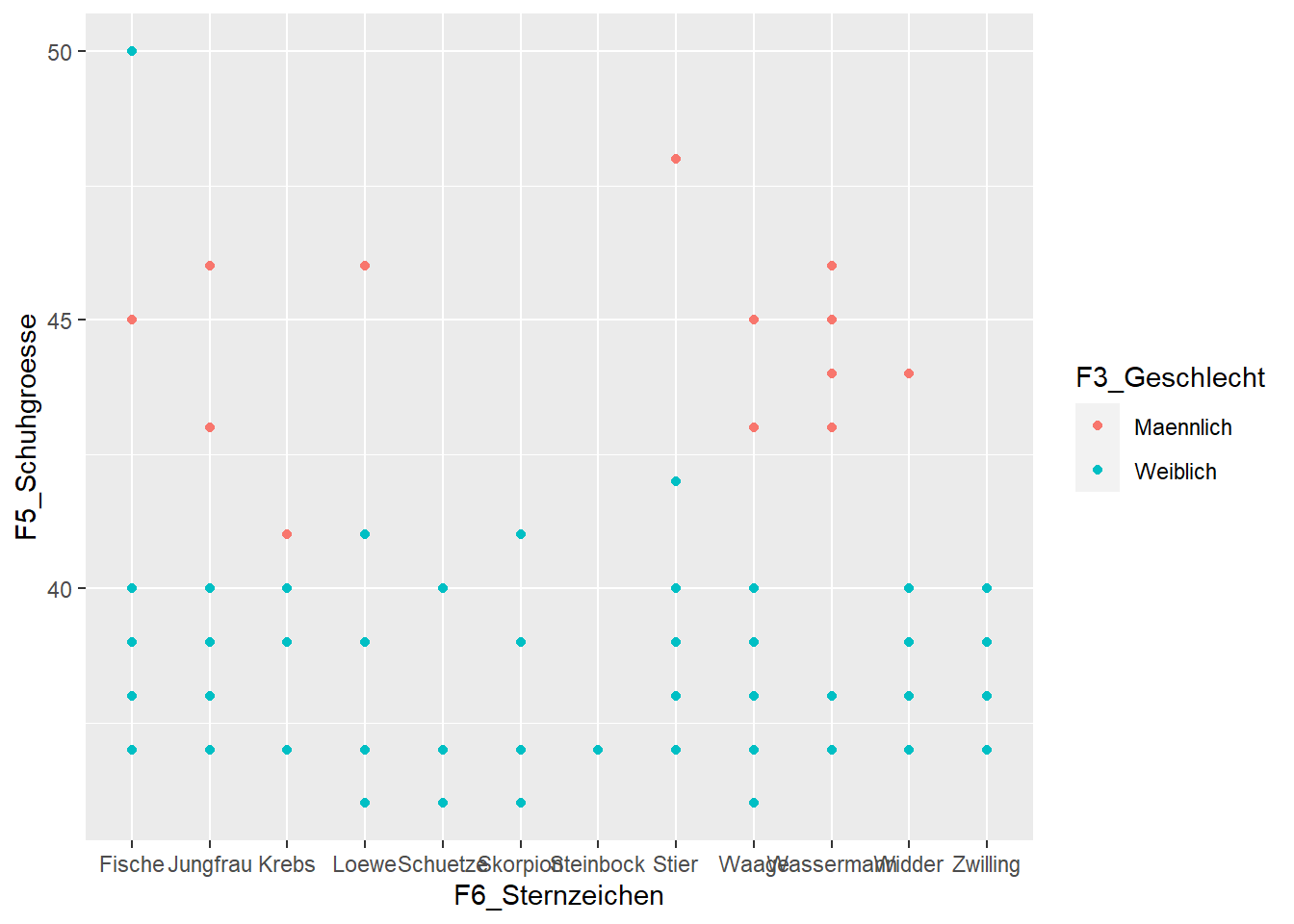
GGplot2 Grafik erstellen
Mit Hilfe von ggplot können wir nun auch detailliertere Grafiken zu unseren WP Studierenden erstellen. Nehmen wir wieder das Schuhgroessen Beispiel aus unserem Datensatz. Der aes() Befehl steht für “Aesthetics” und erwartet als Eingabe einen Vektor. Hiermit definieren wir, was im Folgenden visualisiert werden soll.
Schuhgroesse <- ggplot(data=WPStudis,aes(F5_Schuhgroesse))Jetzt haben wir ggplot2 gesagt, um welche Daten es geht. Um nun etwas anzuzeigen, müssen wir ein “Layer” erzeugen. Dieser nennt sich geom und steht für die geometrische Darstellung der Daten, also ob diese z. B. als Säule oder Linie dargestellt werden sollen. Wir entscheiden uns für ein Säulendiagramm und nutzen daher geom_bar für ein Bar Chart.
Schuhgroesse + geom_bar()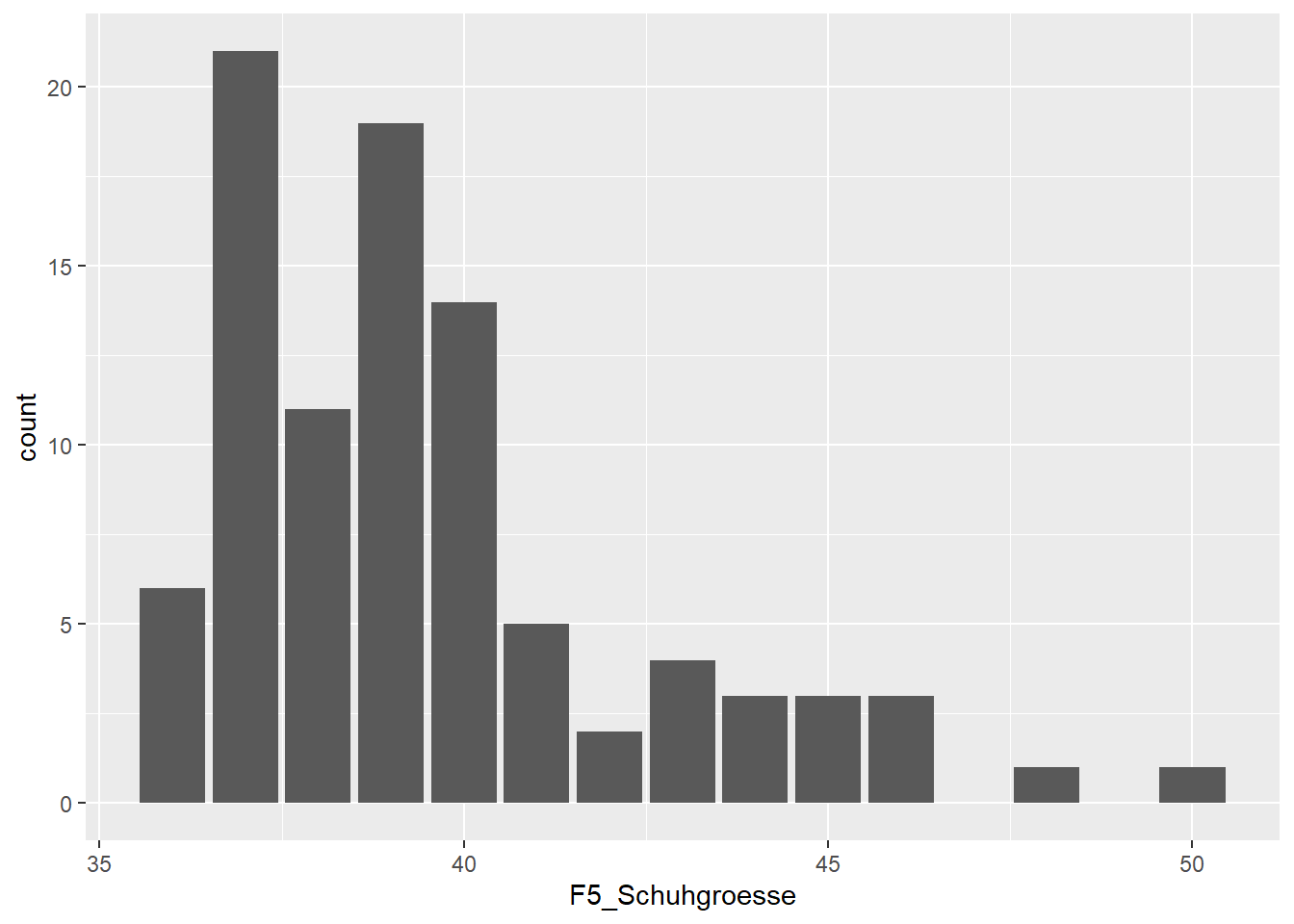
Nun wollen wir die Schuhgroessen nach Geschlecht aufgeteilt darstellen, dazu erzeugen wir ein neues ggplot Objekt und geben nun zwei Variablen ein. Grundsätzlich gilt bei ggplot immer, dass die erste Variable auf der x-Achse und die zweite auf der y-Achse dargestellt wird. Da wir hier die zweite Variable (hier das Geschlecht) nicht als eigenen Achsenwert, sondern als farblich getrennt dargestellt haben wollen, nutzen wir wir das Argument fill.
Schuhgroesse2 <- ggplot(data=WPStudis,aes(F5_Schuhgroesse, fill=F3_Geschlecht))
Schuhgroesse2 + geom_bar()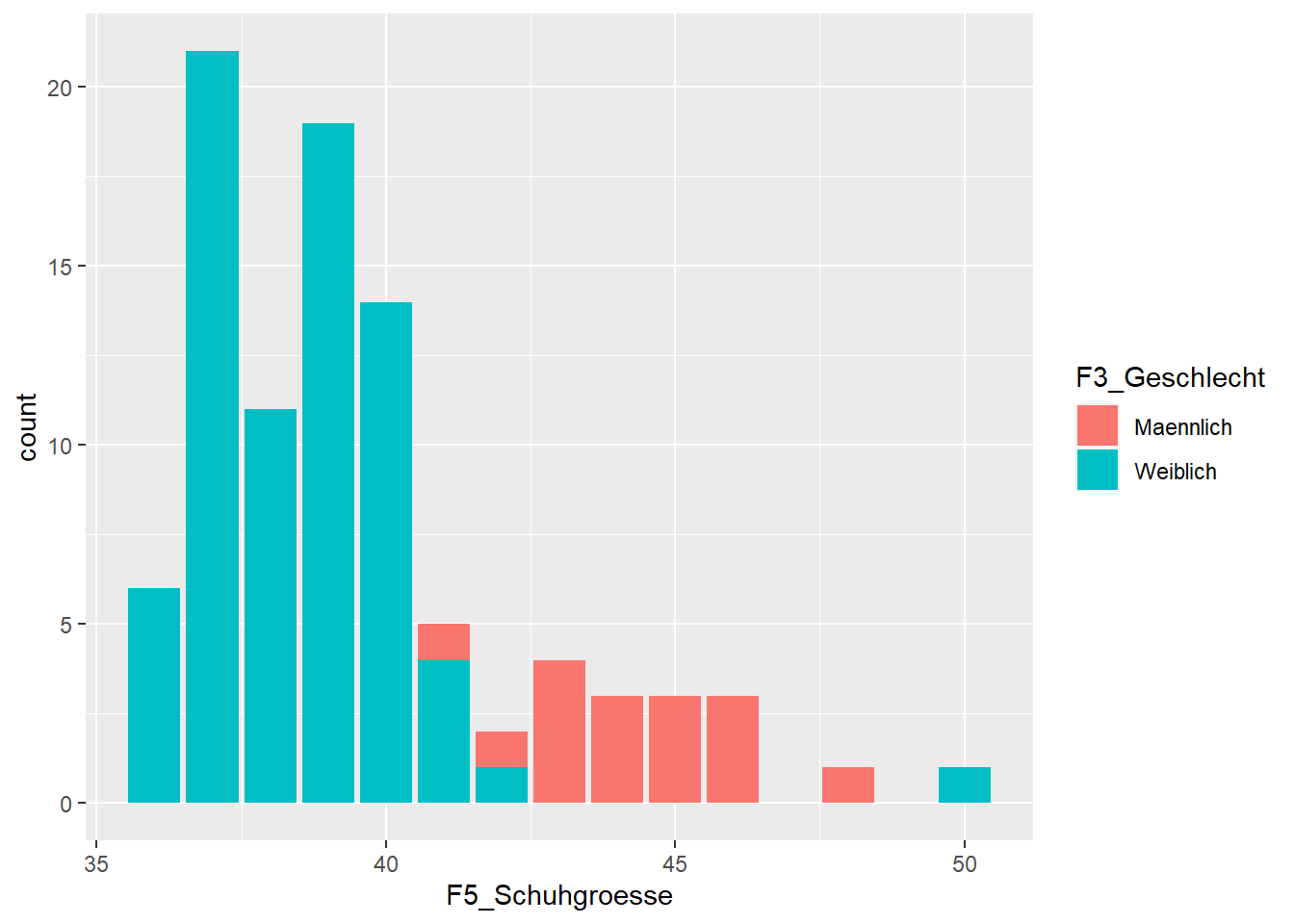
Es gibt eine sehr große Zahl weiterer Darstellungsformen (sog. geoms). In einem weiteren Beispiel erzeugen wir mit dem Argument geom_boxplot einen Boxplot für die gleichen Daten. Da wir jetzt das Geschlecht als Trennung zwischen den beiden Boxplots nutzen wollen, nehmen wir es zuerst und verwenden hier auch nicht das Argument fill.
Schuhgroesse3 <- ggplot(data=WPStudis,aes(F3_Geschlecht,F5_Schuhgroesse))
Schuhgroesse3 + geom_boxplot()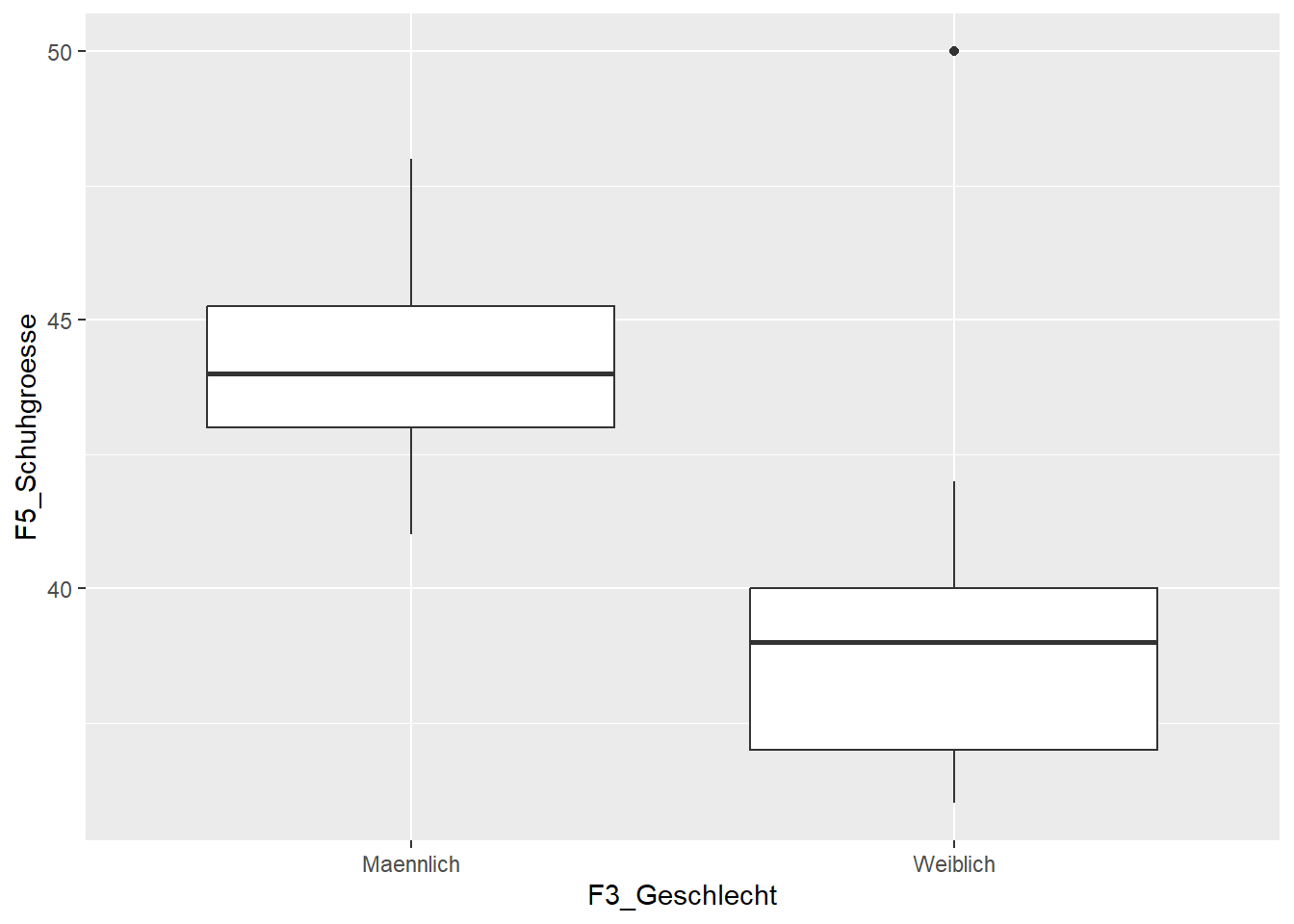
Fehlerbalkendiagramm mit GGPlot2
Nehmen wir nun an, wir wollen nicht die einzelnen Werte darstellen, sondern die Mittelwerte vergleichen. Auch das kann ggplot2. Zunächst müssen wir als x-Achsenwerte Geschlecht und als y-Achsenwerte die Schuhgrösse definieren.
Schuhgroesse_Mittel <- ggplot(data=WPStudis,aes(F3_Geschlecht, F5_Schuhgroesse))Als nächsten benötigen wir hierfür die “stat-summary” Funktion, um die Mittelwerte auszurechnen. Wenn wir uns nun die Grafik ansehen, erhalten wir schon ein Punktdiagramm, welches beide Mittelwerte anzeigt.
Schuhgroesse_Mittel + stat_summary(fun = mean)
## Warning: Removed 2 rows containing missing values
## (`geom_segment()`).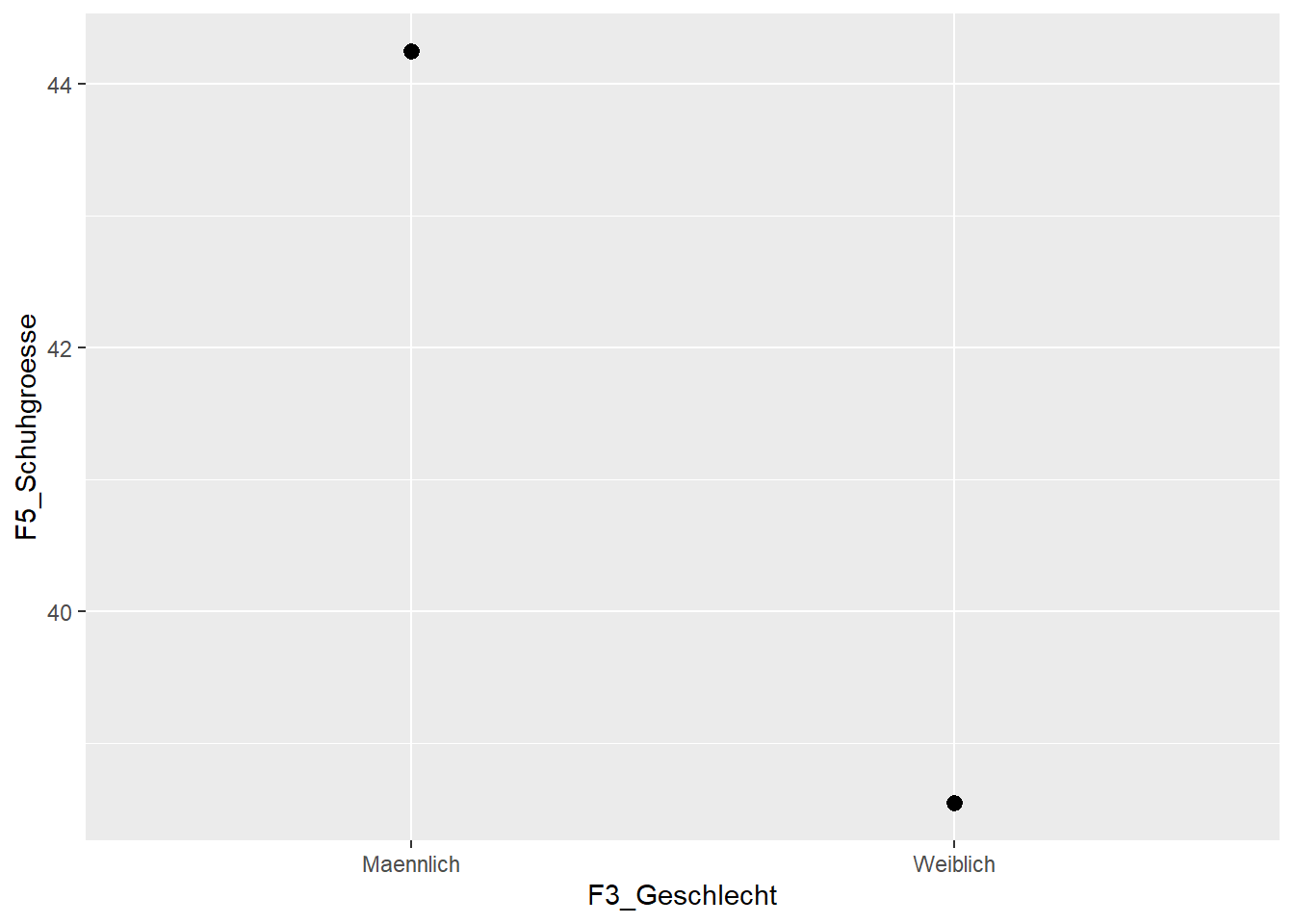
Nun machen wir es noch etwas schöner und beschriften die y-Achse
Schuhgroesse_Mittel + stat_summary(fun = mean) + labs(x="", y="Schuhgroesse")
## Warning: Removed 2 rows containing missing values
## (`geom_segment()`).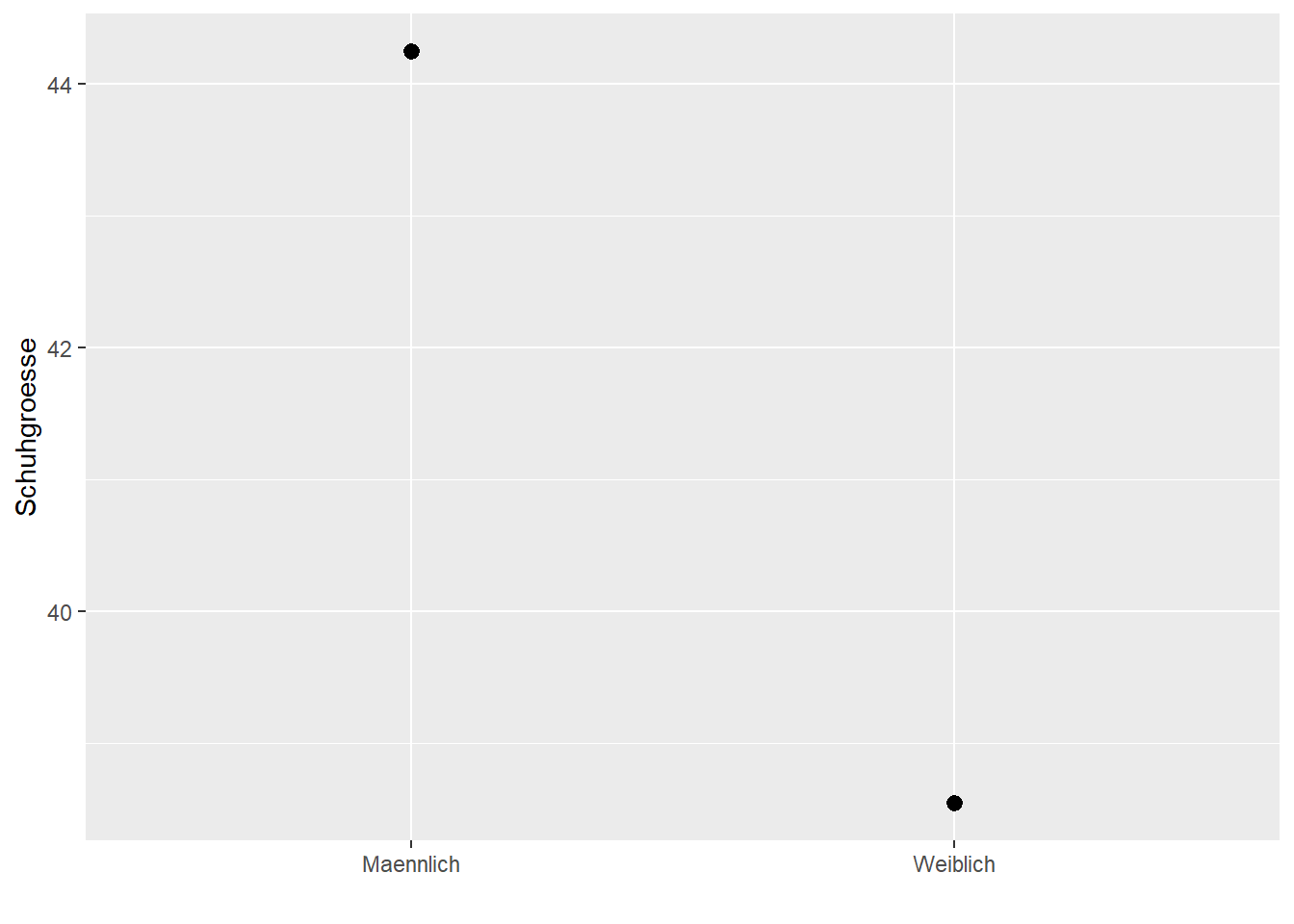
Wir wollen nun zusätzlich die 95 % Konfidenzintervalle anzeigen lassen. Hierzu ergänzen wir die Funktion mean_cl_normal, sowie das geom errorbar (Nur die untere Zeile ist neu)
Schuhgroesse_Mittel + stat_summary(fun = mean ) + labs(x="", y="Schuhgroesse")+ stat_summary(fun.data=mean_cl_normal, geom="errorbar")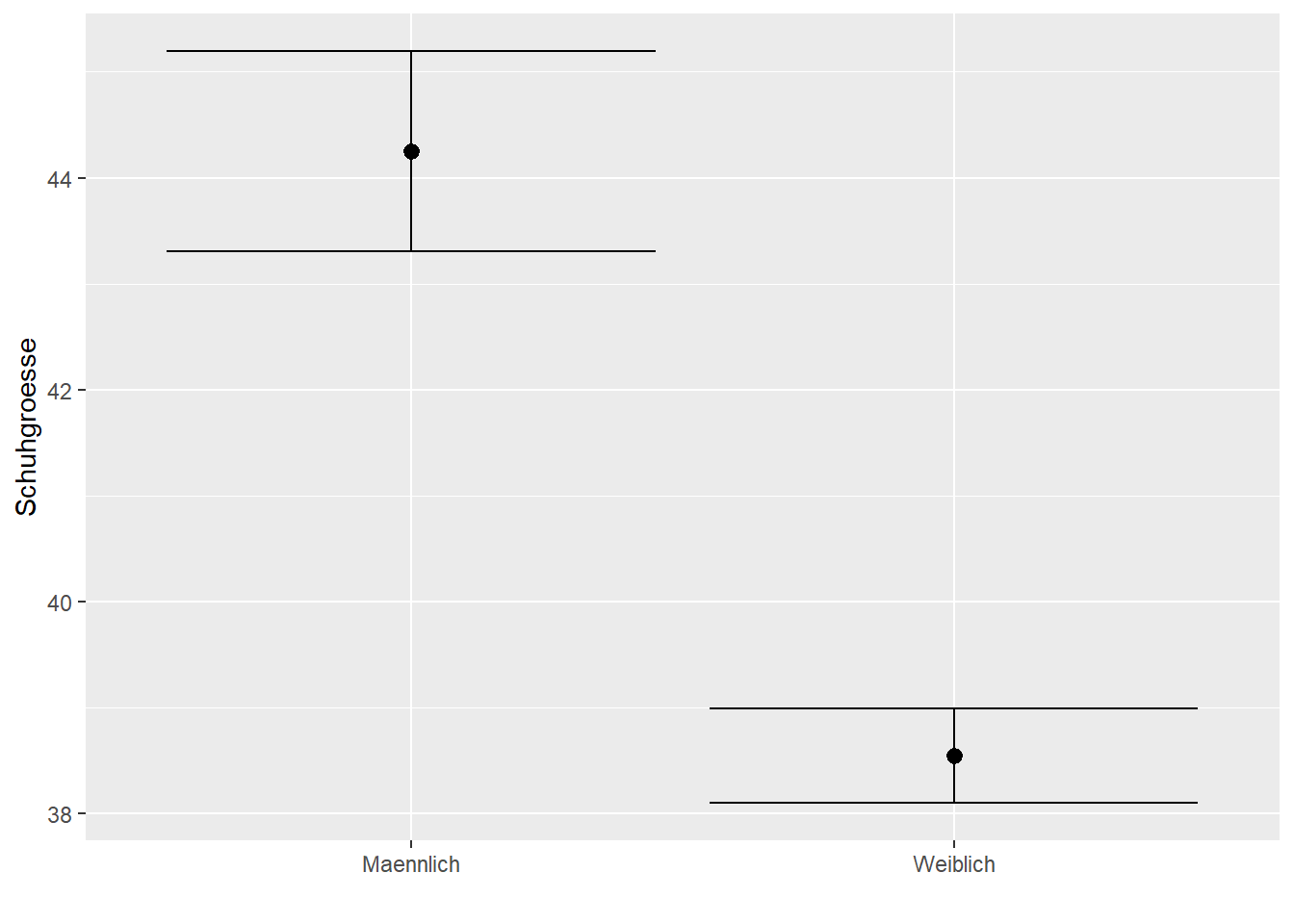
In diesem Video zeige ich, wie das in R funktioniert:
Übung
Erstellen Sie mit ggplot2 ein Histogramm zur Anzahl der Facebook Freunde der WP Studierenden.
Die Lösung zu dieser Übungsaufgabe gibt es im neuen Buch Statistik mit R & RStudio.


