Deskriptive Statistik
3 Häufigkeitstabellen und Diagramme
3.0 Einführung Grafiken
Auch im diesem Kapitel widmen wir uns der Frage, wie wir die Verteilung von Daten möglichst knapp beschreiben und darstellen können. Nachdem wir nun die Kennwerte als mögliche Lösung kennen gelernt haben, wollen wir uns im Folgenden der zweiten Möglichkeit, den Häufigkeitstabellen und Grafiken widmen. Oft werden diese beiden Verfahren in der Praxis auch kombiniert. Neben einer Grafiken werden meist auch die relevanten Kennwerte (Mittelwert und Streuung) mit angegeben.
3.1 Häufigkeitstabellen
Eine Möglichkeit, Daten handhabbarer zu machen, ist darzustellen, wie häufig die einzelnen Merkmalsausprägungen im Datensatz vorkommen. Man spricht in diesem Fall von einer Häufigkeitsverteilung. Dies ist nur möglich für diskrete Verteilungen, also Verteilungen mit klar definierten Kategorien (z.B. Alter in Jahren). Der Vorteil solcher Häufigkeitstabellen ist, dass sie dem Betrachter relativ einfach einen Überblick über die Verteilung bieten. Häufigkeitstabellen sind auch die Basis für die meisten Grafiken, die wir im Folgenden betrachten werden.
Häufigkeiten lassen sich grundsätzlich auf zwei Arten bestimmen:
- Absolute Häufigkeit mit der ein Wert auftritt (Abgekürzt meist f für frequency)
- Relative Häufigkeit in Prozent (Abgekürzt oft f%)
Berechnet wird diese mit (f / n) * 100, wobei n die Anzahl der Werte repräsentiert
Welcher Wert für die Leser hilfreicher ist, hängt vom Untersuchungskontext ab. Meist sind jedoch die prozentualen Häufigkeiten anschaulicher. Wenn ich beispielsweise weiß, dass 42% eines Jahrgangs weiblich sind, dann kann dies direkt interpretiert werden. Mit der absoluten Häufigkeit, beispielsweise 142 Studierende sind weiblich, kann ich diese Information erst interpretieren, wenn ich weiß wie viele Studierende insgesamt vorkommen. Daneben geben Statistikprogramme oft noch die kumulierte prozentuale Häufigkeit an. Hierbei werden aufsteigend alle Prozentwerte aufsummiert.
Beispiel Häufigkeitstabelle
Folgende Tabelle ist eine Häufigkeitstabelle für die Variable Alter von Studierenden in Jahren . Die erste Spalte zeigt die vorkommenden Ausprägungen (Es gibt Personen zwischen 17 Jahren und 21 Jahren im Datensatz). Die zweite Spalte zeigt die absoluten Häufigkeiten, so sind z.B. 3 Studierende 17 Jahre alt und 52 Studierende 21 Jahre alt. Die dritte Spalte gibt die Häufigkeit in Prozent wieder, so können wir z.B. ablesen, dass 40% der Studierenden 19 Jahre alt sind. Die letzte Spalte gibt die kumulierten Prozente an, also die Prozent-Werte von oben nach unten aufsummiert. Hier können wir z.B. ablesen, dass insgesamt rund die Hälfte (genau 52%) der Studierenden 19 Jahre oder jünger ist.
| Alter (in Jahren) | Häufigkeit | Prozent | Kumulierte Prozente |
| 17 | 3 | 1% | 1% |
| 18 | 30 | 11% | 12% |
| 19 | 106 | 40% | 52% |
| 20 | 73 | 28% | 80% |
| 21 | 52 | 20% | 100% |
| Gesamt | 264 | 100% | 100% |
3.2 Kreuztabellen oder Kontingenztabellen
Während die Häufigkeitstabellen nur eine Variable (z.B. das Alter) betrachten, zeigen Kreuztabellen die kombinierten Häufigkeiten von zwei Variablen (z.B. Alter und Geschlecht). In den einzelnen Feldern ist dabei immer die Häufigkeit des gemeinsamen Auftretens von zwei Merkmalen dargestellt (z.B. 17 Jahre und weiblich). Diese Kombinationen der Merkmalsausprägungen wird auch Kontingenz genannt und die Kreuztabelle daher häufig auch als Kontingenztabelle bezeichnet. Diese Häufigkeiten werden ergänzt durch deren Randsummen, die die sogenannten Randhäufigkeiten bilden. Kreuztabellen bieten den Vorteil, dass Sie die Abhängigkeit der Merkmalsausprägungen beider Variablen zeigen, dies werden wir im Kapitel 12 noch vertiefen.
Beispiel 1 Kreuztabelle mit absoluten Häufigkeiten
Folgende Kreuztabelle zeigt das Alter von Studierenden und das jeweilige Geschlecht. In dieser Tabelle sind zunächst nur die absoluten Häufigkeiten angegeben. Die einzelnen Felder zeigen die kombinierten absoluten Häufigkeiten, so sind z.B. 26 Studierende weiblich und 18 Jahre alt. Die Randsummen zeigen die jeweils aufsummierten absoluten Häufigkeiten. Hieraus kann man zum Beispiel ablesen, dass der Studiengang deutlich mehr weibliche Studierende (223) als männliche Studierende (41) hat.
| Alter (in Jahren) | männlich | weiblich | Gesamt |
| 17 | 0 | 3 | 3 |
| 18 | 4 | 26 | 30 |
| 19 | 20 | 86 | 106 |
| 20 | 9 | 64 | 73 |
| 21 | 8 | 44 | 52 |
| Gesamt | 41 | 223 | 264 |
Auch in Kreuztabellen lassen sich relative Häufigkeiten darstellen. Hierbei ist jedoch zu beachten, dass die Prozentwerte entweder zeilenweise oder spaltenweise gebildet werden können. Welche Art der prozentualen Darstellung besser geeignet ist, hängt von der jeweiligen Fragestellung ab. Dies betrachten wir in folgendem Beispiel:
Beispiele 2 Kreuztabelle mit relativen Häufigkeiten
Wir wollen zunächst die relativen Häufigkeiten zeilenweise bilden. In der nachfolgenden Tabellen sehen Sie dass sich jede Zeile zu 100% aufsummiert. Somit können wir z.B. sagen, dass von den Studierenden in der Altersklasse 18 Jahren 13% männlich sind und 87% weiblich. Außerdem gibt uns die letzte Zeile darüber Auskunft wie die Geschlechterverteilung insgesamt ist (16% männlich 84% weiblich).
| männlich | weiblich | Gesamt | |
| 17 | 0% | 100% | 100% |
| 18 | 13% | 87% | 100% |
| 19 | 19% | 81% | 100% |
| 20 | 12% | 88% | 100% |
| 21 | 15% | 85% | 100% |
| Gesamt | 16% | 84% | 100% |
Im nächsten Schritt betrachten wir die gleiche Tabelle mit relativen Häufigkeiten die spaltenweise gebildet wurden. In der nachfolgenden Tabelle summieren sich nicht die Zeile zu 100% auf sondern die Spalten. Aus dieser Tabelle können wir nun z.B. ablesen, dass 49% der männlichen Studierenden 19 Jahre sind oder 20% der weiblichen Studierenden 21 Jahre alt.
| männlich | weiblich | Gesamt | |
| 17 | 0% | 1% | 1% |
| 18 | 10% | 12% | 11% |
| 19 | 49% | 39% | 40% |
| 20 | 22% | 29% | 28% |
| 21 | 20% | 20% | 20% |
| Gesamt | 100% | 100% | 100% |
In den meisten Statistikprogrammen müssen Sie selbst entscheiden, ob die relativen Häufigkeiten zeilen- oder spaltenweise gebildet werden sollen. Überlegen Sie hierfür worauf sie konkret Antworten geben wollen. In diesem Beispiel: Geht es Ihnen im Wesentlichen um die Altersgruppen aufgeteilt nach Geschlecht, dann benötigen Sie zeilenweise Prozente. Geht es Ihnen im Wesentlichen um die Gruppen der männlichen und weiblichen Studierenden aufgeteilt nach Altersgruppen, dann benötigen Sie die spaltenweise Prozente.
Video 3.1 Grafiken Häufigkeitstabellen
3.3 Grafische Darstellung
Graphische Darstellungen von Daten enthalten dieselben Informationen wie Tabellen, sind aber wesentlich anschaulicher. Sie ermöglichen ein schnelles und einfaches Verständnis verschiedener Sachverhalte, bergen dabei aber auch ein gewisses Risiko. Darstellungen können zu verzerrten Interpretationen der Sachlage führen und Effekte entweder visuell verstärken oder abschwächen. Betrachten Sie hierzu zum Beispiel folgende Grafik. Während links klar ein großer Unterschied zwischen A,B,C und D erkennbar ist, sieht es rechts so aus, als ob kaum ein Unterschied vorliegt. In Wirklichkeit zeigen beide Grafiken jedoch die selben Werte, nur die Y-Achse (Ordinate) ist anders skaliert.
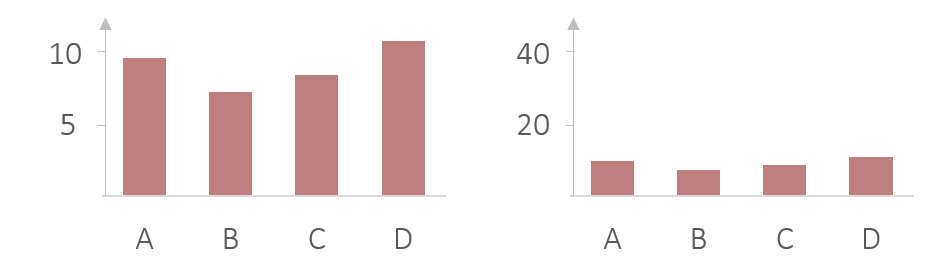
Bei der Erstellung von Grafiken für statistische Zwecke sind daher einige Grundregeln zu beachten.
- Daten sollen gezeigt werden, d.h. die Daten stehen im Mittelpunkt
- Es sollen möglichst viele Daten mit möglichst wenigen graphischen Elementen dargestellt werden
- Möglichst wenig Ablenkung (Keine 3D Effekte, Schatten o.ä. die nicht zur Erklärung der Daten beitragen)
- Es soll klar ersichtlich sein, was dargestellt ist mittels Überschrift, Achsenbeschriftung, Legende, Datenbasis, Erhebungszeitpunkt etc.
- Die Daten sollen so unverzerrt wie möglich dargestellt werden
- Wenn möglich sollte das Diagramm auch ohne Farbdruck lesbar sein
- Der Leser soll dazu animiert werden, sich mit den Daten auseinanderzusetzen (und nicht mit dem Layout des Diagramms).
Diese Regeln gelten für die Anwendung von Grafiken für die Analyse und Erklärung von Daten. Für Werbezwecke kommen solch strenge Regeln in der Regel natürlich nicht zur Anwendung. Achten Sie darauf, wenn Sie das nächste mal eine Werbebroschüre mit bunten Balken oder Kreisen in der Hand halten. Stellen Sie sich dabei immer die Frage inwiefern durch diese Darstellungsform ein bestimmtes Ergebnis suggeriert wird und ob dieses bei einer anderen Form der Darstellung auch so klar herauskommen würde.
3.4 Kreisdiagramm
Das Kreisdiagramm (umgangssprachlich auch Kuchendiagramm genannt), eignet sich für die Darstellung von qualitativen Variablen mit Nominalskalenniveau. Hierbei ist jedoch zu beachten, dass es nicht zu viele verschiedene Ausprägungen geben sollte, da sonst die Lesbarkeit sehr leidet. Für Variablen mit mehr als 5 Ausprägungen ist daher ein Balken- oder Säulendiagramm zu empfehlen, welches wir im Folgenden betrachten.
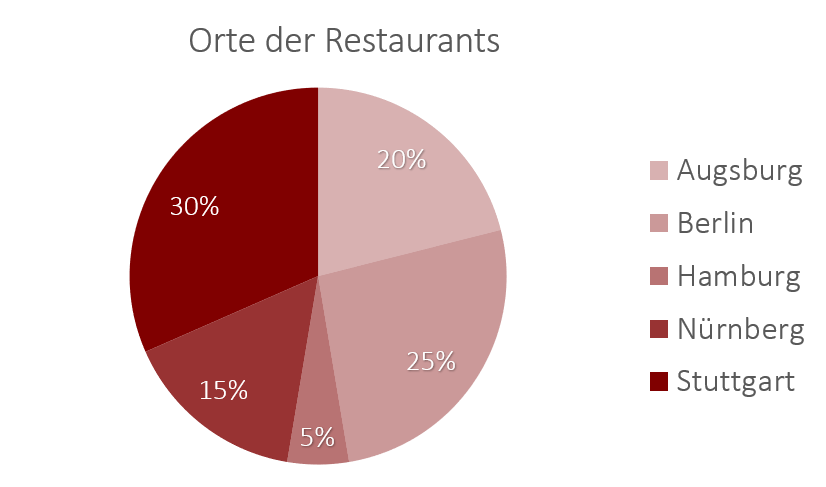
Beispiel Kreisdiagramm
3.5 Balken- / Säulendiagramm
Das Balkendiagramm eignet sich ebenfalls für die Darstellung von Häufigkeiten bei qualitativen Variablen. Sind die Balken nebeneinander dargestellt, spricht man üblicherweise von einem Säulendiagramm. Sind diese übereinander angeordnet, spricht man von einem Balkendiagramm. Der Vorteil dieser Darstellungsform ist, dass durch die übersichtliche Darstellung der Balken neben- oder übereinander die Unterschiede zwischen den Häufigkeiten der einzelnen Ausprägungen direkt ersichtlich werden. Beispielsweise sieht man in den beiden Grafiken unten sofort, dass in Berlin mehr Restaurants sind als in Augsburg, während im Kreisdiagramm zuvor dieser kleine Unterschied nur schwer abzulesen ist.
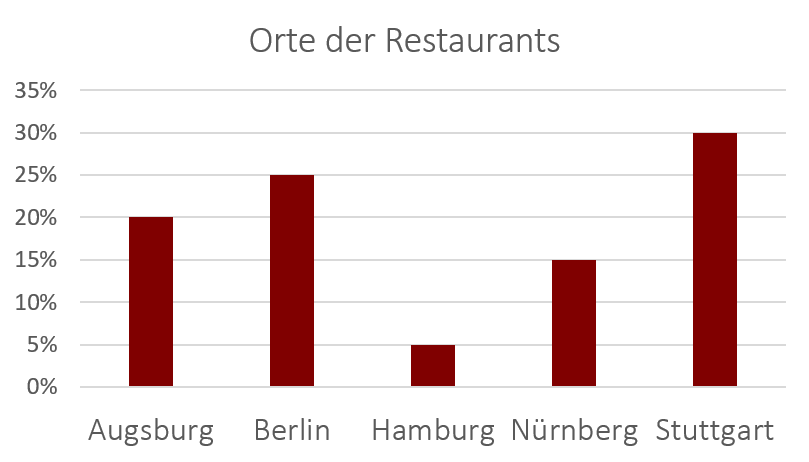
Beispiele für Säulen- und Balkendiagramme
Das unten abgebildete Säulendiagramm enthält die gleichen Informationen wie das Kreisdiagramm zuvor. Jedoch sind hier die relativen Anteile deutlich leichter abzulesen (z.B. 15% der Restaurants in Nürnberg)
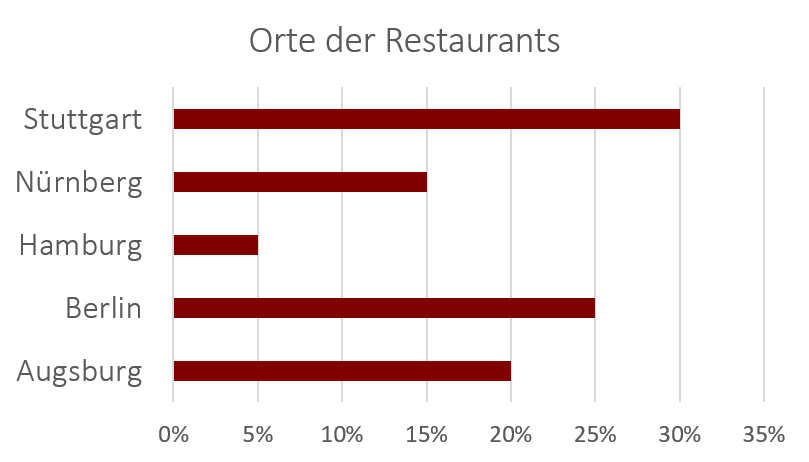
Alternativ zum Säulendiagramm können die Balken auch horizontal dargestellt werden. In diesem Fall handelt es sich um ein Balkendiagramm.
3.6 Gruppierte und Gestapelte Säulendiagramme
Wir haben nun zwei Möglichkeiten kennen gelernt Häufigkeitstabellen grafisch darzustellen. In der Praxis kommt es jedoch häufig vor, dass auch Kreuztabellen in einer Grafik dargestellt werden sollen. Es gilt nun also noch mehr Informationen in einer Grafik darzustellen. Hierfür gibt es wieder zwei Möglichkeiten: Stapeln oder Gruppieren.
Gestapelte Säulendiagramme basieren auf der Idee der kumulierten prozentualen Häufigkeiten, die wir am Anfang dieses Kapitels besprochen haben. Das heißt die Prozentwerte einer Variablen (meist der mit mehr Ausprägungen) werden kumuliert in nur einem Balken mit unterschiedlichen Farben dargestellt. Nachteil dieser Darstellungsform ist dabei, dass die Farbunterschiede (grade beim Druck) oft schlecht erkennbar sind. Überdies sind kleinere Unterschiede in den Häufigkeiten nur schwer interpretierbar, da der Startpunkt der Abschnitte unterschiedlich ist.
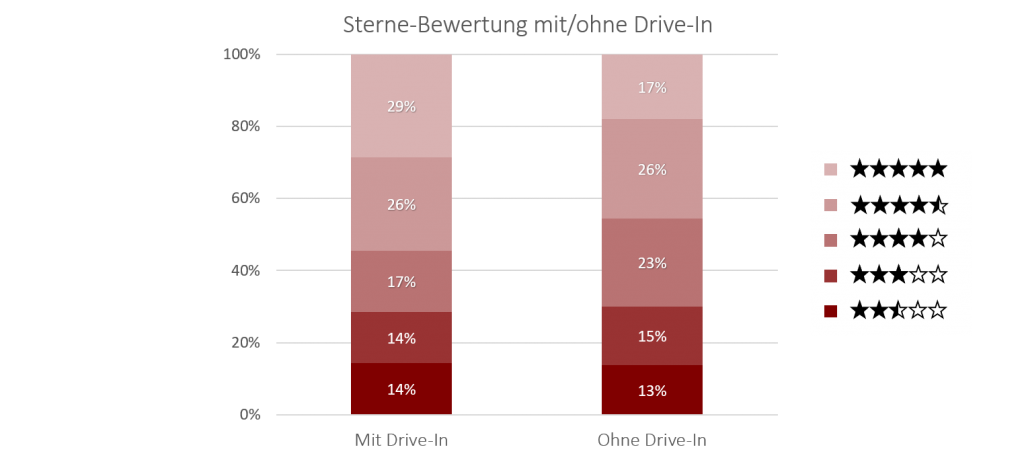
Beispiel gestapeltes Säulendiagramm
Beispiel für ein gestapeltes Säulendiagramm bezogen auf die Anzahl der Sterne Bewertung von Burger-Restaurants in Google (2.5 – 5 Sterne) kombiniert mit der Variable Drive-In (Vorhanden / Nicht Vorhanden). Zentrale Tendenzen lassen sich hierbei gut erkennen, zum Beispiel dass Restaurants mit Drive in 29% 5-Sterne Bewertungen haben und Restaurants ohne Drive-In nur 17% 5-Sterne Bewertungen.
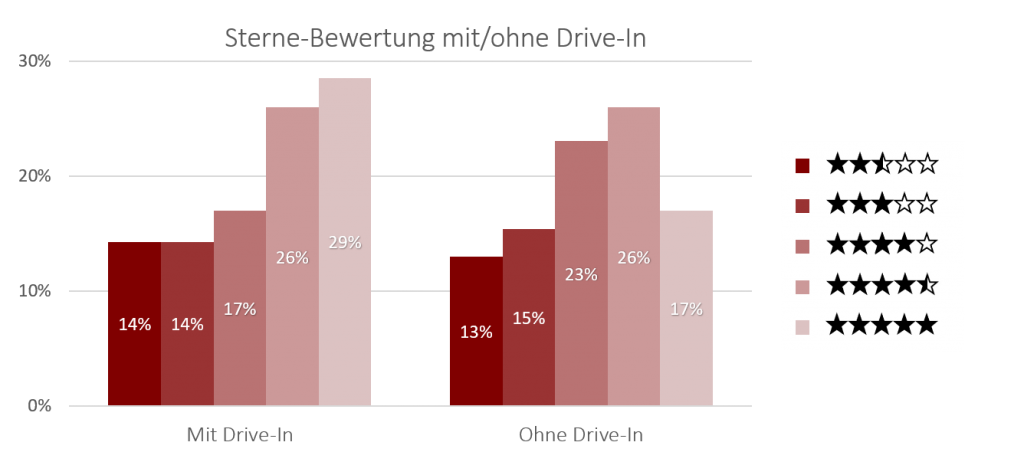
Gruppierte Säulendiagramme entsprechen einem normalen Säulendiagramm mit dem Unterschied, dass sie nicht die Häufigkeit der Merkmale einer Variable darstellen (z.B. Haarfarben), sondern das gemeinsame Auftreten von Merkmalen auf zwei Variablen (z.B. Haarfarben nach Geschlecht aufgeteilt). Hierbei wird für jede Ausprägung der einen Variable eine Säule erstellt, die dann nach den Ausprägungen der anderen Variable gruppiert werden. Dies hat den Vorteil, dass die Höhe der Säulen stets direkt vergleichbar und damit gut interpretierbar ist.
Beispiel gruppiertes Säulendiagramm
Das unten stehende gruppierte Säulendiagramm enthält die gleichen Informationen wie im Beispiel zuvor. Durch die Anordnung der Balken nebeneinander lassen sich jedoch auch kleine Häufigkeitsunterschiede sehr leicht erkennen.
3.7 Liniendiagramm
Eine weitere Variante des Säulen- / Balkendiagramms ist das Liniendiagramm. Der Aufbau ist ähnlich, jedoch wird anstatt eines Balkens eine Linie eingezeichnet, die die einzelnen Werte verbindet. Der Vorteil ist hierbei, dass auch mehrere Linien übereinander gelegt werden können und somit auch die Daten aus Kreuztabellen dargestellt werden können, analog zu gruppierten Balkendiagrammen. Der Nachteil dieser Darstellungsform ist zum einen, dass die Linien suggerieren, dass die einzelnen Werte zusammengehörig sind und zum anderen, dass es auch Werte zwischen den Ausprägungen gibt. Beides ist aber oft in der Realität nicht der Fall.
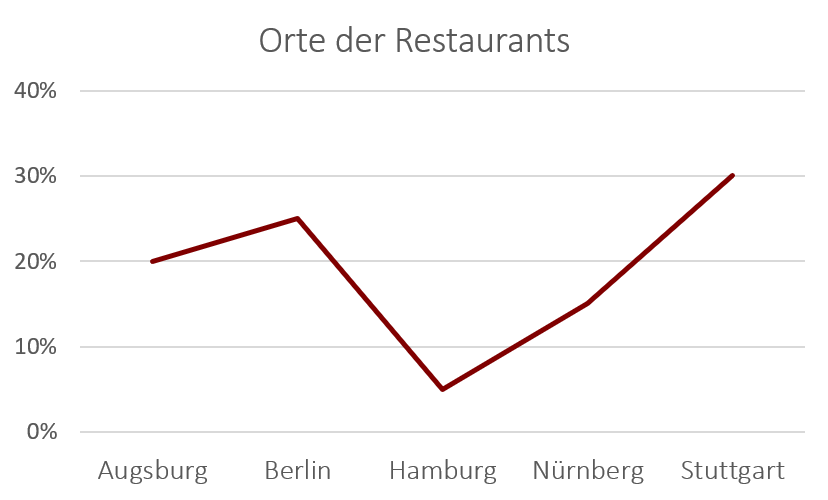
Beispiel Liniendiagramm
Das folgende Beispiel zeigt ein Liniendiagramm wieder für den Anteil unserer Burger-Filialen in verschiedenen Städten. Die Darstellungsform hat im Vergleich zum Säulendiagramm den Nachteil, dass sie suggeriert, dass es Werte zwischen den einzelnen Städten gibt, was natürlich in der Realität nicht der Fall ist.
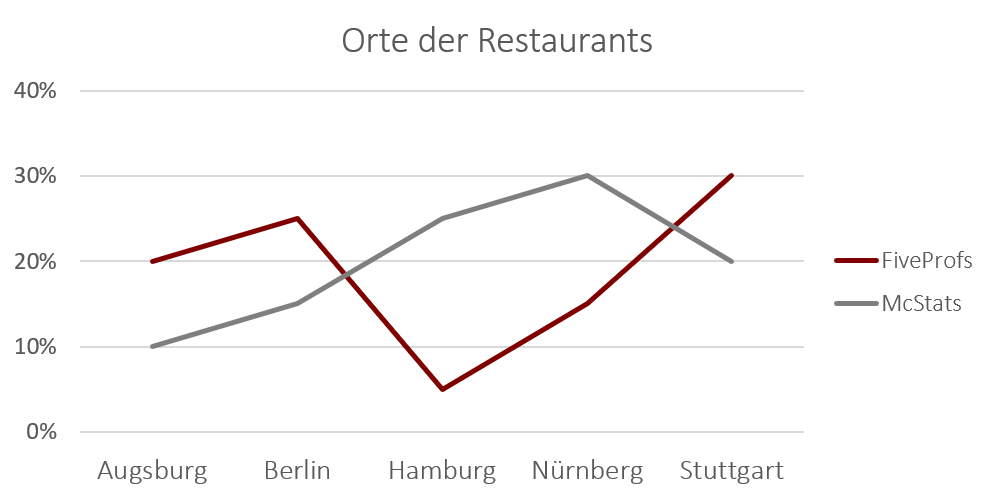
Das folgende Beispiel zeigt ein Liniendiagramm für zwei Variablen (Ort und Burger-Kette). Diese Darstellungsform wird auch Profildiagramm genannt und hat den Vorteil, dass die Häufigkeiten von zwei oder mehr Ausprägungen einer anderen Variable (hier die zwei Burger-Ketten) direkt miteinander verglichen werden können. Eine Alternative hierzu wäre ein gruppiertes Balkendiagramm.
3.8 Fehlerbalkendiagramm
Werden metrische Variablen betrachtet z.B. die Größe von Studenten oder der Umsatz je Filiale, so lassen sich hierbei keinen Häufigkeiten mehr darstellen (da die Anzahl der Balken sehr hoch werden würde). Daher wollen wir im folgenden graphische Darstellungsmöglichkeiten für solche Variablen betrachten. Wir beginnen mit der einfachsten Darstellungsform, dem Punktdiagramm, wobei der Mittelwert (arithmetisches Mittel) einer Variablen als einfacher Punkt dargestellt wird. Wie wir im letzten Kapitel bereits gelernt haben, sollte dieser Kennwert immer um ein Streuungsmaß ergänzt werden um dem Leser ein realistisches Bild der Verteilung zu geben. Üblicherweise wird daher neben dem Punkt noch die Standardabweichung eingezeichnet, die angibt wie weit die Werte im Mittel um den Mittelwert streuen. Diese wird mit feinen Linien und jeweils einer Begrenzung eingezeichnet, die als Barthaare oder aus dem Englischen als Whisker bezeichnet werden. Alternativ wird bei dieser Darstellungsform auch oft der Standardfehler mit eingezeichnet, welchen wir im Kapitel Parameterschätzung noch kennenlernen werden. Daher sollte immer mit angegeben werden, welcher dieser beiden Kennwerte mit den Barthaaren dargestellt wird.
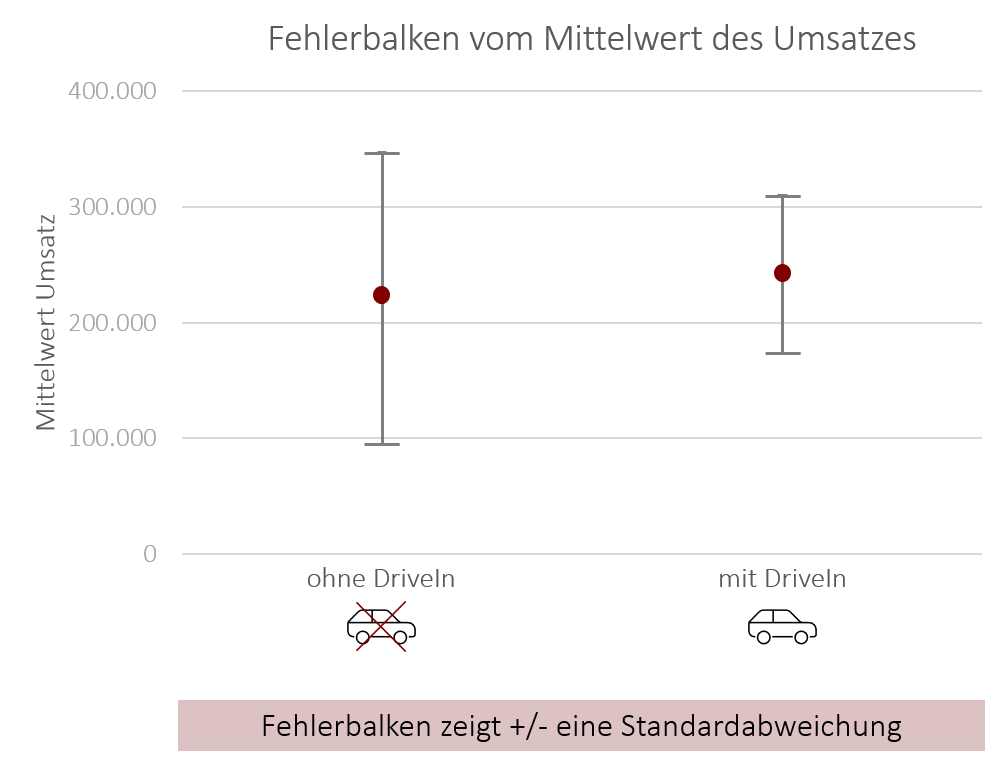
Beispiel Fehlerbalkendiagramm
Das unten stehende Punkt-Diagramm mit Fehlerbalken, oder kurz Fehlerbalken-Diagramm, zeigt das arithmetische Mittel des Umsatzes unserer Burger-Filialen, geteilt in Filialen mit Drive-In und ohne Drive-In. Hier lässt sich erkennen, das Filialen mit Drive-In einen leicht höheren mittleren Umsatz generieren. Zusätzlich zeigen die Whisker in diesem Fall die jeweilige Standardabweichung. Diese wird grafisch auf den Mittelwert addiert und davon subtrahiert. Der resultierende Bereich innerhalb der schwarzen Linien zeigt also die durchschnittliche Streuung um den Mittelwert. In diesem Fall kann man erkennen, dass bei Burger-Filialen ohne Drive-In eine größere Streuung des Umsatzes vorliegt als bei Burger-Filialen mit Drive-In.
3.9 Streudiagramm
Geht es nicht darum, die Verteilung von zwei Variablen, sondern deren Zusammenhang darzustellen, kommt das sogenannte Streudiagramm (englisch: Scatterplot) zum Einsatz. Diese Darstellungsform bietet sich an, wenn beide Variablen metrisch skaliert sind. Anders als in den bisherigen Darstellungsformen werden bei Streudiagrammen keine Häufigkeiten dargestellt, sondern jeder einzelne Wert bzw. jedes kombinierte Wertepaar eines Merkmalsträgers wird als einzelner Punkt dargestellt. Wenn wir beispielsweise die Größe und das Gewicht von Personen in einem Streudiagramm darstellen wollen, dann entspricht jeder Punkt einer Person und die Lage des Punktes wird im zweidimensionalen Raum durch die zwei Werte (Größe und Gewicht) festgelegt. Der große Vorteil dieser Darstellungsform ist, dass der Zusammenhang zwischen zwei metrischen Variablen sehr schön visuell dargestellt wird. Hierauf werden wir im Kapitel Korrelation zurückkommen.
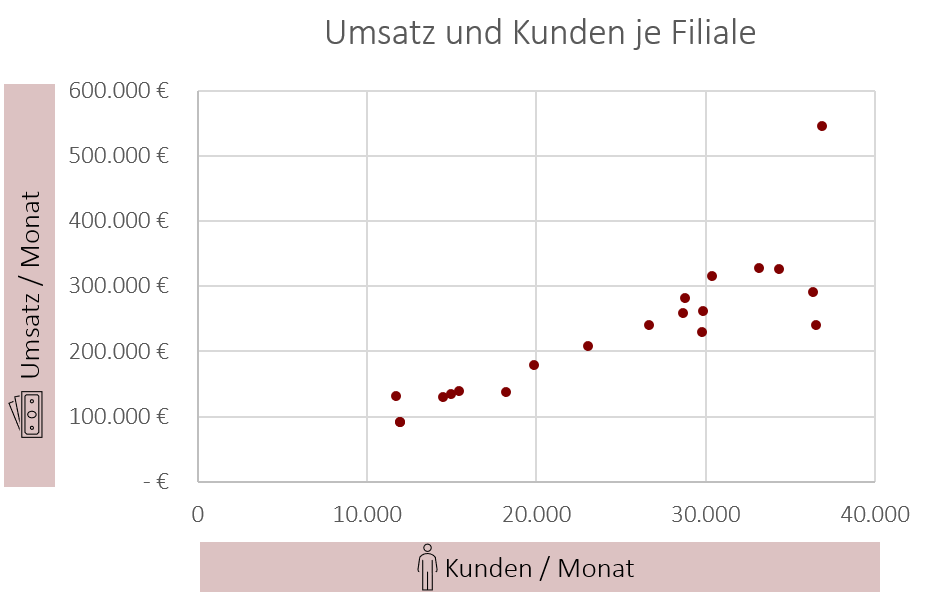
Beispiel Streudiagramm
Im folgenden Streudiagramm zeigt jeder rote Punkt eine unserer Burger-Filialen. Die Position des Punktes wird auf der X-Achse durch die Anzahl der Kunden und auf der Y-Achse durch den Umsatz (jeweils pro Monat) festgelegt. Ausblick: Wenn die Punkte einem klaren Trend folgen, wie hier von links unten nach rechts oben, dann bedeutet dies, dass es auch einen Zusammenhang zwischen den Variablen gibt. Im vorliegenden Beispiel ist dieser recht einfach zu erklären: Filialen mit mehr Kunden pro Monat machen auch mehr Umsatz pro Monat und vice versa. Auf das Thema Zusammenhänge zwischen Variablen werden wir im Kapitel Korrelation näher eingehen.
Video 3.2 Grafiken Diagrammtypen
3.10 Boxplot
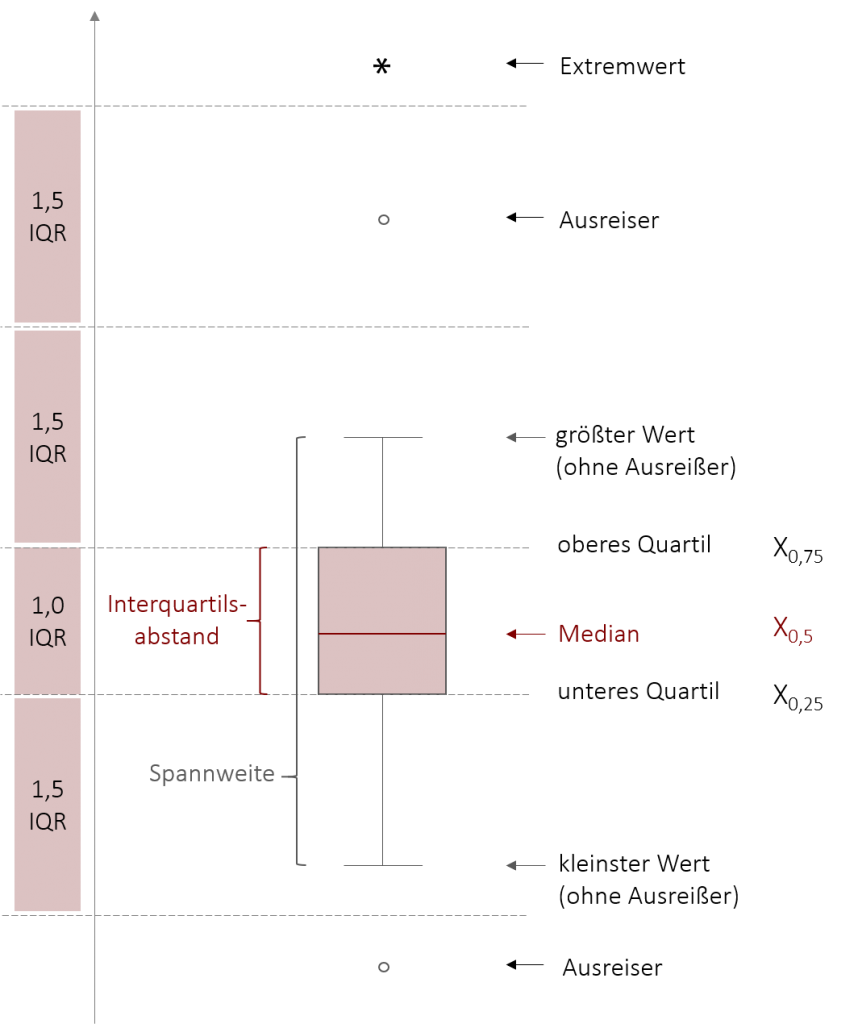
Eine weitere beliebte Darstellungsform in der Statistik ist der Boxplot (seltener auch Box-Whisker-Plot genannt). Dieser kann dazu genutzt werden die Verteilungsform einer metrisch skalierten Variable zu visualisieren. Der Boxplot bietet dabei sehr viele Informationen in kompakter Form. Die Linie in der Mitte zeigt den Median der Verteilung an. Die Box zeigt den Interquartilsabstand, also den Bereich in dem die Mittleren 50% der Werte liegen. Darüber hinaus zeigen die Barthaare (auch Whisker genannt) die Spannweite, also den Bereich aller Werte, mit Ausnahme der Ausreißer. Im Boxplot sind Ausreißer definiert als alle Werte die mehr als 1,5 Interquartilsabstände von der Box entfernt sind. Hinweis: In SPSS, werden neben Ausreißern auch sogenannte Extremwerte angezeigt, diese sind weiter als 3 Interquartilsabstände von der Box entfernt. Der Vorteil dieser Darstellungsform ist, dass die Darstellung der Verteilung nicht durch Ausreißer verzerrt wird und gleichzeitig die Ausreißer jedoch nicht unterschlagen werden, sondern explizit in der Grafik dargestellt werden.
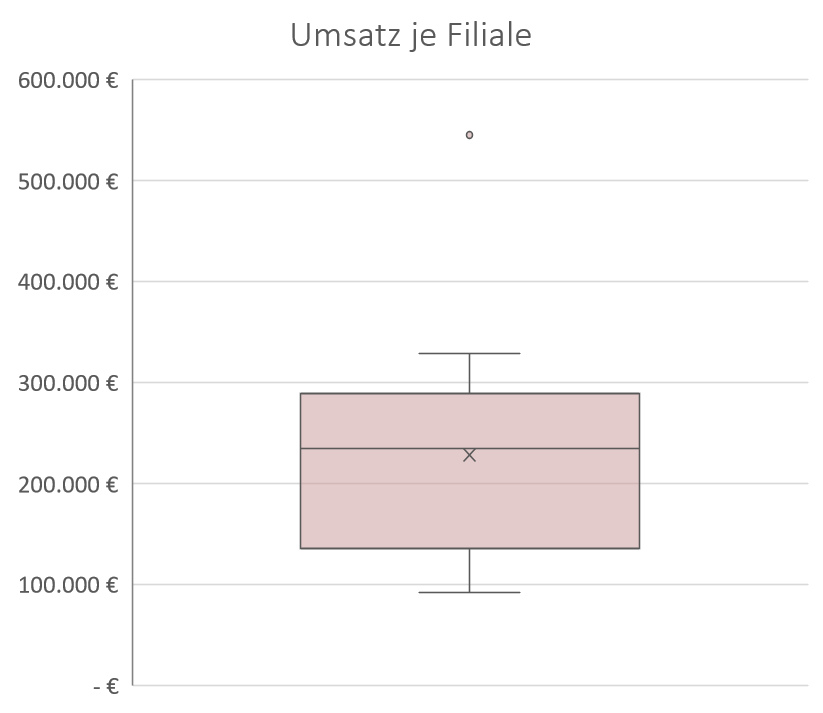
Beispiel Boxplot
Der unten stehende Boxplot zeigt die Verteilung für den Umsatz je Burger-Filiale pro Monat. Die mittlere Linie zeigt den Median, also den „mittleren Umsatz“, von ca. 240 t€. Die Box zeigt den Interquartilsabstand von ca. 140 t € bis ca. 290 t€, also ca. 150 t€. Wir können nun also sagen, dass die Hälfte unserer Burger-Filialen zwischen 140 t € und 290 t€ Umsatz pro Monat machen. Die Barthaare von ca. 100 t€ bis ca. 330 t € zeigen die Spannweite, also alle Werte ohne den einen Ausreißer, der als Punkt einzeln bei ca. 550 t€ dargestellt wird. Wir können nun also sagen, dass unsere Burger-Filialen zwischen 100 t€ und 330 t € Umsatz pro Monat machen, es jedoch eine Filiale gibt die deutlich mehr Umsatz macht. Ab wann wird hier ein Wert als Ausreißer bezeichnet? Die Rechnung hierfür ist recht simpel, man nimmt den Interquartilsabstand mal 1,5 (also 150 t€ * 1,5 = 225 t€) und addiert diesen Wert auf die Box, die bei ca. 290 t€ Endet. Das bedeutet, dass für diesen Boxplot alle Werte über 515 t€ als Ausreißer bezeichnet werden.
Video 3.3. Grafiken Der Boxplot
3.11 Histogramm
Alternativ zum Boxplot können Verteilungen auch in einem sogenannten Histogramm dargestellt werden. Auch diese Darstellungsform eignet sich um die Verteilungsform einer metrisch skalierten Variable mit vielen Ausprägungen zu visualisieren. Das Histogramm sieht auf den ersten Blick aus wie ein normales Säulendiagramm, bietet diesem gegenüber jedoch einige entscheidende Vorteile. Würde man z.B. die Körpergröße in einem einfachen Säulendiagramm darstellen, so würde jede potenzielle Merkmalsausprägung (üblicherweise in cm) einen Balken bekommen. Dadurch wäre die Darstellung schon mal ziemlich unübersichtlich. Erschwerend kommt hinzu, dass Merkmalsausprägungen, die nicht vorkommen, einfach ausgelassen werden. Dadurch entsteht eine nicht einheitliche Skalierung auf der X-Achse (weil z.B. der Wert 176 einfach fehlt). Das Histogramm löst beide Probleme auf eine sehr einfache Art: Die Skalierung auf der X-Achse ist fest (z.B. cm aufsteigend) und die Werte werden in gleich große Klassen zusammengefasst. Diese Klassen sind feste Intervalle im Wertbereich der Variable (z.B.: je 10 cm). Innerhalb der Klassen wird dann wieder die Häufigkeit gezählt, die entweder in absoluten Werten oder prozentualen Werten auf der Y-Achse dargestellt wird. Die Größe dieser Klassen kann beliebig festgelegt werden, wobei die meisten Statistikprogramme die Klassen automatisch so einteilen, dass 10-15 Balken entstehen. Der größte Vorteil dieser Darstellungsform, ist dass die Verteilungsform unverzerrt dargestellt wird. Hierdurch lässt sich die Form der Verteilung mit bekannten Verteilungen wie der Normalverteilung vergleichen. Hierzu mehr im nächsten Kapitel.
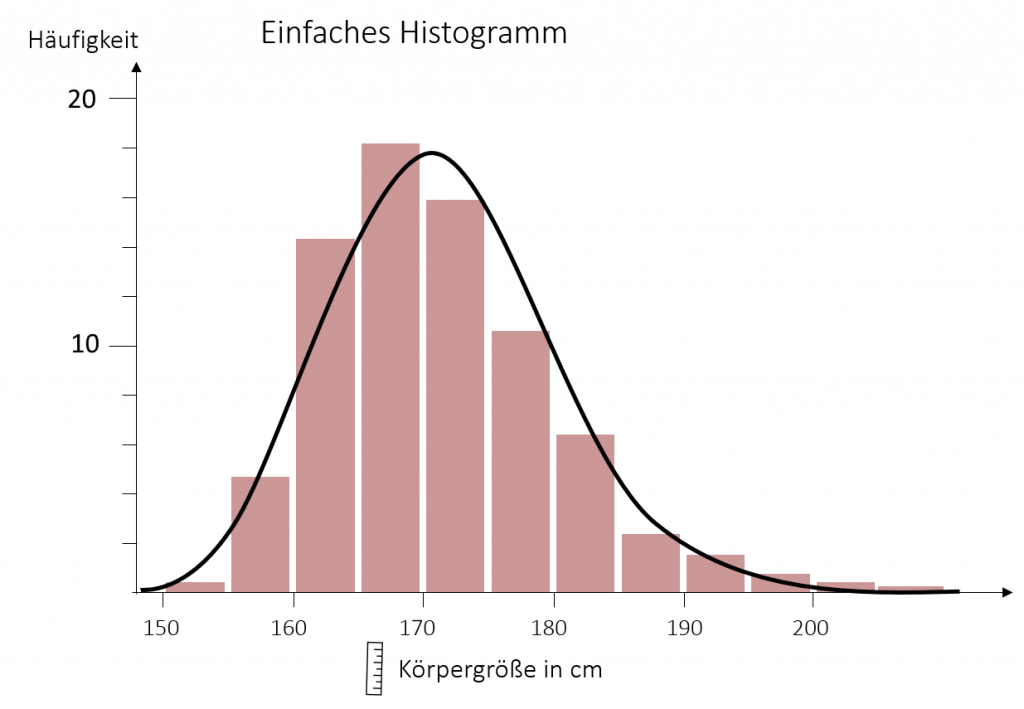
Beispiel Histogramm
Das folgende Histogramm zeigt die Verteilung der Körpergröße einer Stichprobe unserer Mitarbeiter. Zusätzlich ist die Normalverteilung eingefügt. Die Breite der Klassen wurde in diesem Beispiel manuell auf je 5 cm festgelegt. Die Y-Achse zeigt in diesem Fall die absoluten Häufigkeiten. Hierdurch lassen sich sehr leicht visuell Häufigkeiten ablesen. Man kann zum Beispiel ablesen, dass 16 Mitarbeiter zwischen 170 und 175 cm sind. Die Verteilungsform folgt ungefähr der Normalverteilung, scheint aber leicht nach links verschoben. Wie man dies genauer interpretiert lernen Sie im folgenden Kapitel.
3.12 Beurteilung der Schiefe und Kurtosis
Wir haben nun gelernt, dass uns das Histogramm erlaubt, die Verteilungsform einer Variablen sehr gut zu visualisieren. Im Folgenden wollen wir uns noch damit beschäftigen, wie man die Verteilungsform einer Variablen in Worten beschreiben kann. Verteilungen können sehr unterschiedlich aussehen. Nehmen wir hierzu als Beispiel die Altersverteilung in der Bevölkerung. In Europa ist diese aktuell sehr ausgeglichen, der größte Anteil der Bevölkerung ist im mittleren Alter und die Verteilung nimmt in beide Richtungen ab (es gibt weniger junge und alte Menschen). In Uganda sieht diese Verteilung jedoch ganz anders aus, hier sind knapp 50% der Bevölkerung unter 15 Jahre alt. Man könnte also sagen die Verteilung ist hin zu den jüngeren Altersklassen verschoben. Um nun eine einheitliche Sprachregelung für eine solche Beschreibung von Verteilungen zu finden, wird in der Statistik jede Verteilung zunächst mit der Normalverteilung verglichen. Wie wir im vorigen Kapitel bereits gesehen haben, bietet jedes Statistikprogramm die Möglichkeit, die jeweilige Normalverteilung direkt in das Histogramm einzuzeichnen. Zur Erinnerung: Es gibt nicht die eine feste Normalverteilung. Für jede Verteilung wird eine eigene Normalverteilung erzeugt, die durch zwei Parameter ebendieser Verteilung festgelegt ist: Dem arithmetischen Mittel und der Standardabweichung.
Im nächsten Schritt wird die Verteilungsform (also die Säulen des Histogramms) mit der Normalverteilung verglichen. Abweichungen können hierbei in zwei Dimensionen auftreten: horizontal (die Verteilung neigt sich nach rechts oder links) oder vertikal ( die Verteilung ist spitziger oder flacher als die Normalverteilung). Bei der horizontalen Abweichung spricht man von der Schiefe der Verteilung, bei der vertikalen Abweichung von der Kurtosis der Verteilung. Beidem wollen wir uns nun genauer widmen.
Schiefe der Verteilung
Die Schiefe einer Verteilung beschreibt, ob eine Verteilung symmetrisch ist oder sich zu einer Seite neigt (Neigungsstärke). Bei einer schiefen Verteilung liegen die häufigsten Ausprägungen nicht in der Mitte der Antwortskala, sondern auf einer Seite. Dies kann entweder nach rechts oder nach links der Fall sein . Entsprechend wird unterschieden zwischen:
- Positive Schiefe: Die Verteilung neigt sich nach links, d.h. geht nach rechts weiter als nach links (auch rechtsschief bzw. linkssteil)
- Negative Schiefe: Die Verteilung neigt sich nach rechts, d.h. geht nach links weiter als nach rechts (auch linksschief bzw. rechtssteil)
Die Schiefe der Verteilung wird in Statistik-Programmen auch mit einem numerischen Wert ausgegeben. Hierbei bedeutet ein negativer Wert eine negative Schiefe und ein positiver Wert eine positive Schiefe. Größere Werte bedeuten das eine größere Abweichung von der Normalverteilung vorliegt.
Kurtosis der Verteilung
- Positive Kurtosis: Schmaler Gipfel (engl. leptokurtic)
- Negative Kurtosis: Breiter Gipfel (engl. platykurtic)
Auch für die Kurtosis wird in Statistik-Programmen ein numerischer Wert ausgegeben, bei dem ebenfalls gilt: Positiver Wert bedeutet eine positive Kurtosis und vice versa.
Beschreibung der Verteilungsform
Wenn Sie zukünftig also eine Verteilung beschreiben, können Sie ihr neues Vokabular anwenden und können diese sowohl im Hinblick auf die Schiefe als auch im Hinblick auf die Kurtosis beschreiben. Das folgende Beispiel soll dies verdeutlichen.
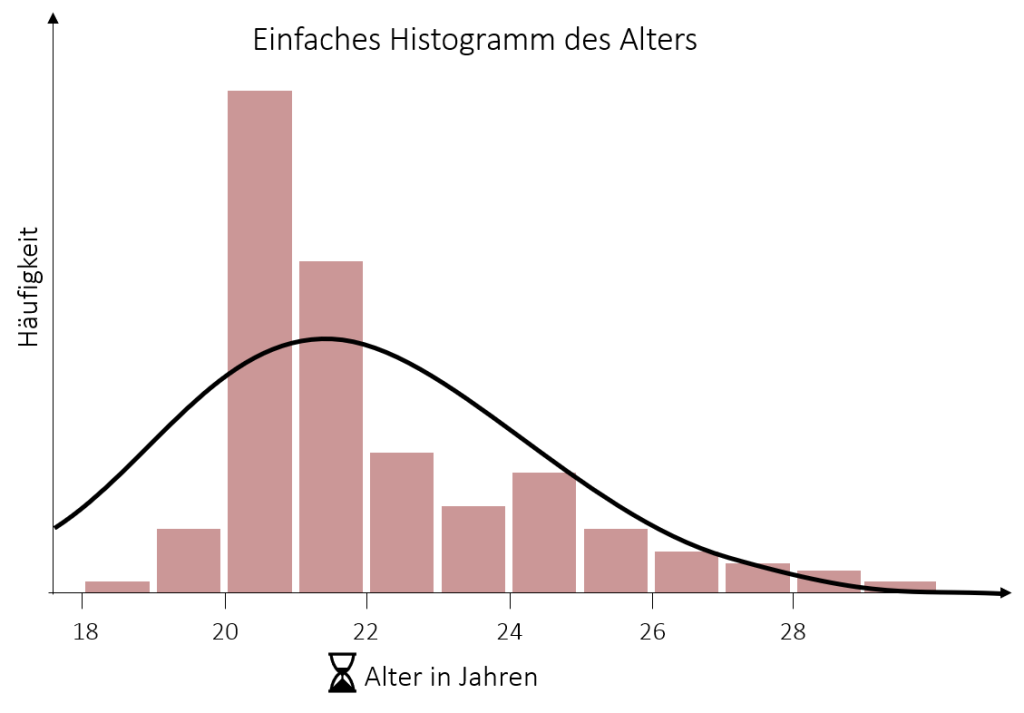
Beispiel Beurteilung der Verteilungsform
Das folgende Histogramm zeigt die Altersverteilung unserer Mitarbeiter, sowie die dazugehörige Normalverteilung. Die tatsächliche Verteilung (Balken) weicht erheblich von der Normalverteilung ab (Linie). Da die Balken sich nach links neigen, also links steiler sind und rechts stark abfallen, liegt hier eine positive Schiefe vor. Leicht ersichtlich ist auch, dass die Verteilung eine deutliche Spitze bei rund 20 Jahren hat und damit auch eine positive Kurtosis gegeben ist. Das heißt die Verteilung ist deutlich schmalgipfliger als die Normalverteilung.
Video 3.5 Grafiken Verteilungsform
3.13 Übersicht über Grafiken
Oft ist es nicht einfach zu entscheiden welche Darstellungsform nun die geeignetste ist. Die folgende Tabelle soll Ihnen hierfür eine Hilfestellung bieten.
| 1 Variable | 2 Variablen | |
| Häufigkeiten (meist bei qualitativen Variablen) | Balken-/Säulen-Diagramm Kreisdiagramm |
Gruppiertes oder gestapeltes Säulen-Diagramm |
| Zentrale Tendenzen (bei metrischen Variablen) | Boxplot Histogramm Fehlerbalken-Diagramm |
Boxplots Fehlerbalken-Diagramm |
| Zusammenhänge | – | Streudiagramm |
3.14 Häufigkeitstabellen und Kreuztabellen in SPSS
Darstellen von Häufigkeitstabellen
Darstellung von Kreuztabellen
3.15 Mehrfachantwortensets in SPSS
3.16 Grafiken in SPSS erstellen
In SPSS gibt es viele Möglichkeiten Grafiken bzw. Diagramme zu erzeugen. Hierfür gibt es einen recht komfortablen Grafikassistent, der unter folgendem Menü gefunden werden kann.
Grafik > Diagrammerstellung
In diesem Menü können Sie zunächst per „Drag and Drop“ den gewünschten Diagrammtyp auswählen. Es gibt neben den klassischen Balkendiagramm eine große Auswahl an typischen Darstellungsformen, wie Kreis- oder Liniendiagramme, sowie typische statistische Diagrammtypen wie Histogramme, Boxplots oder Fehlerbalkendiagramme. Der gewählte Diagrammtyp wird dabei im Vorschaufenster schematisch angezeigt und es gibt dort die Möglichkeit die anzuzeigenden Variablen wieder per Drag and Drop direkt auf die Achsen zu ziehen. Wie das genau funktioniert wird im folgenden Video erläutert.
3.9 Grafiken in SPSS erstellen für eine Variable
Oft ist es das Ziel von Diagrammen die kombinierte Auftretenshäufigkeit von zwei Variablen darzustellen. Beispielsweise den durchschnittlichen Umsatz aufgeteilt nach Geschlecht oder Altersgruppen. Hierfür bieten sich Punktdiagramme, sowie gestapelte und gruppierte Balkendiagramme an. Wie diese in SPSS erzeugt werden können wird im folgenden Video erläutert.
3.10. Grafiken in SPSS für zwei Variablen erstellen
Wenn Sie Grafiken in R erstellen wollen, dann finden Sie hier meinen R-Kapitel zu diesem Thema.
3.17 Übungsfragen
Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!
In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!



