Zusammenhänge und Vorhersagen
6 Z-Standardisierung
6.0 Einführung
6.1 Berechnung des Z-Werts
Man berechnet hierzu die relative Abweichung, indem man die Abweichung vom Mittelwert in Einheiten der jeweiligen Standardabweichung darstellt. Hierdurch erhalten Werte unterschiedlicher Skalen ein einheitliches Format (den sogenannten Z-Wert) und können direkt miteinander verglichen werden. Das Ergebnis ist die Z-Standardisierung oder auch Z-Transformation.
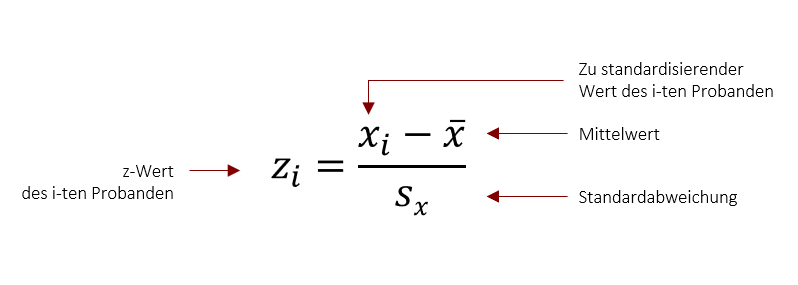
Der resultierende Z-Wert ermöglicht somit eine universell interpretierbare Aussage darüber, wie weit ein Wert vom Mittelwert entfernt ist. Ein Wert von +3 bedeutet hierbei zum Beispiel, dass die Person drei Standardabweichung vom Mittelwert entfernt ist.
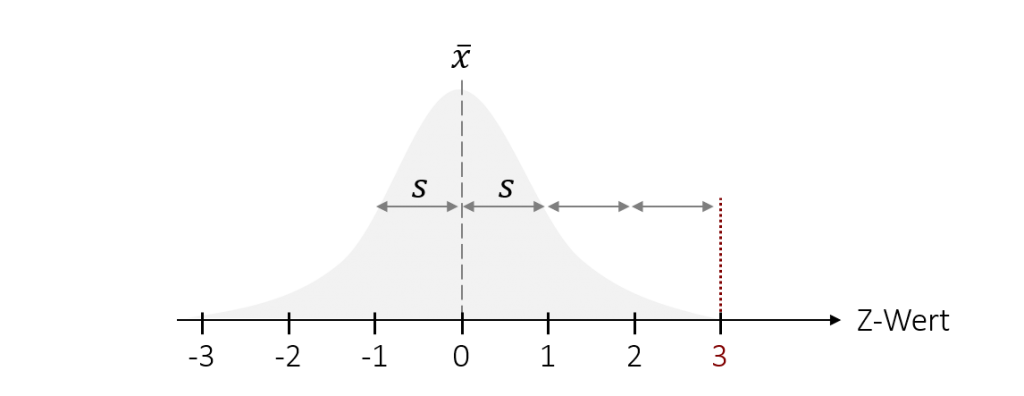
Da die Standardabweichung die durchschnittliche Streuung repräsentiert, bedeutet dies auch, dass die meisten Werte im Bereich +/- eine Standardabweichung um den Mittelwert liegen (mehr dazu in Kapitel 6.3). Ein Z-Wert von+ 3 ist daher schon ein sehr ungewöhnlicher Wert – also ein Ausreißer. Der Z-Wert kann hierbei positive und negative Werte annehmen. Die Interpretation des Vorzeichens hängt dabei von der zugrundeliegenden Skala ab. Nehmen wir als Beispiel die Punkte in der Statistik-Klausur. Hier würde ein Z-Wert von 3 bedeuteten, dass die Person ein extrem gutes Ergebnis erzielt hat (deutlich mehr Punkte wie die meisten anderen, die dieselbe Klausur geschrieben haben). Wäre die zugrunde liegende Skala das Notensystem (1 sehr gut – 6 ungenügend), dann würde ein Wert von +3 bedeuten, dass die Person ein sehr schlechtes Ergebnis (eine schlechtere Note als die meisten anderen) erzielt hat.
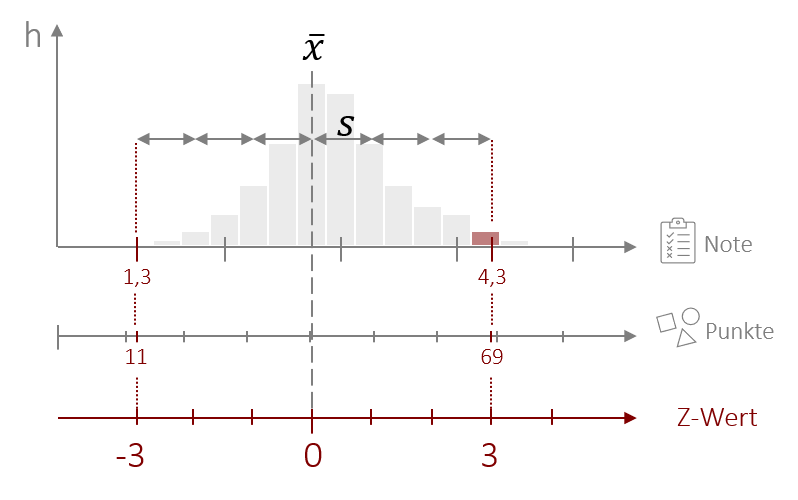
Beispiel Z-Standardisierung
Zwei Schulkameraden haben an der PISA-Studie teilgenommen, Peter im Fach Deutsch, Jakob im Fach Mathematik. Beide haben einen Wert von 620 Punkten erreicht. Nun möchten sie herausfinden, wer von beiden relativ besser abgeschnitten hat. Hierfür bringen die beiden zunächst die Kennwerte der PISA-Ergebnisse für Deutschland in Erfahrung. Diese sind:
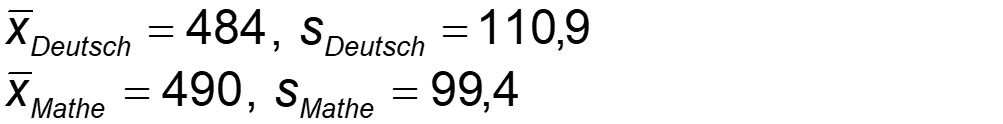
Im Folgenden können wir nun die jeweiligen z-Werte für beide errechnen. Die Berechnung hierfür lautet:
![]()
![]()
Wie können wir nun die beiden Z-Werte Interpretieren?
Beide Schüler haben in ihren Fächern überdurchschnittlich gut abgeschnitten. Aber obwohl Peters Ergebnis auf der (ursprünglichen) Punkteskala deutlicher vom Mittelwert abweicht, ist Jakobs Ergebnis (im Vergleich mit allen deutschen Schülern) als besser zu beurteilen. Es liegt um 1,31 Standardabweichungen oberhalb vom Mittelwert; Peters Ergebnis liegt mit 1,23 Standardabweichungen weniger weit vom Mittelwert entfernt. Jakob hat damit das relativ bessere Ergebnis im PISA-Test erreicht.
6.2 Transformation von Verteilungen
Mit der Z-Standardisierung lassen sich nicht nur einzelne Werte, sondern auch ganze Verteilungen standardisieren. Hierdurch wird jede beliebige Verteilung, in eine Verteilung mit dem Mittelwert 0 und der Standardabweichung 1 transformiert. Man spricht auch von einer Zentrierung der Daten, da dadurch die Verteilung immer in gleich viele positive, wie negative Werte aufgeteilt wird. Dabei gehen natürlich die Werte auf der Ursprungsskala verloren, d.h. Sie können danach zum Beispiel nicht mehr direkt ablesen, wer welche Punktzahl oder Note erreicht hat. Die relative Position der Werte und damit auch die Verteilungsform der Verteilung bleibt jedoch erhalten. Dies hat unter anderem den Vorteil, dass Verteilungsformen mit unterschiedlichen Ausgangsskalen (also z.B. Noten, Punkte etc.) verglichen werden können.
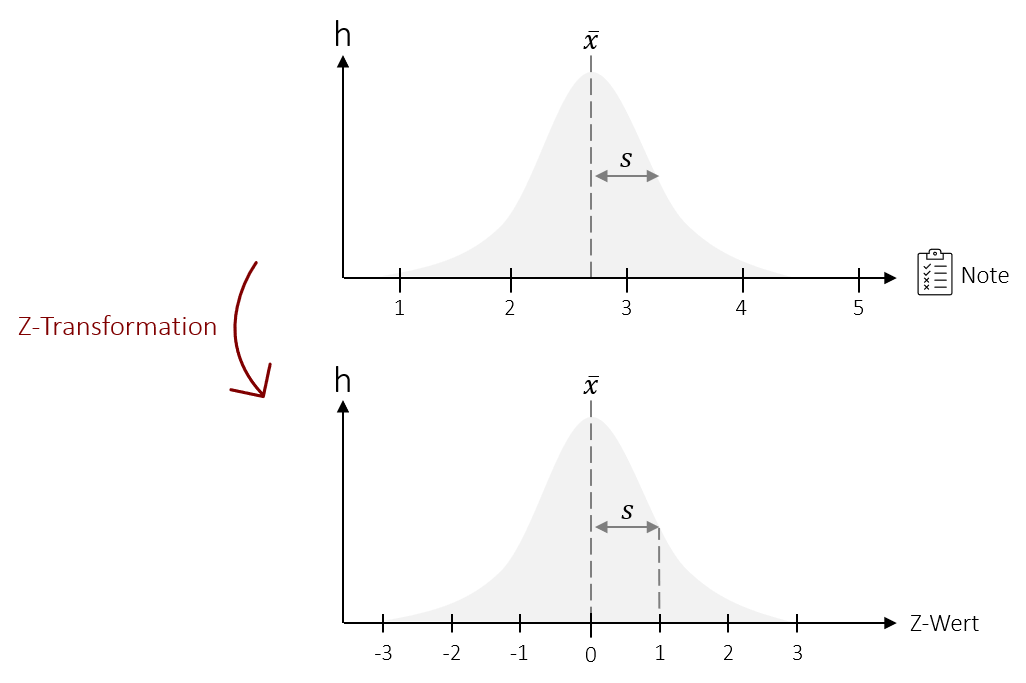
Video 6.2 Z-Standardisierung | Transformation
6.3 Die Standardnormalverteilung
Die Normalverteilung kommt in der Natur sehr häufig vor: das Gewicht von Kühen, die Größe von Bäumen, aber auch die Intelligenz von Menschen, all dies ist normalverteilt. Dabei beschreibt die Normalverteilung nur die Form der Verteilung. Der genaue Verlauf der jeweiligen Normalverteilung wird durch den Mittelwert und die Standardabweichung bestimmt. Hierdurch ergibt sich eine Besonderheit, denn wenn wir eine beliebige Normalverteilung standardisieren kommen wir immer bei exakt der gleichen Verteilung heraus: Der sogenannten Standardnormalverteilung. Einer Normalverteilung mit Mittelwert 0 und Standardabweichung 1.
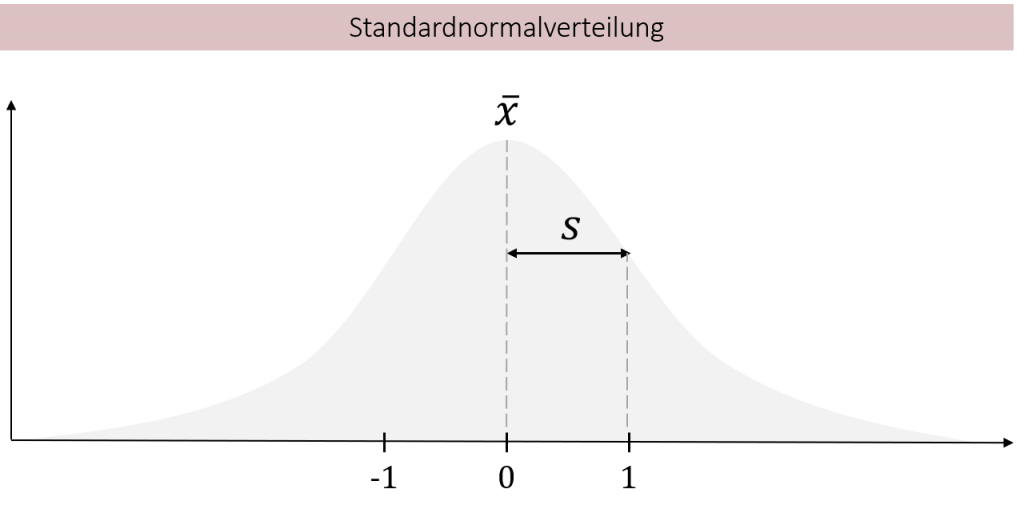
Da diese Verteilung immer exakt gleich ist, lässt sich ihr Verlauf sehr genau beschreiben. Grundsätzlich können wir, über die Berechnung von Integralen, die Flächen unter dieser Funktion exakt bestimmen und können damit die Häufigkeiten, mit denen Werte in bestimmten Intervallen auftreten, festlegen. Da diese Werte jedoch immer gleich sind, müssen wir nicht jedes mal ein Integral rechnen, sondern wir können die Werte bequem aus Tabellen ablesen, die Sie z.B. im Anhang zu fast allen Statistikbüchern finden.
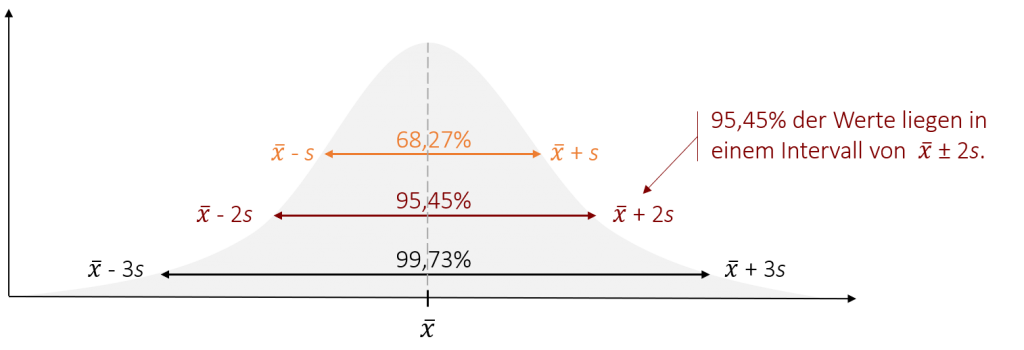
Wichtige Intervalle, die Sie kennen sollten:
- Zwischen +1 und -1 Standardabweichung liegen rund 2/3 der Werte (genau 68,27%)
- Zwischen +2 und -2 Standardabweichungen liegen rund 95% der Werte (genau 95,45%)
- Zwischen +3 und -3 Standardabweichungen liegen über 99% der Werte (genau 99,73%).
Dies hat ganz praktische Anwendungen. Nutzen wir als Beispiel hierfür wieder die Person, die bei einem Test einen Z-Wert von 3 erreicht hat. Wir haben bereits gesagt, dass ein Z-Wert von 3 sehr selten ist und es sich um einen Ausreißer handelt. Dies können wir nun genauer spezifizieren. Wenn wir nun weiter wissen, dass die Testergebnisse (annährend) normalverteilt sind, dann können wir ableiten, dass jemand mit einem Z-Wert von 3 auf jeden Fall zu den allerbesten in dem jeweiligen Test gehört hat. Denn einen Z-Wert von 3 erreichen nur 100%-99,73% also 0,27%. Dieser Wert ist jedoch immer noch zu Groß, denn er beinhaltet noch den Bereich von unter -3 und den Bereich größer als 3 (also die Schlechtesten und Besten in dem Test). Wenn wir diesen Wert halbieren, haben wir die die tatsächliche Häufigkeit, die wir bei einem beliebigen (normalverteilten) Test für den Bereich größer als z=3 erwarten. Dieser ist 0,27% /2 also nur 0,135%. Wir können nun also sagen, dass der Kandidat mit seinem Z-Wert von 3 schon zu den ca. 0,1% besten im Test gehört, was wirklich eine tolle Leistung ist.
Diese Berechnungslogik wird im nun folgenden Kapitel – der Inferenzstatistik – von sehr großer Bedeutung sein. In folgendem Video wird diese daher nochmal kurz erläutert.
Video 6.3 Z-Standardisierung | Standardnormalverteilung
6.4 Z-Standardisierung in SPSS
Für die Berechnung eines Z-Wertes werden sowohl Mittelwert, als auch Standardabweichung einer Verteilung benötigt. Beide Kennwerte lassen sich zwar händisch berechnen, doch ist es in den meisten Fällen komfortabler dies mit einer Statistiksoftware wie SPSS zu machen. Die Berechnung beider Kennwerte ist über folgendes Menü möglich:
Analysieren > Deskriptive Statistiken > Deskriptive Statistik
Das Men bietet jedoch auch die Möglichkeit automatisch alle Werte einer Verteilung in Z-Werte umzurechnen und diese als neue Variable anzulegen. Hierzu machen Sie einfach einen Haken bei „Standardisierte Werte als Variablen speichern“ und im Folgenden wird für jede gewählte Variable eine neue, standardisierte Variable angelegt.
Video 6.4 Z-Standardisierung in SPSS berechnen
6.5 Übungsfragen
Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!
In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!
6.6 Übungsaufgaben



