Deskriptive Statistik
1 Grundlagen
1.0 Grundlagen – Zeit Vokabeln zu lernen
Zunächst die schlechte Nachricht: Sie werden in nächster Zeit viele neue Begriffe lernen müssen. Statistiker und Daten-Analysten sprechen eine eigene Sprache, die für Außenstehende oft abschreckend wirkt. Die gute Nachricht ist jedoch, dass sich diese „Sprache“ deutlich leichter erlernen lässt als jede Fremdsprache, da die Anzahl der Vokabeln überschaubar ist und sich dadurch schnell ein Lernerfolg einstellt. Ob Sie es glauben oder nicht, in Kürze werden auch Sie ganz natürlich von Variablen, Standardabweichungen oder Konfidenzintervallen sprechen und damit vielleicht auch ihr Umfeld zum Staunen bringen. Los gehts…
1.1 Grundlagen zu Variablen
In diesem Kapitel wollen wir uns zunächst mit der Grundlage der Statistik beschäftigen, den Zahlen. Wenn man viele Zahlen vorliegen hat spricht man von Daten. Dies könnten beispielsweise die Verkaufszahlen unserer Burger-Kette des letzten Jahres sein oder die Ergebnisse einer Mitarbeiterbefragung. Diese Daten beinhalten dann sehr unterschiedliche Arten von Zahlen, sogenannte Variablen. Dies könnte z.B. der Umsatz pro Tag, oder die durchschnittliche Zufriedenheit eines Mitarbeiters sein. Für jede dieser Variablen beinhalten Daten oft viele Werte, z.B. den Umsatz jedes einzelnen Kunden unserer Burger-Filiale im letzten Jahr. Jeder dieser Kunden wird dann Merkmalsträger und sein Umsatz Merkmalsausprägung genannt.
Was sind Variablen?
Beobachtbare oder messbare Merkmale, die verschiedene Werte annehmen können, werden als Variablen bezeichnet. Die möglichen Werte einer Variablen werden auch Merkmalsausprägungen genannt. Bei vielen gemessenen Werten spricht man von Daten.
Beispiele
- Die „Körpergröße“ ist eine Variable. Sie kann für verschiedene Personen unterschiedliche Längen in cm (m / mm / Zoll/ …) aufweisen.
- Andere Variablen: Alter, Intelligenz, Kreativität, Attraktivität, …
Übersicht grundlegender Begriffe
Zusammenfassend kann man sagen, dass Statistik sich mit Daten beschäftigt, oder genauer gesagt mit den Merkmalsausprägungen von Merkmalsträgern auf verschiedenen Variablen. Die Begriffe hier nochmal in der Übersicht:
| Merkmalsträger, Fälle, statistische Einheiten („Zeilen im Datensatz“) | Objekte (meist Personen), an denen interessierende Größen erfasst werden |
| Variablen, Merkmale („Spalten im Datensatz“) |
interessierende Größen |
| Merkmalsausprägungen, Daten („Felder im Datensatz“) |
(gemessener) Wert eines Merkmalsträger hinsichtlich eines Merkmals |
Im folgenden Video werden diese Begriffe nochmal am Beispiel unserer Burger-Kette FiveProfs vorgestellt.
Video 1.1. Grundlagen zu Variablen
Klassifikation von Variablen
Im nächsten Schritt wollen wir uns nun näher den verschiedenen Arten von Variablen widmen. Wie wir schon an den Beispielen gemerkt haben, können Variablen von ganz unterschiedlicher Natur sein: Manche beziehen sich auf reine Zahlenwerte wie Umsatz oder Größe, manche haben eher eine sprachliche Ausprägung, wie die Haarfarbe oder der Name, andere wiederum beziehen sich auf Dinge die nur schwer messbar sind, wie die Zufriedenheit oder der Geschmack. Diese Eigenschaften von Variablen haben wiederum einen großen Einfluss auf die Methoden und Verfahren die wir im Folgenden verwenden können. Daher wollen wir nun zunächst eine Struktur entwickeln mit der wir verschiedene Arten von Variablen zuordnen bzw. klassifizieren können.
Welche Arten von Variablen gibt es?
Grundsätzlich können Variablen klassifiziert werden in:
- Qualitative oder quantitative Variablen
Was misst die Variable? Die Zugehörigkeit zu einer Kategorie oder die Ausprägung auf einem Kontinuum? - Diskrete oder stetige Variablen
Ist die Anzahl der möglichen Werte endlich oder unendlich? - Latente oder manifeste Variablen
Wie können wir die Variable erfassen? Durch direkte Beobachtung oder nur indirekt? - Unabhängige oder abhängige Variablen
Ist die Variable im Versuch die zu messende Variable oder die vermutete Einflussgröße auf die zu messende Variable?
Hierbei können die ersten drei Arten der Klassifikation für jede Variable aufgrund der festen Eigenschaften der Variable vorgenommen werden. Die Frage ob eine Variable abhängig oder unabhängig ist, hängt jedoch vom Forschungsdesign ab. In der Praxis bedeutet das, dass dieselbe Variable in einem Versuch die abhängige Variable und in einem anderen Versuch die unabhängige Variable sein kann. Verwirrt? Keine Sorge, wir widmen uns nun jedem dieser Themen im Detail.
1.2 Qualitative und Quantitative Variablen
Qualitative Variablen (kategorial)
Qualitative Variablen beschreiben die Zugehörigkeit einer Person oder eines Objektes zu einer Kategorie. Üblicherweise haben die Ausprägungen dann auch Buchstaben und keine Zahlen (z.B. „Köln“ als Wohnort). Bei genau zwei Ausprägungen spricht man von einer dichotomen oder binären Variablen (z.B. „Schwanger“ und „Nicht-Schwanger“).
Beispiele
- Lieblingsburger
- Geschlecht
- Wohnort
- Fußballverein
- Haarfarbe
Quantitative Variablen (kontinuierlich, metrisch, skaliert)
Quantitative Variablen beschreiben die Ausprägung eines Merkmals auf einem Kontinuum. Die Ausprägungen sind quantitativ, das heißt alle Werte werden mit Zahlen dargestellt. Sie geben die Ausprägungen einer Größe in einer Form wieder, die auch Aussagen über Abstände zwischen den Ausprägungen erlaubt. Wenn beispielsweise die Größe von Personen mit einem Meterstab gemessen wird, so kann eindeutig festgestellt werden, wer am größten ist und auch um wieviel diese Person größer ist als eine andere Person.
Beispiele
- Gewicht
- Schulnote
- Alter
- Temperatur
- Einkommen
Auch wenn die Begriffe quantitative und qualitative Variable in der Praxis häufig gebraucht werden, so ist ihre Definition nicht umfassend, da es auch Variablen gibt, die in keine der beiden Kategorien passt. Ein Beispiel hierfür sind Ränge beim 100-Meter lauf. Hier können wir zwar sagen wer als erster ins Ziel gegangen ist, aber nicht um wieviel schneller diese Person war als der zweitplatzierte. Auch wird der Begriff der quantitativen Variable oft mit quantitativen Erhebungsverfahren verwechselt. Letzteres beschreiben Methoden wie Fragebogenforschung, die durchaus auch qualitative Fragen beinhalten können (z.B. wenn im Fragebogen nach der Augenfarbe gefragt wird). Daher werden wir im nächsten Kapitel mit den sogenannten Skalenniveaus eine exaktere Klassifizierung von Variablen in dieser Dimension kennen lernen.
Das folgende Video soll Ihnen den Unterschied zwischen quantitativen und qualitativen Variablen nochmal an Beispielen näherbringen.
Video 1.2 Qualitative und Quantitative Variablen
1.3 Diskrete und Stetige Variablen
Bei quantitativen Variablen unterscheidet man zusätzlich noch in diskrete und stetige Variablen. Um den Unterschied zwischen diesen Formen zu verstehen, ist es Hilfreich sich die Frage zu stellen, ob man die zu Grunde liegende Variable zählen kann (diskret) oder messen muss (stetig).
Diskrete Variablen
Die Anzahl der möglichen Werte innerhalb eines beliebigem Intervalls ist endlich und damit genau abzählbar. Hierbei kann man Werte nicht beliebig genauer bestimmen, sondern es gibt feste Einheiten in denen die Merkmalsausprägungen bestimmt werden können (z.B. kann ich nur ganze Menschen in meiner Burgerfiliale zählen).
Beispiele
- Anzahl Kunden in meiner Burgerfiliale
- Augenzahl auf einem Würfel
- Anzahl Parkplätze
- Notenskala
- Alter in Jahren
Stetige Variablen
Die Variable kann innerhalb eines Intervalls auf einem Kontinuum beliebig genau beschrieben werden, d.h. die Anzahl der möglichen Werte ist unendlich. Hierbei kann man also Werte beliebig genau messen, wodurch es praktisch nicht mehr vorkommt, das zwei oder mehr Merkmalsträger die selbe Merkmalsausprägung haben. Denken Sie dabei z.B. an Zeit, die man beliebig genau messen kann (Sekunden, Millisekunden etc.). Sicherlich finden sich in Ihrem Studiengang viele mit dem gleichen Alter in Jahren (diskrete Variable), aber wohl niemand der zur gleichen Millisekunde, wie Sie geboren ist und damit auch wirklich gleich alt ist (Alter als stetige Variable).
Beispiele
- Temperatur
- Körpergröße
- Gewicht
- Zeit bzw. Alter wenn exakt gemessen
Das folgende Video soll Ihnen den Unterschied zwischen stetigen und diskreten Variablen nochmal an Beispielen näherbringen.
Video 1.3. Diskrete und Stetige Variablen
1.4 Manifeste und Latente Variablen
Manifeste Variablen
Bei Manifesten Variablen können direkt beobachtet oder gemessen werden und lassen so keinen Interpretationsspielraum zu. Wenn jemand z.B. 1,78 cm groß ist oder aus Köln kommt, so handelt es sich hierbei um jeweils manifeste Variablen. Beobachtbar bezieht sich dabei jedoch nicht nur auf das mit dem Auge sichtbare (Sie könnten jemand wahrscheinlich nicht ansehen ob er aus Köln kommt). Vielmehr geht es dabei darum ob ein Merkmal eindeutig und objektiv festgelegt ist und damit keiner weiteren Operationalisierung bedarf. So lässt sich die Größe und der Geburtstort z.B. eindeutig aus dem Personalausweis ermitteln, die Vorfreude der Person auf den Karneval (latente Variable) hingegen lässt sich sehr unterschiedlich messen, worauf wir gleich im Folgenden eingehen.
Beispiele für manifeste Variablen
- Gewicht
- Anzahl Burger-Filialen
- Wohnort
- Geschlecht
Latente Variablen (Konstrukte)
Diese Variablen sind nur indirekt zu erfassen. Dies geschieht durch Rückschluss aus anderen manifesten Variablen. Die Auswahl geeigneter manifester Variablen für die Messung eines Konstrukts nennt man Operationalisieren. Das Problem dabei: es gibt für jede latente Variable unterschiedliche manifeste Variablen / Operationalisierungen. Wenn Sie zum Beispiel die Zufriedenheit mit diesem Buch als (latente) Variable messen wollen, so könnten Sie das über eine Befragung (mit sehr unterschiedlichen Fragen), oder auch über die Auswertung der durchschnittlichen Lesezeiten, der Likes in sozialen Medien oder der Bewertungen auf Amazon machen.
Beispiele für latente Variablen
- Zufriedenheit mit unserer Burger-Filiale
- Spaß an der Arbeit
- Intelligenz
- Markenimage
Das folgende Video soll Ihnen den Unterschied zwischen latenten und manifesten Variablen nochmal an Beispielen näherbringen.
1.4 Latente und Manifeste Variablen
1.5 Unabhängige und Abhängige Variablen
Häufig (aber nicht immer) ist es sinnvoll, Variablen als unabhängige oder abhängige Variablen zu klassifizieren. Grundsätzlich werden diese Begriffe vor allem für die hypothesenprüfende Forschung verwendet, zum Beispiel bei der Durchführung von Experimenten. Anders als bei den bisher besprochenen Klassifizierungen, ist diese Einordnung nicht basierend auf der Variable selbst, sondern basierend auf dem jeweiligen Untersuchungskontext und Versuchsaufbau. Ein und dieselbe Variable kann also im einen Experiment eine abhängige und im anderen Experiment eine unabhängige Variable sein.
Unabhängige Variable (Prädiktor)
Die unabhängige Variable (UV) ist diejenige Variable, die im Rahmen eines Experiments variiert wird, um deren Auswirkungen auf die abhängige Variable zu erfassen. Wird sie nicht variiert, sondern nur gemessen, nennt man sie Prädiktor. Die UV ist die vermutete Einflussgröße auf die abhängige Variable (AV).
Abhängige Variable (Kriterium)
Die abhängige Variable (AV) ist diejenige Variable, deren Veränderung im Rahmen eines Experiments infolge des Einflusses der UV gemessen wird. Die AV soll die Wirkung durch die UV erfassen. Die AV heißt deshalb abhängige Variable, weil ihre Ausprägungen zumindest zum Teil von der UV abhängen. Die AV soll sich in Abhängigkeit von der UV verändern. Wird die UV nicht variiert, nennt man die AV auch Kriterium.
Beispiele für abhängige und unabhängige Variablen
Es wird untersucht:
- Der Einfluss der Temperatur im Raum (UV) auf die Konzentrationsfähigkeit der Studierenden (AV).
- Wie beeinflusst die Leistung des Dozenten (UV) die Anwesenheit der Studierenden in der Vorlesung (AV)?
- Die Auswirkung von Homeoffice (UV) auf die Arbeitsmotivation der Mitarbeiter (AV).
Das folgende Video soll Ihnen den Unterschied zwischen UV und AV nochmal an Beispielen näherbringen.
1.5 Unabhänige und Abhängige Variablen
1.6 Variablen messen – Messtheorie
Bei einer Messung wird versucht die Realität – bzw. einen Ausschnitt davon – in Messwerten (Zahlen) abzubilden. Messen ist die Zuordnung von Zahlen zu Merkmalsträgern auf Basis ihrer Merkmalsausprägungen anhand definierter Regeln (z.B. Körpergröße in cm, Reaktionszeit in ms, Schulleistung in Noten, Intelligenz in IQ-Werten). Die Regeln, nach denen Zahlen zu Merkmalsträgern zugeordnet werden, werden in einer Skala definiert. Die möglichen Ausprägungen nennt man auch Skalierung. Hierbei sind die Mindestvoraussetzung:
- Exklusivität: Unterschiedliche Merkmalsausprägungen werden unterschiedlichen Zahlen zugeordnet.
- Exhaustivität: Es existiert eine Zahl für jede beobachtete oder potentiell bestehende Merkmalsausprägung.
Eine umfängliche – und zugegebener Weise komplexe – Definition für das Messen lautet wie folgt:
„Messen ist eine Zuordnung von Zahlen zu Objekten oder Ereignissen, sofern diese Zuordnung eine homomorphe Abbildung eines empirischen Relativs in ein numerisches Relativ ist.“[1]
Eine homomorphe Abbildung ist hierbei eine nicht umkehrbare eindeutige Abbildung von dem was man sieht oder beobachtet (empirisches Relativ) in eine Zahl (numerisches Relativ). Homomorph bedeutet, dass die Relationen der Zahlen im numerischen Relativ eindeutig den Relationen der Objekte im empirischen Relativ entsprechen. Ist Peter also zum Beispiel sichtbar größer als Jana, so sollte Peter auch eine größere Zahl bekommen als Jana. Wie die Skala konkret aussieht, hierfür gibt es theoretisch sehr viele Möglichkeiten. Um die vorher genannten Bedingungen zu erfüllen, würde es Beispielsweise reichen für Peter die Zahl 2 und für Jana die Zahl 1 zu vergeben. Üblicherweise würden wir hier jedoch sicherlich in Metern oder Zentimetern messen, in den USA jedoch in Foot und Inch. Bei der Entwicklung von messbaren Skalen gilt es daher grundsätzlich folgende Aspekte zu beachten:
- Repräsentationsproblem: die Repräsentation empirischer Objektrelationen durch Relationen der Zahlen, die den Objekten zugeordnet werden (z.B. Hans < Otto; 1 < 2)
- Eindeutigkeitsproblem: die Eindeutigkeit der Zuordnungsregeln ( z.B. Addition einer Zahl zu der Skala; cm -> mm )
- Bedeutsamkeitsproblem: die Bedeutsamkeit der mit Messvorgängen verbundenen numerischen Aussagen ( z.B. können sinnvolle Mittelwerte gebildet werden?)
Auf den ersten Blick scheint die Lösung dieser drei Probleme der sehr komplex (ist sie auch, vor allem wenn die Logik als Wissenschaft eingeschaltet wird). Für die Lösung dieser Probleme hat Stevens (1946) das Konzept der vier Skalenniveaus entwickelt, welches bis heute in allen gängigen Methoden- und Statistiklehrbüchern, sowie in den gängigen Statistikprogrammen verwendet wird. Stevens unterscheidet hierbei vier Skalenniveaus: Nominal-, Ordinal-, Intervall- und Ratioskala, die wir uns im Folgenden näher ansehen wollen.
Eine kurze Einführung zur Messtheorie und den Skalenniveaus gibt es in folgendem Video:
1.6 Variablen messen – Messtheorie
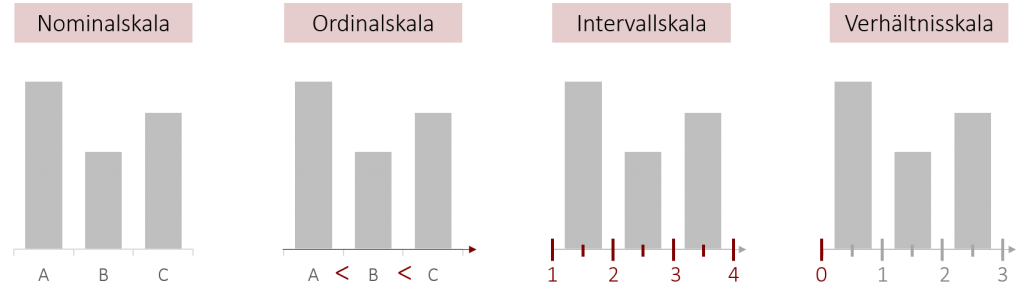
1.7 Variablen – Skalenniveaus
In den Sozialwissenschaften wird zwischen folgenden vier Skalenniveaus unterschieden:
- Nominalskala
- Ordinalskala
- Intervallskala
- Verhältnisskala
In der Praxis (und in den meisten Statistikprogrammen) wird jedoch meist das Intervallskalenniveau und Verhältnisskalenniveau zusammengefasst und als „metrisch“ oder parametrisch“ bezeichnet, da der Unterschied zwischen diesen beiden Kategorien eher von theoretischem als praktischem Interesse ist. Lassen Sie uns nun die Skalenniveaus im Detail betrachten.
Nominalskala
Objekte mit gleicher Merkmalsausprägung erhalten gleiche Zahlen, Objekte mit verschiedener Merkmalsausprägung erhalten verschiedene Zahlen.
- Interpretation: Gleich/ungleich, d.h. Vergleich der Merkmalsausprägungen zweier Objekte beschränkt sich auf die Frage, ob die beiden Merkmalsausprägungen übereinstimmen oder nicht
- Definierte Relationen: =/≠
Anders ausgedrückt, sagen die Zahlen in diesem Fall nur aus, ob ein Merkmalsträger die gleiche Eigenschaft hat (z.B. die gleiche Haarfarbe oder Wohnort) oder eine andere. Die Variable lässt hierbei jedoch keine Bewertung zu, man kann also nicht sagen „Blond > Rothaarig“ oder „Köln < Stuttgart“ sondern nur gleich oder ungleich (= oder ≠ ).
Beispiele
- Bundesländer
- Rückennummern einer Sportmannschaft
- Geschlecht: Allen weiblichen Personen wird eine 1 zugeordnet, allen männlichen eine 2 (oder weiblich=0 | männlich=1)
- Gruppenzugehörigkeit: Abteilung 1 = 1, Abteilung 2 = 2 (oder anders herum möglich)
Ordinalskala (Rangskala)
Eine Ordinalskala ordnet Objekten Zahlen zu, die so festgelegt sind, dass von jeweils zwei Objekten das Objekt mit der größeren Merkmalsausprägung die größere Zahl erhält (oder auch anders herum). Während dadurch klar ist welche Merkmalsausprägung größer ist, erlauben die Zahlen jedoch keine Aussagen zu den Abständen zwischen den werten (also wieviel größer ein wert ist).
- Interpretation: Gleich/ungleich, größer/kleiner, d.h. eine Rangfolge zwischen den Merkmalsausprägungen kann gebildet werden
- Definierte Relationen: =/≠; > <
Anders ausgedrückt, könnte man also nun sagen das es eine klare Rangfolge gibt, z.B. Master>Bachelor>Abitur, jedoch über die Abstände der einzelnen Ausprägungen keine Aussage getroffen werden kann (Ein Master ist z.B. nicht doppelt so viel wie ein Bachelor).
Beispiele
- Reihenfolge meiner 3 Lieblings-Burgerketten
- Rangfolge der Läufer beim 100-Meter Lauf
- Rankings (z.B. Hochschulrankings)
- Streng genommen auch alle Einschätzungsskalen
(trifft zu = 4, trifft eher zu =3, trifft eher nicht zu =2, trifft nicht zu = 1)
Hinweis: In der Praxis werden die meisten Einschätzungsskalen (Beispielsweise sogenannte Likert-Skalen in Fragebögen von 1-5) im Rahmen einer sogenannten „per fiat“-Messung (Messung durch Vertrauen) als intervallskaliert betrachtet, da sonst viele statistischen Verfahren gar nicht angewendet werden können.
Intervallskala
Eine Intervallskala gibt zusätzlich zur Ordnung der Merkmalsausprägungen auch Auskunft über die Abstände zwischen den Ausprägungen. Gleich große Zahlendifferenzen (bzw. Intervalle) stehen für gleich große Unterschiede der Merkmalsausprägungen (= Äquidistanz).
Hat z.B. ein Objekt den Skalenwert 1, so ist es von dem Objekt mit dem Skalenwert 2 genauso weit entfernt, wie dieses von einem Objekt mit dem Skalenwert 3. Der Nullpunkt (und auch die Einheit) einer Intervallskala sind jedoch willkürlich.
- Interpretation: Gleich/ungleich, größer/kleiner, Gleichheit von Differenzen. Aber: es können keine Aussagen über das Verhältnis gebildet werden
- Relationen und Operationen: =/≠; > <; /- (Operationen heißt, ich darf Differenzen zwischen Daten rechnen bzw. Daten addieren)
Beispiele
- Temperatur in Celsius oder Fahrenheit
- Intelligenzquotient oder Mitarbeiterzufriedenheit
Verhältnisskala
Eine Verhältnisskala ist eine Intervallskala mit absolutem Nullpunkt (= Anfangspunkt der Skala), der das „Nichtvorhandensein“ des Merkmals ausdrückt. Dies ist bei den meisten messbaren Größen, wie Gewicht, Größe oder Alter, der Fall.
- Interpretation: Gleich/ungleich, größer/kleiner, Gleichheit von Differenzen und Verhältnissen
- Relationen und Operationen: =/≠; > <; +/-; ×/:
(hier darf ich Daten zusätzlich miteinander Multiplizieren / Dividieren und Verhältnisse bilden)
Tipp: Bei einer Verhältnisskala ist die Aussage 4 ist doppelt so viel wie 2 inhaltlich richtig, bei einer Intervallskala nicht. So sind z.B. 30 Grad Celsius nicht doppelt so warm wie 15 Grad Celsius (auch wenn viele das umgangssprachlich behaupten). Hingegen sind 500 Grad auf der Kelvin-Skala tatsächlich doppelt so warm, wie 250 Grad Kelvin, da hier ein natürlich Nullpunkt (0 Kelvin) vorliegt.
Beispiele
- Größe in m, cm, mm, km, …
- Gewicht in kg, g, mg, …
- Zeit in sec, min, h, …
- Einkommen in Euro, Cent, $, …
- Temperatur in Kelvin
Skalenniveaus & Statistik
Für die Statistik (zulässige Darstellungen, Berechnungen und Tests) ist es relevant, ob Merkmale nominal-, ordinal- oder (mindestens) intervall-skaliert sind. Die Unterschiede zwischen Intervall- und Verhältnisskala sind für die Statistik irrelevant und für die Anwendung nur von nachrangigem Interesse (Allerdings ist die Unterscheidung relevant, wenn man Verhältnisse bilden will). Daher verwenden alle Statistikprogramme und auch einige Fachbücher nur diese drei Skalenniveaus.
Tipp: Wenn sich bei der Operationalisierung, z.B. eines latenten Konstrukts, mehrere Skalenarten anbieten, sollte diejenige mit dem höchsten Skalenniveau gewählt werden. Dieses kann später auch immer in ein niedrigeres umgewandelt werden.
Noch nicht ganz klar? Das folgende Video zeigt nochmal das Thema Skalenniveaus am Beispiel unserer Burger-Kette Five-Profs.
1.8 Variablentypen in der Übersicht
Die folgende Tabelle fasst nochmal die Skalenniveaus und die wichtigsten Eigenschaften zusammen knapp zusammen:
| Skalenniveau | Beispiele | Mögliche Aussagen |
| Nominalskala | Geschlecht, Diagnosen | Gleichheit/ Verschiedenheit |
| Ordinalskala | Schulbildung, Ratings | Größer / Kleiner Relation |
| Intervallskala | IQ, Persönlichkeits-merkmale | Gleichheit von Differenzen |
| Verhältnisskala | Gewicht, Einkommen | Gleichheit der Verhältnisse |
Das wissen um das richtige Skalenniveau wird für Sie im weiteren Verlauf noch sehr wichtig sein, da fast alle statistischen Verfahren ein gewisses Skalenniveau voraussetzen. Um diese, auch in aktueller Statistik-Software, rechnen zu können, müssen Sie also sicher im Umgang mit diesen Begriffen werden. Zum Abschluss dieses Kapitels wird die Übersicht der Skalenniveaus im folgenden Video nochmal wiederholt und vertieft:
1.8 Variablentypen in der Übersicht
1.9 Variablen in SPSS eingeben
SPSS bietet zwei Sichtweisen auf Ihre Datensatz, die Datenansicht und die Variablenansicht. In diesem Kapitel wollen wir uns zunächst damit beschäftigen wie neue Variablen in SPSS angelegt werden können. Beispielsweise ist dies dann der Fall, wenn Sie einen Papierfragebogen verwendet haben und nun die Daten in SPSS eingeben wollen. Der erste Schritt vor der Dateneingabe ist, dass Sie die Variablen in SPSS anlegen. Dazu müssen Sie in die Variablenansicht wechseln und dort zunächst in der Spalte Name einen Variablennamen festlegen. Dabei gibt es einige Regeln zu beachten. Hier die wichtigsten Regeln:
- Sinnvolle Namen mit Bezug zur Erhebung bzw. zum Fragebogen wählen, z.B. sollte die Fragennummer auftauchen
- Der Name darf max. 64 Zeichen lang sein – idealerweise kurze Namen wählen, da dies übersichtlicher ist.
- Längere Bezeichnungen können später bei der Variablenbeschriftung noch vergeben werden
- Variablenname muss eindeutig sein
- Variablenname muss mit einem Buchstaben (oder @) beginnen
- Der Variablenname darf kein Leerzeichen enthalten
- Bestimmte Symbole dürfen nicht verwendet werden, z.B. +, -, $, &
- Groß- und Kleinschreibung wird gleichbehandelt.
Die nächste Spalte ist der Typ (Variablentyp). Grundsätzlich unterscheidet man beim Variablentyp zwischen Numerisch für Zahlen und Zeichenfolge für Variablen die Text beinhalten. Letztere müssen für weitere Analyse umcodiert werden, d.h. die Antworten in Zahlen „übersetzt“ werden, deren Bedeutung unter Wertelabels definiert werden müssen. Die weiteren Auswahlmöglichkeiten werden in der Praxis sehr selten genutzt und daher an dieser Stelle nicht besprochen. Die Breite legt fest, wie viele Zeichen maximal in die Variable eingegeben werden können. Vor allem bei Text-Variablen aus offenen Fragen sollte dieses Feld groß genug gewählt werden da sonst beim Import von Daten Text abgeschnitten werden kann. Die Dezimalstellen legen fest wie viele Nachkommastelen die Variable haben soll. Die Breite muss so groß sein, dass alle Dezimalstellen angezeigt werden können. Mit Beschriftungen können einer Variable weitere Beschreibungen zugeordnet werden um diese weiter zu erklären oder um zum Beispiel die Frage aus einem Fragebogen zu dokumentieren.
Das folgende Video zeigt die Definition von Variablen an einigen Beispielen.
Video 1.9 Variablen in SPSS eingeben
1.10 Übungsfragen
Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!
In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!
1.11 Übungsaufgaben
- Orth, Bernhard (1983): Grundlagen des Messens. In: Feger, H. et al. (Hg.): Messen und Testen. Göttingen. S.136-180. ↵



