Inferenzstatistik
8 Parameterschätzung
8.0 Einführung
Im vorausgegangenen Kapitel haben wir gelernt wie man eine Stichprobe zieht. Stichproben werden immer dann gezogen wenn es unmöglich oder zumindest nicht wirtschaftlich wäre Daten von allen Personen der Population zu erheben. Dabei sollte man nicht vergessen, dass die Population sich nicht auf alle Menschen bezieht sondern immer durch das Studienziel bestimmt wird. Die Population könnten also z.B. alle BWL-Studenten über 20 sein oder alle Kunden unserer Burger-Filiale. In der deskriptiven Statistik sind Kennwerte exakt bestimmbar. Wir können z.B. das exakte Durchschnittsalter unserer Mitarbeiter aus der Mitarbeiterdatenbank berechnen. Die „Kennwerte“ einer deutlich größeren Population können wir jedoch nur indirekt, durch das ziehen einer Stichprobe, bestimmen. Diese „Kennwerte einer Population“ werden Parameter genannt und werden auf Basis einer gezogenen Stichprobe geschätzt. Deswegen beschäftigen wir uns in diesem Kapitel auch mit der Schätzung von Populationsparametern. Beispielsweise könnte das Ziel dabei sein, eine möglichst genaue Schätzung für das Durchschnittsalter unserer Kunden zu bekommen. Das exakte Durchschnittsalter unserer Kunden werden wir jedoch niemals ermitteln können, da sicherlich nicht alle unsere Burger-Kunden uns ihr Alter verraten werden und es auch äußerst unhöflich wäre jeden Kunden danach zu fragen.
In diesem und dem nächsten Kapitel widmen wir uns also nun der Schätzung von Populationsparametern. Um Populationsparameter aus den entsprechenden Stichprobenkennwerten zu schätzen, gibt es in der Inferenzstatistik zwei Schätzverfahren:
- die Punktschätzung
- die Intervallschätzung.
Der wesentliche Unterschied zwischen den beiden Verfahren ist, dass die Punktschätzung einen möglichst genauen Näherungswert für den gesuchten Populationsparameter angibt, während die Intervallschätzung stattdessen einen Bereich angibt, in dem der gesuchte Parameter mit einer bestimmten Wahrscheinlichkeit liegt. Bei der Punktschätzung werden Eigenschaften über die Population als exakter Wert ermittelt (z.B. die Zahlungsbereitschaft beträgt 1.500€) und meist mit einem Maß für den Schätzfehler versehen. Bei der Intervallschätzung wird ein Intervall für die Eigenschaft der Population angegeben (z.B. die Zahlungsbereitschaft liegt zwischen 1.400 und 1.600€) und diese dann mit einer Wahrscheinlichkeit versehen (z.B. 95%). Im Folgenden wollen wir uns nun also zunächst mit der Punktschätzung beschäftigen. Hierfür fangen wir zunächst mit den Basics an: Kennwerte und Parameter.
Einen guten Überblick über das Thema „Schätzung von Populationsparametern“ bietet Ihnen zudem das folgende Video von Five Profs.
8.1 Parameterschätzung | Einführung
8.1 Kennwerte und Parameter
Kennwerte
Kennwerte haben Sie bereits im ersten Kapitel kennengelernt. Sie beziehen sich in der Inferenzstatistik immer auf die Stichprobe und werden mit lateinischen Buchstaben notiert.
Beispiele für Kennwerte in der Inferenzstatistik:
| Mittelwert der Stichprobe | |
| Standardabweichung der Stichprobe | s |
Diese Stichprobenkennwerte werden in der Inferenzstatistik als Zufallsvariablen aufgefasst. Dies ist so, weil die Kennwerte vom Zufall – nämlich von der zufällig gezogenen Stichprobe – abhängen. Je nach Ziehung erhalten wir so beispielweise mal einen höheren oder niedrigeren Mittelwert für die Zahlungsbereitschaft.
Das Gute daran: Die Stichprobenkennwerte schwanken zwar zufällig, aber immerhin um den „wahren Wert“ der Population herum (bis auf die Streuungsmaße, aber dazu später mehr). Diese Tatsache hilft uns später, um die gesuchten Größen der Population schätzen zu können.
Parameter
Um die Werte der Population besser von den Kennwerten der Stichprobe abgrenzen zu können, hat man ihnen einen anderen Namen gegeben. Man bezeichnet die (in der Regel) unbekannten „Kennwerte“ der Population als Populationsparameter und notiert sie zur besseren Unterscheidung mit griechischen Buchstaben. Parameter sind im Gegensatz zu Stichprobenkennwerten feste Werte von Populationsverteilungen. Dies ist so, weil sich Parameter immer auf dieselbe zugrundeliegende Menge – auf die Population – beziehen. Solange sie sich nicht verändert, verändern sich auch ihre Parameter nicht und bilden somit feste Werte. Eben diese Parameter möchten wir in der Parameterschätzung mittels unserer Stichprobenkennwerte schätzen. Beispielsweise hat unsere Stichprobe von 100 Kunden für die Zahlungsbereitschaft den Kennwert 5€ ergeben. Diesen nutzen wir als Schätzer für den (unbekannten) Populationsparameter, der die Zahlungsbereitschaft aller unserer Kunden darstellt. Da wir ja nicht alle unsere Kunden nach der Zahlungsbereitschaft befragen können, wird dieser Populationsparameter auch immer unbekannt bleiben und wir müssen uns mit einer Schätzung zufriedengeben. Genau das macht die Inferenzstatistik so knifflig.
Beispiele für Populationsparameter:
| Mittelwert der Population | µ (mi) |
| Standardabweichung der Population | σ (sigma) |
Übersicht
Stichprobenkennwerte und Populationsparameter gehören immer paarweise zusammen. Der Unterschied zwischen ihnen ist die Menge der Merkmalsträger, auf die sie sich beziehen. Stichprobenkennwerte beziehen sich (wie der Name schon sagt) auf eine Stichprobe. Populationsparameter beschreiben hingegen die zugrundeliegende Grundgesamtheit (also alle Menschen oder Untersuchungseinheiten, die wir betrachten). Die nachfolgende Tabelle gibt Ihnen einen Überblick über die gängigsten Stichprobenkennwerte und die dazugehörigen Populationsparameter:
| Kennwert | Parameter | |
| Anteilswert | h bzw. p | π (pi) |
| Mittelwert | µ (mi) | |
| Varianz | s2 | σ2 (sigma quadrat) |
| Standardabweichung | s | σ (sigma) |
| Korrelation | r | ρ (rho) |
8.2 Parameterschätzung | Kennwerte und Parameter
8.2 Punktschätzung
Die Punktschätzung schätzt auf Basis eines Stichprobenkennwerts einen möglichst genauen Näherungswert für den unbekannten bzw. gesuchten Parameter einer Population. Das Ziel des Verfahrens ist es somit einen Punkt zu bestimmen, an dem der gesuchte Parameter mit der höchsten Wahrscheinlichkeit liegt.
Um eine Punktschätzung für einen unbekannten Parameter durchzuführen, ziehen wir zunächst eine Zufallsstichprobe aus unserer Population und bestimmen daraufhin die relevanten Stichprobenkennwerte. Wenn wir beispielsweise den Mittelwert der Zahlungsbereitschaft für alle Kunden (Population) schätzen möchten, bestimmen wir zunächst den entsprechenden Mittelwert der gezogenen Stichprobe. Dieser Stichprobenkennwert ist im Normalfall unser Punktschätzer für den unbekannten Populationsparameter. Ziehen wir z.B. einen Stichprobenmittelwert von = 1.500€, so ist dies unsere Punktschätzung für den unbekannten Populationsmittelwert µ. In diesem Fall schätzen wir, dass der unbekannte Populationsmittelwert µ bei 1.500€ liegt.
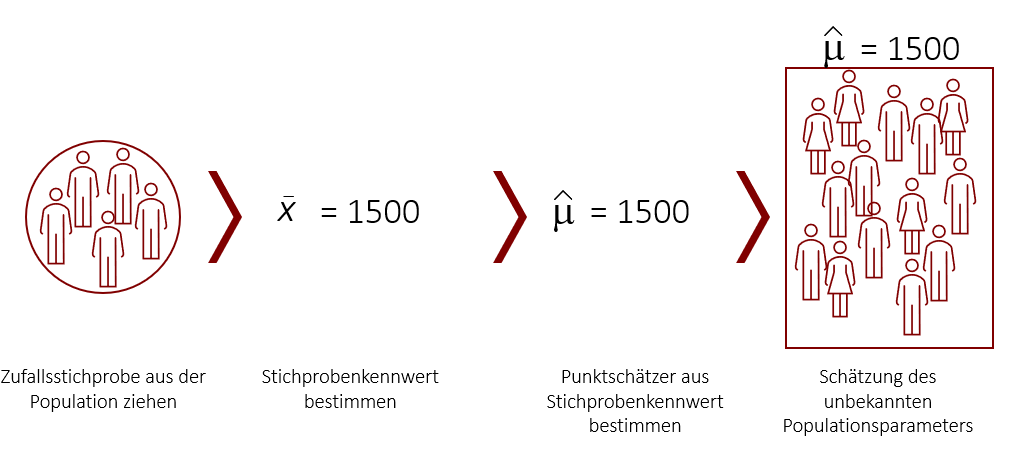
Ein weiteres Beispiel:
Wir möchten den Anteil von Katzenliebhabern in der Population bestimmen. Hierzu ziehen wir eine repräsentative Zufallsstichprobe von 100 Personen und befragen sie anschließend. Wir erfahren, dass 26% unserer Befragten Katzenliebhaber sind. Dieser erhobene Anteilswert von 26% ist unser Punktschätzer für den unbekannten Anteilswert an Katzenliebhabern in der Population.
Auf Basis unserer Stichprobe können wir nun sagen, dass der Anteil an Katzenliebhabern in der Population schätzungsweise bei 26% liegt. Zusätzlich sollten wir noch ein Maß für die Güte dieser Schätzung mit angeben. Hiermit werden wir uns im Folgenden beschäftigen.
Wir können jedoch nicht alle Stichprobenkennwerte einfach als Punktschätzer auf die Population übertragen. Dafür müssen die Stichprobenkennwerte erwartungstreu sein. Was sich genau hinter diesem Begriff verbirgt, erfahren Sie in den nächsten Abschnitten.
Ein weiteres Problem bei dieser Vorgehensweise besteht darin, dass wir nicht davon ausgehen können, dass der Punktschätzer den gesuchten Populationsparameter auch tatsächlich trifft. Dieser Fall wäre sogar sehr unwahrscheinlich, da die Punktschätzung auf Kennzahlen beruht, die je nach Zufallsstichprobe mal höher oder niedriger ausfallen können. Um dem entgegenzuwirken, lohnt es sich, die Genauigkeit der Punktschätzung zu ermitteln und mit anzugeben. Ein geeignetes Maß dafür ist der Standardfehler des Schätzers.
Bevor wir uns jedoch mit der Erwartungstreue und anderen Gütekriterien der Schätzer befassen, werfen wir einen Blick auf die sogenannten „Stichprobenkennwerteverteilungen“. Sie bilden die Basis für die eben genannten Begriffe und sind deshalb für das Verständnis unerlässlich.
8.3 Stichprobenkennwerteverteilung
Die Stichprobenkennwerteverteilung ist eine hypothetische Verteilung. Sie bildet zwar die Basis für statistische Theorien, existiert jedoch in der Realität nicht – höchstens in Simulationen. Deshalb lassen Sie uns gemeinsam in ein Gedankenexperiment abtauchen, um die Stichprobenkennwerteverteilung näher zu verstehen.
Beispielweise wollen Sie bestimmen, wieviel Euro Personen pro Monat in Frankreich für Fastfood ausgeben. Aus diesem Anlass ziehen Sie nacheinander aus der Population der französischen Staatsbürger Zufallsstichproben mit immer derselben Größe n. Hierbei ziehen sie jedoch nicht nur eine oder zwei Stichproben, sondern sehr, sehr viele gleichgroße Zufallsstichproben. Für jede Stichprobe berechnen Sie daraufhin den Mittelwert der Ausgaben für Fastfood pro Monat. So erhalten Sie sehr viele Mittelwerte, die sich von Stichprobe zu Stichprobe leicht unterscheiden (je nachdem wie viele Fastfood-Fans Sie zufällig in der Stichprobe haben). Wenn Sie nun alle Mittelwerte in eine Liste schreiben und der Größe nach ordnen entsteht eine neue Verteilung – die Verteilung der Stichproben-Mittelwerte oder anders gesagt die Stichprobenkennwerteverteilung. Dasselbe können Sie auch mit den anderen Kennwerten machen und erhalten dadurch beispielweise eine Stichprobenkennwerteverteilung der Standardabweichungen.
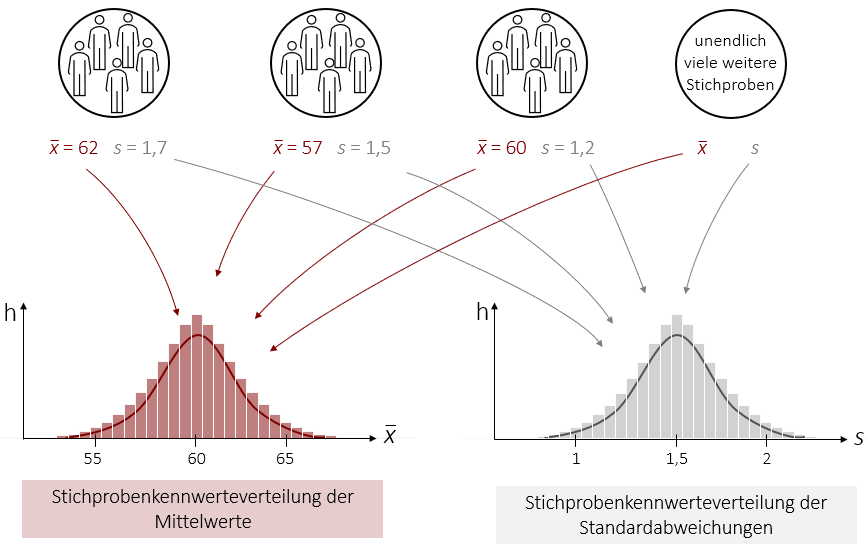
Um das eben gesagte in einen Satz zu bringen: Als Stichprobenkennwerteverteilung wird die Verteilung aller möglichen Ausprägungen eines Stichprobenkennwertes bezeichnet, die entsteht, wenn man nacheinander (unendlich viele) Stichproben der gleichen Größe aus einer Population zieht.
Die Verteilung der Stichprobenkennwerte sieht dabei keinesfalls immer gleich aus. Ihre Form variiert und hängt von verschiedenen Faktoren ab. Diese sind:
- Größe der Stichproben
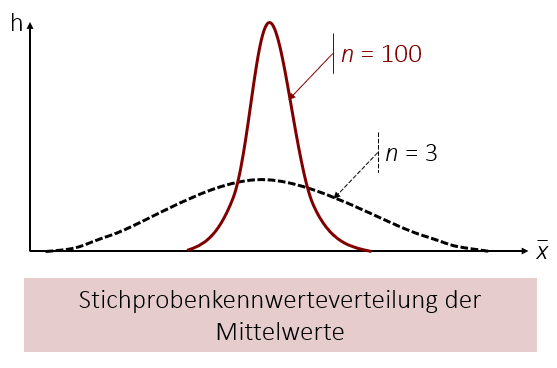
Stellen Sie sich beispielsweise vor, dass Sie eine Stichprobenkennwerteverteilung der Mittelwerte haben. Jeder Mittelwert stammt aus einer Stichprobe mit 3 Personen. Die Mittelwerte dieser kleinen Stichproben können leicht „extreme“ Werte annehmen, da Ausreißer einen hohen Einfluss auf die einzelnen Mittelwerte der Stichproben ausüben. Dadurch hat die Stichprobenkennwerteverteilung eine breite Streuung.
Wenn wir jedoch Mittelwerte aus Stichproben mit jeweils 100 Personen nehmen, ist es deutlich unwahrscheinlicher, dass deren Mittelwerte „extrem“ ausfallen, da sich die Werte in den Stichproben gegenseitig ausmitteln. Für unsere Stichprobenkennwerteverteilung bedeutet dies, dass sie in diesem Fall eine deutlich geringere Streuung aufweist, da die meisten Mittelwerte moderat ausfallen.
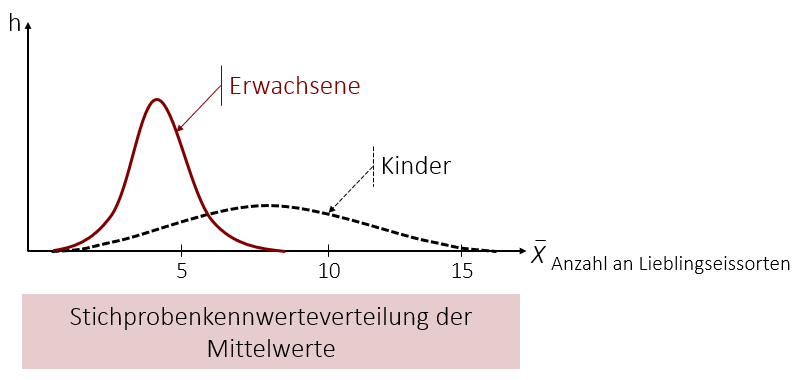
- Verteilung des Merkmals in der Population (Streuung)
Streut das Merkmal in der Population sehr breit, so ist auch die Stichprobenkennwerteverteilung eher flacher und breiter als bei Merkmalen, die in der Population wenig streuen. Schauen wir uns beispielsweise die Stichprobekennwerteverteilungen von Kindern (bis 14 Jahre) und „Erwachsenen“ (ab 14 Jahre) in Bezug auf Lieblingseissorten an. Nehmen wir an, die „Erwachsenen“ haben grundsätzlich eine geringe Anzahl an Lieblingseissorten. Die Mittelwerte der Stichproben würden sich hauptsächlich im Bereich zwischen 3 – 5 Eissorten bewegen. Bei den Kindern hingegen sieht das ganz anders aus. Eine große Anzahl an Kindern hat relativ viele Lieblingseissorten, jedoch gibt es auch viele Kinder, die nur wenige Eissorten mögen. Dementsprechend streuen auch die Mittelwerte der Stichproben bei den Kindern viel stärker. Einige Stichproben liegen bei = 5 Eissorten und andere bei = 12 Eissorten. Das wirkt sich auch auf die Stichprobenkennwerteverteilung aus, die bei den Kindern aufgrund der größeren Streuung der Mittelwerte deutlich flacher verläuft.
- Typ des Kennwerts (Mittelwert, Varianz, Korrelation, etc.)
Je nach Typ des Kennwerts erhalten wir ebenfalls eine andere Stichprobenkennwerteverteilung. Dies bedeutet aber auch, dass wir für verschiedene Kennwerte auch verschiedene Berechnungsformeln brauchen, wenn wir beispielsweise die Varianz der einzelnen Stichprobenkennwerteverteilungen ausrechnen möchten. - Art der Stichprobe
Hiermit ist die Art, wie die Stichproben gezogen wurden, gemeint. Wir gehen immer von Zufallsstichproben aus. Wenn Sie jedoch keine Zufallsstichproben darstellen, so dürften strenggenommen keine Rückschlüsse auf die Population erfolgen (siehe Kapitel „Stichproben“).
Zum besseren Verständnis zeigt Ihnen das folgende Video die Thematik noch einmal anhand eines Beispiels.
8.4 Parameterschätzung | Stichprobenkennwerteverteilung
8.4 Erwartungstreue von Schätzern
Kommen wir nun wieder zurück zu der Punktschätzung. Bei der Punktschätzung benutzen wir einen Stichprobenkennwert, um den entsprechenden unbekannten Populationsparameter zu schätzen. Damit wir jedoch einen Stichprobenkennwert benutzten können, muss dieser erwartungstreu, beziehungsweise unverzerrt sein. Erwartungstreue bedeutet, dass der Schätzer (in diesem Fall der Stichprobenkennwert) bei seiner Schätzung keinem systematischen Fehler unterliegt und so beispielsweise den gesuchten Populationsparameter grundsätzlich zu hoch oder zu niedrig schätzt. Gleichzeitig bedeutet dies nicht, dass der Stichprobenkennwert auch automatisch den richtigen Wert für den gesuchten Populationsparameter trifft. Da eine Stichprobe und damit auch die Stichprobenkennwerte dem Zufall unterliegen, wäre eine richtige Schätzung sogar sehr unwahrscheinlich. Jedoch können wir bei einem erwartungstreuen Schätzer davon ausgehen, dass er den unbekannten Parameter im Mittel richtig schätzt. Doch was bedeutet „im Mittel“ in diesem Fall eigentlich? Schauen wir uns hierzu die Erwartungstreue von Schätzern nochmal genauer anhand der Stichprobenkennwerteverteilung an. Nehmen wir beispielsweise an, dass wir zwei Parameter einer Population schätzen wollen – den Mittelwert und die Varianz. Deren wahren Werte sind µ = 1500 und σ2 = 100, was wir natürlich in der Praxis üblicherweise nicht wissen.

Nun ziehen wir, um die unbekannten Populationsparameter zu schätzen, (theoretisch) unendlich viele Stichproben mit N=5 und erhalten damit unendlich viele Kennwerte. Um nun die Stichprobenkennwerteverteilungen zu erhalten, nehmen wir all unsere Mittelwerte und Varianzen der Stichproben und bilden diese graphisch ab. So erhalten wir zwei Stichprobenkennwerteverteilungen – eine für die Mittelwerte und eine für die Varianzen.
Schauen wir uns zunächst die Stichprobenkennwerteverteilung der Mittelwerte an:
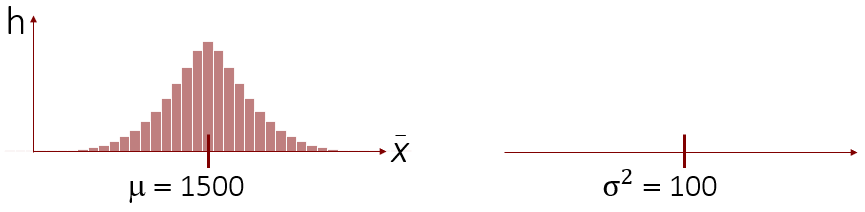
Wir sehen, dass viele Stichprobenmittelwerte höher und viele wiederum niedriger als der wahre Populationsmittelwert ausgefallen sind. Bilden wir jedoch einen Mittelwert über all unsere Stichprobenmittelwerte hinweg (sozusagen den Mittelwert der Mittelwerte), so sehen wir, dass dieser bei 1500 liegt und damit dem unbekannten Populationsparameter µ exakt entspricht. Man kann also sagen, dass der Stichprobenmittelwert den unbekannten Parameter µ durchschnittlich richtig schätzt.
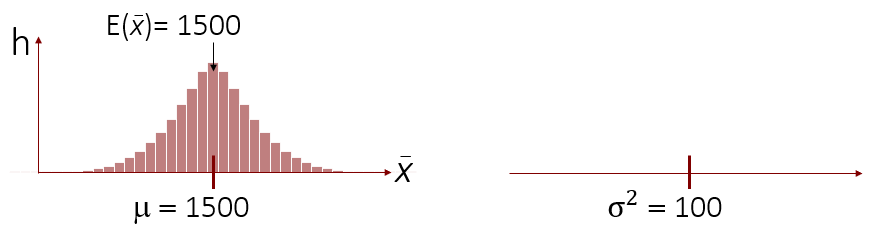
Genau dies bedeutet Erwartungstreue. Wenn der Mittelwert der Stichprobenkennwerteverteilung, der auch als Erwartungswert E() bezeichnet wird, dem Populationsparameter entspricht, so ist er ein erwartungstreuer Schätzer vom Parameter. Damit ist der Mittelwert ein erwartungstreuer Schätzer für µ. Statistisch wird dieser Sachverhalt wie folgt abgebildet:
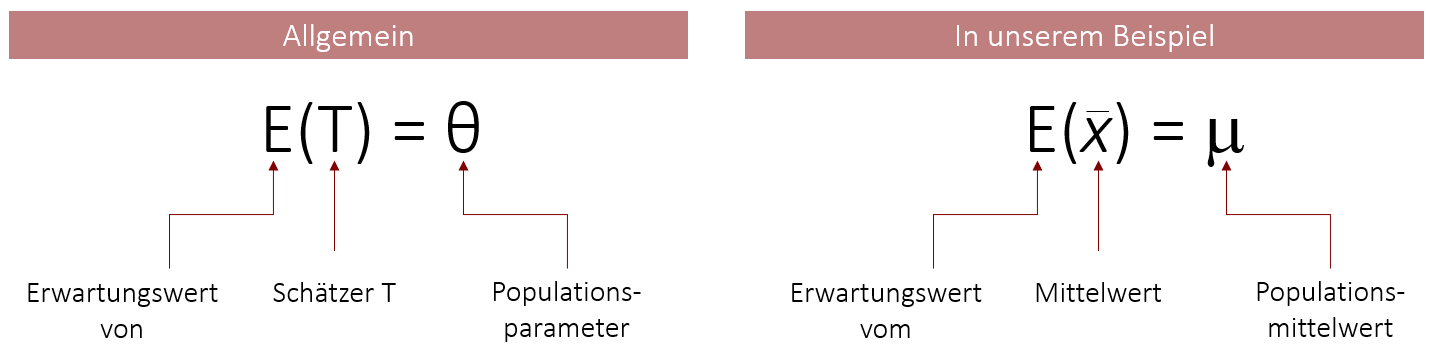
Doch wie sieht es mit der Varianz aus? Ist sie auch ein erwartungstreuer Schätzer für die Populationsvarianz? Schauen wir uns hierfür die Stichprobenkennwerteverteilung der Varianzen (rechts im Bild) an.
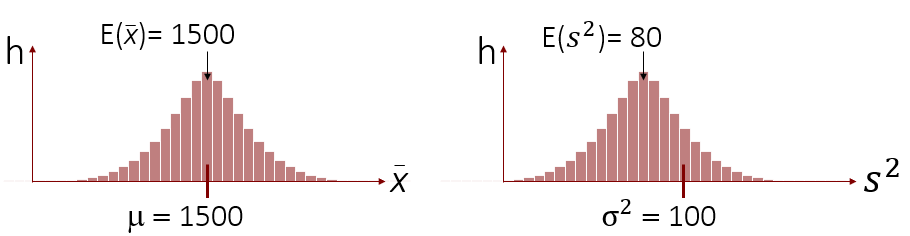
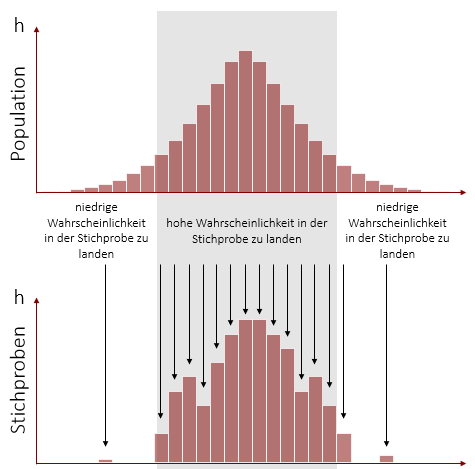
Man sieht bereits auf den ersten Blick, dass die Varianzen in den gezogenen Stichproben zum größten Teil geringer sind als die wahre Populationsvarianz. Würden wir also die Stichprobenvarianz als Punktschätzer für die wahre Varianz benutzen, so wäre es sehr wahrscheinlich, dass wir die wahre Populationsvarianz unterschätzen. Aus diesem Grund ist die Stichprobenvarianz kein erwartungstreuer Schätzer für die Populationsvarianz. Dies können wir auch rechnerisch überprüfen, indem wir den Erwartungswert ablesen und ihn mit der tatsächlichen Populationsvarianz vergleichen. Da E(s2) gleich 80 und damit nicht gleich σ2 = 100 ist, liegt keine Erwartungstreue vor.
Doch warum ist die Varianz in den Stichproben systematisch kleiner als in der Population?
Die Population beinhaltet alle Merkmalsträger – auch die extrem unwahrscheinlichen. In Stichproben hingegen tauchen „extreme“ Merkmalsträger nur selten auf. Viel häufiger beinhalten Stichproben nur die wahrscheinlicheren Fälle. Dadurch schwindet die Varianz in den Stichproben und ist somit kleiner als in der Population. Solch eine systematische Abweichungen wird auch Bias genannt.
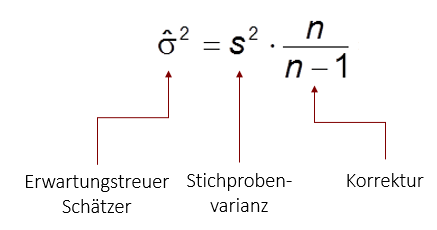
Um die Stichprobenvarianz trotzdem als Punktschätzer für die wahre Populationsvarianz benutzen zu können, müssen wir sie korrigieren. Unser erwartungstreuer Schätzer ist dementsprechend nicht der Stichprobenkennwert s2 selbst (wie beim Mittelwert weiter oben), sondern eine korrigierte Version von ihm. Die Korrektur sieht wie folgt aus:
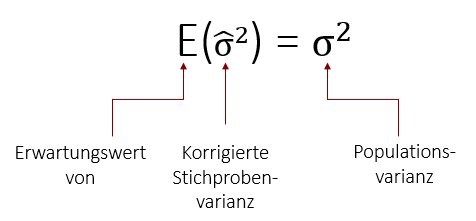
Das Dach über dem Sigma zeigt an, dass es sich um den Schätzer eines Parameters handelt. Dieser ist nun erwartungstreu und kann als Punktschätzer für die Populationsvarianz verwendet werden. Es gilt:
Hinweis: In vielen Texten und Statistikprogrammen wird s2 immer als die korrigierte, also erwartungstreue Varianzschätzung berechnet (z.B. SPSS). In Excel haben Sie die Möglichkeit zu wählen, ob Sie die „normale“ (VAR.P) oder die „korrigierte“ (VAR.S) Varianz berechnen wollen. Bei der Formel für die erwartungstreue Varianzschätzung kann übrigens auch ein „n“ gekürzt werden. Hierdurch erhält man die Formel für die korrigierte Varianz:

Schauen wir uns das einmal für unser Bild-Beispiel an:
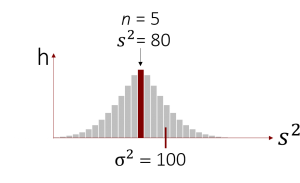
Nehmen wir an, dass wir eine Stichprobe von 5 Personen gezogen haben, die eine Varianz von s2 = 80 besitzt. Wir möchten nun anhand unserer Stichprobe die Populationsvarianz schätzen (zur Erinnerung: diese liegt bei 100). Hierzu korrigieren wir unsere Stichprobenvarianz und machen sie so zu einem erwartungstreuen Schätzer:
![]()
Unsere Punktschätzung für die Populationsvarianz ist = 100. (Und siehe da, wir haben den Populationsparameter in diesem Fall sogar richtig geschätzt)
Dieselbe Korrektur muss auch bei der Standardabweichung durchgeführt werden. Auch sie ist, wie die Stichprobenvarianz, kein erwartungstreuer Schätzer für den entsprechenden Populationsparameter. Jedoch ist diese Korrektur ein wenig aufwändiger, da wir die Standardabweichung zunächst quadrieren, um die Stichprobenvarianz zu erhalten. Zum Schluss müssen wir diesen Schritt wieder rückgängig machen und ziehen aus diesem Grund nach der Korrektur die Wurzel aus dem Ergebnis.
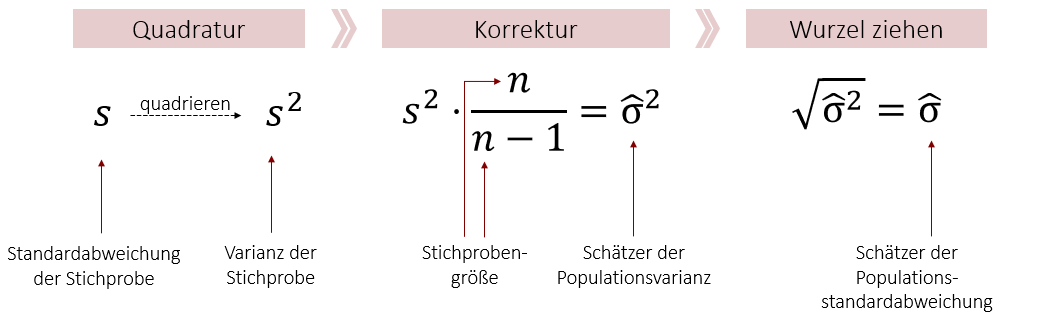
Schauen wir uns dies nochmal anhand des selben Beispiels an:
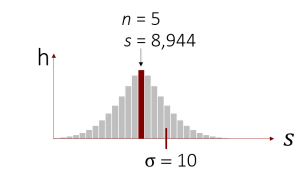
Nehmen wir an, dass wir eine Stichprobe von 5 Personen gezogen haben, die eine Standardabweichung von s = 8,944 besitzt. Wir möchten nun anhand unserer Stichprobe die Populationsstandardabweichung schätzen (zur Erinnerung: diese liegt bei 10). Hierzu korrigieren wir unsere Standardabweichung aus der Stichprobe und machen sie so zu einem erwartungstreuen Schätzer:

Nun lautet unsere Punktschätzung für die Standardabweichung der Population = 10. (Und siehe da, wir haben den Populationsparameter in diesem Fall wieder richtig geschätzt).
Übersicht
Bis auf die Varianz und die Standardabweichung sind alle gängigen Stichprobenkennwerte erwartungstreu. Das heißt, dass sie keiner Korrektur bedürfen. Die folgende Tabelle zeigt zusammenfassend, welche Stichprobenkennwerte erwartungstreu sind und welche nicht:

Expertenwissen
Bei symmetrischen Verteilungen ist der Median ebenfalls erwartungstreu und bei symmetrischen, unimodalen Verteilungen auch der Modus. Allerdings ist hier der Standardfehler (was dies genau ist, erfahren Sie im nächsten Abschnitt) größer. Daher ist der Mittelwert der effizientere Schätzer.
Sind noch Fragen offen geblieben? Das folgende Video veranschaulicht Ihnen die Thematik anhand eines Beispiels der Burgerkette Five Profs.
8.3 Parameterschätzung | Erwartungstreue Schätzer
8.5 Effizienz von (erwartungstreuen) Schätzern
Mit einem erwartungstreuen Schätzer wissen wir lediglich, dass unsere Punktschätzung nicht systematisch verzerrt ist und damit beispielsweise zu niedrig schätzt. Wir wissen jedoch nichts darüber, wie gut bzw. schlecht unsere Schätzung ist. Um dies herauszufinden, sollten wir eine weitere Eigenschaft unserer Schätzer betrachten – ihre Genauigkeit. Diese Genauigkeit wird auch als Effizienz von Schätzern bezeichnet. Ein Schätzer gilt dabei als effizient, wenn er im Vergleich zu anderen Schätzern genauer schätzt.
Um die Effizienz eines Schätzers zu verdeutlichen, lohnt sich ein Blick auf die Stichprobenkennwerteverteilung eines effizienten und eines nicht effizienten Schätzers:
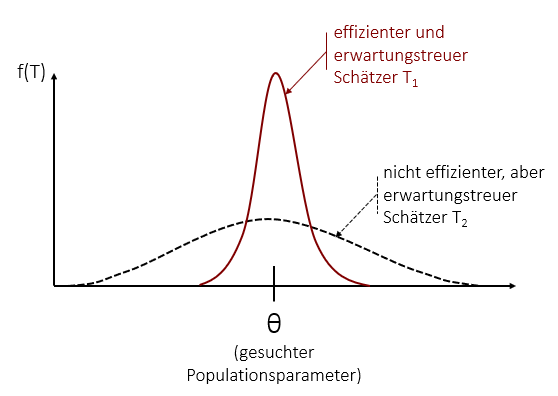
Wir sehen, dass der effiziente Schätzer T1 eine kleinere Varianz aufweist. Durch seine geringere Streuung weicht er weniger vom gesuchten Parameter ab und trifft somit bei seinen Schätzungen öfters ins Schwarze als T2. Um also die Genauigkeit einer Punktschätzung zu bestimmen, gibt man die Streuung, bzw. genauer gesagt die Standardabweichung, des Schätzers an. Man bezeichnet sie auch als Standardfehler oder, wenn man korrekt sein möchte: Standardfehler des Schätzers des Kennwerts.
8.6 Standardschätzfehler
Der Standardfehler eines Kennwerts entspricht der Standardabweichung der Stichprobenkennwerteverteilung. Über den Standardfehler kann man bestimmen, mit welcher Genauigkeit man von einem Stichprobenkennwert auf den Populationsparameter schließen kann. Je kleiner dabei der Standardfehler ist, umso genauer kann man – ausgehend von dem Kennwert einer Stichprobe – den zugehörigen Populationsparameter schätzen. Graphisch kann man dies gut in unserer Stichprobenkennwerteverteilung sehen. Der effiziente und damit genauere Schätzer T1 hat einen deutlich kleineren Standardfehler als Schätzer T2:
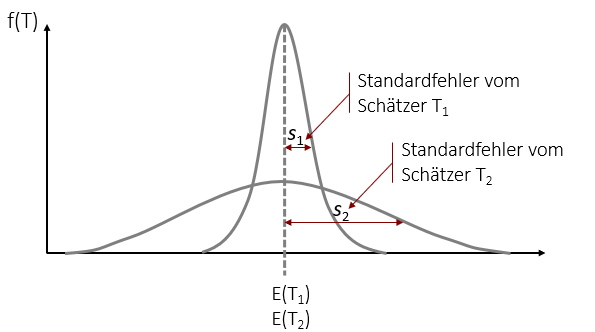
Je nach Kennwert (Mittelwert, Standardabweichung) gibt es einen anderen Standardfehler. Beispielsweise den Standardfehler des Schätzers des Mittelwerts oder den Standardfehler des Schätzers der Varianz.
Im Folgenden behandeln wir beispielhaft den Standardfehler des Mittelwerts, der über eine Zufallsstichprobe geschätzt worden ist. Er ist der wichtigste und geläufigste aller Standardfehler. Die anderen Standardfehler gehören zum Expertenwissen und kommen deshalb am Ende des Kapitels noch einmal vor.
Der Standardfehler des Schätzers des Mittelwerts wird von zwei verschiedenen Variablen beeinflusst: von der Populationsvarianz und der gewählten Stichprobengröße. Beide Faktoren haben wir bereits im Kapitel „Stichprobenkennwerteverteilung“ behandelt, jedoch werden wir sie noch einmal kurz wiederholen, um die spätere Berechnung verständlicher zu machen. Der Standardfehler des Mittelwertes wird beeinflusst durch:
- Die Stichprobengröße
Die Form und die Streuung der Stichprobenkennwerteverteilung von verändert sich mit steigender oder sinkender Stichprobengröße. Je größer dabei die Stichprobe, desto kleiner ist der Standardfehler der Stichprobenkennwerteverteilung. Warum ist dies so? Kleinere Stichproben (z.B. n = 3) neigen schnell zu „extremen“ Mittelwerten, da diese von einzelnen Datenpunkten (und damit auch Ausreißern) stark beeinflusst werden. Dadurch streut ihre Stichprobenkennwerteverteilung deutlich stärker als bei größeren Stichproben (z.B. n = 100). Hier mitteln sich die Daten schneller aus, sodass extreme Mittelwerte eher selten sind und die Stichprobenkennwerteverteilung somit eine geringere Varianz besitzt.

- Die Populationsvarianz
Der Standardfehler von verändert sich proportional zur Streuung des Merkmals in der Population. Je kleiner die Streuung in der Population, desto kleiner ist der Standardfehler und desto kleiner der Standardfehler, desto wahrscheinlicher haben wir eine genaue Schätzung. Warum ist das so? Wenn wir grundsätzlich eine sehr homogene Population haben, dann sind auch die Stichproben, die wir aus ihr gewinnen, viel homogener, als wenn die Population stark streut. Erinnern Sie sich an das Beispiel mit den Lieblingseissorten bei Kindern und Erwachsenen? Erwachsene bilden in Bezug auf Anzahl der Lieblingseissorten eine relativ homogene Population. Bei den Kindern hingegen ist die Streuung in der Population viel größer.

Wenn wir also den Standardfehler von berechnen möchten, dürfen wir diese zwei Variablen nicht außer Acht lassen. Aus diesem Grund sind sie fester Bestandteil der Berechnungsformel, die nur exakt diese beiden Faktoren beinhaltet.
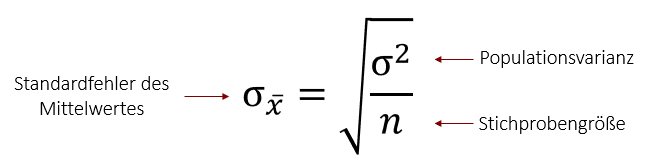
Das Problem an dieser Berechnungsformel ist, dass wir oftmals nur eine Stichprobe ziehen und somit die Populationsvarianz nicht kennen. Aus diesem Grund müssen wir den Standardfehler des Mittelwertes schätzen und zwar auf Basis der Varianz unserer gezogenen Stichprobe.
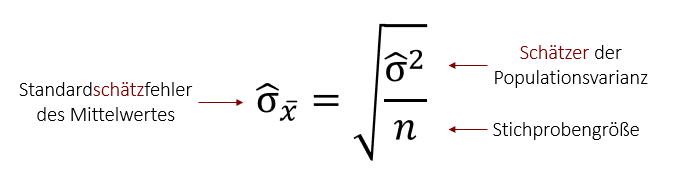
Unser Standardfehler wird somit zum Standardschätzfehler bzw. zum Standardfehler des Schätzers. In der Formel bekommt der Standardfehler aus diesem Grund ein „Dach“. So sehen wir, dass es sich nur um eine Schätzung handelt. Dadurch können wir statt der Populationsvarianz eine Schätzung der Populationsvarianz in die Formel eintragen. Wer sich an das letzte Kapitel erinnert, weiß, dass wir für diese Schätzung jedoch nicht einfach die Stichprobenvarianz nehmen können. Sie ist kein erwartungstreuer Schätzer und muss deshalb zunächst korrigiert werden, bevor wir sie als Schätzer der Populationsvarianz in die Formel einsetzen können.
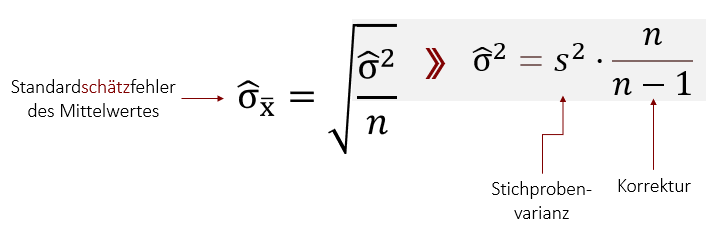
Lassen Sie uns das noch einmal anhand eines Beispiels durchgehen:
Beispiel
An einer repräsentativen Stichprobe von 100 Personen wird ein Test zur Ermittlung der Koordinationsfähigkeit durchgeführt. Die Testleistungen haben einen Mittelwert von = 80 und eine Varianz von s2 = 396.
Wie hoch ist der Standardfehler des Schätzers des Mittelwerts?
- Berechnung des Schätzers der Populationsvarianz
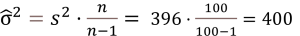
- Berechnung des Standardschätzfehlers
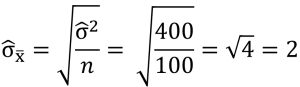
Der Standardschätzfehler des Mittelwerts ist = 2. Wenn wir also eine Punktschätzung des Populationsmittelwerts machen, so liegt die durchschnittliche Koordinationsfähigkeit der Population bei 80 (Punktschätzung) und der Standardfehler des Schätzers bei plus minus 2. Dieses Gütemaß gibt an, dass wir uns im „Mittel“ um 2 Einheiten irren.
Expertenwissen
Der Standardfehler existiert nicht nur für den Mittelwert, sondern kann für jeden Kennwert berechnet werden, wenn man von einer Zufallsstichprobe ausgeht. Hier einige Beispiele für Standardschätzfehler:

Noch Fragen offen geblieben? Das folgende Video erklärt Ihnen den Standardschätzfehler anhand eines Beispiels aus der Burgerkette Five Profs.
8.5 Parameterschätzung | Standardfehler
Für weitere Rechenbeispiele und zum besseren Verständnis der Berechnungsformel zeigt Ihnen das folgende Video noch mehr Beispiele aus der Five Profs Kette.
8.6 Parameterschätzung | Standardfehler Rechenbeispiele
8.7 Fazit Punktschätzung
Die Punktschätzung erlaubt uns auf Basis von Stichprobenkennwerten einen unbekannten Populationsparameter zu schätzen. In diesem Kapitel haben wir gelernt, dass wir zur Punktschätzung erwartungstreue Schätzer heranziehen müssen und die Genauigkeit der Schätzung durch den Standardschätzfehler bestimmen können.
Letztendlich gaukelt uns dieses Verfahren jedoch eine „Pseudogenauigkeit“ vor: Wir geben den geschätzten Parameterwert punktgenau an und das, obwohl wir den wahren Parameterwert sehr selten exakt treffen werden. Man kann also eine Punktschätzung mit dem Versuch vergleichen, eine winzige Fliege (den wahren Parameterwert) mit einer Stecknadel (dem Punktschätzer) zu treffen. Der erfahrene Fliegenjäger würde der Stecknadel eine Fliegenklatsche vorziehen. In der Statistik wäre ein Intervall die Entsprechung, was uns zum nächsten Kapitel dieses Buches führt – der Intervallschätzung.
8.8 Übungsfragen
Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!
In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!
8.9 Übungsaufgaben




