Hypothesentests
10 Hypothesentest/Signifikanztest
10.0 Einführung Hypothesentest
Hypothesen sind Behauptungen über die Wirklichkeit (in der Population), die über den bisherigen Erkenntnisstand hinausgehen. Im Privatleben stellen wir täglich neue Hypothesen auf, auch wenn wir uns darüber meist nicht bewusst sind.
Einfache Beispiele für Hypothesen
- Tägliches Fahrradfahren macht glücklich
- Frauen sind öfter auf sozialen Medien als Männer
- Das Einkommen beeinflusst die Arbeitnehmerzufriedenheit
Aus wissenschaftlicher Sicht sollte eine gute Hypothese provozierende, jeweils nicht triviale Vorhersagen ermöglichen. Man spricht hierbei von Hypothesen mit hohem empirischem Gehalt, da sie besonders viele neue Erkenntnisse durch die Beobachtung ermöglichen. Hypothesen sollten grundsätzlich auch widerlegbar sein. Theorien, die grundsätzlich stimmen (sog. Tautologien ) sind keine Hypothesen. Die Bauernregel „Wenn der Hahn kräht auf dem Mist, ändert sich das Wetter, oder es bleibt, wie es ist“ eignet sich daher nicht als Hypothese. In Summe ergeben sich hieraus vier wesentliche Anforderungen an wissenschaftliche Hypothesen. Diese lauten:
- Präzise und widerspruchsfreie Formulierung
- Widerlegbarkeit (Negativ-Beispiel: Wenn der Hahn kräht auf dem Mist, ändert sich das Wetter oder es bleibt, wie es ist)
- Operationalisierbarkeit: Es muss klar sein, wie man die Variablen einer Hypothese messen kann und diese Operationalisierung muss die Gütekriterien Objektivität, Reliabilität und Validität erfüllen.
- Begründbarkeit: Die Hypothese sollte entweder auf Basis von bestehenden Studien oder Theorien oder auf Basis von Vorstudien oder eigenen Beobachtungen bzw. Überlegungen aufgestellt werden.
Video 10.2 Hypothesentest Signifikanztest | Hypothesen
10.1 Alternativ- und Nullhypothese
10.2 Falsifikationsprinzip
Eine Person geht öfter an Gewässern spazieren und beobachtet Schwäne. Diese sind alle weiß, daher schließt die Person vom Besonderen (ihrer Beobachtung) auf die allgemeine These: Alle Schwäne sind weiß. Die Frage hierbei ist, ab wie vielen Beobachtungen von weißen Schwänen die Person mit Sicherheit sagen kann, dass alle Schwäne weiß sind. Hierauf kann man keine Antwort geben, denn jeder weitere weiße Schwan bringt nur wenig Erkenntnisgewinn. Jedoch reicht nur ein einziger schwarzer Schwan, um die Theorie zu widerlegen. Daher ist der empirische Gehalt des einen schwarzen Schwans deutlich höher. Anstatt nach weiteren weißen Schwänen zu suchen, ist es daher sinnvoller, nach schwarzen (oder andersfarbigen) Schwänen zu suchen. Bleibt dies erfolglos, so kann daraus geschlossen werden, dass wohl alle Schwäne weiß sind – dies ist das Falsifikationsprinzip. Daher werden wir im Folgenden bei allen Arten von Hypothesen-Tests immer das Ziel verfolgen die Nullhypothese (also das Gegenteil von dem, was wir eigentlich als These aufstellen) zu widerlegen. Sollte uns das gelingen, nehmen wir an, dass unsere ursprüngliche These (Alternativhypothese) wahr ist. Dieses „um die Ecke denken“ fällt jedoch in der Praxis nicht nur den Einsteigern in der Statistik schwer. Daher ist das Prinzip der Nullhypothesen-Signifikanztests immer wieder in der Kritik.
Video 10.3 Hypothesentest Signifikanztest | Falsifikationsprinzip Nullhypothese und Alternativhypothese
10.3 Arten von Hypothesen
Wie Sie in den Beispielen am Anfang dieses Kapitels schon gesehen haben, gibt es sehr unterschiedliche Arten von Hypothesen. Grundsätzlich lassen sich Hypothesen in Zusammenhangs- und Unterschiedshypothesen einteilen. Unterschiedshypothesen erlauben den Vergleich von zwei (oder mehr) Gruppen von Merkmalsträgern, hinsichtlich einer abhängigen Variable. Beispielsweise lautet eine Unterschiedshypothese: „Unterscheiden sich Männer und Frauen bei der Klausurnote in Statistik?“. Zusammenhangshypothesen erlauben eine Aussage über Art und Intensität des Zusammenhangs von 2 Variablen. Beispielsweise lautet eine Zusammenhangshypothese: „Gibt es einen Zusammenhang zwischen Schlafdauer und Klausurnote?“. Grundsätzlich lassen sich Zusammenhangshypothesen in Unterschiedshypothesen umwandeln und umgekehrt. Welche Art von Hypothese besser geeignet ist, hängt dabei vom Studiendesign ab. Betrachten Sie z.B. zwei oder mehr Gruppen (z.B. Männer und Frauen), dann sind Unterschiedshypothesen passender. Betrachten Sie zwei skalierte Merkmale (Alter und Konzentrationsfähigkeit), dann sind Zusammenhangshypothesen besser geeignet. Sie sollten jedoch lernen, jede Fragestellung sowohl als Unterschieds-, als auch als Zusammenhangshypothese formulieren zu können.
Überdies können Hypothesen in gerichtete Hypothesen und ungerichtete Hypothesen aufgeteilt werden. Gerichtete Hypothesen machen Aussagen über die Richtung des erwarteten Unterschieds oder Zusammenhangs zwischen den untersuchten Kennwerten. Ungerichtete Hypothesen lassen die Richtung des Zusammenhangs bzw. Unterschieds offen. Gerichtete Hypothesen setzen mehr Vorwissen voraus und sollten daher nur eingesetzt werden, wenn es vorab zur Untersuchung schon klar ist, dass der Effekt nur in eine Richtung gehen kann (z.B. aufgrund von Vorstudien oder logischer Überlegungen).
| ungerichtet | gerichtet | |
| Zusammen- hang |
Es gibt einen Zusammen- hang zwischen Schlafdauer und Klausurnote |
Es gibt einen positiven Zusammen- hang zwischen Schlafdauer und Klausurnote |
| Unterschied | Männer und Frauen sind im Mittel unterschiedlich gut in Statistik | Männer sind im Mittel besser in Statistik als Frauen |
Gerichtete Hypothesen können weiter unterschieden werden in spezifische und unspezifische Hypothesen. Spezifische Hypothesen machen Aussagen über die Größe (= | < | >) des erwarteten Unterschieds oder Zusammenhangs zwischen den untersuchten Kennwerten. Diese setzen daher noch mehr Vorwissen voraus.
| unspezifisch | spezifisch | |
| Zusammen- hang |
Es gibt einen positiven Zusammen- hang zwischen Schlafdauer und Klausurnote |
Die Korrelation zwischen Schlaf- dauer und Klausurnote beträgt r ≥.30 |
| Unterschied | Männer schneiden in der Statistikklausur im Mittel besser ab als Frauen | Männer schneiden in der Statistik- klausur im Mittel eine ganze Note besser ab als Frauen |
10.4 Hypothesen aufstellen
Für die Durchführung von empirischen Studien müssen Forschungs-Hypothesen zunächst operationalisiert werden. Die operationale Hypothese ergänzt die Forschungs-Hypothese unter der Angabe, wie die einzelnen Konstrukte gemessen bzw. operationalisiert werden. Wenn zum Beispiel die Hypothese aufgestellt wird, dass Wasser trinken gesund macht, so muss in diesem Schritt entschieden werden, mit welcher messbaren Variable das Konstrukt „Gesund“ gemessen wird. Im nächsten Schritt müssen die Hypothesen dann in statistische Hypothesen „übersetzt“ werden. Die statistische Hypothese formuliert zugehörige Erwartungen der Hypothese an Populationsparameter. Beispielsweise könnte hierbei die Hypothese spezifiziert werden, dass ein mindestens schwacher negativer Zusammenhang (r < .1) zwischen dem Wasserkonsum pro Tag und den Krankheitstagen erwartet wird. Diese statistischen Hypothesen können dann mittels statistischer Tests geprüft werden. Daraus lässt sich dann am Ende ableiten, ob eine Forschungshypothese beibehalten werden soll oder nicht.
Beispiel Operationalisierung von Hypothesen
Forschungs-Hypothese: Wasser trinken ist gesund
Operationale Hypothese: Je mehr Liter Wasser eine Person pro Tag trinkt, umso weniger Krankheitstage hat eine Person im Jahr
Statistische Hypothese: Negative Korrelation (r < .1) zwischen Wassermenge und Krankheitstagen
| ungerichtet | gerichtet | |
| Zusammen- hang |
Es gibt einen Zusammen- hang zwischen Schlafdauer und KlausurnoteH0: ρ = 0H1: ρ ≠ 0 |
Schlafdauer und Klausurnote sind positiv korreliert
H0: ρ ≤ 0 H1: ρ > 0 |
| Unterschied | Männer und Frauen sind unterschiedlich gut in Statistik
H0: μMänner = μFrauen H1: μMänner ≠ μFrauen |
Männer sind besser in Statistik als Frauen
H0: μMänner ≤μFrauen H1: μMänner > μFrauen |
Video 10.4 Hypothesentest Signifikanztest | Hypothesen aufstellen
10.5 Der Signifikanztest
Bei der hypothesengeleiteten Forschung stellen wir Behauptungen (Hypothesen) über die Wirklichkeit (Population) auf und prüfen, in wieweit diese durch die Daten einer Stichprobe bestätigt werden können. In der Inferenzstatistik gehen wir dabei immer davon aus, dass es sich um reine Zufallsstichproben handelt. Diese sind zufällig aus der Population gezogen und daher verändert sich auch deren Zusammensetzung mit jedem „ziehen“ aus der Population. Doch wie kann ich nun Annahmen über die Population anhand einer Stichprobe prüfen, wenn die Kennwerte (z.B. Mittelwert) von Stichprobe zu Stichprobe zufällig schwanken? Genau hier hilft die Inferenzstatistik weiter, indem sie Entscheidungsregeln definiert, wann eine Hypothese beibehalten oder verworfen wird. Diese Regeln legen fest, wann ein Ereignis (z.B. eine Abweichung des Mittelwerts) als zu unwahrscheinlich eingestuft wird, um nur durch eine zufällige Schwankung aufgetreten zu sein. Diese Entscheidungsregeln nennt man Signifikanztest. Der Signifikanztest prüft, wie gut bzw. mit welcher Wahrscheinlichkeit die gefundenen Daten zur postulierten Hypothese passen.
Beispiel Signifikanztest
Ein Professor möchte herausfinden, ob YouTube Lernvideos die Klausurnote verbessern. Da die Klausuren immer gleich aufgebaut sind, weiß er, dass der langjährig gemessene Mittelwert der erreichten Punkte in der Klausur bei μ= 67 (von 100) liegt. Er wählt zufällig n= 30 Studenten aus, die exklusiv Zugang zu neuen YouTube Lernvideos bekommen. Nach der Klausur berechnet er den Mittelwert dieser Stichprobe und erhält ![]() = 71 Punkte.
= 71 Punkte.
Die Studenten mit Zugang zu den YouTube Videos haben nun also im Mittel um 4 Punkte besser abgeschnitten als der langjährige Durchschnitt der Studierenden. Aber woran kann das liegen? Hierfür gibt es zwei mögliche Erklärungen:
Option A:
Die YouTube Videos funktionieren und die Studierenden konnten dadurch wirklich besser lernen und haben deshalb mehr Punkte in der Klausur erreicht
Option B:
Die YouTube Videos funktionieren nicht und der Effekt, den wir beobachten (+4 Punkte), ist nur durch Zufall zustande gekommen. Denn jedes Mal, wenn ich eine Zufallsstichprobe ziehe, weicht der gefundene Mittelwert ja etwas vom „wahren“ Mittelwert der Population ab.
10.6 Das Signifikanzniveau
Das Signifikanzniveau ist sozusagen die von uns (recht willkürlich) gesetzte Grenze, ab der wir noch an die H0 glauben, bzw. diese ablehnen. Die Einführung zum Signifikanzniveau wollen wir mit einer Geschichte aus dem viktorianischen England beginnen. Dort war es eine mitunter sehr emotionale Diskussion, ob zuerst Milch oder zuerst Tee in eine Tasse gegossen werden sollte. Der Statistiker Ronald Fisher erzählte hierzu 1919 die (wohl wahre) Geschichte von Muriel Bristol, die hier stark vereinfacht wiedergegeben ist. Die Dame behauptete am Geschmack eines Tees feststellen zu können, welche Flüssigkeit zuerst eingegossen wurde. Er fragte sich, wie viele Tassen Tee die Dame richtig raten müsse, damit man ihr glauben kann.[2]
Wann würden Sie ihr glauben? Wenn Sie korrekt liegt bei..
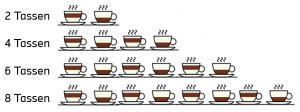
Die meisten Personen antworten auf diese Frage intuitiv, dass sie Frau Bristol ab vier in Folge richtig geratenen Tassen glauben würden. Die skeptischeren Personen ab sechs oder gar erst ab acht Tassen. Doch wie können wir uns dieser Frage nun wissenschaftlich nähern? Wenn Frau Bristol tatsächlich keinerlei Fähigkeiten hat und nur blind raten würde, dann ist die Wahrscheinlichkeit vier Tassen korrekt zu raten 6,3% (Bei jeder Tasse liegt die Wahrscheinlichkeit richtig zu liegen bei 50%, daher 0,54 = 0,063). Die Wahrscheinlichkeit, sechs Tassen korrekt zu raten, liegt bei 1,6% ( berechnet mit 0,56). Scheinbar sagt uns also unsere „Intuition“, dass wir bei einer Wahrscheinlichkeit kleiner 6 Prozent oder kleiner 1,6 Prozent nicht mehr an einen Zufall glauben sollten. Wo diese Grenze liegt, das dürfen tatsächlich immer Sie als Forschende festlegen. Tatsächlich sind diese „intuitiven“ Grenzen aber sehr nahe an den wissenschaftlichen Standards, die sich gemeinhin durchgesetzt haben. Per Konvention finden in der Forschung folgende Signifikanzniveaus Anwendung:
| α | % | Beschreibung |
| α = 0,1 (.10) | 10% Signifikanzniveau | marginal signifikant |
| α = 0,05 (.05) | 5% Signifikanzniveau | signifikant |
| α = 0,01 (.01) | 1% Signifikanzniveau | hoch signifikant |
| α = 0,001 (.001) | 0,1% Signifikanzniveau | höchst signifikant |
Grundsätzlich sollte man das Signifikanzniveau an den jeweiligen Forschungsgegenstand anpassen. Ein α-Fehler von 5% ist in vielen Studien durchaus akzeptabel, wenn es z.B. um die Entwicklung eines neuen Burger-Konzeptes geht. Für die Diagnose einer lebensbedrohlichen Krankheit wäre dies jedoch sicherlich inakzeptabel.
Expertenwissen α und β-Fehler
Neben dem α-Fehler (auch Type I-Error oder ‚False Positive‘) existiert auch der sogenannte β-Fehler (Type II-Error oder ‚False Negative‘). Dieser in der Praxis oft wenig beachtete Fehler drückt aus, wie sensitiv mein Test ist. Der übliche akzeptierte β-Fehler liegt in der Wissenschaft bei rund 20% und damit deutlich höher als der tolerierte α-Fehler. Je nach Forschungsgegenstand kann der β-Fehler jedoch sehr bedeutsam sein. Wenn es beispielsweise darum geht, eine Schwangerschaft zu diagnostizieren, wie im unten stehenden Beispiel, würden wir wohl eine Fehlerrate von 20% nicht akzeptieren.
| Realität | ||
| Studien- ergebnisse: |
Kein Signifikanter Effekt | Signifikanter Effekt |
| Kein Signifikanter Effekt | Richtig | β-Fehler |
| Signifikanter Effekt | α-Fehler | Richtig |
Am Beispiel eines Schwangerschaftstests:
| Realität | ||
| Studien- ergebnisse: |
Kein Signifikanter Effekt | Signifikanter Effekt |
| Kein Signifikanter Effekt | Korrekte Diagnose | Schwangere Frau nicht als schwanger erkannt |
| Signifikanter Effekt | Frau die nicht schwanger ist als schwanger erkannt | Korrekte Diagnose |
Doch wie kommen wir nun zur Entscheidung über die Hypothesen? Hierzu wollen wir uns im folgenden Kapitel dem ersten Signifikanztest widmen, dem sogenannten Z-Test oder Gauß-Test.
10.7 Übungsfragen
Bei den folgenden Aufgaben können Sie Ihr theoretisches Verständnis unter Beweis stellen. Auf den Karteikarten sind jeweils auf der Vorderseite die Frage und auf der Rückseite die Antwort dargestellt. Viel Erfolg bei der Bearbeitung!
In diesem Teil sollen verschiedene Aussagen auf ihren Wahrheitsgehalt geprüft werden. In Form von Multiple Choice Aufgaben soll für jede Aussage geprüft werden, ob diese stimmt oder nicht. Wenn die Aussage richtig ist, klicke auf das Quadrat am Anfang der jeweiligen Aussage. Viel Erfolg!


